Cholesky decomposition, locality

Primary author of this description: Vadim Voevodin (Section 2).

1 Links

The main fragment of the implementation used to obtain the quantitative estimates is given here (the Kernel function).

2 Locality of data and computations

2.1 Locality of implementation

The startup conditions are discussed here.

2.1.1 Structure of memory access and a qualitative estimation of locality

Figure 1. Implementation of the Cholesky algorithm. A general memory-access profile.

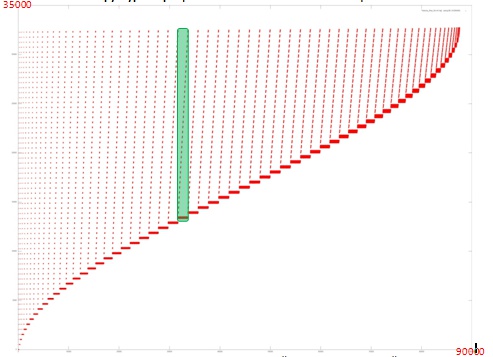
A memory access profile is illustrated in Fig. 1 for an implementation of the Cholesky algorithm with a single working array. In this profile, hence, only the elements of this array are referenced. The above-illustrated implementation consists of a single main stage; in its turn, this stage consists of a sequence of similar iterations. An example of such an iteration is highlighted in green.

From Fig.1 it follows that, at each [math]i[/math]th iteration, all the addresses starting with a certain one are being used and the address of the first processed element increases with increasing [math]i[/math]. We should also note that, at each iteration, the number of memory accesses increases up to the middle of the algorithm; after that, this number decreases down to the end of the algorithm. This fact allows us to conclude that the data processed by the algorithm are used nonuniformly and that many iterations (especially at the beginning of the process) use a large amount of data, which decreases the memory access locality.

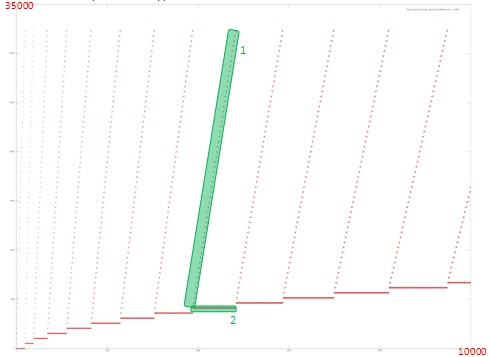
In this case, however, the structure of iterations is the main factor influencing the memory access locality. Fig.2 illustrates a fragment of the memory access profile for several first iterations.

Figure 2. Implementation of the Cholesky algorithm. A profile fragment (several first iterations).

From Fig.2 it follows that each iteration consists of two different fragments. The first fragment is the serial access to the addresses starting with a certain initial address; each element of the working array is rarely referenced. This fragment possesses a good spatial locality, since the step in memory between the adjacent memory references is not large; however, its temporal locality is bad, since the data are rarely reused.

The locality of the second fragment is much better, since a large number of references are made to the same data, which ensures a large degree of spatial and temporal locality than that of the first fragment.

We can also estimate the overall locality of these two fragments for each iteration. However, it is reasonable to consider the structure of each fragment in more detail.

Figure 3. Implementation of the Cholesky algorithm. A profile fragment (a part of a single iteration).

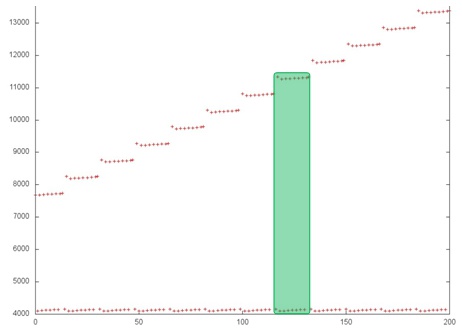
Fig.3 illustrates a part of a single iteration and shows that the structure of the above two fragments is more complicated than it can be concluded from Fig.2. In particular, each step of fragment 1 consists of several references to adjacent addresses and the memory access is not serial. Fragment 2 consists of repetitive iterations; each step of fragment 1 corresponds to a single iteration of fragment 2 (highlighted in green in Fig.3). This fact indicates that, in order to exactly understand the local profile structure, it is necessary to consider this profile on the level of individual references.

It should be noted that the conclusions made on the basis of Fig.3 supplement the general knowledge on the structure of the memory access profile, whereas the conclusions on the locality of the above two fragments made on the basis of Fig.2 remain valid.

2.1.2 Quantitative estimation of locality

The first estimate is made on the basis of the daps characteristic used to evaluate the number of write and read operations per second. This characteristic is similar to the flops estimate for memory access and is an estimate of the memory usage performance rather than an estimate of locality. However, the daps characteristic is a good information source and can be used to compare with the results obtained according to the cvg characteristic.

Figure 4. Comparison of daps values.

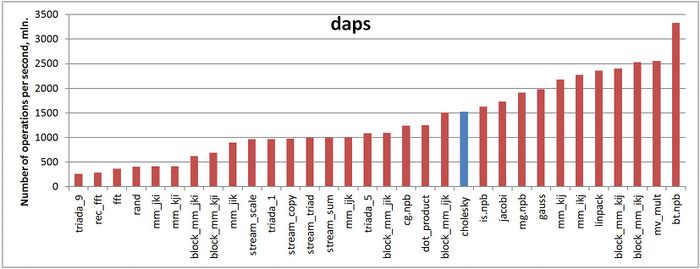
Fig.4 illustrates the daps characteristics for a number of implementations of some widespread algorithms. The values of this characteristic are given in increasing order: a higher performance level corresponds to a larger value of daps. From this figure it follows that the Cholesky algorithm is characterized by a sufficiently large rate of memory usage; however, this rate is lower than that of the LINPACK test or the Jacobi method.

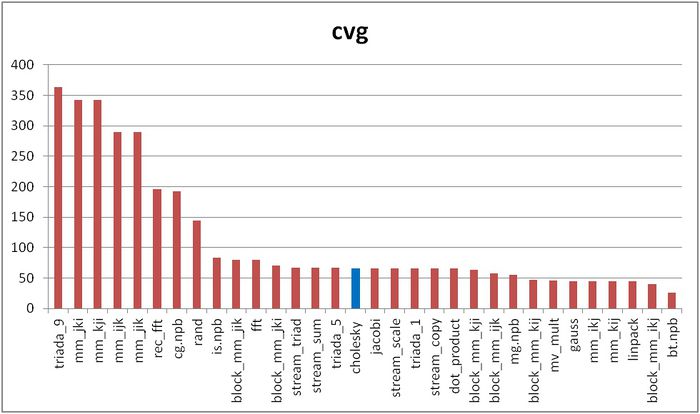
The cvg characteristic is used to obtain a more machine-independent estimate of locality and to specify the frequency of fetching data to the cache memory. A lesser value of cvg corresponds to a higher level of locality and to a smaller number of the above fetching procedure.

Figure 5. Comparison of cvg values.

Fig.5 shows the cvg values for the same implementations presented in Fig.4. These values are given in decreasing order: the higher locality level corresponds to a smaller cvg value. From this figure it follows that the Cholesky algorithm occupies a lower position than it has in the performance list given in Fig.4 for the daps characteristic.