Boruvka's algorithm

Алгоритм Борувки
Sequential algorithm
Serial complexity	[math]O(|E|ln(|V|))[/math]
Input data	[math]O(|V| + |E|)[/math]
Output data	[math]O(|V|)[/math]
Parallel algorithm
Parallel form height	[math]max O(ln(|V|)) [/math]
Parallel form width	[math]O(|E|)[/math]

1 Properties and structure of the algorithm

1.1 General description of the algorithm

The Borůvka algorithm was designed for constructing the minimum spanning tree in a weighted undirected graph. It is well parallelizable and is a foundation of the distributed GHS algorithm.

1.2 Mathematical description of the algorithm

Let [math]G = (V, E)[/math] be a connected undirected graph with the edge weights [math]f(e)[/math]. It is assumed that all the edges have distinct weights (otherwise, the edges can be sorted first by weight and then by index).

The Borůvka's algorithm is based on the following two facts:

• Minimum edge of a fragment. Let [math]F[/math] be a fragment of the minimum spanning tree, and let [math]e_F[/math] be an edge with the least weight outgoing from [math]F[/math] (that is, exactly one of its ends is a vertex in [math]F[/math]). If such an edge [math]e_F[/math] is unique, then it belongs to the minimum spanning tree.
• Merging fragments. Let [math]F[/math] be a fragment of the minimum spanning tree of [math]G[/math], while the graph [math]G'[/math] is obtained from [math]G[/math] by merging the vertices that belong to [math]F[/math]. Then the union of [math]F[/math] and the minimum spanning tree of [math]G'[/math] yields the minimum spanning tree of the original graph [math]G[/math].

At the start of the algorithm, each vertex of [math]G[/math] is a separate fragment. At the current step, the outgoing edge with the least weight (if such an edge exists) is chosen for each fragment. The chosen edges are added to the minimum spanning tree, and the corresponding fragments are merged.

1.3 Computational kernel of the algorithm

The basic operations of the algorithm are:

1. Search for the outgoing edge with the least weight in each fragment.
2. Merging fragments.

1.4 Macro structure of the algorithm

For a given connected undirected graph, the problem is to find the tree that connects all the vertices and has the minimum total weight.

The classical example (taken from Borůvka's paper) is to design the cheapest electrical network if the price for each piece of electric line is known.

Let [math]G=(V,E)[/math] be a connected graph with the vertices [math]V = ( v_{1}, v_{2}, ..., v_{n} )[/math] and the edges [math]E = ( e_{1}, e_{2}, ..., e_{m} )[/math]. Each edge [math]e \in E[/math] is assigned the weight [math]w(e)[/math].

It is required to construct the tree [math]T^* \subseteq E[/math] that connects all the vertices and has the least possible weight among all such trees:

[math] w(T^* )= \min_T( w(T)) [/math].

The weight of a set of edges is the sum of their weights:

[math]w(T)=\sum_{e \in T} (w(T))[/math]

If [math]G[/math] is not connected, then there is no tree connecting all of its vertices.

In this case, it is required to find the minimum spanning tree for each connected component of [math]G[/math]. The collection of such trees is called the minimum spanning forest (abbreviated as MSF).

1.4.1 Auxiliary algorithm: system of disjoint sets (Union-Find)

Every algorithm for solving this problem must be able to decide which of the already constructed fragments contains a given vertex of the graph. To this end, the data structure called a «system of disjoint sets» (Union-Find) is used. This structure supports the following two operations:

1. [math]FIND(v) = w[/math] – for a given vertex v, returns the vertex w, which is the root of the fragment that contains v. It is guaranteed that u and v belong to the same fragment if and only if [math]FIND(u) = FIND(v)[/math].

2. [math]MERGE(u, v)[/math] – combines two fragments that contain the vertices [math]u[/math] and [math]v.[/math] (If these vertices already belong to the same fragment, then nothing happens.) It is convenient that, in a practical implementation, this operation would return the value "true" if the fragments were combined and the value "false," otherwise.

1.4.2 Последовательная версия

The classical serial algorithm Union-Find is described in a Tarjan's paper. Each vertex v is assigned the indicator to the parent vertex [math]parent(v)[/math].

1. At first, [math]parent(v) := v[/math] for all the vertices.

2. [math]FIND(v)[/math] is executed as follows: set [math]u := v[/math]; then follow the indicators [math]u := parent(u)[/math] until the relation [math]u = parent(u)[/math] is obtained. This is the result of the operation. An additional option is the merging of tree: for all the visited vertices, set [math]parent(u_i) := u[/math] or perform the merging operation along the way: [math]parent(u) := parent(parent(u)))[/math].

3. [math]MERGE(u, v)[/math] is executed as follows: first, find the root vertices [math]u := FIND(u), v := FIND(v)[/math]. If [math]u = v[/math], then the original vertices belong to the same fragment and no merging occurs. Otherwise, set either [math]parent(u) := v[/math] or [math]parent(v) := u[/math]. In addition, one can keep track of the number of vertices in each fragment in order to add the smaller fragment to the greater one rather than otherwise. (Complexity estimates are derived exactly for such an implementation; however, in practice, the algorithm performs well even without counting the number of vertices.)

1.5 Implementation scheme of the serial algorithm

In Borůvka's algorithm, the fragments of the minimum spanning tree are build up gradually by joining minimum edges outgoing from each fragment.

1. At the start of the algorithm, each vertex is a separate fragment.

2. At each step:

• For each fragment, the outgoing edge with the minimum weight is determined.

• Minimum edges are added to the minimum spanning tree, and the corresponding fragments are combined.

3. The algorithm terminates when only one fragment is left or no fragment has outgoing edges.

The search for minimum outgoing edges can be performed independently for each fragment. Therefore, this stage of computations can be efficiently parallelized (including the use of the mass parallelism of graphic accelerators).

The merging of fragments can also be implemented in parallel by using the parallel version of the algorithm Union-Find, which was described above.

An accurate count of the number of active fragments permits to terminate Borůvka's algorithm at one step earlier compared to the above description:

1. At the start of the algorithm, the counter of active fragments is set to zero.

2. At the stage of search for minimum edges, the counter is increased by one for each fragment that has outgoing edges.

3. At the stage of combining fragments, the counter is decreased by one each time when the operation [math]MERGE(u, v)[/math] returns the value "true".

If, at the end of an iteration, the value of the counter is 0 or 1, then the algorithm stops. Parallel processing is possible at the stage of sorting edges by weight; however, the basic part of the algorithm is serial.

1.6 Serial complexity of the algorithm

The serial complexity of Borůvka's algorithm for a graph with [math]|V|[/math] vertices and [math]|E|[/math] edges is [math]O(|E| \ln(|V|))[/math] operations.

1.7 Information graph

There are two levels of parallelism in the above description: the parallelism in the classical Borůvka's algorithm (lower level) and the parallelism in the processing of a graph that does not fit in the memory.

Lower level of parallelism: search for minimum outgoing edges can be performed independently for each fragment, which permits to efficiently parallelize (both on GPU and CPU) this stage of the process. The merging of fragments can also be executed in parallel with the use of the above algorithm Union-Find.

Upper level of parallelism: constructions of separate minimum spanning trees for each edge list can be performed in parallel. For instance, the overall list of edges can be partitioned into two parts of which one is processed on GPU, while the other is in parallel processed on CPU.

Figure 1. Information graph of the lower level of parallelism

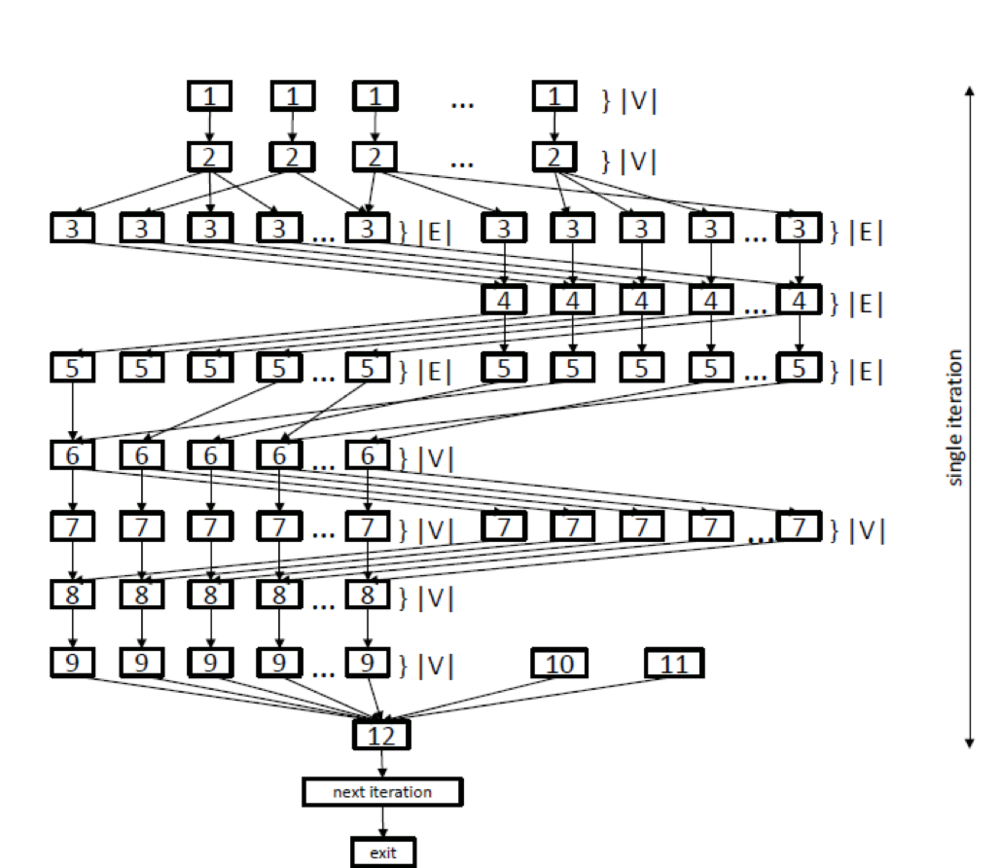
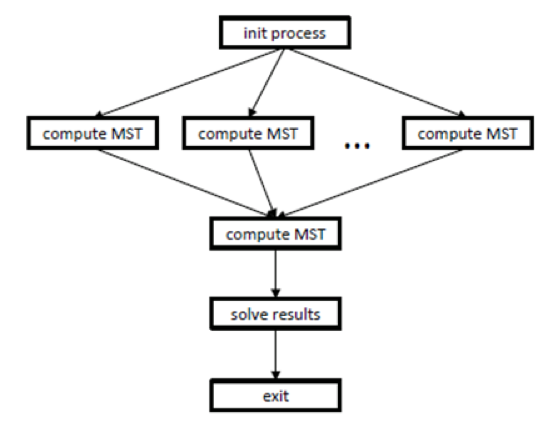
Consider the information graphs and their detailed descriptions. One can think that figure 1 shows the information graph of the classical Borůvka's algorithm, while figure 2 shows the information graph of the processing algorithm.

In the graph shown in figure 1, the lower level of parallelism is represented by levels {3, 4, 5}, which correspond to parallel search operations for minimum outgoing edges, and by levels {6, 7, 8}, which correspond to parallel operations of merging trees. Various copying operations {1, 2, 8, 9} are also performed in parallel. After the body of the loop has been executed, test {12} verifies how many trees are left at the current step. If this number was not changed, the loop terminates; otherwise, the algorithm passes to the next iteration.

As already said, the upper level of parallelism, illustrated by figure 2, refers to the parallel computation of minimum spanning trees (operation "compute mst") for different parts of the original graph. Prior to this computation, the initialization process ("init process") is performed, and its data are used by the subsequent parallel operations "compute mst". After these parallel computations, the ultimate spanning tree is calculated, and the result obtained is saved to memory ("save results").

Figure 2. Information graph of the upper level of parallelism

1.8 Parallelization resource of the algorithm

Thus, Borůvka's algorithm has two levels of parallelism.

At the upper level, the minimum spanning trees may be searched for separate parts of the list of graph edges (parallel operations "compute_MST" in figure 2). However, then the final union должно последовать финальное объединение полученных ребер и вычисление минимального остовного дерева для полученного графа, которое будет производиться последовательно.

Besides, the computation of each minimum spanning tree (parallel operations "compute_MST" in figure 2) has an intrinsic resource of parallelism discussed below. The operations of initialization and copying of data (see [1], [2], and [9] in figure 1) can be performed in parallel in [math]O(|V|)[/math] steps. The operations of searching for minimum outgoing edges (see [3],[4], and [5]) can also be executed in parallel. при том для каждой дуги и обратной к ней независимо, что даёт [math]2*O(|E|)[/math] параллельных операций. Помимо этого, операции объединения деревьев [6], [7], [8] могут так же производиться параллельно за [math]O(|V|)[/math] операций.

As a result, the width of the parallel form of the classical Borůvka's algorithm is [math]O(|E|)[/math]. The height of the parallel form depends on the number of steps in the algorithm and is bounded above by [math]O(ln(|V|))[/math].

1.9 Input and output data of the algorithm

Входные данные: взвешенный граф [math](V, E, W)[/math] ([math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] с весами [math]f_j[/math]).

Объём входных данных: [math]O(|V| + |E|)[/math].

Выходные данные: список рёбер минимального остовного дерева (для несвязного графа – список минимальных остовных деревьев для всех компонент связности).

Объём выходных данных: [math]O(|V|)[/math].

1.10 Properties of the algorithm

1. Алгоритм останавливается за конечное число шагов, поскольку на каждом шаге становится по крайней мере на один фрагмент меньше.
2. Более того, число фрагментов на каждом шаге уменьшается как минимум вдвое, так что общее число шагов составляет не более [math]\log_2 n[/math]. Отсюда следует и оценка сложности алгоритма.

2 Software implementation of the algorithm

2.2 Locality of data and computations

На этапе поиска минимального ребра происходят следующие обращения к памяти:

1. Чтение информации о рёбрах. Может производится последовательно.
2. Проверка принадлежности ребра одному и тому же фрагменту - два чтения массива [math]parent(u)[/math] с вероятным промахой по кэшу.
3. Чтение и обновление минимального веса ребра фрагмента. Данная информация может быть закеширована, особенно на поздних шагах, однако обновление необходимо производить атомарно, что требует инвализации кэша.

На этапе схлопывания фрагментов требуется атомарно обновить массив [math]parent(u)[/math] для каждого добавляемого в MST ребра. В зависимости от реализации параллельной структуры Union-Find корни фрагментов могут находиться ближе к началу массива, что позволяет закешировать эту наиболее часто читаемую область. Требование атомарности, однако, ограничивает эффект от такого кэширования.

2.2.1 Locality of implementation

2.2.1.1 Structure of memory access and a qualitative estimation of locality

Рисунок 3. Алгоритм Борувки. Общий профиль обращений в память

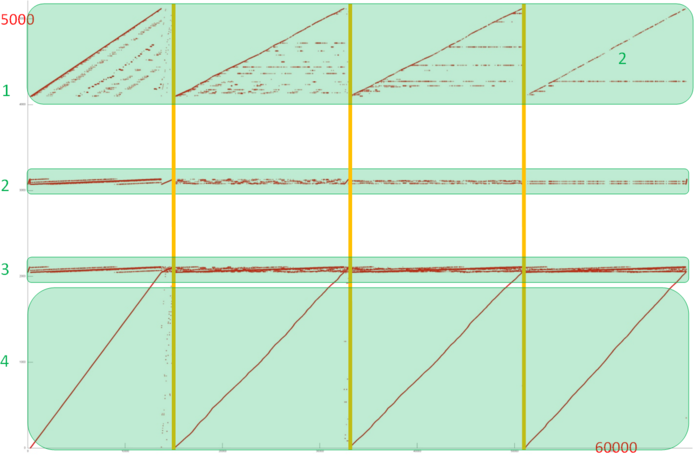
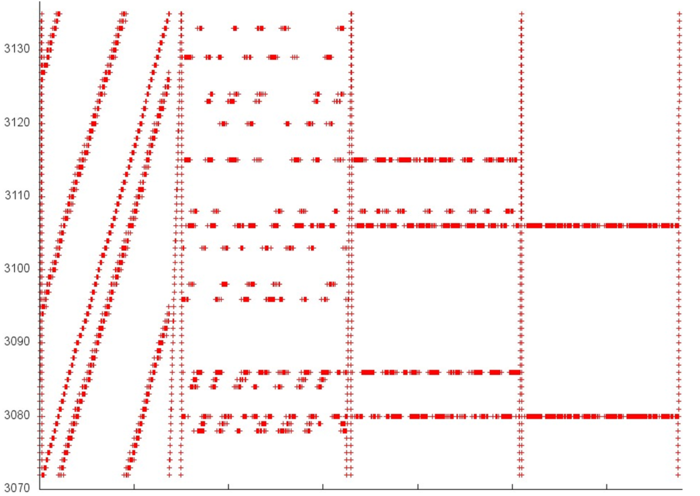
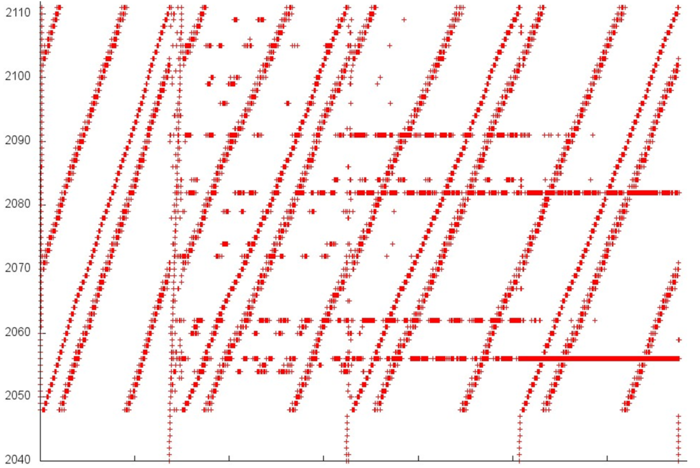
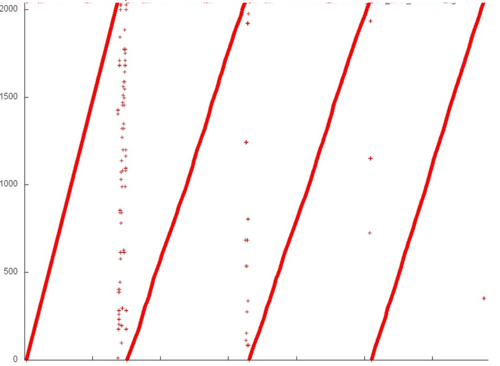
На рис. 3 представлен профиль обращений в память для реализации алгоритма Борувки. Этот алгоритм, как и большинство графовых алгоритмов, обладает нерегулярной структурой. Сразу нужно отметить, что локальность реализаций таких алгоритмов во многом зависит от структуры входного графа и может существенно меняться. В данном случае мы рассматриваем лишь один из возможных вариантов.

Можно увидеть, что общий профиль состоит из 4 достаточно схожих этапов (разделены на рис. 3 вертикальными линиями). Однако поскольку этот профиль не обладает регулярной структурой, лучше рассмотреть все этапы.

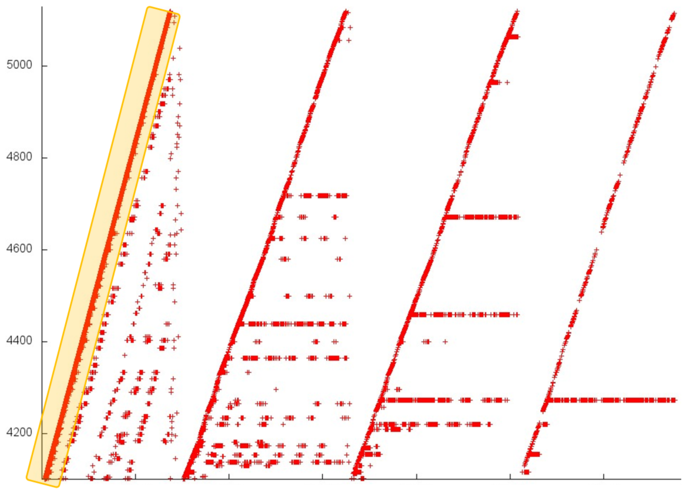
Начнем с изучения верхней части профиля (фрагмент 1 на рис. 3), которая показана на рис. 4. На каждом этапе большую часть обращений занимает последовательный перебор всех элементов данного фрагмента (выделен на рис. 4 желтым). Остальные обращения на разных этапах устроены по-разному. Если на первом этапе эти обращения разбросаны достаточно далеко друг от друга, что приводит к низкой пространственной и временной локальности, то на последнем этапе почти все обращения (не считая последовательного перебора) выполняются к одному и тому же элементу, что, естественно, характеризуется очень высокой локальностью. Подобное строение всего фрагмента приводит, скорее всего, к средним значениям и по пространственной, и по временной локальности.

Рисунок 4. Профиль обращений, фрагмент 1

Далее перейдем к изучению фрагмента 2 (рис. 5). Здесь можно увидеть, что строение каждого из 4 этапов отличается достаточно сильно. Как и в случае с фрагментом 1, каждый следующий этап обладает более высокой локальностью, однако здесь это заметно сильнее. При этом отметим, что данный фрагмент задействует всего около 60 элементов, а обращений к ним выполняется достаточно много, так что локальность в данном случае будет высока.

Рисунок 5. Профиль обращений, фрагмент 2

В целом похожая картинка наблюдается и во фрагменте 3. На рис. 6 видны 4 этапа со схожей структурой, и также задействовано около 60 элементов, что позволяет говорить о высокой локальности данного фрагмента.

Рисунок 6. Профиль обращений, фрагмент 3

Отдельное рассмотрение фрагмента 4 (рис. 7) позволяет увидеть, что локальность здесь определяется 4 последовательными переборами всех элементов данного фрагмента. Эти переборы обладают стандартной структурой – шаг по памяти 1, только 1 обращение к каждому элементу; небольшое искривление данных переборов вызвано нерегулярной активностью в других фрагментах, которая приводит к искажению визуального представления профиля. Подобный набор обращений обладает высокой пространственной, но низкой временной локальностью.

Рисунок 7. Профиль обращений, фрагмент 4

Таким образом, фрагменты 2 и 3 характеризуются высокой локальностью, другие 2 фрагмента – средней локальностью. А поскольку большая часть обращений приходится именно на фрагменты 2 и 3, можно предположить, что общая локальность должна быть достаточно высока.

2.2.1.2 Quantitative estimation of locality

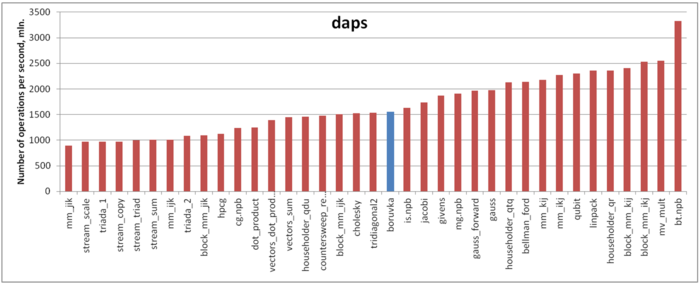
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рисунке 8 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность работы с памятью в данном случае достаточно неплоха – значение daps сравнимо, например, со значением для реализации метода Холецкого. Однако это значение заметно ниже самых производительных реализаций алгоритмов (например, теста Linpack), что в целом неудивительно в случае графовых алгоритмов, традиционно неэффективно работающих с памятью.

Рисунок 8. Сравнение значений оценки daps

2.3 Possible methods and considerations for parallel implementation of the algorithm

Программа, реализующая алгоритм Борувки, состоит из двух частей:

1. части, отвечающей за общую координацию вычислений

2. части, отвечающей за параллельные вычисления на многоядерных CPU или GPU.

Описанный выше последовательный алгоритм не может применяться в параллельной программе: в реализации [math]MERGE[/math] результаты операций [math]FIND(u)[/math] и [math]FIND(v)[/math] могут постоянно меняться, что приведёт к race condition. Параллельный вариант алгоритма описан в статье.

1. Каждой вершине v соответствует запись [math]A[v] = { parent, rank }[/math]. Изначально [math]A[v] := { v, 0 }[/math].

2. Вспомогательная операция [math]UPDATE(v, rank_v, u, rank_u)[/math]:

old := A[v]

if old.parent != v or old.rank != rank_v then return false

new := { u, rank_u }

return CAS(A[v], old, new)

3. Операция [math]FIND(v)[/math]:

   while v != A[v].parent do
       u := A[v].parent
       CAS(A[v].parent, u, A[u].parent)
       v := A[u].parent
   return v

4. Операция UNION(u, v):

   while true do
       (u, v) := (FIND(u), FIND(v))
       if u = v then return false
       (rank_u, rank_v) := (A[u].rank, A[v].rank)
       if (A[u].rank, u) > (A[v].rank, v) then
           swap((u, rank_u), (v, rank_v))
       if UPDATE(u, rank_u, v, rank_u) then
           if rank_u = rank_v then
               UPDATE(v, rank_v, v, rank_v + 1)
           return true

Для описанной версии алгоритма гарантируется свойство wait-free. На практике может использоваться упрощённая версия без подсчёта рангов, обладающая более слабым свойством lock-free, но в ряде случаев выигрывающая по скорости.

2.4 Scalability of the algorithm and its implementations

2.4.1 Scalability of the algorithm

Возможность обрабатывать фрагменты независимо означает хорошую масштабируемость алгоритма. Сдерживающими факторами являются

1. пропускная способность памяти при чтении данных графа
2. соперничество потоков при выполнении атомарных операций с памятью
3. барьерная синхронизация после каждого подшага алгоритма.

2.4.2 Scalability of of the algorithm implementation

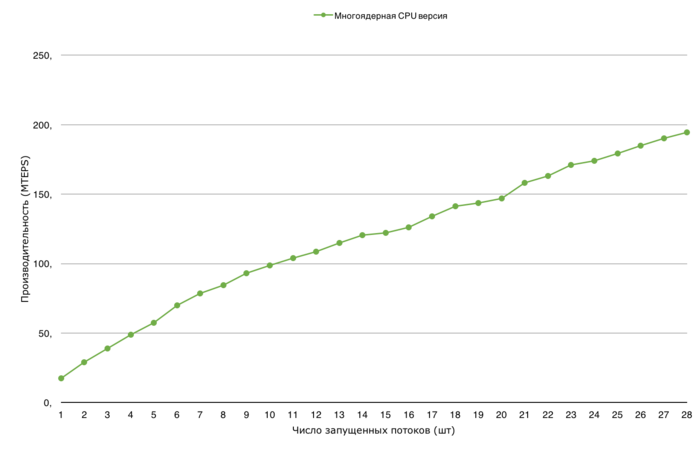
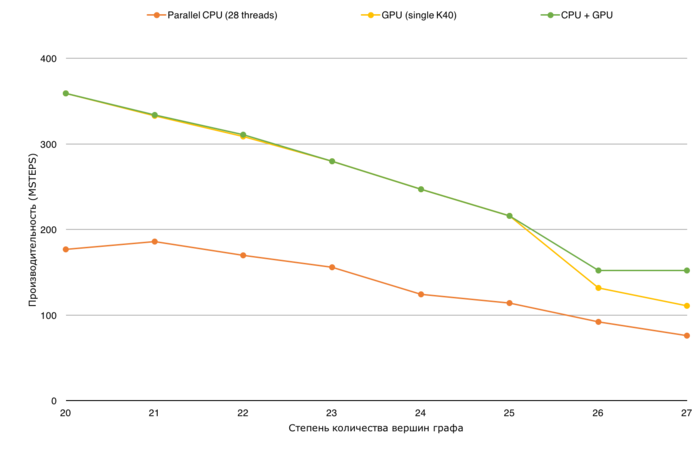
Проведём исследование масштабируемости параллельной реализации алгоритма Борувки согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2 Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [1 : 28] с шагом 1;
• размер графа [2^20 : 2^27].

Проведем отдельные исследования сильной масштабируемости и масштабируемости вширь реализации алгоритма Борувки.

Производительность определена как TEPS (от англ. Traversed Edges Per Second), то есть число ребер графа, который алгоритм обрабатывает в секунду. С помощью данной метрики можно сравнивать производительность для различных размеров графа, оценивая, насколько понижается эффективность обработки графа при увеличении его размера

Рисунок 3. Параллельная реализация алгоритма Борувки масштабируемость CPU версии: производительность в зависимости от числа запущенных CPU-потоков.

Рисунок 4. Параллельная реализация алгоритма Борувки масштабируемость различных версий реализации алгоритма: производительность в зависимости от размера графа

2.5 Dynamic characteristics and efficiency of the algorithm implementation

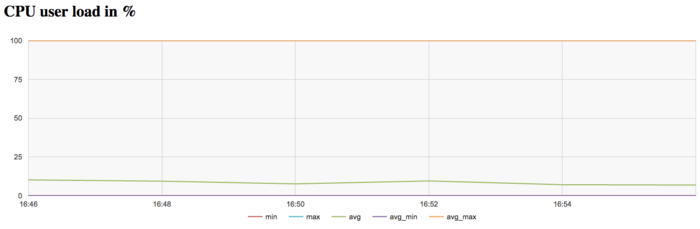
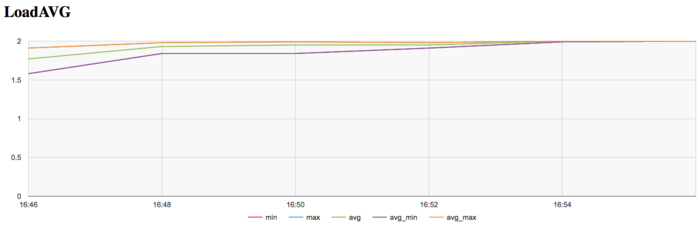
Для проведения экспериментов использовалась реализация алгоритма Борувки, реализованная для CPU. Все результаты получены на суперкомпьютере «Ломоносов-2». Использовались процессоры Intel Xeon E5-2697v3, задача решалась для графа большого размера на одном узле. На рисунках показана эффективность реализации алгоритма Борувки, запуск проводился на 1 узле для графа 2^27, выполнялась 1 итерация.

Рисунок 9. График загрузки CPU при выполнении алгоритма Борувки

На графике загрузки процессора видно, что почти все время работы программы не загружены и средний уровень загрузки составляет около 10%. Это нормальная картина для программ, запущенных c использованием одного ядра в реализации.

Рисунок 10. График числа процессов, ожидающих вхождения в стадию счета (Loadavg), при работе алгоритма Борувки

На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно на уровне 2. Это указывает на постоянную загрузку аппаратных ресурсов не более чем 2 процессами, однако их число для узла слишком мало, что с одной стороны может указывать на не очень рациональные использование ресурсов.

Рисунок 11. График кэш-промахов L1 в секунду при работе алгоритма Борувки

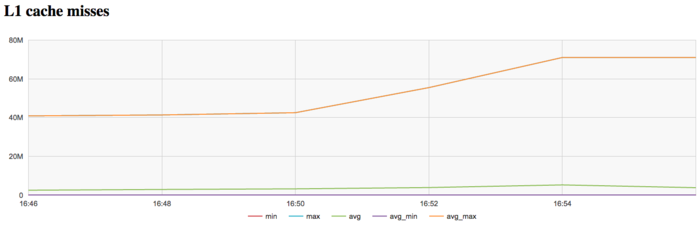
На графике кэш-промахов первого уровня видно, что число промахов очень высокое и находится на уровне 40 млн/сек . Интересен факт увеличения числа промахов к концу итерации до уровня в 70 млн/сек.

Рисунок 12. График кэш-промахов L1 в секунду при работе алгоритма Борувки

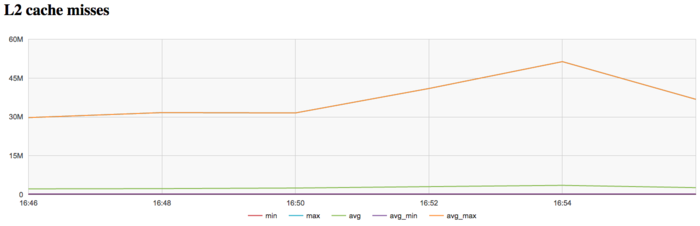
На графике кэш-промахов второго уровня видно, что число промахов достаточно тоже высокое и находится на уровне 30 млн/сек . На графике промахов второго уровня факт увеличения числа промахов к концу итерации проявляется более явно и увеличивается до значения в 50млн/сек.

Рисунок 13. График кэш-промахов L3 в секунду при работе алгоритма Борувки

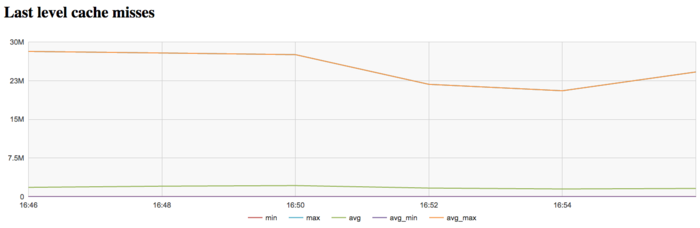
На графике кэш-промахов последнего уровня видно, что число промахов тоже достаточно большое и составляет около 30 млн/сек по всем узлам. Эт указывает на то, что задача очень плохо укладывается в кэш-память, и программа постоянно работает с оперативной памятью, что объясняется очень большим размером использованного графа.

Рисунок 13. График скорости передачи по сети Infiniband в байт/сек при работе алгоритма Борувки

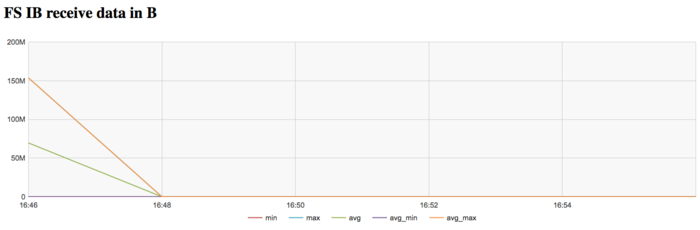
На графике скорости передачи данных по сети Infiniband наблюдается достаточно высокая интенсивность использования сети на кпервом этапе. Это объясняется программной логикой, которая предполагает чтение графа из файла с диска, коммуникации с которым происходят на Ломоносов-2 через выделенную для этих задач сеть Infiniband.

Рисунок 14. График скорости передачи по сети Infiniband в пакетах/сек при работе алгоритма Борувки

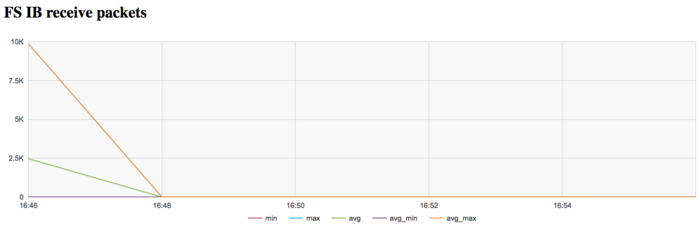
На графике скорости передачи данных в пакетах в секунду наблюдается аналогичная картина очень высокой интенсивности на первом этапе выполнения задачи. Далее сеть почти не используется.

В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала стабильно интенсивно, однако очень неэффективно использовала память из-за очень большого размера графа.

2.7 Existing implementations of the algorithm

• C++, MPI: Parallel Boost Graph Library; функции dense_boruvka_minimum_spanning_tree, boruvka_then_merge, boruvka_mixed_merge сочетают алгоритм Борувки и алгоритм Крускала.