Difference between revisions of "DCSC algorithm for finding the strongly connected components"
| [quality revision] | [checked revision] |
| (36 intermediate revisions by one other user not shown) | |||
| Line 14: | Line 14: | ||
=== General description of the algorithm === | === General description of the algorithm === | ||
| − | '''Алгоритм DCSC'''<ref>Fleischer, Lisa K, Bruce Hendrickson, and Ali Pınar. “On Identifying Strongly Connected Components in Parallel.” In Lecture Notes in Computer Science, Volume 1800, Springer, 2000, pp. 505–11. doi:10.1007/3-540-45591-4_68.</ref><ref>McLendon, William, III, Bruce Hendrickson, Steven J Plimpton, and Lawrence Rauchwerger. “Finding Strongly Connected Components in Distributed Graphs.” Journal of Parallel and Distributed Computing 65, no. 8 (August 2005): 901–10. doi:10.1016/j.jpdc.2005.03.007.</ref><ref>Hong, Sungpack, Nicole C Rodia, and Kunle Olukotun. “On Fast Parallel Detection of Strongly Connected Components (SCC) in Small-World Graphs,” Proceeedings of SC'13, 1–11, New York, New York, USA: ACM Press, 2013. doi:10.1145/2503210.2503246.</ref> ( | + | '''Алгоритм DCSC'''<ref>Fleischer, Lisa K, Bruce Hendrickson, and Ali Pınar. “On Identifying Strongly Connected Components in Parallel.” In Lecture Notes in Computer Science, Volume 1800, Springer, 2000, pp. 505–11. doi:10.1007/3-540-45591-4_68.</ref><ref>McLendon, William, III, Bruce Hendrickson, Steven J Plimpton, and Lawrence Rauchwerger. “Finding Strongly Connected Components in Distributed Graphs.” Journal of Parallel and Distributed Computing 65, no. 8 (August 2005): 901–10. doi:10.1016/j.jpdc.2005.03.007.</ref><ref>Hong, Sungpack, Nicole C Rodia, and Kunle Olukotun. “On Fast Parallel Detection of Strongly Connected Components (SCC) in Small-World Graphs,” Proceeedings of SC'13, 1–11, New York, New York, USA: ACM Press, 2013. doi:10.1145/2503210.2503246.</ref> (Divide and Conquer Strong Components) finds [[Связность в графах|strongly connected components]] of a directed graph with the expected complexity <math>O(|V| \ln |V|)</math> (assuming that the node degrees are bounded by a constant). |
| − | + | In the literature on GPU implementations of the algorithm, it is typically called the Forward-Backward algorithm (shortly, the FB-algorithm). <ref> Jiˇr ́ı Barnat, Petr Bauch, Lubosˇ Brim, and Milan Cˇesˇka. Computing Strongly Connected Components in Parallel on CUDA. Faculty of Informatics, Masaryk University, Botanicka ́ 68a, 60200 Brno, Czech Republic. </ref> | |
| − | + | From the outset, the algorithm was designed for parallel realization. Indeed, at each step, it finds a strongly connected component and selects up to three subsets in the graph that contain other connected components and can be processed in parallel. Moreover, the selection of these subsets and the strongly connected component can be done in parallel (using parallel breadth-first searches). It should be noted that the iterations of breadth-first searches need not to be synchronized because their aim is to determine reachable nodes rather than to find the distances to these nodes. | |
| − | + | The algorithm is well suitable for graphs that consist of a small number of large strongly connected components. A significant increase in the number of strongly connected components implies that the complexity of the algorithm also increases significantly (proportionally to the number of components). For this reason, the algorithm may become less efficient than Tarjan's algorithm, which selects strongly connected components in the course of one graph traversal. | |
| − | + | The following modification of the algorithm was proposed to improve its efficiency for graphs with a large number of trivial (that is, of size 1 or 2) strongly connected components: prior to executing the classical algorithm, the so-called Trim step is performed. This step, described in a later section, allows one to select all the trivial strongly connected components. For instance, for RMAT graphs, an application of the Trim step leaves in the graph only a few large strongly connected components. For such components, the complexity of the algorithm is not large. | |
=== Mathematical description of the algorithm === | === Mathematical description of the algorithm === | ||
| − | + | Let <math>v</math> be a node of the graph. Define the following sets of nodes: | |
| − | ⎯ <math>Fwd(v)</math> – | + | ⎯ <math>Fwd(v)</math> – the nodes reachable from <math>v</math> . |
| − | ⎯ <math>Pred(v)</math> – | + | ⎯ <math>Pred(v)</math> – the nodes from which <math>v</math> is reachable (equivalently, the nodes reachable from <math>v</math> in the graph obtained by reverting all the arcs in <math>G</math>). |
| − | + | By using these sets, all the nodes of the graph can be partitioned into four regions: | |
⎯ <math>V_1 = Fwd(v) \cap Pred(v) </math> | ⎯ <math>V_1 = Fwd(v) \cap Pred(v) </math> | ||
| Line 42: | Line 42: | ||
⎯ <math>V_4 = V \setminus Pred(v) \setminus Fwd(v)</math> | ⎯ <math>V_4 = V \setminus Pred(v) \setminus Fwd(v)</math> | ||
| − | + | Then one can assert the following: | |
| − | 1. | + | 1. The region <math>V_1</math> is a strongly connected component. |
| − | 2. | + | 2. Every other strongly connected component is completely contained in one of the regions <math>V_2</math>, <math>V_3</math>, or <math>V_4</math>. |
=== Computational kernel of the algorithm === | === Computational kernel of the algorithm === | ||
| − | + | The basic computational operations of the algorithm are the search for nodes reachable from the chosen node <math>v</math> and the search for nodes from which <math>v</math> is reachable. Both these operations can be implemented by using breadth-first searches in the following manner: | |
| − | 1. | + | 1. The node <math>v_0</math> is placed at the beginning of queue and marked as a visited node. |
| − | 2. | + | 2. Remove the front node <math>v</math> from the queue. For all the arcs <math>(v, u)</math> outcoming from <math>v</math>, verify whether the node <math>u</math> was visited. If it was, then <math>u</math> is placed at the beginning of queue. |
| − | 3. | + | 3. As long as the queue is not empty, go to step 2. |
=== Macro structure of the algorithm === | === Macro structure of the algorithm === | ||
| − | + | The DCSC algorithm consists of the following actions: | |
| − | 1. | + | 1. Place the set <math>V</math> to a queue. |
| − | 2. | + | 2. Process the queue in parallel. For each element in <math>V</math>: |
| − | + | (a) Choose an arbitrary pivot node <math>v \in V</math>. | |
| − | + | (b) Compute the sets <math>Fwd(v)</math> and <math>Pred(v)</math> (these two computations can be executed in parallel; in addition, as indicated above, each of them is well parallelizable). | |
| − | + | (c) Add the set <math> V_1</math> to the list of strongly connected components. | |
| − | + | (d) Add the sets <math> V_2</math>, <math>V_3</math>, and <math>V_4</math> to the queue. | |
| − | 3. | + | 3. The algorithm terminates when the queue is empty and there are no active processes left. |
| − | + | To improve the balance of loading at the first steps of the algorithm, one can simultaneously choose several pivot nodes rather than a single node. If these pivots belong to different strongly connected components, then the result is a partition of the graph into numerous regions, which thereafter are processed in parallel. | |
| − | + | An important modification of the DCSC algorithm consists in executing a Trim step before the basic calculations. The Trim step can be described as follows: | |
| − | 1. | + | 1. Mark all <math>v \in V</math> as active nodes. |
| − | 2. | + | 2. For each node <math>v</math>, calculate the number <math>in(v)</math> of incoming arcs and the number <math>out(v)</math> of outcoming arcs <math>(v, u) \in E</math> such that <math>u</math> is an active node. |
| − | 3. | + | 3. Mark as nonactive all the nodes <math>v \in V</math> for which at least one of the numbers <math>in(v)</math> and <math>out(v)</math> is zero. |
| − | 4. | + | 4. Go to step 2 until the number of active nodes ceases to very. |
| − | + | Moreover, the chosen scheme for storing the graph may require that the transpose of this graph be first constructed. This may make more efficient the implementation of the Trim step and the search (within the computational kernel of the algorithm) for nodes from which the given node <math>v</math> is reachable. | |
=== Implementation scheme of the serial algorithm === | === Implementation scheme of the serial algorithm === | ||
| − | + | The serial algorithm is implemented by the following pseudocode: | |
| − | ''' | + | '''Input data''': |
| − | + | graph with nodes ''V'' and arcs ''E''; | |
| − | ''' | + | '''Output data''': indices of the strongly connected components ''c(v)'' for each node ''v'' ∈ ''V''. |
<source lang="C++"> | <source lang="C++"> | ||
| Line 146: | Line 146: | ||
</source> | </source> | ||
| − | bfs | + | Here, bfs are conventional breadth-first searches described in the corresponding section. Such a search results in finding all the nodes of the graph <math> G </math> that are reachable from the given node <math> p </math>. |
=== Serial complexity of the algorithm === | === Serial complexity of the algorithm === | ||
| − | + | Assume that all the nodes of a graph have degrees bounded by a constant. Then the expected serial complexity of the algorithm is <math>O(|V| \ln(|V|))</math>. | |
=== Information graph === | === Information graph === | ||
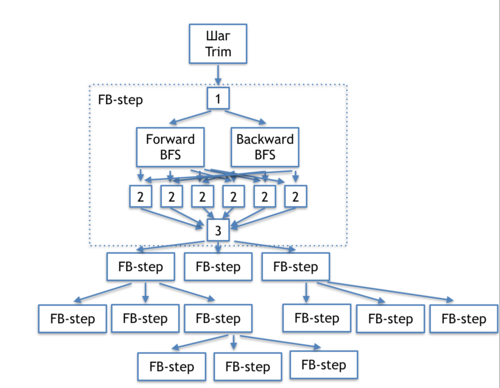
| − | + | The information graph of the DCSC algorithm shown in figure 1 demonstrates relations between the basic parts of the algorithm. | |
| − | [[file:DCSC_full_ig.png|thumb|center|500px| | + | [[file:DCSC_full_ig.png|thumb|center|500px|Figure 1. Information graph of the DCSC algorithm (Forward-Backward-Trim).]] |
| − | + | These basic parts are: initial Trim step; choice of the pivot node [1]; breadth-first searches performed in the direct graph and its transpose (forward и backward BFS); handling the results of searches [2]; test for the necessity to continue the recursion [3]; and recursive calls of the FB-step. Below, we present more detailed information graphs for each of the parts, as well as the transcript of the corresponding operations. In the next section, we assess the parallelization resource of each part. | |
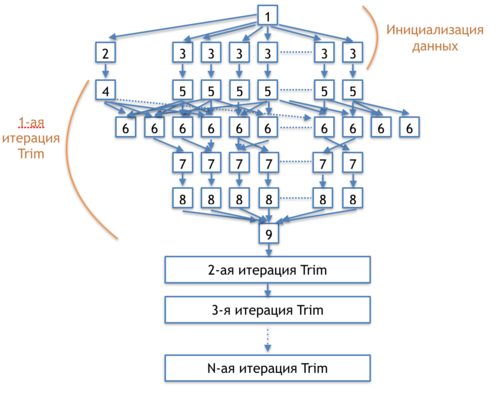
| − | + | The information graph of the Trim step is shown in figure 2. | |
| − | [[file:DCSC_trim_step.png|thumb|center|500px| | + | [[file:DCSC_trim_step.png|thumb|center|500px|Figure 2. Information graph of the Trim step in the DCSC algorithm.]] |
| − | [1] - | + | [1] - memory allocation for the arrays storing the numbers of incoming and outcoming arcs and the array of active nodes |
| − | [2] - | + | [2] - initialization of the variable "change indicator" |
| − | [3] - | + | [3] - initialization of the array for strongly connected components and the array of active nodes |
| − | [4] - | + | [4] - assignment of the value "no changes" to the change indicator |
| − | [5] - | + | [5] - zeroing out the arrays for the numbers of incoming and outcoming arcs |
| − | [6] - | + | [6] - verification whether the nodes at the ends of each arc are active; increasing the number of incoming/outcoming arcs for the corresponding nodes; update the value of the change indicator |
| − | [7] - | + | [7] - activity test for all the nodes of the graph |
| − | [8] - | + | [8] - numbering of the strongly connected components with zero degree of incoming or outcoming arcs |
| − | [9] - | + | [9] - verification whether any changes occurred at step 6; transition to the next iteration |
| − | + | The information graph of the BFS stage (Forward и Backward BFS) is shown at the corresponding section ([[Breadth_first_search_(BFS)]]). | |
=== Parallelization resource of the algorithm === | === Parallelization resource of the algorithm === | ||
| − | + | From the outset, the algorithm was designed for parallel realization. It has several levels of parallelism. | |
| − | + | At the upper level, the DCSC algorithm is able to execute in parallel the FB-steps shown in figure 1. Thus, at each step, the algorithm can recursively generate up to three new parallel processes; their total number is equal to the number of strongly connected components. Moreover, the breadth-first searches in the original graph and its transpose are independent and can also be performed in parallel. Thus, up to | |
| + | <math> 2*u/log|u|</math> parallel processes can be executed at the upper level, where <math> u </math> is the number of strongly connected components in the graph. It is important to note that the FB-steps of the same level (as well as the subsequent recursive steps) are completely independent in terms of data because they concern disjoint sets of graph nodes. Consequently, they can even be performed on different cores. Moreover, the composite steps of the algorithm (the breadth-first search and the Trim step) also have a considerable parallelization potential, which is described below. | ||
| − | + | The Trim stage, whose information graph is shown in figure 2, has a considerable parallelization resource: the only serial steps are the initializations of arrays and variables [(1),(2)] and test (9) for loop termination. Operations (3),(5),(7), and (8) are completely independent and can be performed in parallel. The number of these operations is <math>O(|V|)</math>. Tests and data updatings in operation (6) can also be executed in parallel; however, the data updatings must be done in the atomic manner. The number of operations in (6) is <math>O(E)</math>. Thus, almost all steps of the Trim stage can be performed in the parallel mode, and the number of operations executed in parallel is <math>|V|</math> or <math>|E|</math>. For large graphs, the values <math>|V|</math> and <math>|E|</math> are fairly large. Hence, the parallelization potential of this stage in the algorithm is very significant; it is sufficient for the full loading of modern computational cores/coprocessors. In addition, operations (3),(5),(7), and (8) can be successfully vectorized. | |
| − | + | The parallelization resource of the breadth-first search is described in detail in the corresponding section ([[Breadth_first_search_(BFS)]]). Depending on the choice of a format for storing graphs, the parallel implementation of the breadth-first search may have linear or (in the worst case) quadratic complexity. | |
| − | + | In the case of linear parallelization, the breadth-first search performs at each case <math>O(n)</math> parallel operations, where <math>n</math> is the number of nodes added for inspection at the preceding step. Prior to the start of the search, the source node is placed for inspection; at the first step, all the not yet visited nodes adjacent to the source node are added; at the second step, all the not yet visited nodes adjacent to the nodes of the first step are added; etc. It is difficult to estimate the maximum (or even average) number of nodes at each step because the number of steps in the algorithm and the number of reachable nodes, as well as the pattern of their relations, are only determined by the structure of the input graph. If all the nodes are reachable and the number of steps in the breadth-first search is <math> r </math>, then the average number of nodes processed at each step in parallel is <math> O(|V|)/r </math>. It is important to note that the maximum level of parallelism is attained at the middle steps of the algorithm, whereas the number of nodes processed at the initial and final steps may be small. | |
| − | + | In the case of quadratic parallelization, the breadth-first search traverses at each step all the arcs of the graph, thus performing <math>O(|E|)</math> parallel operations. This is identical to the similar estimate for the trim step. Moreover, if the implementation uses lists of graph nodes, then the breadth-first search can be vectorized. | |
| − | + | Thus, at the initial stage, the algorithm can perform <math>O(|V|)</math> or <math>O(|E|)</math> parallel operations. Then <math>O(log(u))</math> steps are carried out; on the average, each step involves <math>2*u/O(log(u))</math> breadth-first searches, which also have an inherent parallelization resource. Namely, for a quadratic implementation, each breadth-first search performs at each step <math>O(|E|)</math> parallel operations. | |
| − | + | The height and width of the parallel form depend on the structure of graph (that is, on the number and location of strongly connected components) because the FB steps depend in a similar way on the input data. | |
=== Input and output data of the algorithm === | === Input and output data of the algorithm === | ||
| − | ''' | + | '''Input data''': graph <math>G(V, E)</math> with <math>|V|</math> nodes <math>v_i</math> and <math>|E|</math> arcs <math>e_j = (v^{(1)}_{j}, v^{(2)}_{j})</math>. |
| − | ''' | + | '''Size of the input data''': <math>O(|V| + |E|)</math>. |
| − | ''' | + | '''Output data''': for each node <math>v</math> of the original graph, the index |
| + | <math> c(v) </math> of the strongly connected component to which this node belongs. Nodes belonging to the same strongly connected component produce identical indices. | ||
| − | ''' | + | '''Size of the output data''': <math>O(|V|)</math>. |
=== Properties of the algorithm === | === Properties of the algorithm === | ||
| − | + | The computational kernel of the algorithm is based on breadth-first searches; consequently, many of the properties (locality, scalability) of the former and latter algorithms are similar. | |
== Software implementation of the algorithm == | == Software implementation of the algorithm == | ||
| Line 220: | Line 222: | ||
=== Implementation peculiarities of the serial algorithm === | === Implementation peculiarities of the serial algorithm === | ||
| − | |||
| − | |||
| − | |||
| − | |||
=== Possible methods and considerations for parallel implementation of the algorithm === | === Possible methods and considerations for parallel implementation of the algorithm === | ||
| − | === | + | === Run results === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Conclusions for different classes of computer architecture === | === Conclusions for different classes of computer architecture === | ||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
Latest revision as of 15:11, 6 July 2022
| Алгоритм DCSC поиска компонент сильной связности | |
| Sequential algorithm | |
| Serial complexity | O(|V| \ln(|V|)) |
| Input data | O(|V| + |E|) |
| Output data | O(|V|) |
| Parallel algorithm | |
| Parallel form height | C * O(ln(u)) |
| Parallel form width | O(|E|) |
Primary author of this description: I.V.Afanasyev.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Алгоритм DCSC[1][2][3] (Divide and Conquer Strong Components) finds strongly connected components of a directed graph with the expected complexity O(|V| \ln |V|) (assuming that the node degrees are bounded by a constant).
In the literature on GPU implementations of the algorithm, it is typically called the Forward-Backward algorithm (shortly, the FB-algorithm). [4]
From the outset, the algorithm was designed for parallel realization. Indeed, at each step, it finds a strongly connected component and selects up to three subsets in the graph that contain other connected components and can be processed in parallel. Moreover, the selection of these subsets and the strongly connected component can be done in parallel (using parallel breadth-first searches). It should be noted that the iterations of breadth-first searches need not to be synchronized because their aim is to determine reachable nodes rather than to find the distances to these nodes.
The algorithm is well suitable for graphs that consist of a small number of large strongly connected components. A significant increase in the number of strongly connected components implies that the complexity of the algorithm also increases significantly (proportionally to the number of components). For this reason, the algorithm may become less efficient than Tarjan's algorithm, which selects strongly connected components in the course of one graph traversal.
The following modification of the algorithm was proposed to improve its efficiency for graphs with a large number of trivial (that is, of size 1 or 2) strongly connected components: prior to executing the classical algorithm, the so-called Trim step is performed. This step, described in a later section, allows one to select all the trivial strongly connected components. For instance, for RMAT graphs, an application of the Trim step leaves in the graph only a few large strongly connected components. For such components, the complexity of the algorithm is not large.
1.2 Mathematical description of the algorithm
Let v be a node of the graph. Define the following sets of nodes:
⎯ Fwd(v) – the nodes reachable from v .
⎯ Pred(v) – the nodes from which v is reachable (equivalently, the nodes reachable from v in the graph obtained by reverting all the arcs in G).
By using these sets, all the nodes of the graph can be partitioned into four regions:
⎯ V_1 = Fwd(v) \cap Pred(v)
⎯ V_2 = Fwd(v) \setminus Pred(v)
⎯ V_3 = Pred(v) \setminus Fwd(v)
⎯ V_4 = V \setminus Pred(v) \setminus Fwd(v)
Then one can assert the following:
1. The region V_1 is a strongly connected component.
2. Every other strongly connected component is completely contained in one of the regions V_2, V_3, or V_4.
1.3 Computational kernel of the algorithm
The basic computational operations of the algorithm are the search for nodes reachable from the chosen node v and the search for nodes from which v is reachable. Both these operations can be implemented by using breadth-first searches in the following manner:
1. The node v_0 is placed at the beginning of queue and marked as a visited node.
2. Remove the front node v from the queue. For all the arcs (v, u) outcoming from v, verify whether the node u was visited. If it was, then u is placed at the beginning of queue.
3. As long as the queue is not empty, go to step 2.
1.4 Macro structure of the algorithm
The DCSC algorithm consists of the following actions:
1. Place the set V to a queue.
2. Process the queue in parallel. For each element in V:
(a) Choose an arbitrary pivot node v \in V.
(b) Compute the sets Fwd(v) and Pred(v) (these two computations can be executed in parallel; in addition, as indicated above, each of them is well parallelizable).
(c) Add the set V_1 to the list of strongly connected components.
(d) Add the sets V_2, V_3, and V_4 to the queue.
3. The algorithm terminates when the queue is empty and there are no active processes left.
To improve the balance of loading at the first steps of the algorithm, one can simultaneously choose several pivot nodes rather than a single node. If these pivots belong to different strongly connected components, then the result is a partition of the graph into numerous regions, which thereafter are processed in parallel.
An important modification of the DCSC algorithm consists in executing a Trim step before the basic calculations. The Trim step can be described as follows:
1. Mark all v \in V as active nodes.
2. For each node v, calculate the number in(v) of incoming arcs and the number out(v) of outcoming arcs (v, u) \in E such that u is an active node.
3. Mark as nonactive all the nodes v \in V for which at least one of the numbers in(v) and out(v) is zero.
4. Go to step 2 until the number of active nodes ceases to very.
Moreover, the chosen scheme for storing the graph may require that the transpose of this graph be first constructed. This may make more efficient the implementation of the Trim step and the search (within the computational kernel of the algorithm) for nodes from which the given node v is reachable.
1.5 Implementation scheme of the serial algorithm
The serial algorithm is implemented by the following pseudocode:
Input data: graph with nodes V and arcs E; Output data: indices of the strongly connected components c(v) for each node v ∈ V.
compute_scc_with_trim(G)
{
G’ = transpose(G)
G = trim(G)
compute_scc()
}
compute_scc(V, G, G’)
{
p = pivot(V)
fwd = bfs(G, p);
pred = bfs(G’, p);
compute_scc(fwd / pred, G, G’)
compute_scc(pred / fwd, G, G’)
compute_scc(V / pred / fwd, G, G’)
}
pivot(V)
{
return random v in V
}
trim(G)
{
for each v in V(G)
active[v] = true
changes = false
do
{
for each v in V
in_deg(v) = compute_in_degree(v)
out_deg(v) = compute_out_degree(v)
for each v in V
if (in_deg[v] == 0 || out_deg[v] == 0)
active[v] = false
changes = true
} while (!changes)
return active
}
Here, bfs are conventional breadth-first searches described in the corresponding section. Such a search results in finding all the nodes of the graph G that are reachable from the given node p .
1.6 Serial complexity of the algorithm
Assume that all the nodes of a graph have degrees bounded by a constant. Then the expected serial complexity of the algorithm is O(|V| \ln(|V|)).
1.7 Information graph
The information graph of the DCSC algorithm shown in figure 1 demonstrates relations between the basic parts of the algorithm.
These basic parts are: initial Trim step; choice of the pivot node [1]; breadth-first searches performed in the direct graph and its transpose (forward и backward BFS); handling the results of searches [2]; test for the necessity to continue the recursion [3]; and recursive calls of the FB-step. Below, we present more detailed information graphs for each of the parts, as well as the transcript of the corresponding operations. In the next section, we assess the parallelization resource of each part.
The information graph of the Trim step is shown in figure 2.
[1] - memory allocation for the arrays storing the numbers of incoming and outcoming arcs and the array of active nodes
[2] - initialization of the variable "change indicator"
[3] - initialization of the array for strongly connected components and the array of active nodes
[4] - assignment of the value "no changes" to the change indicator
[5] - zeroing out the arrays for the numbers of incoming and outcoming arcs
[6] - verification whether the nodes at the ends of each arc are active; increasing the number of incoming/outcoming arcs for the corresponding nodes; update the value of the change indicator
[7] - activity test for all the nodes of the graph
[8] - numbering of the strongly connected components with zero degree of incoming or outcoming arcs
[9] - verification whether any changes occurred at step 6; transition to the next iteration
The information graph of the BFS stage (Forward и Backward BFS) is shown at the corresponding section (Breadth_first_search_(BFS)).
1.8 Parallelization resource of the algorithm
From the outset, the algorithm was designed for parallel realization. It has several levels of parallelism.
At the upper level, the DCSC algorithm is able to execute in parallel the FB-steps shown in figure 1. Thus, at each step, the algorithm can recursively generate up to three new parallel processes; their total number is equal to the number of strongly connected components. Moreover, the breadth-first searches in the original graph and its transpose are independent and can also be performed in parallel. Thus, up to 2*u/log|u| parallel processes can be executed at the upper level, where u is the number of strongly connected components in the graph. It is important to note that the FB-steps of the same level (as well as the subsequent recursive steps) are completely independent in terms of data because they concern disjoint sets of graph nodes. Consequently, they can even be performed on different cores. Moreover, the composite steps of the algorithm (the breadth-first search and the Trim step) also have a considerable parallelization potential, which is described below.
The Trim stage, whose information graph is shown in figure 2, has a considerable parallelization resource: the only serial steps are the initializations of arrays and variables [(1),(2)] and test (9) for loop termination. Operations (3),(5),(7), and (8) are completely independent and can be performed in parallel. The number of these operations is O(|V|). Tests and data updatings in operation (6) can also be executed in parallel; however, the data updatings must be done in the atomic manner. The number of operations in (6) is O(E). Thus, almost all steps of the Trim stage can be performed in the parallel mode, and the number of operations executed in parallel is |V| or |E|. For large graphs, the values |V| and |E| are fairly large. Hence, the parallelization potential of this stage in the algorithm is very significant; it is sufficient for the full loading of modern computational cores/coprocessors. In addition, operations (3),(5),(7), and (8) can be successfully vectorized.
The parallelization resource of the breadth-first search is described in detail in the corresponding section (Breadth_first_search_(BFS)). Depending on the choice of a format for storing graphs, the parallel implementation of the breadth-first search may have linear or (in the worst case) quadratic complexity.
In the case of linear parallelization, the breadth-first search performs at each case O(n) parallel operations, where n is the number of nodes added for inspection at the preceding step. Prior to the start of the search, the source node is placed for inspection; at the first step, all the not yet visited nodes adjacent to the source node are added; at the second step, all the not yet visited nodes adjacent to the nodes of the first step are added; etc. It is difficult to estimate the maximum (or even average) number of nodes at each step because the number of steps in the algorithm and the number of reachable nodes, as well as the pattern of their relations, are only determined by the structure of the input graph. If all the nodes are reachable and the number of steps in the breadth-first search is r , then the average number of nodes processed at each step in parallel is O(|V|)/r . It is important to note that the maximum level of parallelism is attained at the middle steps of the algorithm, whereas the number of nodes processed at the initial and final steps may be small.
In the case of quadratic parallelization, the breadth-first search traverses at each step all the arcs of the graph, thus performing O(|E|) parallel operations. This is identical to the similar estimate for the trim step. Moreover, if the implementation uses lists of graph nodes, then the breadth-first search can be vectorized.
Thus, at the initial stage, the algorithm can perform O(|V|) or O(|E|) parallel operations. Then O(log(u)) steps are carried out; on the average, each step involves 2*u/O(log(u)) breadth-first searches, which also have an inherent parallelization resource. Namely, for a quadratic implementation, each breadth-first search performs at each step O(|E|) parallel operations.
The height and width of the parallel form depend on the structure of graph (that is, on the number and location of strongly connected components) because the FB steps depend in a similar way on the input data.
1.9 Input and output data of the algorithm
Input data: graph G(V, E) with |V| nodes v_i and |E| arcs e_j = (v^{(1)}_{j}, v^{(2)}_{j}).
Size of the input data: O(|V| + |E|).
Output data: for each node v of the original graph, the index c(v) of the strongly connected component to which this node belongs. Nodes belonging to the same strongly connected component produce identical indices.
Size of the output data: O(|V|).
1.10 Properties of the algorithm
The computational kernel of the algorithm is based on breadth-first searches; consequently, many of the properties (locality, scalability) of the former and latter algorithms are similar.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Possible methods and considerations for parallel implementation of the algorithm
2.3 Run results
2.4 Conclusions for different classes of computer architecture
3 References
- ↑ Fleischer, Lisa K, Bruce Hendrickson, and Ali Pınar. “On Identifying Strongly Connected Components in Parallel.” In Lecture Notes in Computer Science, Volume 1800, Springer, 2000, pp. 505–11. doi:10.1007/3-540-45591-4_68.
- ↑ McLendon, William, III, Bruce Hendrickson, Steven J Plimpton, and Lawrence Rauchwerger. “Finding Strongly Connected Components in Distributed Graphs.” Journal of Parallel and Distributed Computing 65, no. 8 (August 2005): 901–10. doi:10.1016/j.jpdc.2005.03.007.
- ↑ Hong, Sungpack, Nicole C Rodia, and Kunle Olukotun. “On Fast Parallel Detection of Strongly Connected Components (SCC) in Small-World Graphs,” Proceeedings of SC'13, 1–11, New York, New York, USA: ACM Press, 2013. doi:10.1145/2503210.2503246.
- ↑ Jiˇr ́ı Barnat, Petr Bauch, Lubosˇ Brim, and Milan Cˇesˇka. Computing Strongly Connected Components in Parallel on CUDA. Faculty of Informatics, Masaryk University, Botanicka ́ 68a, 60200 Brno, Czech Republic.