Difference between revisions of "Gaussian elimination, compact scheme for tridiagonal matrices, serial variant"
| [unchecked revision] | [unchecked revision] |
| Line 1: | Line 1: | ||
{{algorithm | {{algorithm | ||
| − | | name = | + | | name = Gaussian elimination, compact scheme for tridiagonal matrices, serial variant |
| serial_complexity = <math>3n-3</math> | | serial_complexity = <math>3n-3</math> | ||
| pf_height = <math>3n-3</math> | | pf_height = <math>3n-3</math> | ||
| Line 8: | Line 8: | ||
}} | }} | ||
| − | + | Main authors: [[:ru:Участник:Frolov|Alexey Frolov]] | |
| − | == | + | == Properties and structure of the algorithm == |
| − | === | + | |
| + | === General description of the algorithm === | ||
'''Компактная схема метода Гаусса для трёхдиагональной матрицы'''<ref>Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref><ref>Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.</ref> вычисляет такое <math>LU</math>-разложение трёхдиагональной матрицы | '''Компактная схема метода Гаусса для трёхдиагональной матрицы'''<ref>Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref><ref>Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.</ref> вычисляет такое <math>LU</math>-разложение трёхдиагональной матрицы | ||
| Line 26: | Line 27: | ||
<math>LU</math>-разложение трёхдиагональной матрицы является частным случаем для [[Компактная схема метода Гаусса для плотных матриц|компактной схемы метода Гаусса]] общего вида, однако из-за специфики матрицы характеристики алгоритма кардинально меняются по сравнению с компактной схемой для плотных матриц. | <math>LU</math>-разложение трёхдиагональной матрицы является частным случаем для [[Компактная схема метода Гаусса для плотных матриц|компактной схемы метода Гаусса]] общего вида, однако из-за специфики матрицы характеристики алгоритма кардинально меняются по сравнению с компактной схемой для плотных матриц. | ||
| − | === | + | === Mathematical description of the algorithm === |
Формулы алгоритма следующие: | Формулы алгоритма следующие: | ||
| Line 38: | Line 39: | ||
<math>u_{ii} = a_{ii} - l_{i i-1} u_{i-1 i}, \quad i \in [2, n] </math> | <math>u_{ii} = a_{ii} - l_{i i-1} u_{i-1 i}, \quad i \in [2, n] </math> | ||
| − | === | + | === Computational kernel of the algorithm === |
Как видно из формул, n-1 раз повторяется одна и та же последовательность трёх операций: деление, умножение, вычитание. | Как видно из формул, n-1 раз повторяется одна и та же последовательность трёх операций: деление, умножение, вычитание. | ||
| − | === | + | === Macro structure of the algorithm === |
В качестве макровершины можно взять последовательность трёх операций: деление, умножение, вычитание. Эти макровершины выполняются в алгоритме n-1 раз. | В качестве макровершины можно взять последовательность трёх операций: деление, умножение, вычитание. Эти макровершины выполняются в алгоритме n-1 раз. | ||
| − | === | + | === Implementation scheme of the serial algorithm === |
В схеме учтено, что ряд выходных данных вычислять не нужно - они совпадают с входными. В частности, | В схеме учтено, что ряд выходных данных вычислять не нужно - они совпадают с входными. В частности, | ||
| Line 64: | Line 65: | ||
Если <math>i = n</math>, то конец, иначе возврат к п.1. | Если <math>i = n</math>, то конец, иначе возврат к п.1. | ||
| − | === | + | === Serial complexity of the algorithm === |
Для разложения трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в последовательном варианте требуется: | Для разложения трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в последовательном варианте требуется: | ||
| Line 74: | Line 75: | ||
При классификации по последовательной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам ''с линейной сложностью''. | При классификации по последовательной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам ''с линейной сложностью''. | ||
| − | === | + | === Information graph === |
| + | |||
<div class="thumb"> | <div class="thumb"> | ||
<div class="thumbinner" style="width:{{#expr: 2 * (500 + 35) + 3 * (3 - 1) + 8}}px"> | <div class="thumbinner" style="width:{{#expr: 2 * (500 + 35) + 3 * (3 - 1) + 8}}px"> | ||
| Line 86: | Line 88: | ||
Как видно из рис.1, на котором одна из операций разложена на 2 составляющие, информационный граф является чисто последовательным. | Как видно из рис.1, на котором одна из операций разложена на 2 составляющие, информационный граф является чисто последовательным. | ||
| − | === | + | === Parallelization resource of the algorithm === |
При разложении трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в требуется выполнить: | При разложении трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в требуется выполнить: | ||
| Line 96: | Line 98: | ||
В каждом ярусе - ровно по одной операции. При классификации по параллельной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам ''с линейной сложностью''. Ширина ярусов везде равна 1, и, таким образом, весь алгоритм представляет собой сплошное "узкое место". | В каждом ярусе - ровно по одной операции. При классификации по параллельной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам ''с линейной сложностью''. Ширина ярусов везде равна 1, и, таким образом, весь алгоритм представляет собой сплошное "узкое место". | ||
| − | === | + | === Input and output data of the algorithm === |
'''Входные данные''': трёхдиагональная матрица <math>A</math> (элементы <math>a_{ij}</math>). | '''Входные данные''': трёхдиагональная матрица <math>A</math> (элементы <math>a_{ij}</math>). | ||
| Line 106: | Line 108: | ||
'''Объём выходных данных''': формально <math>3n-2</math>. Однако благодаря совпадению <math>n</math> входных и выходных данных реально вычисляется лишь <math>2n-2</math> элементов. | '''Объём выходных данных''': формально <math>3n-2</math>. Однако благодаря совпадению <math>n</math> входных и выходных данных реально вычисляется лишь <math>2n-2</math> элементов. | ||
| − | === | + | === Properties of the algorithm === |
Соотношение последовательной и параллельной сложности в случае любых ресурсов, как хорошо видно, является '''единицей''' (алгоритм не является распараллеливаемым). | Соотношение последовательной и параллельной сложности в случае любых ресурсов, как хорошо видно, является '''единицей''' (алгоритм не является распараллеливаемым). | ||
| Line 119: | Line 121: | ||
</math> | </math> | ||
| − | == | + | == Software implementation of the algorithm == |
| − | === | + | |
| + | === Implementation peculiarities of the serial algorithm === | ||
В простейшем варианте алгоритм на Фортране можно записать так: | В простейшем варианте алгоритм на Фортране можно записать так: | ||
| Line 142: | Line 145: | ||
Элементы A(1,N) и A(3,N) при данном способе хранения не адресуются. | Элементы A(1,N) и A(3,N) при данном способе хранения не адресуются. | ||
| − | === | + | === Locality of data and computations === |
По приведённым фрагментам программ видно, что степень локальности данных и вычислений очень высока. Особенно это выражено для второго варианта, в котором все данные, как используемые операцией, так и вычисляемые ей, хранятся и используются "рядом". Однако выигрыш от столь высокой локальности, однако, ограничен тем, что каждое перевычисляемое данное используется затем только однажды. Это вызвано простой причиной: количество обрабатываемых алгоритмом данных, как уже описано выше, равно количеству арифметических операций. | По приведённым фрагментам программ видно, что степень локальности данных и вычислений очень высока. Особенно это выражено для второго варианта, в котором все данные, как используемые операцией, так и вычисляемые ей, хранятся и используются "рядом". Однако выигрыш от столь высокой локальности, однако, ограничен тем, что каждое перевычисляемое данное используется затем только однажды. Это вызвано простой причиной: количество обрабатываемых алгоритмом данных, как уже описано выше, равно количеству арифметических операций. | ||
| − | === | + | === Possible methods and considerations for parallel implementation of the algorithm === |
Компактная схема метода Гаусса в применении к разложению трёхдиагональной матрицы - это чисто последовательный алгоритм. Его невозможно исполнять параллельно из-за того, что каждая из операций требует в качестве данных результат предыдущей и сама, в свою очередь, отдаёт результат как входное данное для следующей. | Компактная схема метода Гаусса в применении к разложению трёхдиагональной матрицы - это чисто последовательный алгоритм. Его невозможно исполнять параллельно из-за того, что каждая из операций требует в качестве данных результат предыдущей и сама, в свою очередь, отдаёт результат как входное данное для следующей. | ||
| Line 154: | Line 157: | ||
Кроме этого, возможен случай, когда нужны многие разложения разных трёхдиагональных матриц, тогда этот последовательный алгоритм может быть параллельно выполнен для этих матриц на разных узлах вычислительной системы. | Кроме этого, возможен случай, когда нужны многие разложения разных трёхдиагональных матриц, тогда этот последовательный алгоритм может быть параллельно выполнен для этих матриц на разных узлах вычислительной системы. | ||
| − | === | + | === Scalability of the algorithm and its implementations === |
При чисто последовательном характере алгоритма его ресурсы параллельности полностью отсутствуют: выгоднее все вычисления проводить на одном процессоре. | При чисто последовательном характере алгоритма его ресурсы параллельности полностью отсутствуют: выгоднее все вычисления проводить на одном процессоре. | ||
| − | === | + | === Dynamic characteristics and efficiency of the algorithm implementation === |
| − | === | + | === Conclusions for different classes of computer architecture === |
Из-за последовательной структуры более или менее эффективно алгоритм в своём неизменном виде может быть выполнен только на вычислителе классической фон-неймановской архитектуры. | Из-за последовательной структуры более или менее эффективно алгоритм в своём неизменном виде может быть выполнен только на вычислителе классической фон-неймановской архитектуры. | ||
| − | === | + | === Existing implementations of the algorithm === |
| − | |||
| − | |||
| + | == References == | ||
<references /> | <references /> | ||
Revision as of 14:32, 2 March 2018
| Gaussian elimination, compact scheme for tridiagonal matrices, serial variant | |
| Sequential algorithm | |
| Serial complexity | [math]3n-3[/math] |
| Input data | [math]3n-2[/math] |
| Output data | [math]3n-2[/math] |
| Parallel algorithm | |
| Parallel form height | [math]3n-3[/math] |
| Parallel form width | [math]1[/math] |
Main authors: Alexey Frolov
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Компактная схема метода Гаусса для трёхдиагональной матрицы[1][2] вычисляет такое [math]LU[/math]-разложение трёхдиагональной матрицы
- [math] A = \begin{bmatrix} a_{11} & a_{12} & 0 & \cdots & \cdots & 0 \\ a_{21} & a_{22} & a_{23}& \cdots & \cdots & 0 \\ 0 & a_{32} & a_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & a_{n-1 n-2} & a_{n-1 n-1} & a_{n-1 n} \\ 0 & \cdots & \cdots & 0 & a_{n n-1} & a_{n n} \\ \end{bmatrix} [/math]
на две двухдиагональные:
- [math] L = \begin{bmatrix} 1 & 0 & 0 & \cdots & \cdots & 0 \\ l_{21} & 1 & 0 & \cdots & \cdots & 0 \\ 0 & l_{32} & 1 & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & l_{n-1 n-2} & 1 & 0 \\ 0 & \cdots & \cdots & 0 & l_{n n-1} & 1 \\ \end{bmatrix} [/math]
и
- [math] U = \begin{bmatrix} u_{11} & u_{12} & 0 & \cdots & \cdots & 0 \\ 0 & u_{22} & u_{23}& \cdots & \cdots & 0 \\ 0 & 0 & u_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & u_{n-1 n-1} & u_{n-1 n} \\ 0 & \cdots & \cdots & 0 & 0 & u_{n n} \\ \end{bmatrix} [/math].
При такой фиксации диагонали матрицы [math]L[/math] все элементы разложения становятся строго предопределёнными, с точностью до ошибок округления. Компактная схема даёт естественные формулы нахождения остальных элементов получающихся двухдиагональных матриц. [math]LU[/math]-разложение трёхдиагональной матрицы является частным случаем для компактной схемы метода Гаусса общего вида, однако из-за специфики матрицы характеристики алгоритма кардинально меняются по сравнению с компактной схемой для плотных матриц.
1.2 Mathematical description of the algorithm
Формулы алгоритма следующие:
[math]u_{11} = a_{11} [/math]
[math]u_{i i+1} = a_{i i+1}, \quad i \in [1, n-1] [/math]
[math]l_{i+1 i} = a_{i+1 i} / u_{i i} , \quad i \in [1, n-1] [/math]
[math]u_{ii} = a_{ii} - l_{i i-1} u_{i-1 i}, \quad i \in [2, n] [/math]
1.3 Computational kernel of the algorithm
Как видно из формул, n-1 раз повторяется одна и та же последовательность трёх операций: деление, умножение, вычитание.
1.4 Macro structure of the algorithm
В качестве макровершины можно взять последовательность трёх операций: деление, умножение, вычитание. Эти макровершины выполняются в алгоритме n-1 раз.
1.5 Implementation scheme of the serial algorithm
В схеме учтено, что ряд выходных данных вычислять не нужно - они совпадают с входными. В частности,
[math]u_{11} = a_{11} [/math]
[math]u_{i i+1} = a_{i i+1}, \quad i \in [1, n-1][/math].
В начале процесса [math]i = 1[/math]
1. Вычисляется [math]l_{i+1 i} = a_{i+1 i} / u_{i i}[/math]
[math]i[/math] увеличивается на 1
2. Вычисляется [math]u_{ii} = a_{ii} - l_{i i-1} u_{i-1 i}[/math]
Если [math]i = n[/math], то конец, иначе возврат к п.1.
1.6 Serial complexity of the algorithm
Для разложения трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в последовательном варианте требуется:
- [math]n-1[/math] делений,
- [math]n-1[/math] умножений,
- [math]n-1[/math] сложений (вычитаний).
При классификации по последовательной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам с линейной сложностью.
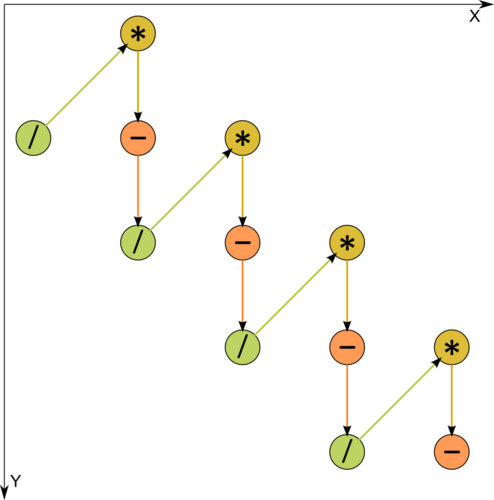
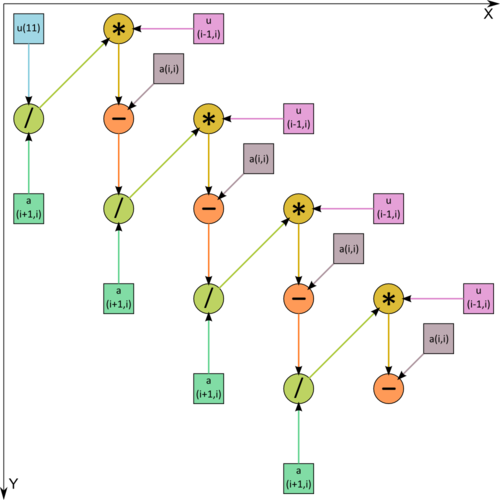
1.7 Information graph
Как видно из рис.1, на котором одна из операций разложена на 2 составляющие, информационный граф является чисто последовательным.
1.8 Parallelization resource of the algorithm
При разложении трёхдиагональной матрицы порядка n компактной схемой метода Гаусса в требуется выполнить:
- [math]n-1[/math] ярусов делений,
- [math]n-1[/math] ярусов умножений,
- [math]n-1[/math] ярусов сложений (вычитаний).
В каждом ярусе - ровно по одной операции. При классификации по параллельной сложности, таким образом, компактная схема метода Гаусса для разложения трёхдиагональной матрицы в последовательном варианте относится к алгоритмам с линейной сложностью. Ширина ярусов везде равна 1, и, таким образом, весь алгоритм представляет собой сплошное "узкое место".
1.9 Input and output data of the algorithm
Входные данные: трёхдиагональная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).
Объём входных данных: [math]3n-2[/math]. В разных реализациях размещение для экономии хранения может быть выполнено разным образом. Например, каждая диагональ может быть строкой массива.
Выходные данные: нижняя двухдиагональная матрица [math]L[/math] (элементы [math]l_{ij}[/math], причём [math]l_{ii}=1[/math]) и верхняя двухдиагональная матрица [math]U[/math] (элементы [math]u_{ij}[/math]).
Объём выходных данных: формально [math]3n-2[/math]. Однако благодаря совпадению [math]n[/math] входных и выходных данных реально вычисляется лишь [math]2n-2[/math] элементов.
1.10 Properties of the algorithm
Соотношение последовательной и параллельной сложности в случае любых ресурсов, как хорошо видно, является единицей (алгоритм не является распараллеливаемым).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь константа (арифметических операций столько же, сколько данных).
Описываемый алгоритм является полностью детерминированным.
Эквивалентное возмущение [math]M[/math] у алгоритма не более возмущения [math]\delta A[/math], вносимому в матрицу при вводе чисел в компьютер: [math] ||M||_{E} \leq ||\delta A||_{E} [/math]
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
В простейшем варианте алгоритм на Фортране можно записать так:
DO I = 1, N-1
A(I+1,I) = A(I+1,I)/A(I,I)
A(I+1,I+1) = A(I+1,I+1) - A(I+1,I)*A(I,I+1)
END DO
Разложение размещается там же, где размещалась исходная матрица. Индексация такая же как и для плотной матрицы.
Однако чаще трёхдиагональную матрицу, естественно, хранят более экономно. Например, если диагонали нумеруются слева направо и каждая хранится в одной строке массива, то получается такая версия:
DO I = 1, N-1
A(1,I) = A(1,I)/A(2,I)
A(2,I+1) = A(2,I+1) - A(1,I)*A(3,I)
END DO
в которой разложение также сохраняется на месте исходных данных. Элементы A(1,N) и A(3,N) при данном способе хранения не адресуются.
2.2 Locality of data and computations
По приведённым фрагментам программ видно, что степень локальности данных и вычислений очень высока. Особенно это выражено для второго варианта, в котором все данные, как используемые операцией, так и вычисляемые ей, хранятся и используются "рядом". Однако выигрыш от столь высокой локальности, однако, ограничен тем, что каждое перевычисляемое данное используется затем только однажды. Это вызвано простой причиной: количество обрабатываемых алгоритмом данных, как уже описано выше, равно количеству арифметических операций.
2.3 Possible methods and considerations for parallel implementation of the algorithm
Компактная схема метода Гаусса в применении к разложению трёхдиагональной матрицы - это чисто последовательный алгоритм. Его невозможно исполнять параллельно из-за того, что каждая из операций требует в качестве данных результат предыдущей и сама, в свою очередь, отдаёт результат как входное данное для следующей.
Варианты распараллеливания компактной схемы метода Гаусса для трёхдиагональной матрицы используют ассоциативность операций, и, следовательно, представляют собой совсем другие алгоритмы, которые можно изучить на соответствующей странице.
Кроме этого, возможен случай, когда нужны многие разложения разных трёхдиагональных матриц, тогда этот последовательный алгоритм может быть параллельно выполнен для этих матриц на разных узлах вычислительной системы.
2.4 Scalability of the algorithm and its implementations
При чисто последовательном характере алгоритма его ресурсы параллельности полностью отсутствуют: выгоднее все вычисления проводить на одном процессоре.
2.5 Dynamic characteristics and efficiency of the algorithm implementation
2.6 Conclusions for different classes of computer architecture
Из-за последовательной структуры более или менее эффективно алгоритм в своём неизменном виде может быть выполнен только на вычислителе классической фон-неймановской архитектуры.
2.7 Existing implementations of the algorithm
3 References
Категория:Алгоритмы с низким уровнем параллелизма Категория:Разложения матриц Категория:Решение систем линейных уравнений