User:GrishinaAnna/Метод Якоби вычисления сингулярных чисел и векторов

From AlgowikiPool
Jump to navigation Jump to search

Авторы статьи: Гришина Анна (группа 604), Наталия Чудновская (группа 611)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Якоби позволяет получить разложение произвольной матрицы [math]G[/math] размера [math]n[/math]×[math]n[/math] в виде [math]G=USV^*[/math], где [math]U[/math] и [math]V[/math] — унитарные матрицы, [math]S[/math] — диагональная матрица с вещественными положительными числами на диагонали. Диагональные элементы матрицы называются сингулярными числами матрицы [math]G[/math], а столбцы матриц и левыми и правыми сингулярными векторами соответственно.

В основе метода лежит утверждение о том, что собственными значениями симметричной матрицы [math]G^TG[/math] являются квадраты сингулярных чисел, а соответствующие ортонормированные собственные векторы – правыми сингулярными векторами. Для вычисления собственных значений и собственных векторов симметричной матрицы [math]G^TG[/math] используется метод односторонних вращений (неявный метод Якоби), на каждом шаге которого вычисляется вращение Якоби [math]J[/math]. С его помощью матрица [math]G^TG[/math] неявно пересчитывается в [math]J^TG^TGJ[/math]. Вращение выбрано так, чтобы пара внедиагональных элементов из [math]G^TG[/math] обратилась в нуль в матрице [math]J^TG^TGJ[/math]. Однако, ни [math]G^TG[/math], ни [math]J^TG^TGJ[/math] не вычисляются в явном виде; вместо них вычисляется матрица [math]GJ[/math], которая подается на вход на следующем шаге алгоритма. Алгоритм выполняется, пока [math]G^TG[/math] не станет достаточно близка к диагональной матрице, после чего вычисляются собственные числа матрицы [math]G[/math], полученной на последнем шаге, которые принимаются за сингулярные числа. Правые сингулярные векторы получаются в результате накопления произведений вращений Якоби.

Метод Якоби для вычисления сингулярных значений и векторов является самым медленным из имеющихся, но тем не менее, интерес к нему сохраняется, потому что для некоторых типов матриц [math]G[/math] он способен вычислять числа и сингулярные векторы намного точнее, чем другие методы. Так, например, метод Якоби вычисляет сингулярные числа матрицы [math]G[/math] с высокой точностью, если [math]G[/math] может быть представлена в виде [math]G=DX[/math], где [math]D[/math] – диагональная матрица, а [math]X[/math] – хорошо обусловлена. Выигрыш метода Якоби в этом случае перед другими алгоритмами объясняется следующим образом: в методе Якоби заданная матрица обрабатывается без предварительного приведения к двухдиагональному виду, в то время как другие алгоритмы включают в себя приведение матрицы к двухдиагональной форме, из-за чего и теряют все верные разряды во всех сингулярных числах, кроме старшего.

Следует иметь в виду, что метод Якоби эффективен при не очень больших размерах матрицы – максимум до [math]n[/math] ~ [math]100[/math]. Дело не только в том, что метод не будет сходиться за конечное время, дело еще и в излишне большом количестве операций, которое приведет к ошибкам округления и потере точности.

1.2 Математическое описание алгоритма

Исходные данные: матрица [math]G[/math] размера [math]n[/math]×[math]n[/math].

Вычисляемые данные: Матрица [math]S=[/math]diag([math]\sigma_{i}[/math]), где [math]\sigma_{i}[/math] - сингулярные числа, матрица [math]U[/math] левых сингулярных векторов и матрица [math]V[/math] правых сингулярных векторов.

Описание используемой в алгоритме процедуры одностороннего вращения входной матрицы [math]G[/math] One-Sided-Jacobi-Rotation [math](G, j, k)[/math]: 

proc One-Sided-Jacobi-Rotation [math](G,j,k)[/math]
    вычислить [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math]
    if [math]|a_{jk}|[/math] не слишком мал
        [math]
         \begin{align}
         \tau &= {a_{jj} - a_{kk}}/{2a_{jk}} \\
         t &= {sign(\tau)}/(|\tau| + \sqrt{1 + \tau^2}) \\
         c &= 1/(\sqrt{1 + t^2}) \\
         s &= ct \\
         G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}[/math]
        if нужны правые сингулярные векторы 
            [math]J = JR(j,k,\theta)[/math]
        end if
    end if

Где [math]R(j,k,\theta)[/math] – матрица вращения Якоби, которая выбирается так, чтобы обнулить пару внедиагональных элементов.

[math]R(j,k,\theta) =\begin{pmatrix} 1 & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ \0 & \cos (\theta) & \sin(\theta) & 0 \end{pmatrix} [/math]

1.3 Информационный граф

Построим информационный граф отдельно для процедуры вращения, а затем для всего алгоритма с обращениями к процедуре вращения. Для процедуры вращения в качестве узлов графа выберем точки на равномерной сетке [math]2xN[/math], где [math]N[/math] – размерность матрицы. Для вычисления коэффициентов в матрице поворота требуется вычислить значения [math]a_{ii}, a_{ji}, a_{jj}[/math] матрицы [math]G^TG[/math]. После того, как посчитаны коэффициенты, необходимо пересчитать значения в [math]i[/math] и [math]j[/math] столбцах матрицы. Эти значения зависят от входных значений соответствующих элементов и рассчитанных ранее значений [math]\cos (\theta)[/math] и [math]\sin(\theta)[/math].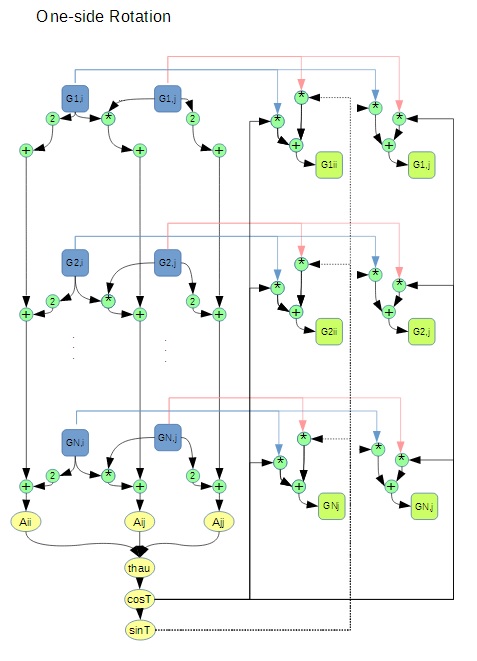Graf 1 chudnovskaya.jpg

Далее рассмотрим информационный граф для всего алгоритма. Как было показано ранее, процедура вращения в плоскости [math](i,j)[/math] зависит только от столбцов [math](i,j)[/math] матрицы [math]G[/math] и рассчитывает новые значения только для [math]i[/math] и [math]j[/math] столбцов, причем новое значение вычисляется для каждого элемента в столбце. С учетом сказанного выше будем строить граф вычислений, рассматривая каждый столбец матрицы G как многомерную переменную и введя обозначение [math]G(:,i)[/math] для [math]i[/math]-го столбца. В зависимости от порядка перебора пар элементов возможны различные графы, параллельные по данным в большей и меньшей степени. При простом переборе for i=1:N; for j=1:N; calc(i,j); end Для каждого последующего элемента требуется столбец из предыдущего внутреннего цикла. С другой стороны, как было показано ранее, процедура односторонних вращений зависит и изменяет только [math]i[/math] и [math]j[/math] столбцы. Таким образом пары [math](i1,j1)[/math] И [math](i_2,j_2)[/math] такие, что все [math]i_1,i_2,j_1,j_2[/math] – различны можно вычислять независимо.File:Graf 3 chudnovskaya.jpg

Одним из вариантов реализации такого подхода является следующий. Будем строить пары [math](i,j)[/math] специального вида:

Retrieved from "https://algowiki-project.org/algowiki/pool/index.php?title=User:GrishinaAnna/Метод_Якоби_вычисления_сингулярных_чисел_и_векторов&oldid=486"