User:GrishinaAnna/Метод Якоби вычисления сингулярных чисел и векторов

Авторы статьи: Гришина Анна (группа 604), Наталия Чудновская (группа 611)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Якоби позволяет получить разложение произвольной матрицы [math]G[/math] размера [math]n[/math]×[math]n[/math] в виде [math]G=USV^*[/math], где [math]U[/math] и [math]V[/math] — унитарные матрицы, [math]S[/math] — диагональная матрица с вещественными положительными числами на диагонали. Диагональные элементы матрицы называются сингулярными числами матрицы [math]G[/math], а столбцы матриц и левыми и правыми сингулярными векторами соответственно.

В основе метода лежит утверждение о том, что собственными значениями симметричной матрицы [math]G^TG[/math] являются квадраты сингулярных чисел, а соответствующие ортонормированные собственные векторы – правыми сингулярными векторами. Для вычисления собственных значений и собственных векторов симметричной матрицы [math]G^TG[/math] используется метод односторонних вращений (неявный метод Якоби), на каждом шаге которого вычисляется вращение Якоби [math]J[/math]. С его помощью матрица [math]G^TG[/math] неявно пересчитывается в [math]J^TG^TGJ[/math]. Вращение выбрано так, чтобы пара внедиагональных элементов из [math]G^TG[/math] обратилась в нуль в матрице [math]J^TG^TGJ[/math]. Однако, ни [math]G^TG[/math], ни [math]J^TG^TGJ[/math] не вычисляются в явном виде; вместо них вычисляется матрица [math]GJ[/math], которая подается на вход на следующем шаге алгоритма. Алгоритм выполняется, пока [math]G^TG[/math] не станет достаточно близка к диагональной матрице, после чего вычисляются собственные числа матрицы [math]G[/math], полученной на последнем шаге, которые принимаются за сингулярные числа. Правые сингулярные векторы получаются в результате накопления произведений вращений Якоби.

Метод Якоби для вычисления сингулярных значений и векторов является самым медленным из имеющихся, но тем не менее, интерес к нему сохраняется, потому что для некоторых типов матриц [math]G[/math] он способен вычислять числа и сингулярные векторы намного точнее, чем другие методы. Так, например, метод Якоби вычисляет сингулярные числа матрицы [math]G[/math] с высокой точностью, если [math]G[/math] может быть представлена в виде [math]G=DX[/math], где [math]D[/math] – диагональная матрица, а [math]X[/math] – хорошо обусловлена. Выигрыш метода Якоби в этом случае перед другими алгоритмами объясняется следующим образом: в методе Якоби заданная матрица обрабатывается без предварительного приведения к двухдиагональному виду, в то время как другие алгоритмы включают в себя приведение матрицы к двухдиагональной форме, из-за чего и теряют все верные разряды во всех сингулярных числах, кроме старшего.

Следует иметь в виду, что метод Якоби эффективен при не очень больших размерах матрицы – максимум до [math]n[/math] ~ [math]100[/math]. Дело не только в том, что метод не будет сходиться за конечное время, дело еще и в излишне большом количестве операций, которое приведет к ошибкам округления и потере точности.

1.2 Математическое описание алгоритма

Исходные данные: матрица [math]G[/math] размера [math]n[/math]×[math]n[/math].

Вычисляемые данные: Матрица [math]S = diag(\sigma_{i})[/math], где [math]\sigma_{i}[/math] - сингулярные числа, матрица [math]U[/math] левых сингулярных векторов и матрица [math]V[/math] правых сингулярных векторов.

Описание используемой в алгоритме процедуры одностороннего вращения входной матрицы [math]G[/math] One-Sided-Jacobi-Rotation [math](G, j, k)[/math]:

proc One-Sided-Jacobi-Rotation [math](G,j,k)[/math]
    вычислить [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math]
    if [math]|a_{jk}|[/math] не слишком мал
        [math]
         \begin{align}
         \tau &= {a_{jj} - a_{kk}}/{2a_{jk}} \\
         t &= {sign(\tau)}/(|\tau| + \sqrt{1 + \tau^2}) \\
         c &= 1/(\sqrt{1 + t^2}) \\
         s &= ct \\
         G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}[/math]
        if нужны правые сингулярные векторы 
            [math]J = JR(j,k,\theta)[/math]
        end if
    end if

Где [math]R(j,k,\theta)[/math] – матрица вращения Якоби, которая выбирается так, чтобы обнулить пару внедиагональных элементов.

[math] J_i = R(j,k,\theta) = \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix} [/math] [math] \begin{bmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{bmatrix} [/math]

Метод односторонних вращений (основной алгоритм):

Для всех недиагональных элементов матрицы [math](G^TG)^{(i)} = A^{(i)}[/math] подряд, т.е. [math](A_{12}^{(i)}, A_{13}^{(i)},\dots, A_{1n}^{(i)}, A_{23}^{(i)}, A_{24}^{(i)},\dots, A_{2n}^{(i)},\dots, A_{n-1n}^{(i)})[/math] проделывать следующее:

Если [math]|A_{jk}^{(i)}| \lt = \epsilon [/math], то переходим к следующему элементу.

Если [math]|A_{jk}^{(i)}| \gt \epsilon [/math], то выполняем вращение в плоскости [math](jk)[/math], т.е. вызываем процедуру One-Sided-Jacobi-Rotation [math](G, j, k)[/math], после чего переходим к началу алгоритма.

Если при очередном проходе всей матрицы ни одного вращения не было, то алгоритм переходит непосредственно к вычислению искомых значений:

При каждом элементарном вращении в плоскости [math](jk)[/math] сумма квадратов модулей начальных элементов убывает в точности на [math]2 |A_{jk}^{(i)}|^2[/math]. Однако элементы [math]|A_{jk}^{(i)}|[/math], приведенные к нулю на [math]i[/math]-й итерации, на последующей итерации немного возрастают. При [math]i \to \inf[/math] получается монотонно убывающая ограниченная снизу нулем последовательность . Это и означает сходимость метода, причем [math] A(i) \to S = diag(\sigma_{1}, \dots, \sigma_{n}) [/math]

1.3 Вычислительное ядро алгоритма

Основную сложность в алгоритме представляет многократное обращение к процедуре One-Sided-Jacobi-Rotation, сложность которой составляет [math]O(n)[/math] (см. раздел Макроструктура алгоритма). Всего таких обращений по меньшей мере [math]\frac{n^2-n}{2}[/math], т.к. процедура должна сработать как минимум один раз для каждого наддиагонального элемента, чтобы его обнулить. Также серьезную сложность представляет вычисление [math](G^TG)[/math] на каждом шаге, сложность которого составляет [math]O(n^3)[/math]. Основная проблема заключается в том, что обнуленный на шаге [math](i)[/math] элемент может снова стать ненулевым на шаге [math](i+1)[/math]. Из-за этого число необходимых вращений изначально недетерминировано.

1.4 Макроструктура алгоритма

Рассмотрим подробно схему работы, а также вычислительную сложность процедуры One-Sided-Jacobi-Rotation [math](G, j, k)[/math].

1) Вычисление [math]A_{jj} = (G^TG)_{jj}[/math] требует [math]n[/math] операций умножения и [math]n-1[/math] операцию сложения (т.к. нет необходимости явно вычислять произведение двух матриц). Столько же операций нужно и для вычисления [math]A_{jk}[/math] и [math]A_{kk}[/math]. То есть, всего [math]3n[/math] операций умножения и [math]3n-3[/math] операции сложения на первом шаге.

2) Вычисления [math]\tau, t, c, s[/math] не представляют значимой вычислительной сложности.

3) Заметим, что матрица [math]J[/math] отличается от единичной лишь в [math]4[/math] элементах. Это значит, что в матрице [math]GJ[/math] все столбцы, кроме двух, будут совпадать со столбцами матрицы [math]G[/math]. А для вычисления двух новых столбцов, при учете вида матрицы [math]J[/math], достаточно [math]4n[/math] операций умножения и [math]2n[/math] сложений. Аналогичное число операций требуется и для вычисления произведения [math]JR(j,k,\theta)[/math].

4) Итого, процедура One-Sided-Jacobi-Rotation [math](G, j, k)[/math] требует порядка [math]O(n)[/math] операций.

В качестве следующей макрооперации можно выделить вычисление [math]G^TG[/math] на каждом шаге алгоритма.

После выполнения алгоритма односторонних вращений, когда матрица [math]G^TG[/math] станет достаточно близка к диагональной, необходимо вычислить искомые матрицы [math]S, U, V [/math].

1) [math]\sigma_{i} = ||G(:, i)||_{2}[/math], т.е. для вычисления [math]\sigma_{i}[/math] потребуется [math]n[/math] операций умножения, а для вычисления [math]S = diag(\sigma_{i})[/math] -- [math]O(n^2)[/math] операций.

2) [math]U = [u_{1},\dots, u_{n}][/math], где [math]u_{i} = G(:, i)/ \sigma_{i}[/math]. Значит, вычисление [math]U[/math] потребует [math]O(n^2)[/math] операций.

3) Матрица [math]V[/math] правых сингулярных векторов формируется в ходе работы алгоритма: [math]V = J[/math]

1.5 Схема реализации последовательного алгоритма

Схема реализации последовательного алгоритма подробно описана в разделе Математическое описание алгоритма

1.6 Последовательная сложность алгоритма

На каждом шаге алгоритма вычисляется [math](G^TG)[/math] и вызывается процедура вращения. Сложность первого вычисления [math]O(n^3)[/math], а второго – [math]O(n)[/math]. Т.е. общая сложность шага алгоритма равна [math]O(n^3)[/math].

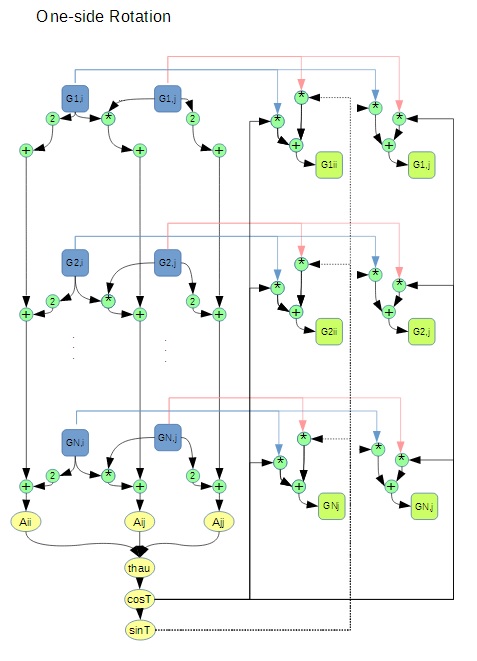
1.7 Информационный граф

Построим информационный граф отдельно для процедуры вращения, а затем для всего алгоритма с обращениями к процедуре вращения.

Для процедуры вращения в качестве узлов графа выберем точки на равномерной сетке [math]2[/math]×[math]n[/math], где [math]n[/math] – размерность матрицы. Для вычисления коэффициентов в матрице поворота требуется вычислить значения [math]a_{ii}, a_{ji}, a_{jj}[/math] матрицы [math]G^TG[/math].

После того как посчитаны коэффициенты, необходимо пересчитать значения в [math]i[/math] и [math]j[/math] столбцах матрицы. Эти значения зависят от входных значений соответствующих элементов и рассчитанных ранее [math]\cos (\theta)[/math] и [math]\sin(\theta)[/math].

Граф выглядит следующим образом:

Рассмотрим информационный граф для всего алгоритма.

Как было показано ранее, процедура вращения в плоскости [math](i,j)[/math] зависит только от столбцов [math](i,j)[/math] матрицы [math]G[/math] и рассчитывает новые значения только для [math]i[/math] и [math]j[/math] столбцов, причем новое значение вычисляется для каждого элемента в столбце. С учетом сказанного выше будем строить граф вычислений, рассматривая каждый столбец матрицы G как многомерную переменную и введя обозначение [math]G(:,i)[/math] для [math]i[/math]-го столбца.

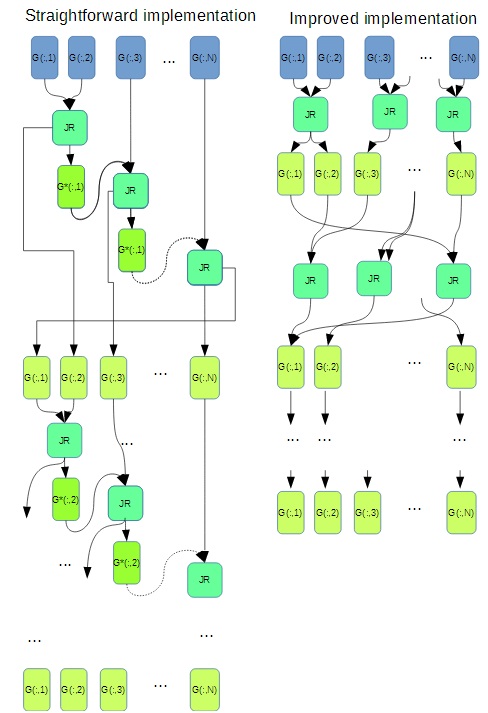
В зависимости от порядка перебора пар элементов возможны различные графы, параллельные по данным в большей и меньшей степени.

Рассмотрим следующий простой перебор:

     for [math]i=1:n;[/math]
         for [math]j=1:n;[/math]
             calculate[math](i,j);[/math]
     end;

При таком переборе для каждого последующего элемента требуется столбец из предыдущего внутреннего цикла.

С другой стороны, как было показано ранее, процедура односторонних вращений зависит и изменяет только [math]i[/math] и [math]j[/math] столбцы. Таким образом пары [math](i_1,j_1)[/math] И [math](i_2,j_2)[/math] такие, что все [math]i_1,i_2,j_1,j_2[/math] – различны можно вычислять независимо.

Одним из вариантов реализации такого подхода является следующий. Будем строить пары [math](i,j)[/math] специального вида:тут большая хрень которую надо перепечатать

1.8 Ресурс параллелизма

Рассмотрим ресурс параллелизма внутри процедуры вращений.

На каждом из n ярусов требуется выполнить 3 умножения, которые могут быть произведены параллельно. Обратим внимание, что сложения тоже могут быть выполнены параллельно с учетом ассоциативности операции и с применением редукции.

Далее для вычисления обновленных столбцов матрицы на каждом из [math]n[/math] ярусов в правой группе вершин требуется выполнить 4 умножения и 2 сложения. Все ярусы могут быть вычислены параллельно.

Рассмотрим возможность параллельного вычисления на более высоком уровне. Как было показано ранее, можно рассматривать столбцы матрицы как многомерные переменные.

При простом переборе, изображенном на графе слева, данные каждый раз зависят от предыдущих вычислений, однако, как было сказано ранее, при изменении порядка перебора возникает возможность параллельного вычисления вращений. При использовании указанной в разделе 1.7 схеме параллельно могут вычисляться [math]n/2[/math] пар.

1.9 Входные и выходные данные

Входные данные: матрица [math]G[/math] размера [math]n[/math]×[math]n[/math].

Объем входных данных: [math]n^2[/math].

Выходные данные: диагональная матрица [math]S[/math], диагональными элементами которой являются сингулярные числа, матрицы [math]U[/math] и [math]V[/math] левых и правых сингулярных векторов.

Объем выходных данных: [math]2n^2+n[/math]

1.10 Свойства алгоритма

Пусть [math]G = DX[/math] - матрица порядка [math]n[/math], причем [math]D[/math] и [math]X[/math] невырожденны и [math]D[/math] - диагональная матрица.

Пусть [math]\tilde{G}[/math] - матрица, полученная из [math]G[/math] в результате m-кратного обращения к процедуре One-Sided-Jacobi-Rotation[math](G,j,k)[/math] в арифметике с плавающей точкой. Обозначим через [math]\sigma_{1} \geq \ldots \geq \sigma_{n}[/math] и [math]\tilde{\sigma_{1}} \geq \ldots \geq \tilde{\sigma_{n}}[/math] сингулярные числа матриц [math]G[/math] и [math]\tilde{G}[/math]. Тогда

[math]\frac{\vert\sigma_{i}-\tilde{\sigma_{i}}\vert}{\sigma_{i}} \leq O(m\varepsilon)\kappa(X)[/math],

где [math]\kappa(X)=\Vert X \Vert \cdot \Vert X^{-1} \Vert[/math] есть число обусловленности матрицы [math]X[/math].

Другими словами, относительная погрешность вычисленных сингулярных чисел мала, если мало число обусловленности матрицы [math]X[/math].

3 Литература

1. Дж. Деммель Вычислительная линейная алгебра. Изд. Мир, 2001.