Участник:Danyanya/Алгоритм Ланцоша для точной арифметики (без переортогонализации)
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Konshin и ASA. |
| Алгоритм Ланцоша для точной арифметики (без переортогонализации) | |
| Последовательный алгоритм | |
| Последовательная сложность | O(kn^2) |
| Объём входных данных | \frac{n(n + 1)}{2} |
| Объём выходных данных | k(n + 1) |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(k \log(n)) |
| Ширина ярусно-параллельной формы | O(n^2) |
Основные авторы описания: Д.Р.Слюсарь (1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 2.4, 2.7), М.А.Григорьев (1.2, 1.7, 1.8, 1.9, 2.4, 2.7, 3)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Ланцоша поиска собственных значений был опубликован Корнелием Ланцошем в 1950 году [1]. Этот итерационный алгоритм применим только к эрмитовым матрицам A. Метод позволяет за k итераций вычислять k-ое приближение собственных значений и собственных векторов исходной матрицы A.
В данной статье рассмотрен упрощенный вариант алгоритма Ланцоша, подразумевающий отсутствие влияния ошибок округления на вычислительный процесс.
Данный алгоритм является неустойчивым, вследствие чего на практике применяется модифицированный алгоритм Ланцоша с полной переортогонализацией предложенный в 1970 Ojalvo и Newman[2].
1.2 Математическое описание алгоритма
На вход алгоритма подается эрмитова матрица A = A^\dagger (в вещественном случае матрица симметрична) ,
- A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1\ n-1} & a_{1\ n} \\ a_{12} & a_{22} & a_{23} & \cdots & a_{2\ n-1} & a_{2\ n} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{3\ n-1} & a_{3\ n} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ a_{1\ n-1} & \cdots & \cdots & a_{n-2\ n-1} & a_{n-1\ n-1} & a_{n-1\ n} \\ a_{1\ n} & \cdots & \cdots & a_{n-2\ n} & a_{n-1\ n} & a_{n\ n} \\ \end{pmatrix}
Алгоритм Ланцоша соединяет в себя метод Ланцоша построения крыловского подпространства с процедурой Релея-Ритца[1]. Иными словами, из оргонормированных векторов Ланцоша [3] на каждой итерации строится матрица Q_k = [q_1, q_2, \dots, q_k] размерности n \times k. В качестве приближенных собственных значений матрицы A берутся числа Ритца, т.е. собственные значения симметричной трехдиагональной матрицы T_k = Q^T_k A Q:
T_k = \begin{pmatrix} \alpha_1 & \beta_1 & 0 & \dots & 0 \\ \beta_1 & \alpha_2 & \beta_2 & \dots & 0 \\ 0 & \beta_2 & \ddots & \ddots & \vdots \\ \vdots & \vdots & \ddots & \ddots & \beta_{k-1} \\ 0 & \dots & \dots & \beta_{k-1} & \alpha_k \end{pmatrix}
На выходе алгоритма получается собственные векторы и вектор собственных значений матрицы T_k, с помощью которых и будет найдены искомые собственные векторы исходной матрицы A.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро на каждой итерации алгоритма Ланцоша состоит в вычислении очередного промежуточного вектора z произведением исходной матрицы A на вектор q_i с предыдущей итерации:
- z = Aq_i
При больших k, сопоставимых с n, к вычислительному ядру можно отнести вычисление собственных значений и собственных векторов трёхдиагональной матрицы. Однако на практике k много меньше n.
1.4 Макроструктура алгоритма
Исходя из предложенной последовательной реализации метода, макрооперациями в алгоритме являются:
- Процедура итеративного построения трехдиагональной симметричной матрицы, включающая:
- умножение матрицы на вектор (состоит из умножения вектора на число и сложения векторов);
- скалярное произведение векторов;
- линейная комбинация векторов (сложение/умножение на вещественные числа);
- вычисление нормы (скалярное произведение векторов и вычисление квадратного корня);
- Вычисление собственных значений и собственных векторов полученной в ходе работы трехдиагональной симметричной матрицы.
При этом, первая макрооперация (построение трехдиагональной матрицы) выполняется строго последовательно. Единственное, что можно распараллелить - это умножение матрицы на вектор. Однако это операция достаточно легковесная, если оперировать, например, разреженной матрицей.
Вычисление собственных значений полученной матрицы на практике выполняется с помощью QR-алгоритма и выходит за рамки описанного алгоритма.
1.5 Схема реализации последовательного алгоритма
Исходные данные: симметричная матрица A, случайный вектор b.
Вычисляемые данные: собственные вектора матрицы T_k являющиеся столбцами матрицы Q_k V, и матрица собственных значений \Lambda, где V, \Lambda из спектрального разложения T_k = V\Lambda V^T.
Алгоритм [4] на псевдокоде:
\begin{align} q_1 = & b/ \|b\|_2,\; \beta_0 = 0,\; q_0 = 0\\ for \; & i = 1 \; to \; k \\ & z = Aq_i\\ & \alpha_i = q^T_i z\\ & z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}\\ & \beta_i = \|z\|_2\\ & If \; \beta_i == 0 \; then \\ & \; \; \; \; exit\\ & else \\ & \; \; \; \; q_{i+1} = z / \beta_i \\ end \; & for \end{align}
После этого вычисляются собственные значения и собственные вектора симметричной трехдиагональной матрицы T_k наиболее удобным образом.
1.6 Последовательная сложность алгоритма
Последовательная сложность алгоритма рассчитана на основе приведенной выше реализации алгоритма. Исходя из псевдокода последовательно выполняются следующие операции:
- Умножение квадратной матрицы n * n на вектор длины n. Требует n * n умножений и сложений;
- Скалярное произведение векторов длины n. Требует n умножений и сложений;
- Сложение векторов длины n. Требует n сложений;
- Умножение вектора длины n на скаляр. Требует n умножений;
- Нахождение квадратичной нормы вектора длины n. Требует n умножений и сложений + извлечения квадратного корня;
- Нахождение собственных значений и векторов трехдиагональной симметричной матрицы размера k \times k . Наиболее эффективный метод метода «Разделяй-и-властвуй» в среднем требует ~O(k^{2.3}) операций.
Суммарное число операций в алгоритме без учета вычисления собственных значений в трехдиагональной памяти:
- kn^2 + n(4k + 1) операций умножения;
- k(n^2+3n-2) + n-1 операций сложения/вычитания;
- n(k + 1) операций деления;
- k + 1 операций вычислений квадратного корня.
Таким образом, в худшем случае, алгоритм Ланцоша имеет сложность O(kn^2) и односится к квадратичным алгоритмам по n при малых k.
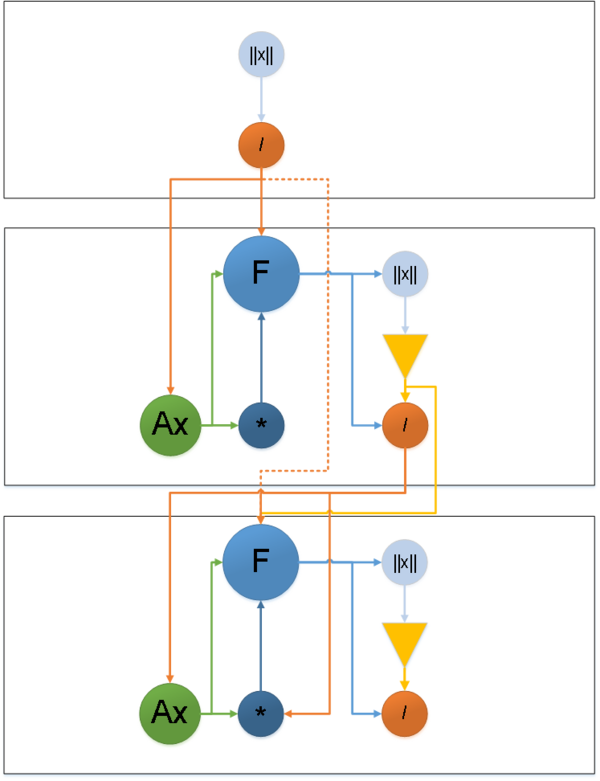
1.7 Информационный граф
Информационный граф алгоритма можно разбить на две части:
- Граф алгоритма с отображением входных и выходных данных.
- Граф линейного оператора.
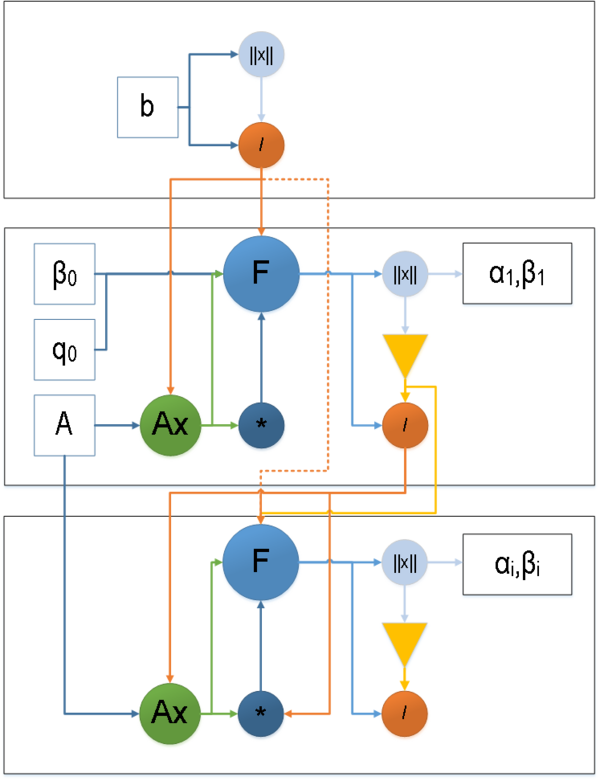
\|x\| — вычисление нормы,
/ — операция деления,
\mathsf{F} — вычисление линейной комбинации векторов,
* — операция умножения,
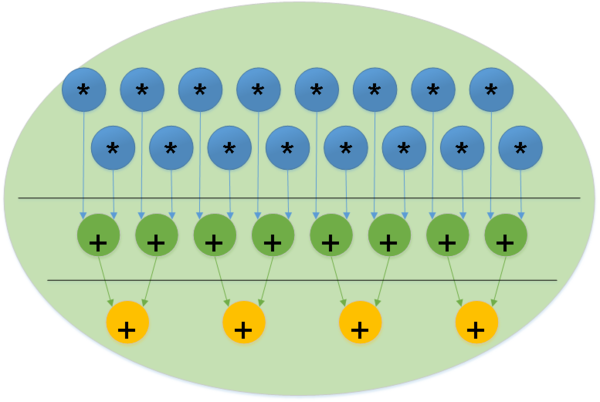
\mathsf{Ax} — линейный оператор (Рисунок 2),
▽ - условие выхода \mathsf{(\beta_i = 0)},
\mathsf{A, b, q_0 = 0, \beta_0 = 0} — входные данные,
\mathsf{\alpha_i, \beta_i} — выходной результат.
Из информационного графа видно, что паралеллизация алгоритма возможна при выполнении линенйного оператора Ax на каждой итерации алгоритма. Затем необходима синхронизация между процессами.
1.8 Ресурс параллелизма алгоритма
Важно заметить, что итерации алгоритма выполняются строго последовательно, а распараллеливание возможно только внутри итераций.
- Умножение A^{n * n} на вектор длины n требует n ярусов умножений и сложенийж
- При этом сложение элементов вектора длины n можно выполнить за \log(n) [2];
- Остальные операции в рамках итерации выполняются последовательно (вычисление значений векторов может быть выполнено за 1 ярус):
- Ресурс параллелизма алгоритма вычисления собственных значений зависит от используемого алгоритма.
Исходя из вышеизложенного, алгоритм Ланцоша обладает O(k\log n)-ой сложностью по высоте ЯПФ и O(n^2)-ой по ширине ЯПФ.
1.9 Входные и выходные данные алгоритма
Входные данные: симметричная вещественная матрица A, случайный вектор b, число итераций k.
Объём входных данных: n(n + 1) + 1 .
Выходные данные: вектор собственных значений \Lambda, матрица собственных векторов E.
Объём выходных данных: k(n + 1).
1.10 Свойства алгоритма
- Сложность последовательного алгоритма O(kn^2);
- По классификации по высоте ЯПФ Алгоритм Ланцоша является алгоритмом со сложностью O(k\log n), при классификации по ширине ЯПФ его сложность O(n^2);
- Таким образом, отношение последовательной сложности к параллельной \frac{kn^2}{k \log{n}};
- Вычислительная мощность алгоритма Ланцоша без переортогонализации из последовательной сложности алгоритма \frac{k(2n^2+8n-1)+3n}{n^2+2k}. При k много меньше n вычислительная мощность ≈ 2k;
- Алгоритм Ланцоша без переортогонализации не является детерминированным из-за того, что возможно выполнение меньшего числа итераций алгоритма, из-за того, что все собственные значения уже вычислены;
- Также алгоритм Ланцоша быстро сходится при вычислении собственных значений матрицы A, находящихся на границе ее спектра (в T_{j} в первую очередь появляются максимальные по модулю собственные значения);
- Из-за использования точной арифметики алгоритм Ланшоца может найти кратные собственные значения, которые на деле оными не являются;
- Нестабильность алгоритма (эффект ложной сходимости) присуще плавающей арифметике, из-за ошибок округления в которой на очередном этапе может быть построен линейно зависимый от исходных новый вектор, что повлечет невозможность дальнейшего приближения собственных значений.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Для исследования масшабируемости алгоритма была написана реализация[3] на языке C++ с использованием MPI. Реализация была протестирована на суперкомпьютере Ломоносов[4].
Были исследованы:
- время выполнения программы в зависимости от размера входных данных (матрицы);
- время выполнения в зависимости от размера параллельных нод.
Дополнительно было измерено время работы исходя из оптимизационных флагов компилятора GCC [5].
Параметры запуска алгоритма:
- размер матрицы от 20000 до 175000 с шагом 2500;
- количество процессоров от 8 до 128 с шагом 8.
Программа запускалась на суперкомьютере "Ломоносов" со следующими характеристиками:
- Компилятор GCC 5.2.1;
- Версия MPI 1.8.4;
- Сборка проводилась командой:
mpic++ -std=c++0x -O2 <CPP_FILE> -lm -static-libstdc++
Полученная эффективность реализации варьируется в пределах от 2% (на маленьких входных данных) до 45% (на больших входных данных и максимальном числе нодов).
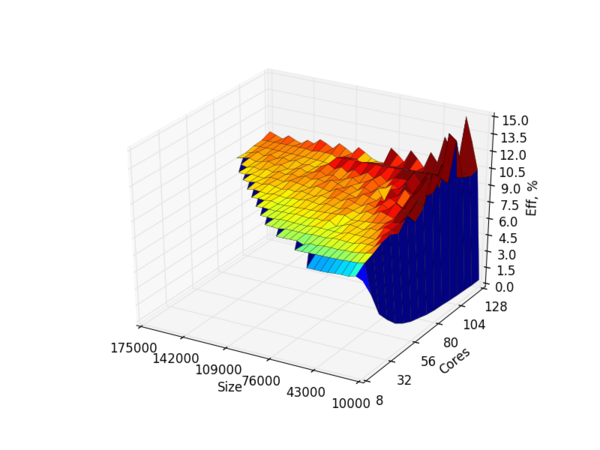
На рисунке 4 представлена эффективность программы при отсутствии флага оптимизации O2.
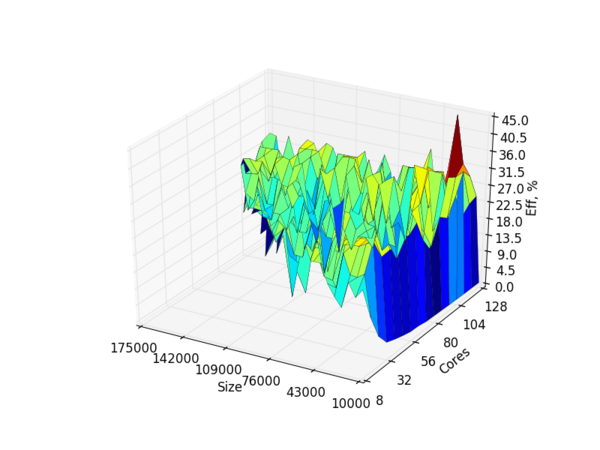
На рисунке 5 представлена эффективность алгоритма с оптимизацией компилятора GCC (-O2).
Как видно из графиков выше, средняя эффективность минимальна при малых входных данных (на размере матрицы в 10000).
В среднем данный показатель держится между 9% и 14%.
При этом, оптимизация компилятора MPIC++ позволяет получить выигрыш в эффективности более чем в 3 раза (45,5% против 14,7%). Однако, как можно заметить из графиков, при оптимизации алгоритм ведет себя более нестабильно, скорее всего из-за значительной траты времени на работу с памятью (более планые участки свидетельствует о том, что необходимые данные нашлись в кеше).
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В настоящее время существует множество реализаций алгоритма Ланцоша итеративного поиска собственных значений, как входящих в официальные дистрибутивы для вычислений (ARPACK), так и неофициальных реализаций, выложенных на Github. Среди них:
1. The IETL Project [5]
2. MatLab [6]
3. ARPACK [7]
4. Julia Math [8]
Также существуют официальные реализации на других языках (например R). Что касается встроенной возможности параллелизма - самыми стабильными в этом плане являются ARPACK, а также IETL.
Для проверки масшабируемости, алгоритм был реализован на языке C++ с применением MPI [6].
3 Литература
- ↑ Lanczos, C. "An iteration method for the solution of the eigenvalue problem of linear differential and integral operators", J. Res. Nat’l Bur. Std. 45, 255-282 (1950).
- ↑ Ojalvo, I.U. and Newman, M., "Vibration modes of large structures by an automatic matrix-reduction method", AIAA J., 8 (7), 1234–1239 (1970).
- ↑ https://ru.wikipedia.org/wiki/Биортогонализация_Ланцоша
- ↑ Деммель Д. Вычислительная линейная алгебра
- ↑ http://www.comp-phys.org/software/ietl/
- ↑ https://www.mathworks.com/matlabcentral/newsreader/view_thread/10554
- ↑ http://www.caam.rice.edu/software/ARPACK/
- ↑ https://github.com/JuliaMath/IterativeSolvers.jl