Уровень алгоритма

Участник:Parkhomenko/Алгоритм k средних

Материал из Алговики
Перейти к навигации Перейти к поиску
Symbol confirmed.svgЭта работа успешно выполнена
Преподавателю: в основное пространство, в подстраницу
Данное задание было проверено и зачтено.
Проверено Konshin и Zhum.



Алгоритм k средних
Последовательный алгоритм
Последовательная сложность [math]O(tnkd)[/math]
Объём входных данных [math]nd[/math]
Объём выходных данных [math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(t \cdot \log nkd)[/math]
Ширина ярусно-параллельной формы [math]O(nkd)[/math]


Основные авторы описания: П.А.Пархоменко (1.1, 1.3, 1.6, 1.8, 1.9, 1.10, 2.4), И.Д.Машонский (1.2, 1.4, 1.5, 1.7, 1.8, 1.10, 2.7)

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм k средних (англ. k-means) - один из алгоритмов машинного обучения, решающий задачу кластеризации. Он был изобретен в середине 1950-х математиком Гуго Штейнгаузом[1] и Стюартом Ллойдом[2]. Алгоритм стал особо популярным после публикации Маккуина[3], в которой впервые был использован термин “k-means”.

Задача алгоритма кластеризации заключается в разбиении N объектов (d-мерных векторов) на K групп (кластеров). Каждый вектор может принадлежать только одному кластеру. Количество кластеров K фиксировано, оно задается в качестве параметра.

K-means является итерационным алгоритмом, разновидностью EM-алгоритма. Основная идея работы алгоритма заключается в проведении некоторого количества итераций, на каждой из которых происходит пересчет центра масс для каждого кластера, полученного на предыдущей итерации. После этого векторы перераспределяются по кластерам: вектор относится к тому кластеру, расстояние до центра масс которого минимально. Алгоритм завершает работу в том случае, если на очередной итерации центры масс кластеров не изменились.

1.2 Математическое описание алгоритма

Исходные данные: множество d-мерных векторов (наблюдений) [math]X[/math] = [math]\{x_1, x_2, ..., x_n\}[/math], число кластеров [math]k \in \mathbb{N}[/math]

В результате работы алгоритма исходное множество векторов [math]X[/math] разбивается на [math]k[/math] непересекающихся множеств (кластеров) [math]S_1, S_2, ..., S_k[/math], таких что [math]X = {\bigcup \limits _{i = 1}^k S_i} [/math] и значение [math]\sum_{i=1}^{k} \sum_{\mathbf x \in S_i} \left\| \mathbf x - \mu_i \right\|^2 [/math] — минимально для всех возможных наборов [math]S_1, S_2, ..., S_k[/math]. Под [math]\mu_i[/math] здесь подразумевается центр масс векторов из множества [math]S_i[/math].

Первоначальные значения центров масс [math]\mu_1^{(1)}, ..., \mu_k^{(1)}[/math] определяются в начале работы алгоритма случайным образом среди векторов множества [math]X[/math].

Алгоритм заключается в попеременном применении двух шагов [4]: распределения векторов по кластерам и обновления центров масс каждого кластера

Распределение векторов по кластерам: на данном шаге каждый вектор распределяется в один из кластеров [math]S_i^{(t)}[/math]:

[math]S_i^{(t)} = \big \{ x_p : \big \| x_p - \mu^{(t)}_i \big \|^2 \le \big \| x_p - \mu^{(t)}_j \big \|^2 \ \forall j, 1 \le j \le k \big\},[/math]

Обновление центров масс: на данном шаге вычисляются новые центры масс для кластеров, полученных на предыдущем шаге.

[math]\mu^{(t+1)}_i = \frac{1}{|S^{(t)}_i|} \sum_{x_j \in S^{(t)}_i} x_j [/math]

Алгоритм завершается, когда на очередном шаге не происходит изменения центров масс кластеров.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательного алгоритма k-means состоит из двух операций, повторяющихся на каждой итерации алгоритма:

  • пересчета центров масс кластеров;
  • соотнесения каждого вектора к одному из кластеров.

Пересчет центра масс кластера заключается в нахождении d-мерного вектора, являющегося средним арифметическим d-мерных векторов, принадлежащих кластеру. Эту операцию необходимо выполнять для каждого из K кластеров.

Для соотнесения вектора к одному из кластеров, необходимо для каждого из N вектора посчитать расстояние до центров масс всех K кластеров. Для нахождения расстояния между двумя d-мерными векторами p и q используется Евклидова метрика: [math]\sqrt{\sum_{k=1}^d (p_k-q_k)^2}[/math]

1.4 Макроструктура алгоритма

Инициализация центров масс кластеров

В начале алгоритма осуществляется инициализация центров масс [math]\mu_1^{(1)}, ..., \mu_k^{(1)}[/math], которая может быть реализована двумя возможными способами [5]:

  • случайный выбор центров масс среди исходных наблюдений [math]x_1, x_2, ..., x_n[/math];
  • все наблюдения случайным образом распределяются по кластерам [math]S_1, S_2, ..., S_k[/math], а затем для каждого кластера выполняется операция обновления центра масс.

Распределение векторов по кластерам

На шаге распределения векторов по кластерам производится операция нахождения квадратов расстояний между векторами кластера и центром масс кластера:

[math]\rho = \big \| x_p - \mu^{(t)}_i \big \|^2[/math]

Обновление центров масс кластеров

На шаге обновления центров масс производится операция суммирования векторов кластера:

[math]\mu^{(t+1)}_i = \frac{1}{|S^{(t)}_i|} \sum_{x_j \in S^{(t)}_i} x_j [/math]

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

  1. Инициализируются центры масс [math]\mu_1^{(1)}, ..., \mu_k^{(1)}[/math]
  2. [math]t := 1[/math]
  3. Для каждого вектора [math]x_i, i = 1, 2, ..., n[/math] вычисляется
    [math]m = \underset{j \in \{1, 2, ..., k\}} {\operatorname{arg\,min}} \big \| x_i - \mu^{(t)}_j \big \|^2[/math],
    вектор [math]x_i[/math] распределяется в кластер [math]S^{(t)}_m[/math]
  4. Для каждого [math]j = 1, 2, ..., k[/math] вычисляется
    [math]\mu^{(t+1)}_j = \frac{1}{|S^{(t)}_i|} \sum_{x_j \in S^{(t)}_i} x_j [/math]
  5. Если [math]\mu^{(t)}_j = \mu^{(t+1)}_j, j = 1, 2, ..., k[/math], завершить выполнение алгоритма, иначе [math]t := t + 1[/math], переход на шаг 3.

1.6 Последовательная сложность алгоритма

Для вычисления центра массы кластера, содержащего [math]n_i[/math] d-мерных векторов, необходимо:

  • [math]n_i \cdot (d - 1)[/math] операций сложения
  • [math]d[/math] операций деления

Для определения центров масс всех k кластеров требуется:

  • [math]n \cdot (d - 1)[/math] операций сложения
  • [math]k \cdot d[/math] операций деления

Для определения расстояния между двумя d-мерными векторами, требуется:

  • [math]d[/math] операций вычитания
  • [math]d[/math] операций умножения
  • [math]d - 1[/math] операций сложения

Для определения кластера для n d-мерного векторов, необходимо:

  • [math]n \cdot k \cdot d[/math] операций вычитания
  • [math]n \cdot k \cdot d[/math] операций умножения
  • [math]n \cdot k \cdot (d - 1)[/math] операций сложения

Таким образом, общая сложность одной итерации:

  • [math]O(n k d)[/math] операций сложения/вычитания
  • [math]O(n k d)[/math] операций умножения/деления

Сложность всего алгоритма, состоящего из [math]t[/math] итераций: [math]O(t n k d)[/math]

1.7 Информационный граф

В данном разделе описывается информационный граф алгоритма k-средних при [math]n = 3, k = 2[/math]

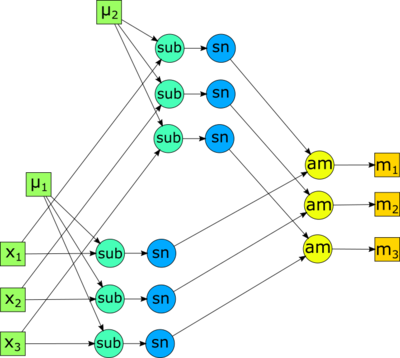
На рисунке 1 показана общая структура алгоритма: в качестве входных данных выступает матрица, строками которой являются входные векторы [math]x_1, x_2, x_3[/math], на выходе получается массив из [math]n[/math] чисел, где элемент с номером [math]i = 1, 2, 3[/math] обозначает номер кластера, которому принадлежит вектор [math]x_i[/math]. На шаге [math]init[/math] происходит инициализация значений центров масс кластеров, после этого осуществляется итеративное повторение этапов распределения векторов по кластерам ([math]as[/math]) и обновления значений центров масс кластеров ([math]up[/math]). Когда на очередном шаге обновления центров масс кластеров значения центров масс не изменяются, алгоритм завершает работу, и в качестве выходных данных выступают номера кластеров для каждого из входных векторов.

Рисунок 1. Общая схема работы алгоритма k-средних

Распределение векторов по кластерам. На рисунке 2 изображен информационный граф для этапа распределения векторов по кластерам. В качестве входных данных выступают строки входной матрицы (входные векторы) [math]x_1, x_2, x_3[/math] и текущие значения центров масс кластеров [math]\mu_1, \mu_2[/math] (вычисленные на этапе инициализации или предшествующего этапа обновления центров масс кластеров). В качестве выходных данных выступают числа [math]m_1, m_2, m_3[/math], где [math]m_i, i = 1, 2, 3[/math] - номер кластера, содержащего вектор [math]x_i[/math]. Вершинами с пометкой [math]sub[/math] обозначены операции векторной разности, вершинами [math]sn[/math] - операция вычисления квадрата нормы вектора, вершинами [math]am[/math] - операция [math]\underset{i \in \{1, 2\}} {\operatorname{arg\,min}} p_i[/math].

Рисунок 2. Граф алгоритма для этапа распределения векторов по кластерам

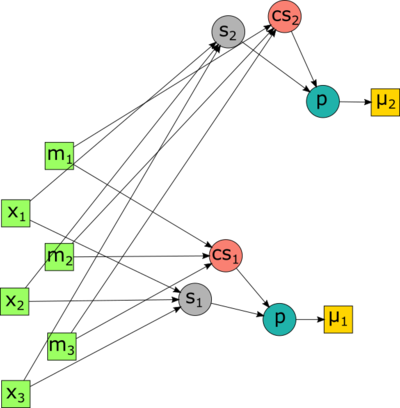
Обновление центров масс кластеров. На рисунке 3 представлен информационный граф для этапа обновления центров масс кластеров. В качестве входных данных выступают строки входной матрицы (входные векторы) [math]x_1, x_2, x_3[/math] с соответствующими номерами кластеров [math]m_1, m_2, m_3[/math], содержащих эти векторы. В качестве выходных данных здесь выступают обновленные значения центров масс кластеров: [math]\mu_1, \mu_2[/math]. Вершинами с пометками [math]s_i, i = 1, 2[/math] обозначены операции суммирования векторов, принадлежащих кластеру [math]i[/math]. Вершинами с пометками [math]cs_i, i = 1, 2[/math] обозначены операции вычисления выражения [math]1 / |S_i|[/math], где за [math]S_i[/math] обозначен кластер с номером [math]i[/math]. Вершинами с пометкой [math]p[/math] обозначена операция произведения.

Рисунок 3. Граф алгоритма для этапа обновления центров масс кластеров

1.8 Ресурс параллелизма алгоритма

Алгоритм кластеризации k средних имеет место массовый параллелизм: в основе каждого из основных этапов алгоритма (распределения векторов по кластерам и обновления центров масс кластеров) лежат циклы, итерации которых являются информационно независимыми. Учитывая данный факт можно оценить параллельную сложность алгоритма в предположении доступности неограниченного числа необходимых процессоров.

В силу особенностей алгоритма k средних порядок выполнения основных этапов существенен, что не позволяет выполнять их параллельно. Таким образом, итоговая сложность параллельного алгоритма будет определяться, исходя из формулы [math]T = t \cdot (T_{as} + T_{up})[/math], где [math]T_{as}[/math] - параллельная сложность этапа распределения векторов по кластерам, [math]T_{up}[/math] - параллельная сложность этапа обновления центров масс кластеров, [math]t[/math] - общее число итераций алгоритма.

Параллельная сложность этапа распределения векторов по кластерам с учетом доступности неограниченного числа процессоров вычисляется следующим образом: так как вычисление значений [math]\big \| x_i - \mu^{(t)}_j \big \|^2[/math] для каждой пары векторов [math]x_i, i = 1, 2, ..., n[/math] и [math]\mu^{(t)}_j, j = 1, 2, ..., k[/math] можно выполнять независимо и для вычисления этого выражения требуется [math]O(\log d)[/math] операций в соответствии с параллельной реализацией нахождения сумм элементов массива сдваиванием. Параллельная сложность реализации операции нахождения минимума из [math]k[/math] элементов определяется как [math]O(\log k)[/math]. Таким образом, сложность этапа распределения векторов по кластерам [math]O(\log kd)[/math].

Параллельная сложность этапа обновления центров масс кластеров вычисляется следующим образом: так как обновление значений каждого из центров масс кластеров можно выполнять независимо, параллельная сложность определяется сложностью обновления центра масс самого большого кластера. В худшем случае для нахождения значения выражения [math]\mu^{(t+1)}_j = \frac{1}{|S^{(t)}_i|} \sum_{x_j \in S^{(t)}_i} x_j [/math] требуется [math]O(\log n)[/math] операций.

С учетом вышесказанного, итоговая параллельная сложность алгоритма k средних определяется выражением [math]O(t \cdot \log nkd)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные:

  • целое неотрицательное число [math]k[/math] - количество кластеров;
  • матрица координат векторов [math]A[/math] размерностью [math]n * d[/math].

Объем входных данных:

  • [math]n * d[/math] вещественных чисел (если координаты вещественные числа), [math]1[/math] целое неотрицательное число.

Выходные данные:

  • вектор длины [math]n[/math] - для каждого вектора указан номер кластера.

Объем выходных данных:

  • [math]n[/math] целых неотрицательных чисел.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности алгоритма равно [math]\frac{O(tnkd)}{O(t \cdot \log nkd)}[/math].

Число операций алгоритма k средних оценивается как [math]O(tnkd)[/math], суммарный объем входных и выходных данных равен [math]n(d+1)[/math]. Следовательно, вычислительная мощность алгоритма линейна по [math]k[/math] и линейна по [math]t[/math].

Стоит отметить следующие ключевые особенности алгоритма k средних:

  • Алгоритм прост в реализации и имеет высокую скорость работы по сравнению с другими алгоритмами кластеризации (при удачном выборе начальных значений центров масс кластеров)
  • В качестве метрики используется евклидово расстояние, а в качестве меры разброса кластера используется дисперсия
  • Количество кластеров k является входным параметром алгоритма, поэтому неправильный выбор этого параметра может негативно повлиять на качество кластеризации
  • Сходимость алгоритма к локальному минимуму может породить некорректный конечный результат работы
  • Алгоритм очень чувствителен к выбору начальных центров масс кластеров: классический вариант подразумевает случайный их выбор, что может являться источником погрешности. Из этого и предыдущего свойства следует то, что алгоритм не является устойчивым.

Как и любой другой алгоритм кластеризации, результат работы алгоритма k средних зависит от того, удовлетворяет ли входной набор данных предположениям, на которые опираются алгоритмы кластеризации. Таким образом, на одних наборах данных алгоритм может показывать хорошие результаты, но на других выдавать некорректные результаты.

Алгоритм не является детерминированным, в силу того, что он чувствителен к выбору начальных центров масс кластеров, который осуществляется, как правило, случайным образом и тем самым вносит различия в работу алгоритма от запуска к запуску.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости алгоритма k-means в зависимости от количества используемых процессов было проведено в статье Кумара[6]. Исследование происходило на суперкомпьютере Jaguar - Cray XT5[7]. На момент экспериментов данный суперкомпьютер имел следующую конфигурацию: 18,688 вычислительных узлов с двумя шестнадцатиядерными процессорами AMD Opteron 2435 (Istanbul) 2.6 GHz, 16 GB of DDR2-800 оперативной памяти, и SeaStar 2+ роутер. Всего он состоял из 224,256 вычислительных ядер, 300 TB памяти, и пиковой производительностью 2.3 petaflops.

Реализация алгоритма была выполнена на языке программирования C с использованием MPI.

Объем данных составлял 84 гигабайта, количество объектов (d-мерных векторов) n равнялось 1,024,767,667, размерность векторов d равнялась 22, количество кластеров k равнялось 1000.

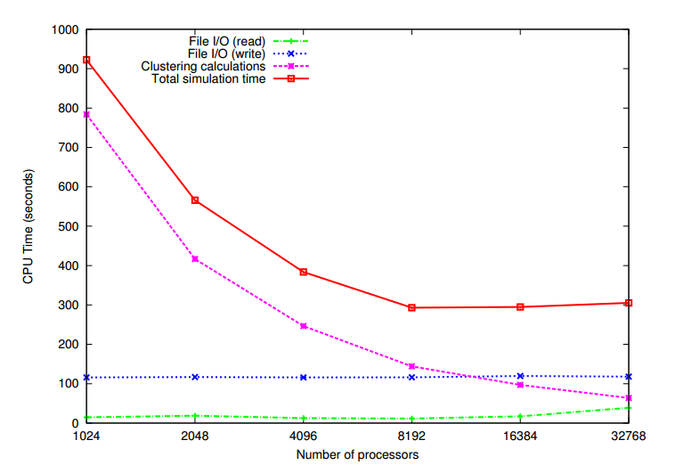
На рисунке 4 показана зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров. Можно отметить, что время, затраченное на чтение данных и запись результатов кластеризации, практически не изменяется с увеличением количества задействованных процессоров. Время же работы самого алгоритма кластеризации уменьшается с увеличением количества процессоров.

Рисунок 4. Зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров.

Также было произведено самостоятельное исследование масштабируемости алгоритма. Исследование производилось на суперкомпьютере "Blue Gene/P"[8].

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

  • число процессоров [1, 2, 4, 8, 16, 32, 64, 128, 256, 512];
  • количество объектов [5000, 10000, 25000, 50000].

Был использован набор данных Dataset for Sensorless Drive Diagnosis Data Set[9] из репозитория Machine learning repository[10].

Исследуемый набор данных содержит векторы, размерность которых равна 49. Компоненты векторов являются вещественными числами. Количество кластеров равно 11. Пропущенные значения отсутствуют.

Для исследования масштабируемости алгоритма была использована реализация на языке C с использованием MPI[11]. Код можно найти здесь: https://github.com/serban/kmeans. Данная реализация предоставляет возможность распараллеливать решение задачи с помощью технологий MPI, OpenMP И CUDA. Для запуска MPI-версии программы использовалась цель "mpi_main" Makefile.

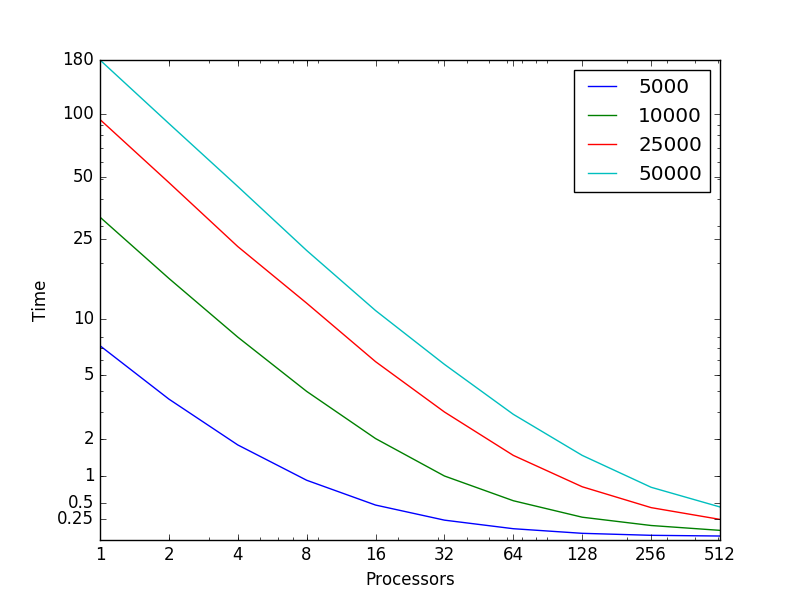
На рисунке 5 показана зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров (использовались логарифмические оси). Разными цветами помечены запуски, соответствующие разным количествам объектам, участвующих в кластеризации. Можно видеть близкое к линейному увеличение времени работы программы в зависимости от количества процессоров. Также можно видеть увеличение времени работы алгоритма при увеличении количества объектов.

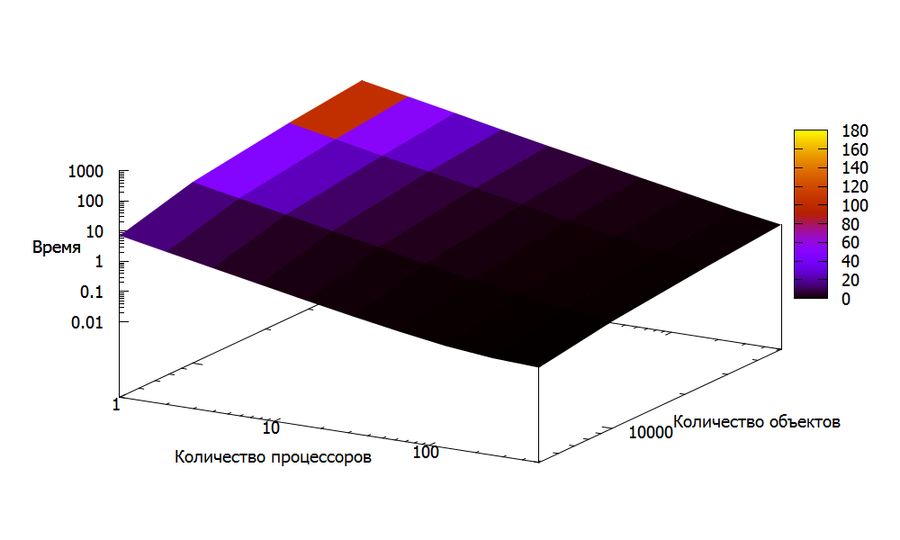
Рисунок 5. Зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров.

На рисунке 6 показана эта же зависимость, только в трехмерном пространстве. Аналогично с рисунком 5, были использованы логарифмические оси. Как и в случае двумерного рисунка, можно видеть близкое к линейному увеличение времени работы программы.

Рисунок 6. Зависимости времени работы алгоритма кластеризации k-means в зависимости от количества используемых процессоров.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Существуют следующие реализации алгоритма k-средних:

  • scikit-learn библиотека машинного обучения для языка Python.
  • SciPy библиотека на языке Python, содержащая большое число реализаций различных алгоритмов, в том числе k-средних.
  • ELKI библиотека для анализа данных на языке программирования Java, содержит различные алгоритмы кластеризации, в том числе k-средних.
  • MLPACK библиотека машинного обучения для C++, содержит реализацию алгоритма k-средних.
  • Julia k-means реализация алгоритма k-средних на языке программирования Julia.
  • OpenCV библиотека содержит реализацию k-средних.
  • Apache Mahout содержит реализацию алгоритма k-средних на базе MapReduce.
  • Weka библиотека и инструмент для анализа данных на языке Java.
  • Torch библиотека машинного обучения на базе языка программирования Lua.
  • Apache Spark MLlib содержит распределенную реализацию алгоритма k-средних.
  • Accord.NET содержит несколько различных реализаций k-средних на языке C#.
  • R k-means реализация k-средних на языке R.

3 Литература

<references \>

  1. ↑ Steinhaus H. (1956). Sur la division des corps materiels en parties. Bull. Acad. Polon. Sci., C1. III vol IV: 801—804.
  2. ↑ Lloyd S. (1957). Least square quantization in PCM’s. Bell Telephone Laboratories Paper.
  3. ↑ MacQueen J. (1967). Some methods for classification and analysis of multivariate observations. In Proc. 5th Berkeley Symp. on Math. Statistics and Probability, pages 281—297.
  4. ↑ MacKay, David (2003). "Chapter 20. An Example Inference Task: Clustering" (PDF). Information Theory, Inference and Learning Algorithms. Cambridge University Press. pp. 284–292.
  5. ↑ Hamerly, G.; Elkan, C. (2002). "Alternatives to the k-means algorithm that find better clusterings" (PDF). Proceedings of the eleventh international conference on Information and knowledge management (CIKM).
  6. ↑ Kumar, J., Mills, R. T., Hoffman, F. M., & Hargrove, W. W. (2011). Parallel k-means clustering for quantitative ecoregion delineation using large data sets. Procedia Computer Science, 4, 1602-1611.
  7. ↑ https://www.top500.org/system/176029
  8. ↑ http://hpc.cmc.msu.ru/bgp
  9. ↑ PASCHKE, Fabian ; BAYER, Christian ; BATOR, Martyna ; MÖNKS, Uwe ; DICKS, Alexander ; ENGE-ROSENBLATT, Olaf ; LOHWEG, Volker: Sensorlose Zustandsüberwachung an Synchronmotoren, Bd. 46. In: HOFFMANN, Frank; HÃœLLERMEIER, Eyke (Hrsg.): Proceedings 23. Workshop Computational Intelligence. Karlsruhe : KIT Scientific Publishing, 2013 (Schriftenreihe des Instituts für Angewandte Informatik - Automatisierungstechnik am Karlsruher Institut für Technologie, 46), S. 211-225
  10. ↑ https://archive.ics.uci.edu/ml/datasets/Dataset+for+Sensorless+Drive+Diagnosis
  11. ↑ http://users.eecs.northwestern.edu/~wkliao/Kmeans/index.html
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Parkhomenko/Алгоритм_k_средних&oldid=21379