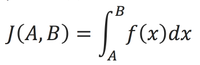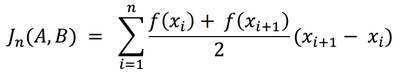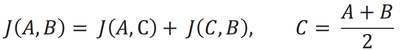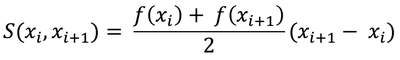Участник:Joinmek/Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки: различия между версиями
Joinmek (обсуждение | вклад) (Новая страница: «Основные авторы описания: Можарова В. А. == Общее описание алгоритма == Основная идея бол…») |
Joinmek (обсуждение | вклад) |
||
| Строка 6: | Строка 6: | ||
Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). | Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона). | ||
| − | [[Файл:vm_trap. | + | [[Файл:vm_trap.png|300px|center]] |
Чтобы посчитать определенный интеграл, участок интегрирования делится на отрезки, на которых подсчитывается значение новой (упрощенной) функции, после чего значения суммируются на всех отрезках. Но чтобы посчитать интеграл с определенной точностью, мы не можем заранее узнать, какие размеры отрезков, нужно использовать, т. к. это зависит от самой функции. Для этого используют адаптивное разбиение участка интегрирования: размер конкретного отрезка определяется во время подсчета значения функции на нем самом. Если заданная точность не была достигнута на данном отрезке, он рекурсивно разбивается на несколько новых и функция подсчитывается уже на них. Таким образом, выигрыш от применения рассмотренного алгоритма рекурсивного разбиения достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования. | Чтобы посчитать определенный интеграл, участок интегрирования делится на отрезки, на которых подсчитывается значение новой (упрощенной) функции, после чего значения суммируются на всех отрезках. Но чтобы посчитать интеграл с определенной точностью, мы не можем заранее узнать, какие размеры отрезков, нужно использовать, т. к. это зависит от самой функции. Для этого используют адаптивное разбиение участка интегрирования: размер конкретного отрезка определяется во время подсчета значения функции на нем самом. Если заданная точность не была достигнута на данном отрезке, он рекурсивно разбивается на несколько новых и функция подсчитывается уже на них. Таким образом, выигрыш от применения рассмотренного алгоритма рекурсивного разбиения достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования. | ||
| Строка 14: | Строка 14: | ||
Пусть у нас есть интеграл, который надо вычислить с точностью ε: | Пусть у нас есть интеграл, который надо вычислить с точностью ε: | ||
| + | [[Файл:vm_integral.png|200px|center]] | ||
Предположим, что в результате адаптации сетки для данной функции, на отрезке [A, B] получилась сетка, содержащая n + 1 узел. Тогда согласно методу трапеций, можно численно найти определенный интеграл от функции f(x) на отрезке [A, B]: | Предположим, что в результате адаптации сетки для данной функции, на отрезке [A, B] получилась сетка, содержащая n + 1 узел. Тогда согласно методу трапеций, можно численно найти определенный интеграл от функции f(x) на отрезке [A, B]: | ||
| − | [[Файл:vm_common. | + | |
| + | [[Файл:vm_common.png|400px|center]] | ||
| + | |||
Будем полагать значение J найденным с точностью ε, если выполнено условие: | Будем полагать значение J найденным с точностью ε, если выполнено условие: | ||
| + | |||
| + | [[Файл:vm_condition.png|300px|center]] | ||
где n<sub>1</sub> и n<sub>2</sub> - количество узлов, образующих две разные сетки. | где n<sub>1</sub> и n<sub>2</sub> - количество узлов, образующих две разные сетки. | ||
Пользуясь формулой | Пользуясь формулой | ||
| + | |||
| + | [[Файл:vm_div.png|400px|center]] | ||
рекурсивно делим отрезки интегрирования до достижения на них заданной точности. | рекурсивно делим отрезки интегрирования до достижения на них заданной точности. | ||
| Строка 26: | Строка 33: | ||
== Вычислительное ядро алгоритма == | == Вычислительное ядро алгоритма == | ||
Основное время работы алгоритма приходится на вычисление площадей на отрезках, получившихся в результате рекурсивного разбиения: | Основное время работы алгоритма приходится на вычисление площадей на отрезках, получившихся в результате рекурсивного разбиения: | ||
| + | |||
| + | [[Файл:vm_sq.png|400px|center]] | ||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| Строка 37: | Строка 46: | ||
У стека определен следующий набор операций: | У стека определен следующий набор операций: | ||
| − | + | ||
| + | 1. PUT_INTO_STACK - положить элемент в стек | ||
#define PUT_INTO_STACK(A, B, fA, fB, s) | #define PUT_INTO_STACK(A, B, fA, fB, s) | ||
| Строка 49: | Строка 59: | ||
} | } | ||
| − | + | 2. GET_FROM_STACK - взять верхний элемент из стека | |
#define GET_FROM_STACK(A, B, fA, fB, s) | #define GET_FROM_STACK(A, B, fA, fB, s) | ||
{ | { | ||
| Строка 60: | Строка 70: | ||
} | } | ||
| − | + | 3. STACK_IS_NOT_FREE - проверить стек на наличие в нем элементов | |
| − | |||
#define STACK_IS_NOT_FREE (sp > 0) | #define STACK_IS_NOT_FREE (sp > 0) | ||
== Схема реализации алгоритма == | == Схема реализации алгоритма == | ||
| − | LocalStack (A, B) | + | LocalStack (A, B) |
{ | { | ||
J=0 | J=0 | ||
| Строка 80: | Строка 89: | ||
sACB = sAC + sCB | sACB = sAC + sCB | ||
if (|sAB - sACB| ≥ ε|sACB|) { | if (|sAB - sACB| ≥ ε|sACB|) { | ||
| − | PUT_INTO_STACK( A, C, fA, fC, sAC) | + | PUT_INTO_STACK(A, C, fA, fC, sAC) |
A = C | A = C | ||
fA = fC | fA = fC | ||
| Строка 89: | Строка 98: | ||
if (STACK_IS_NOT_FREE) | if (STACK_IS_NOT_FREE) | ||
break | break | ||
| − | GET_FROM_STACK( A, B, fA, fB, sAB) | + | GET_FROM_STACK(A, B, fA, fB, sAB) |
} | } | ||
} | } | ||
| Строка 98: | Строка 107: | ||
== Информационный граф == | == Информационный граф == | ||
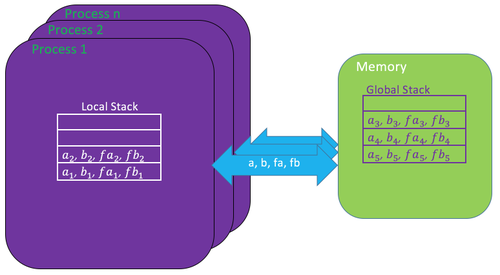
В параллельной версии алгоритма, появляется дополнительный глобальный стек, доступ к которому имеют все процессы. Он находится в общей памяти и так же содержит границы отрезков. Процессы обмениваются с ним данными, распределяя таким образом отрезки между собой. Когда в локальном стеке заканчиваются элементы, процесс обращается к глобальному стеку, чтобы получить их. Причем любой процесс может отдавать ему отрезки, если глобальный стек пуст в то время, как локальный имеет более одного отрезка. | В параллельной версии алгоритма, появляется дополнительный глобальный стек, доступ к которому имеют все процессы. Он находится в общей памяти и так же содержит границы отрезков. Процессы обмениваются с ним данными, распределяя таким образом отрезки между собой. Когда в локальном стеке заканчиваются элементы, процесс обращается к глобальному стеку, чтобы получить их. Причем любой процесс может отдавать ему отрезки, если глобальный стек пуст в то время, как локальный имеет более одного отрезка. | ||
| + | |||
| + | [[Файл:vm_infograph.png|500px|center]] | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| Строка 104: | Строка 115: | ||
На выходе: число – значение определенного интеграла. | На выходе: число – значение определенного интеграла. | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| − | + | ||
| − | + | 1. Алгоритм адаптируется под сложность функции | |
| − | + | ||
| − | + | 2. Для каждого узла сетки значение функции высчитывается один раз | |
| − | + | ||
| + | 3. В параллельной версии алгоритма не требуется управляющий процесс | ||
| + | |||
| + | 4. Алгоритм является детерминированным | ||
| + | |||
| + | 5. Степень исхода вершины информационного графа равна 1, т. к. результат работы каждого процесса в дальнейшем используется только 1 раз. | ||
| + | |||
| + | 6. В представленном параллельном алгоритме сбалансирована загрузка процессов, т. к. при завершении своих задач каждый процессор обращается за новыми в глобальный стек | ||
| + | |||
| + | 7. Данный алгоритм является устойчивым | ||
Версия 22:09, 15 октября 2016
Основные авторы описания: Можарова В. А.
Содержание
- 1 Общее описание алгоритма
- 2 Математическое описание алгоритма
- 3 Вычислительное ядро алгоритма
- 4 Макроструктура алгоритма
- 5 Схема реализации алгоритма
- 6 Последовательная сложность алгоритма
- 7 Информационный граф
- 8 Ресурс параллелизма алгоритма
- 9 Входные и выходные данные алгоритма
- 10 Свойства алгоритма
1 Общее описание алгоритма
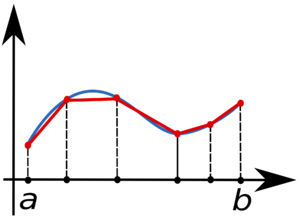
Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона).
Чтобы посчитать определенный интеграл, участок интегрирования делится на отрезки, на которых подсчитывается значение новой (упрощенной) функции, после чего значения суммируются на всех отрезках. Но чтобы посчитать интеграл с определенной точностью, мы не можем заранее узнать, какие размеры отрезков, нужно использовать, т. к. это зависит от самой функции. Для этого используют адаптивное разбиение участка интегрирования: размер конкретного отрезка определяется во время подсчета значения функции на нем самом. Если заданная точность не была достигнута на данном отрезке, он рекурсивно разбивается на несколько новых и функция подсчитывается уже на них. Таким образом, выигрыш от применения рассмотренного алгоритма рекурсивного разбиения достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования.
2 Математическое описание алгоритма
Пусть у нас есть интеграл, который надо вычислить с точностью ε:
Предположим, что в результате адаптации сетки для данной функции, на отрезке [A, B] получилась сетка, содержащая n + 1 узел. Тогда согласно методу трапеций, можно численно найти определенный интеграл от функции f(x) на отрезке [A, B]:
Будем полагать значение J найденным с точностью ε, если выполнено условие:
где n1 и n2 - количество узлов, образующих две разные сетки. Пользуясь формулой
рекурсивно делим отрезки интегрирования до достижения на них заданной точности.
3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на вычисление площадей на отрезках, получившихся в результате рекурсивного разбиения:
4 Макроструктура алгоритма
Для хранения отрезков интегрирования в данном алгоритме понадобится стек.
sp=0 // указатель вершины стека
struct {
A, B, fA, fB, s
} stk[1000]
У стека определен следующий набор операций:
1. PUT_INTO_STACK - положить элемент в стек
#define PUT_INTO_STACK(A, B, fA, fB, s)
{
stk[sp].A=A
stk[sp].B=B
stk[sp].fA=fA
stk[sp].fB=fB
stk[sp].s=s
sp++
}
2. GET_FROM_STACK - взять верхний элемент из стека
#define GET_FROM_STACK(A, B, fA, fB, s)
{
sp--
A=stk[sp].A
B=stk[sp].B
fA=stk[sp].fA
fB=stk[sp].fB
s=stk[sp].s
}
3. STACK_IS_NOT_FREE - проверить стек на наличие в нем элементов
#define STACK_IS_NOT_FREE (sp > 0)
5 Схема реализации алгоритма
LocalStack (A, B)
{
J=0
fA = f(A)
fB = f(B)
sAB = (fA + fB) * (B - A) / 2
while (1)
{
C = (A + B) / 2
fc = fun(C)
sAC = (fA + fC) * (C - A) / 2
sCB = (fC + fB ) * (B-C)/2
sACB = sAC + sCB
if (|sAB - sACB| ≥ ε|sACB|) {
PUT_INTO_STACK(A, C, fA, fC, sAC)
A = C
fA = fC
sAB = sCB
} else
{
J += sACB
if (STACK_IS_NOT_FREE)
break
GET_FROM_STACK(A, B, fA, fB, sAB)
}
}
return J
}
6 Последовательная сложность алгоритма
7 Информационный граф
В параллельной версии алгоритма, появляется дополнительный глобальный стек, доступ к которому имеют все процессы. Он находится в общей памяти и так же содержит границы отрезков. Процессы обмениваются с ним данными, распределяя таким образом отрезки между собой. Когда в локальном стеке заканчиваются элементы, процесс обращается к глобальному стеку, чтобы получить их. Причем любой процесс может отдавать ему отрезки, если глобальный стек пуст в то время, как локальный имеет более одного отрезка.
8 Ресурс параллелизма алгоритма
9 Входные и выходные данные алгоритма
На вход алгоритму подается подынтегральная функция, пределы интегрирования и значение точности, с которой нужно посчитать заданный интеграл. На выходе: число – значение определенного интеграла.
10 Свойства алгоритма
1. Алгоритм адаптируется под сложность функции
2. Для каждого узла сетки значение функции высчитывается один раз
3. В параллельной версии алгоритма не требуется управляющий процесс
4. Алгоритм является детерминированным
5. Степень исхода вершины информационного графа равна 1, т. к. результат работы каждого процесса в дальнейшем используется только 1 раз.
6. В представленном параллельном алгоритме сбалансирована загрузка процессов, т. к. при завершении своих задач каждый процессор обращается за новыми в глобальный стек
7. Данный алгоритм является устойчивым