Участник:Маркова Екатерина/Построение матрицы Адамара: различия между версиями
Katemeron (обсуждение | вклад) |
Katemeron (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{algorithm | {{algorithm | ||
| name = Построение матрицы Адамара | | name = Построение матрицы Адамара | ||
| − | | serial_complexity = <math>O( | + | | serial_complexity = <math>O(N^2)</math> |
| pf_height = <math></math> | | pf_height = <math></math> | ||
| pf_width = <math></math> | | pf_width = <math></math> | ||
| input_data = <math>1</math> | | input_data = <math>1</math> | ||
| − | | output_data = <math> | + | | output_data = <math>N^2</math> |
}} | }} | ||
Основной автор статьи: Маркова Е.А. 615 гр. | Основной автор статьи: Маркова Е.А. 615 гр. | ||
Версия 16:53, 28 октября 2016
| Построение матрицы Адамара | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(N^2)[/math] |
| Объём входных данных | [math]1[/math] |
| Объём выходных данных | [math]N^2[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math][/math] |
| Ширина ярусно-параллельной формы | [math][/math] |
Основной автор статьи: Маркова Е.А. 615 гр.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Матрица Адамара [math]H[/math] - это квадратная матрица размера [math]N\times N[/math], составленная из чисел [math]1[/math] и [math]-1[/math], столбцы которой ортогональны, так что справедливо соотношение:
[math]H*H^T = N*E_N[/math],
где [math]E_N[/math] - это единичная матрица размера [math]N[/math]. Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов.
1.2 Математическое описание алгоритма
Пусть [math]H_m[/math] [math]-[/math] матрица Адамара порядка [math]2^m[/math] и [math]-H_m[/math] [math]-[/math] матрица с противоположными элементами. Тогда матрица [math]H_{2m}[/math] получается следующим образом: [math]H_{2m} = \begin{bmatrix} H_m & H_m \\ H_m & -H_m \end{bmatrix} [/math]
Данным алгоритм описывает получение матриц Адамара только порядка степени 2, то есть [math]m[/math] и [math]N[/math] связаны соотношением [math]N = 2^m[/math].
Получение матрицы порядка [math]N[/math] состоит из следующих [math]m[/math] шагов:
Шаг 1: [math]H_1 = (1);[/math]
Шаг 2: [math]H_2 = \begin{pmatrix} 1 & 1 \\1 & -1 \end{pmatrix}; [/math]
Шаг 3: [math]H_3 = \begin{pmatrix} 1 & 1 & 1 & 1 \\1 & -1 & 1 & -1 \\1 & 1 &- 1 & -1 \\1 & -1 & -1 & 1 \end{pmatrix}. [/math]
...
Шаг [math]m[/math]: искомая матрица [math]H_m[/math].
1.3 Вычислительное ядро алгоритма
Вычислительное ядро рекурсивного алгоритма состоит из [math]\;N^2\;[/math] присвоений значений матрицы Адамара
[math]H_{1,1} = 1[/math];
[math]H_{ij} = H_{i(j - \frac{N}{2})}[/math], где [math]i = 1..\frac{N}{2}[/math], [math]j = \frac{N}{2}+1..N[/math];
[math]H_{ij} = H_{(i-\frac{N}{2})j}[/math], где [math]i = \frac{N}{2}+1..N[/math], [math]j = 1.. \frac{N}{2}[/math];
[math]H_{ij} = H_{(i-\frac{N}{2})(j-\frac{N}{2})}[/math], где [math]i = \frac{N}{2}+1..N [/math], [math]j = \frac{N}{2}+1..N[/math].
1.4 Макроструктура алгоритма
Алгоритм не использует в качестве составных частей другие алгоритмы. Как это было описано в вычислительном ядре, в пустые блоки дублируются со сменой или без смены знака значения первого блока матрицы.
1.5 Схема реализации последовательного алгоритма
В описанном виде алгоритм представляет из себя примитивное дублирование элементов матрицы, полученной на предыдущем этапе, в пустующие блоки новой матрицы.
Сначала заполняется правый верхний блок матрицы [math]H[/math]
[math]H_{ij} = H_{i(j - \frac{N}{2})}[/math], где [math]i = 1..\frac{N}{2}[/math], [math]j = \frac{N}{2}+1..N[/math];
затем левый нижний блок
[math]H_{ij} = H_{(i-\frac{N}{2})j}[/math], где [math]i = \frac{N}{2}+1..N[/math], [math]j = 1.. \frac{N}{2}[/math].
Последним заполняется нижний правый блок матрицы
[math]H_{ij} = H_{(i-\frac{N}{2})(j-\frac{N}{2})}[/math], где [math]i = \frac{N}{2}+1..N [/math], [math]j = \frac{N}{2}+1..N[/math].
1.6 Последовательная сложность алгоритма
Для заполнения матрицы [math]H[/math] размера [math]N\times N[/math] необходимо [math]\;N^2\;[/math] присвоений значений. Из чего можно сделать вывод, что рекурсивный метод построения матрицы Адамара является алгоритмом с квадратичной сложностью.
1.7 Информационный граф
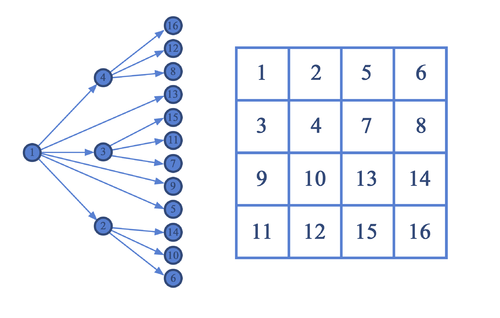
Зависимость данных для матрицы размерностью [math]4*4[/math] можно увидеть на рис.1.
1.8 Ресурс параллелизма алгоритма
Логически алгоритм можно разделить на три части, которые на каждом шаге выполняются независимо. Внутри каждой части происходит [math]2^{2N}-2^{2(N-1)}[/math] независимых присвоений, где [math]N[/math] - номер шага алгоритма, причем размерность матрицы на шаге [math]N[/math] равна [math]2^N[/math]. При этом необходимо ждать завершения предыдущего шага, то есть необходимы синхронизирующие блокировки.
1.9 Входные и выходные данные алгоритма
Входные данные: [math]N[/math] - размерность матрицы.
Объем входных данных: 1.
Выходные данные: матрица размером [math]N\times N[/math].
Объем выходных данных: [math] N^2[/math].
1.10 Свойства алгоритма
Алгоритм полностью детерминирован.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Реализация MATLAB
Реализация PYTHON
Реализация WOLFRAM
На языке Java реализован класс Hadamard не входящий в стандарт языка. С кодом можно ознакомиться по ссылке.
3 Литература
1. Мак-Вильямс Ф., Слоэн Н. — "Теория кодов, исправляющих ошибки" (1979)
2. Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — "Алгебраический аппарат квантовой информатики 2"
3. М. Н. Аршинов, Л. Е. Садовский — "Коды и математика" (1983)