Участник:IanaV/Алгоритм k means: различия между версиями
IanaV (обсуждение | вклад) |
IanaV (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | + | {{Assignment}} | |
| + | {{Assignment|Zhum}} | ||
{{level-a}} | {{level-a}} | ||
Версия 21:41, 15 ноября 2016
 | Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 15.11.2016 Авторы этой статьи считают, что задание выполнено. |
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 15.11.2016 Данная работа соответствует формальным критериям. Проверено Zhum. |
Авторы страницы: Валуйская Я.А., Глотов Е.С.
Вклад в основную часть работы (сбор и анализ данных) у авторов одинаков, четких разграничений по пунктам статьи сделать невозможно. Итоговое оформление статьи выполнила Валуйская Я.А.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм k-means (k средних) - один из наиболее популярных алгоритмов кластеризации. Наиболее простой, но в то же время достаточно неточный метод кластеризации в классической реализации.
Алгоритм был разработан в 1956 году математиком Гуго Штейнгаузом [1], и почти одновременно его изобрел Стюарт Ллойд [2]. Особую популярность алгоритм снискал после работы Джеймса Маккуина [3]
Алгоритм кластеризации k-means решает задачу распределения [math]N[/math] наблюдений (элементов векторного пространства) на заранее известное число кластеров [math]K[/math]. Действие алгоритма таково, что он стремится минимизировать среднеквадратичное отклонение на точках каждого кластера.
Алгоритм k-means является итерационным алгоритмом кластеризации. На каждой итерации происходит пересчет центра масс для каждого кластера, полученного на предыдущем шаге, затем исходные векторы заново распределяются по кластерам в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике. Алгоритм завершается, когда на какой-то итерации не происходит изменения кластеров.
1.2 Математическое описание алгоритма
Исходные данные:
- множество наблюдений [math]X = \{x_1, x_2, ..., x_n\}[/math], где каждое наблюдение [math]x_i \in R^d, i = 1, ..., n[/math];
- количество кластеров [math]k \in N, k \leq n[/math]
Обозначения:
- [math]S = \{S_1, S_2, ..., S_k \} [/math] - множество кластеров, которые удовлетворяют следующим условиям:
- [math]S_i \bigcap S_j = \emptyset, i \neq j[/math];
- [math]X = {\bigcup \limits _{i = 1}^k S_i} [/math].
- [math]\mu_i \in R^d, i = 1, ..., k[/math] - центр масс кластера [math]S_i[/math]
- [math]d(u, v)[/math] - расстояние между векторами [math]u \in R^m, v \in R^m[/math]
Выходные данные:
- [math]L = (l_1, l_2, ..., l_n)[/math] - набор меток, где метка [math]l_i \in N_{[1, k]}[/math] - является порядковым номером кластера, к которому принадлежит вектор [math]x_i[/math]: [math] x_i \in S_{l_i}[/math]
Цель алгоритма k-means - распределить наблюдения из входного множества [math]X[/math] по [math]k[/math] кластерам [math]S = \{S_1, S_2, ..., S_k \} [/math] таким образом, чтобы сумма квадратов расстояний от каждой точки кластера до его центра масс по всем кластерам была минимальной:
[math]\arg\min_{S} \sum_{i=1}^{k} \sum_{x \in S_i} (d(x, \mu_i))^2 [/math],
Алгоритм состоит из следующих шагов:
- Инициализация центров масс
На данном шаге задаются начальные значения центров масс [math] \mu_1^1, ..., \mu_k^1[/math]. Существует несколько способов их выбора. Они будут рассмотрены ниже. - t-ый шаг итерации:
- Распределение векторов по кластерам
На данном шаге каждый вектор [math]x_i \in X[/math] распределяется в свой кластер [math]S_j^t[/math] так, что:
[math]l_i^t = \arg \min_{j} (d(x_i, \mu_j^t))^2 , j = 1, ..., k; i = 1, ..., n[/math] - Пересчет центров масс кластеров
На данном шаге происходит пересчет центров масс кластеров, полученных на предыдущем этапе:
[math]\mu_i^{t+1} = \frac{1}{|S_i^t|} \sum_{x \in S_i^t} x[/math]; [math]i = 1, ..., k[/math]
- Распределение векторов по кластерам
- Критерий останова
[math]\mu_i^t = \mu_i^{t+1},[/math] для всех [math]i = 1, ..., k[/math]
Способы инициализации начальных данных:
- Метод Forgy
Случайным образом выбираются [math]k[/math] векторов из множества наблюдений [math]X[/math]. Эти вектора используются в качестве центров масс кластеров [math]\mu_1, ..., \mu_k[/math] - Метод случайного разбиения (Random Partition) [4]
Каждый вектор [math]x_i, i = 1, .., n[/math] случайным образом распределяется в кластер [math]S_j, j = 1, .., k[/math], затем для каждого кластера вычисляется его центр масс [math]\mu_j[/math].
1.3 Вычислительное ядро алгоритма
Вычислительном ядром алгоритма является шаг 2, состоящий из следующих этапов:
- распределение векторов по кластерам;
- пересчет центров масс кластеров.
Распределение векторов по кластерам заключается в следующем: для каждого вектора [math]x_i \in X, i = 1, ..., n[/math] необходимо посчитать расстояние между этим вектором и центром масс кластера [math]\mu_j^t, j = 1, ..., k[/math]. Следовательно, на каждой итерации необходимо выполнить [math]n * k[/math] операций вычисления расстояния между векторами.
Пересчет центров масс кластеров заключается в следующем: для каждого кластера [math]S_i^t \in S, i = 1, ..., k[/math] необходимо пересчитать кластер по формуле, приведенной в пункте выше. Следовательно, на каждой итерации необходимо выполнить [math]k[/math] операций пересчета центров масс кластеров.
1.4 Макроструктура алгоритма
- Макрооперация "Расстояние между векторами"
В данном алгоритме используется Евклидова метрика:
[math]v \in R^m[/math] и [math]u \in R^m: d(v, u) = \sqrt{\sum_{j=1}^{m} (v_j - u_j)^2} [/math]; - Макрооперация "Пересчет центра масс кластера"
[math]\mu_i^{t+1} = \frac{1}{|S_i^t|} \sum_{x \in S_i^t} x[/math]
Таким образом, алгоритм в терминах макроопераций выглядит следующим образом:
- Инициализация центров масс
Метод Forgy: центры масс [math]\mu_j^1, j = 1, ..., k[/math] выбираются случайным образом.
Метод случайного разбиения: вектора [math]x_i \in X[/math] случайным образом распределяются по кластерам. Для каждого кластера выполняется макрооперация "Пересчет центра масс кластера" для нахождения [math]\mu_j^1[/math].
- t-ый шаг итерации:
- Распределение векторов по кластерам
На данном шаге для каждого вектора [math]x_i \in X[/math] k раз выполняется макрооперация "Расстояние между векторами" для нахождения расстояния между [math]x_i[/math] и [math]\mu_j^t, j = 1, ..., k[/math]. Затем для каждого вектора [math]x_i[/math] находится минимальное расстояние. - Пересчет центров масс кластеров
На данном шаге для каждого кластера выполняется макрооперация "Пересчет центра масс" для нахождения [math]\mu_j^{t+1}[/math].
- Распределение векторов по кластерам
- Критерий останова
[math]\mu_i^t = \mu_i^{t+1},[/math] для всех [math]i = 1, ..., k[/math]
1.5 Схема реализации последовательного алгоритма
Псевдокод алгоритма:
Входные данные : Множество векторов [math]X[/math], количество кластеров [math]k[/math] Выходные данные : Набор меток [math]L[/math] принадлежности к кластеру 1 Инициализация центров масс [math]\mu_i^1, i = 1, ..., k[/math]; 2 t := 1; 3 Для каждого вектора [math]x_i \in X, i = 1, ..., n:[/math] [math]l_i^t = \arg \min_{j} (d(x_i,\mu_j^t))^2 , j = 1, ..., k[/math]; 4 Для каждого кластера [math]S_i^t, i = 1, ..., k[/math] выполняется макрооперация "Пересчет центра масс"; 5 if ([math]\exists i = 1, ..., k: \mu_i^t \neq \mu_i^{t+1}[/math]) { 6 t := t + 1; 7 goto 3; 8 } else { 9 stop; 10 };
Существующие способы оптимизации алгоритма [5] [6] [7]
1.6 Последовательная сложность алгоритма
Подсчитаем количество операций для каждого шага алгоритма.
- Инициализация:
- Метод Forgy: [math]N_{init} = 0[/math]
- Метод случайного разбиения:
- Количество операций деления: [math]N^{/}_{init} = k * d[/math];
- Количество операций сложения: [math]N^{+}_{init} = d * (n - k)[/math].
- Распределение [math]n[/math] векторов [math]x_i \in R^d[/math] по [math]k[/math] кластерам на одной итерации:
- Количество операций умножения: [math]N^{*}_{distr} = k * n * d[/math];
- Количество операций сложения: [math]N^{+}_{distr} = k * n * (d - 1)[/math];
- Количество операций вычитания: [math]N^{-}_{distr} = k * n * d[/math];
- Количество операций взятия минимума: [math]N^{min}_{distr} = n * (k - 1)[/math].
- Пересчет центра масс [math]\mu_i \in R^d[/math] для [math]k[/math] кластеров на одной итерации:
- Количество операций деления: [math]N^{/}_{update} = k * d[/math];
- Количество операций сложения: [math]N^{+}_{update} = d * (n - k)[/math].
Следовательно, в случае если алгоритм сошелся за [math]i[/math] итераций, получаем:
- Операций сложения/вычитания: [math]N^{+,-}_{k-means} = N^{+}_{init} + i*(N^{+}_{distr} + N^{-}_{distr} + N^{+}_{update}) = d * (n - k) + i*(k*n*(d-1)+k*n*d+d*(n-k)) \thicksim O(i*k*n*d)[/math]
- Операций умножения/деления: [math]N^{*,/}_{k-means} = N^{/}_{init} + i*(N^{*}_{distr} + N^{/}_{update}) = k * d + i*(k*n*d+k*d) \thicksim O(i*k*n*d)[/math]
Таким образом, последовательная сложность алгоритма k-means для [math]n[/math] [math]d[/math]-мерных векторов и [math]k[/math] кластеров за [math]i[/math] итераций, требуемых для сходимости алгоритма:
[math]O(i * n * k * d)[/math]
1.7 Информационный граф
Рассмотрим информационный граф алгоритма k-means. На рисунке 1 представлена общая схема алгоритма k-means, согласно разделу "Схема реализации последовательного алгоритма". Вершина Init - этап инициализации. Вершина Distribute - этап распределения векторов по кластерам. Вершина Update - этап пересчета центров масс кластеров.
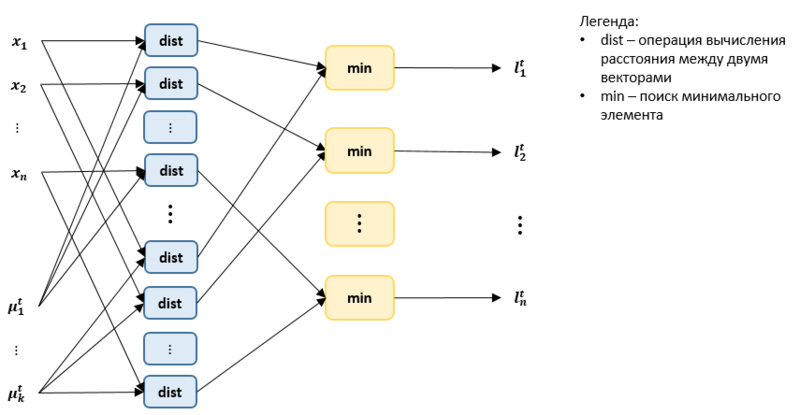
На рисунке 2 представлен информационный граф этапа распределения векторов по кластерам. На вход данному этапу подают множество векторов [math]x_1, x_2, ..., x_n[/math] из входных данных и множество центров масс кластеров [math]\mu^t_1, ..., \mu^t_k[/math], полученных с шага инициализации или с предыдущей итерации. Для каждой пары векторов [math]x_i, \mu^t_j, i = 1, ..., n; j = 1,..., k[/math] считается расстояние между ними (вершина dist). Информационный граф вычисления расстояния между двумя векторами рассмотрен ниже (рисунок 3). Затем выполняется операция нахождения минимума (вершина min), в результате которой каждому вектору [math]x_i, i = 1, ..., n[/math] приписывается метка [math]l^t_i[/math], равная порядковому номеру кластера [math]S^t_j, j = 1 ..., k[/math], которому принадлежит данный вектор: [math]x_i \in S^t_j[/math].
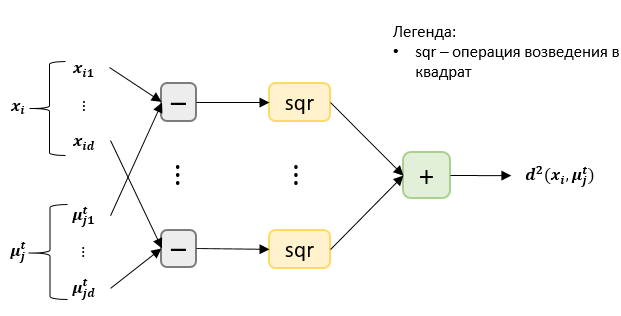
На рисунке 3 представлен информационный граф вычисления расстояния между двумя векторами [math]x_i = (x_{i1}, ..., x_{id}), i = 1, ..., n[/math] и [math]\mu^t_j = (\mu^t_{j1}, ..., \mu^t_{jd}) , j = 1, ..., k[/math]. Выполняется операция поэлементного вычитания двух векторов (вершины -), затем возведение в квадрат (вершины sqr), затем суммирование полученных результатов (вершина +). На выходе получаем квадрат расстояния между векторами.
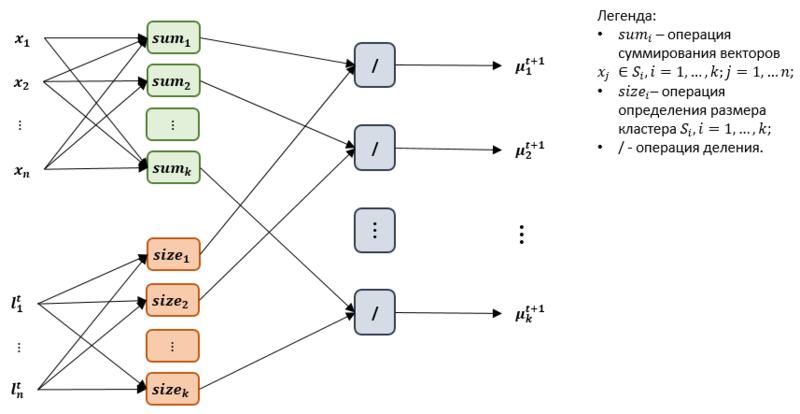
На рисунке 4 представлен информационный граф этапа пересчета центров масс кластеров [math]\mu^t_1, \mu^t_2,..., \mu^t_k[/math]. Для каждого кластера [math]S^t_j, j = 1, ..., k[/math] выполняется операция суммирования (вершина [math]sum_j[/math]) векторов, которые принадлежат данному кластеру. Кроме того, для каждого кластера выполняется операция определения количества элементов в нем (вершина [math]size_j[/math]). Затем выполняется операция деления (вершина /). На выходе получаем новые центры масс кластеров [math]\mu^{t+1}_1, \mu^{t+1}_2,..., \mu^{t+1}_k[/math].
1.8 Ресурс параллелизма алгоритма
Вычислительное ядро алгоритма имеет большие возможности для параллелизма:
- Распределение векторов по кластерам: вектора [math]x_i, x_j, i \neq j; i, j = 1, ..., n[/math] могут быть распределены по кластерам независимо друг от друга;
- Пересчет центров масс кластеров: центры масс кластеров [math]\mu_i, \mu_j, i \neq j; i, j = 1, ..., k[/math] могут быть пересчитаны независимо друг от друга.
Однако, этап пересчета центров масс кластеров зависит от этапа распределения векторов по кластерам, так что эти этапы должны выполняться строго последовательно. Таким образом, параллельная сложность алгоритма может быть вычислена следующим образом:
[math]N_{k-means} = i * (N_{distr} + N_{update})[/math], где [math]i[/math] - количество итераций, необходимых для сходимости алгоритма, [math]N_{distr}[/math] - параллельная сложность этапа распределения векторов по кластерам, [math]N_{update}[/math] - параллельная сложность этапа пересчета центров масс кластеров.
Рассчитаем параллельную сложность [math]N_{distr}[/math] этапа распределения векторов по кластерам в предположении наличия неограниченного числа процессоров для одной итерации. Для каждой пары векторов [math](x_i, \mu_j), i = 1,...,n; j = 1, ..., k[/math] операция вычисления расстояния выполняется независимо.
- При выполнении операция вычисления расстояния операции вычитания и умножения выполняются независимо друг от друга, поэтому требуется только одно вычитание и одно умножение. Число операций сложения: [math]N^{+}_{distr} = O(log(d))[/math] согласно алгоритму нахождения частичной суммы элементов массива путем сдваивания;
- Для нахождения минимума среди [math]k[/math] элементов требуется [math]O(log(k))[/math] операций сравнения.
Таким образом, получаем, что [math]N_{distr} = O(log(k*d))[/math]
Рассчитаем параллельную сложность [math]N_{update}[/math] этапа пересчета центров масс кластеров в предположении наличия неограниченного числа процессоров для одной итерации. Нахождение центра масс [math]\mu_j, j = 1, ..., k[/math] кластера [math]S_j[/math] может выполняться независимо от нахождения центров масс других кластеров. Таким образом, получаем, что [math]N_{update} \leq O(log(n))[/math] в худшем случае, когда почти все векторы находятся в одном кластере.
Итоговая параллельная сложность алгоритма:
[math]N_{k-means} \leq i * (log(k*d) + log(n)) \thicksim O(i * log(k*d*n)); i[/math] - количество итераций, необходимых для сходимости.
1.9 Входные и выходные данные алгоритма
Входные данные:
- [math]n[/math] векторов [math]x_i \in R^d, i = 1, ..., n[/math];
- число кластеров [math]k \in N_{[1,n]}[/math].
Объем входных данных: [math]n * d[/math] действительных чисел, 1 целое положительное число
Выходные данные:
- вектор меток [math]L \in N^n[/math].
Объем выходных данных: [math]n[/math] целых неотрицательных чисел.
1.10 Свойства алгоритма
- Достоинства
- Алгоритм прозрачный и понятный, за счет чего очень прост в реализации;
- Алгоритм имеет высокую скорость работы в случае выбора оптимальных начальных значений центров масс кластеров.
- Недостатки
- Число кластеров является входным аргументом алгоритма. Таким образом, некорректный выбор данного параметра может привести к плохим результатам работы алгоритма, поэтому зачастую проводят несколько прогонов алгоритма с разными значениями [math]k[/math], чтобы подобрать оптимальный;
- Алгоритм может сойтись к локальному минимуму (достижение глобального минимума не гарантируется);
- Результат сильно зависит от выбора начальных значений центров масс кластеров. Существует улучшенная версия алгоритма - k-means++ [8], которая предлагает свой способ нахождения начальных оптимальных значений центров масс кластеров;
- Чувствительность к выбросам и шумам, так как они учитываются при вычислении центров масс кластеров.
- Устойчивость
- Алгоритм является устойчивым к погрешностям во входных данных, так как при вычислении центров кластеров расстояния между объектами усредняются, что приводит к уменьшению ошибки. Алгоритм также является устойчивым к погрешностям, допускаемых при вычислениях, так как операция сложения на каждой новой итерации выполняется над входными данными.
- Сбалансированность
Множество входных векторов можно равномерно разделить между параллельными вычислителями. Центры всех кластеров можно распространить на все вычислители (так как их заведомо меньше, чем число входных векторов). В таком случае на каждой итерации определение для каждого объекта ближайшего кластера представляет собой вычисление расстояния от каждого входного вектора, находящегося на вычислителе, до каждого кластера, и является сбалансированной операцией. После данного этапа происходит пересчёт центров кластеров. Данная операция является несбалансированной в случаях, когда число объектов в одном из кластеров значительно больше числа объектов в других кластерах, из-за чего один кластер занимает большое число вычислителей, а остальные занимают по одному или несколько вычислителей. В таком случае для данного кластера потребуется вычислить центр алгоритмом нахождения частичной суммы элементов массива путем сдваивания. Данная операция представляет несбалансированность порядка [math]O(log (k*n))[/math]. После данного шага происходит сбалансированная операция рассылки центров кластеров на все вычислители.
В идеальном случае параллелизации алгоритм не является сбалансированным, однако в реальных задачах, когда [math]n \gt \gt p[/math], где [math]p[/math] - количество вычислителей, эта несбалансированность сглаживается наличием объектов из каждого кластера на каждом вычислителе
- Соотношение последовательной и параллельной сложности
- [math]{O(n*d*k*i) \over O(log(n*d*k)*i)} \thicksim O \bigg( {n*d*k \over log(n*d*k)} \bigg)[/math]
- Вычислительная мощность
Последовательный алгоритм: [math]{O(n*d*k*i) \over n*d+n+1} \thicksim {O(d*k*i) \over d+1} \thicksim O(k*i)[/math], где [math]n[/math] - число входных векторов, [math]d[/math] - размерность векторов, [math]k[/math] - число кластеров, [math]i[/math] - число итераций, требуемое для сходимости
Параллельный алгоритм: [math]O(log(n*d*k)*i) \over n*d+n+1[/math]
- Детерминированность
- Алгоритм является недетерминированным, так как результат зависит от выбора исходных центров кластеров, а их оптимальный выбор неизвестен.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса МГУ им. М.В. Ломоносова.
Набор данных для тестирования состоял из 946000 векторов размерности 2 (координаты на сфере)
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессов (виртуальных ядер) [8 : 512];
- число кластеров [128 : 384].
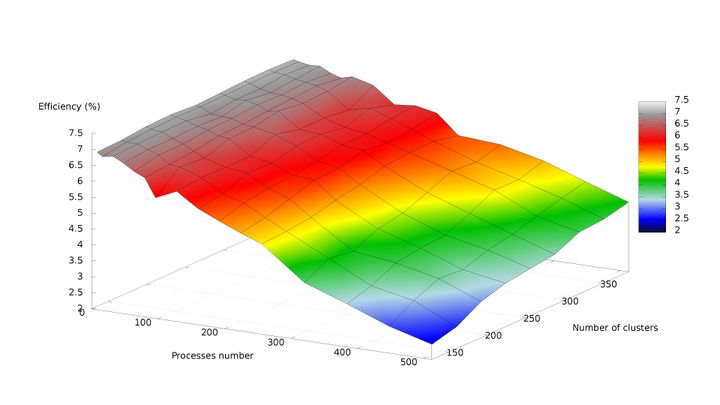
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации [math]2,47%[/math] достигается при делении исходных данных на 128 кластеров с использованием 512 процессов;
- максимальная эффективность реализации [math]7,13%[/math] достигается при делении исходных данных на 352 кластера с использованием 8 процессов.
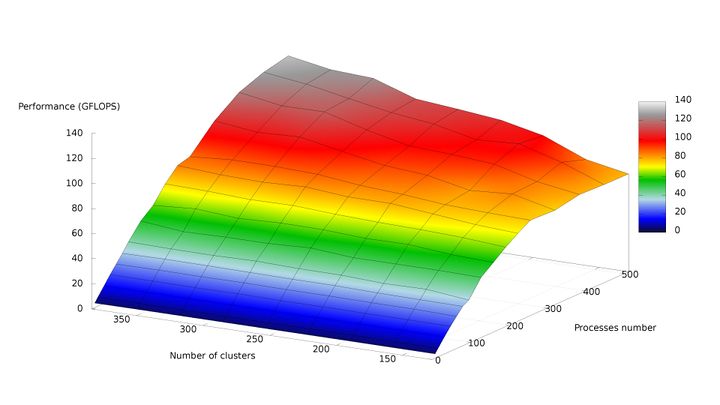
На следующих рисунках приведены графики производительности и эффективности выбранной реализации k means в зависимости от изменяемых параметров запуска.
Исследовалась параллельная реализация алгоритма k means. Для вычисления производительности в неё был вписан код на MPI, реализующий подсчёт числа операций с плавающей точкой.
Были получены следующие оценки масштабируемости реализации алгоритма k means:
- По числу процессов: [math]-0.02209[/math]. Следовательно, с ростом числа процессов эффективность уменьшается.
- По размеру задачи: [math]0.01252[/math]. Следовательно, с ростом размера задачи (числа кластеров) эффективность увеличивается.
- Общая оценка: [math]-0.00081[/math]. Таким образом, с ростом и размера задачи, и числа процессов эффективность уменьшается.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существуют следующие Open Source реализации алгоритма:
- ELKI - содержит реализацию алгоритма k-means на языке Java (в том числе реализацию улучшенного алгоритма k-means++)
- Weka - содержит реализацию k-means на языке Java
- Apache Mahout - содержит реализацию k-means в парадигме MapReduce
- Spark Mllib - содержит распределенную реализацию k-means
- Accord.NET - содержит реализацию k-means на C# (в том числе реализацию улучшенного алгоритма k-means++)
- MLPACK - содержит реализацию k-means на языке C++
- OpenCV - содержит реализацию k-means на C++. А также есть обертки для языков Python и Java
- SciPy - содержит реализацию k-means на языке Python
- Scikit-learn - содержит реализацию k-means на языке Python
- Julia - содержит реализацию алгоритма k-means на языке Julia
- Octave - содержит реализацию k-means на языке Octave
- R - содержит реализацию k-means на языке R
- Torch - содержит реализацию k-means на языке Lua
3 Литература
- ↑ Steinhaus H. (1956). Sur la division des corps materiels en parties. Bull. Acad. Polon. Sci., C1. III vol IV: 801—804.
- ↑ Lloyd S. (1957). Least square quantization in PCM’s. Bell Telephone Laboratories Paper.
- ↑ MacQueen J. (1967). Some methods for classification and analysis of multivariate observations. In Proc. 5th Berkeley Symp. on Math. Statistics and Probability, pages 281—297.
- ↑ Hamerly, G.; Elkan, C. (2002). "Alternatives to the k-means algorithm that find better clusterings". Proceedings of the eleventh international conference on Information and knowledge management (CIKM).
- ↑ Phillips S. J. Acceleration of k-means and related clustering algorithms //Workshop on Algorithm Engineering and Experimentation. – Springer Berlin Heidelberg, 2002. – С. 166-177.
- ↑ Hamerly G. Making k-means Even Faster //SDM. – 2010. – С. 130-140.
- ↑ Elkan C. Using the triangle inequality to accelerate k-means //ICML. – 2003. – Т. 3. – С. 147-153.
- ↑ Arthur, D.; Vassilvitskii, S. (2007). "k-means++: the advantages of careful seeding". Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA. pp. 1027–1035.