Участник:D.Polykovskiy/Алгоритм Бойера-Ватсона: различия между версиями
| (не показано 11 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | Алгоритм '''Бойера–Ватсона''' | + | Алгоритм '''Бойера–Ватсона''' - метод, позволяющий построить триангуляцию Делоне конечного множества точек в пространстве любой размерности. Как следствие, алгоритм позволяет получить диаграму Вороного. |
= Свойства и структура алгоритма = | = Свойства и структура алгоритма = | ||
| Строка 10: | Строка 10: | ||
Итерации алгоритма строятся следующим образом: | Итерации алгоритма строятся следующим образом: | ||
| − | На нулевой итерации строится треугольник ( | + | На нулевой итерации строится треугольник (супер-треугольник), покрывающий все точки множества (таким образом множество S пополняется тремя вспомогательными точками). Начальное множество треугольников состоит только из этого треугольника. |
Далее итеративно выполняются следующие действия: | Далее итеративно выполняются следующие действия: | ||
<ol> | <ol> | ||
| Строка 22: | Строка 22: | ||
<gallery> | <gallery> | ||
| − | File:Bowyer-Watson 0.png|Помещение первой вершины в охватывающий | + | File:Bowyer-Watson 0.png|Помещение первой вершины в охватывающий супер-треугольник |
File:Bowyer-Watson 1.png|Вторая вершина | File:Bowyer-Watson 1.png|Вторая вершина | ||
File:Bowyer-Watson 2.png|Третья вершина | File:Bowyer-Watson 2.png|Третья вершина | ||
File:Bowyer-Watson 3.png|Четвертая вершина | File:Bowyer-Watson 3.png|Четвертая вершина | ||
File:Bowyer-Watson 4.png|Пятая вергина | File:Bowyer-Watson 4.png|Пятая вергина | ||
| − | File:Bowyer-Watson 6.png|Убираем вершины | + | File:Bowyer-Watson 6.png|Убираем вершины супер-треугольника. |
</gallery> | </gallery> | ||
==Вычислительное ядро алгоритма== | ==Вычислительное ядро алгоритма== | ||
| − | Большая часть времени работы алгоритма приходится на поиск поврежденных треугольников. В простейшей реализации это делается за | + | Большая часть времени работы алгоритма приходится на поиск поврежденных треугольников. В простейшей реализации это делается за <math>O(|S|)</math>, однако эта сложность может быть в среднем уменьшена до <math>O(log|S|)</math> при структурировании пространства (например, KD-деревом). Тем не менее в худшем случае поиск все равно будет требовать <math>O(|S|)</math> действий. |
==Макроструктура алгоритма== | ==Макроструктура алгоритма== | ||
===Проверка на вхождение в описанную окружность=== | ===Проверка на вхождение в описанную окружность=== | ||
| − | Для работы алгоритма требуется уметь проверять точку D на принадлежность описанной окружности треугольника ABC. Для двумерного случая это может быть сделано при помощи перехода в 3D пространство по схеме | + | Для работы алгоритма требуется уметь проверять точку D на принадлежность описанной окружности треугольника ABC. Для двумерного случая это может быть сделано при помощи перехода в 3D пространство по схеме <math>(x, y) \to (x, y, x^2+y^2)</math><ref>Leonidas J. Guibas, Jorge Stolfi Primitives for the manipulation of general subdivisions and the computation of Voronoi, ACM Transactions on Graphics </ref> |
| − | В новом пространстве точке расположены на параболоиде. Утверждается, что четыре точки коцикличны в | + | В новом пространстве точке расположены на параболоиде. Утверждается, что четыре точки коцикличны в <math>(x, y)</math> тогда и только тогда, когда они компланарны в пространстве <math>(x, y, x^2+y^2)</math>. Пользуясь выпуклостью парабалоида, можно сформулировать критерий принадлежности точки описанной окружности: достаточно проверить неотрицательность определителя матрицы (предполагается, что точки расположены против часовой стрелки) |
: <math>\begin{vmatrix} | : <math>\begin{vmatrix} | ||
| Строка 50: | Строка 50: | ||
</math> | </math> | ||
| − | ===Построение | + | ===Построение супер-треугольника=== |
| − | Построить | + | Построить супер-треугольник можно множеством способов. Например, можно найти разброс (''max-min'') значений координат точек вдоль каждой из осей. Затем можно вычислить максимальное среди этих значений, обозначив его за ''w''. После этого можно взять центр масс точек ''S'' и отступить от него вверх на ''2w'' (точка A), вниз на 2w и влево на 2w (точка B) и, наконец, вниз на 2w и вправо на 2w (точка C). Треугольник ABC будет заведомо содержать все точки из ''S''. |
===Поиск границы объединения треугольников=== | ===Поиск границы объединения треугольников=== | ||
| Строка 62: | Строка 62: | ||
// pointList - множество точек для триангуляции | // pointList - множество точек для триангуляции | ||
triangulation := пустое множество треугольников | triangulation := пустое множество треугольников | ||
| − | Добавляем | + | Добавляем супер-треугольник в триангуляцию |
for each point in pointList do // последовательно добавляем точки | for each point in pointList do // последовательно добавляем точки | ||
badTriangles := empty set | badTriangles := empty set | ||
| Строка 78: | Строка 78: | ||
newTri := form a triangle from edge to point | newTri := form a triangle from edge to point | ||
add newTri to triangulation | add newTri to triangulation | ||
| − | for each triangle in triangulation // убираем вершины | + | for each triangle in triangulation // убираем вершины супер-треугольника |
if triangle contains a vertex from original super-triangle | if triangle contains a vertex from original super-triangle | ||
remove triangle from triangulation | remove triangle from triangulation | ||
| Строка 85: | Строка 85: | ||
==Последовательная сложность алгоритма== | ==Последовательная сложность алгоритма== | ||
| − | В среднем число поврежденных треугольников оказывается малым, поэтому все действия кроме поиска выполняются в среднем за | + | В среднем число поврежденных треугольников оказывается малым, поэтому все действия кроме поиска выполняются в среднем за <math>O(1)</math>. |
| − | В худшем случае вне зависимости от использования структурирования пространства получается сложность | + | В худшем случае вне зависимости от использования структурирования пространства получается сложность <math>O(|S|^2)</math>. Однако средняя оценка при структурировании снижается до <math>O(|S| log|S|)</math>. |
| + | |||
| + | ==Информационный граф== | ||
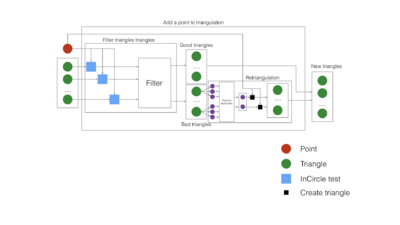
| + | Информационный граф рассматриваемого алгоритма получается напрямую из его описания: | ||
| + | [[Файл:BW.png|thumb|center|400px]] | ||
| + | ==Ресурс параллелизма алгоритма== | ||
| + | Самая трудоемкая часть алгоритма поиск поврежденных треугольников. Это действие можно распараллелить, проводя проверку на повреждение параллельно для каждого треугольника. Поиск дублирующихся ребер также можно распараллелить, однако эта часть программы не являются ресурсоемкой: количество поврежденных треугольников редко бывает большим. | ||
| + | |||
| + | ==Входные и выходные данные алгоритма== | ||
| + | Входными данными алгоритма служит вектор точек пространства. Предполагается, что все точки различны. На выходе получается вектор троек координат вершин треугольников, образующих триангуляцию исходного множества. | ||
| + | |||
| + | ==Свойства алгоритма== | ||
| + | |||
| + | =Программная реализация алгоритма= | ||
| + | ==Особенности реализации последовательного алгоритма== | ||
| + | ==Локальность данных и вычислений== | ||
| + | ==Возможные способы и особенности параллельной реализации алгоритма== | ||
| + | |||
| + | |||
| + | |||
| + | ==Масштабируемость алгоритма и его реализации== | ||
| + | |||
| + | Проведём исследование масштабируемости параллельной реализации алгоритма Бойера-Ватсона. Исследование проводилось на суперкомпьютере "Ломоносов"<ref name="Lom">Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.</ref> [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета]. | ||
| + | |||
| + | Запустим реализацию на различных наборах точек и различном числе нитей (по логарифмической сетке), запросив 16 ядер Intel Xeon X5570. | ||
| + | |||
| + | Полученный график сильной масштабируемости приведен ниже. | ||
| + | |||
| + | [[File:BW_run.png]] | ||
| + | |||
| + | Видно, что при увеличении количества нитей, время работы постепенно снижается, однако когда число нитей превышает удвоенное число запрошенных ядер, эффективность реализации снижается. Это происходит из-за нарастающих накладных расходов на параллелизм. Эффект падения эффективности при 32 процессорах и числе точек 2704 связан с особенностью структуры точек: требовался многократный пересчет поврежденных треугольников. | ||
| + | |||
| + | ==Динамические характеристики и эффективность реализации алгоритма== | ||
| + | |||
| + | ==Выводы для классов архитектур== | ||
| + | |||
| + | ==Существующие реализации алгоритма== | ||
| + | Реализации данного алгоритма не присутствуют в популярных пакетах. Тем не менее, существует несколько доступных реализаций на github: | ||
| + | <ul> | ||
| + | <li>https://github.com/axelboc/voronoi-delaunay</li> | ||
| + | <li>https://github.com/ayron/delaunay</li> | ||
| + | <li>https://github.com/Bl4ckb0ne/delaunay-triangulation</li> | ||
| + | </ul> | ||
| + | |||
| + | =Литература= | ||
| + | <ref>C.A.Arens The Bowyer-Watson algorithm: An efficient implementation in a database environment</ref> | ||
Текущая версия на 14:50, 26 ноября 2016
Алгоритм Бойера–Ватсона - метод, позволяющий построить триангуляцию Делоне конечного множества точек в пространстве любой размерности. Как следствие, алгоритм позволяет получить диаграму Вороного.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Бойера–Ватсона позволяет построить триангуляцию Деолне конечного множества точек в пространстве любой размерности. Он относится к семейству инкрементальных, т.е. проводит построение путем поочередного добавления точек, получая при этом на каждом шаге корректную триангуляцию Делоне текущего подмножества точек.
1.2 Математическое описание алгоритма
Триангуля́ция Делоне́ — триангуляция заданного множества точек S на плоскости (или в пространстве большей размерности), при которой для любого треугольника все точки из S за исключением точек, являющихся его вершинами, лежат вне окружности, описанной вокруг треугольника. На многомерный случай алгоритм обобщается путем замены треугольников на многомерные симплексы.
Итерации алгоритма строятся следующим образом: На нулевой итерации строится треугольник (супер-треугольник), покрывающий все точки множества (таким образом множество S пополняется тремя вспомогательными точками). Начальное множество треугольников состоит только из этого треугольника. Далее итеративно выполняются следующие действия:
- Добавляется новая точка
- Из множества треугольников выкидываются все треугольники, в описанную окружность в которых попадает новая точка. Таким образом в триангуляции образуется дырка в форме многоугольника.
- Эта дырка заполняется треугольниками, содержащими новую точку в качестве одной вершины и ребрами дырки в качестве противолежащей стороны.
Доказано, что после завершения каждой итерации будет получена корректная триангуляция Делоне.
На последнем шаге алгоритма выкидываются треугольники, содержащие в качестве вершины вспомогательную.
1.3 Вычислительное ядро алгоритма
Большая часть времени работы алгоритма приходится на поиск поврежденных треугольников. В простейшей реализации это делается за [math]O(|S|)[/math], однако эта сложность может быть в среднем уменьшена до [math]O(log|S|)[/math] при структурировании пространства (например, KD-деревом). Тем не менее в худшем случае поиск все равно будет требовать [math]O(|S|)[/math] действий.
1.4 Макроструктура алгоритма
1.4.1 Проверка на вхождение в описанную окружность
Для работы алгоритма требуется уметь проверять точку D на принадлежность описанной окружности треугольника ABC. Для двумерного случая это может быть сделано при помощи перехода в 3D пространство по схеме [math](x, y) \to (x, y, x^2+y^2)[/math][1] В новом пространстве точке расположены на параболоиде. Утверждается, что четыре точки коцикличны в [math](x, y)[/math] тогда и только тогда, когда они компланарны в пространстве [math](x, y, x^2+y^2)[/math]. Пользуясь выпуклостью парабалоида, можно сформулировать критерий принадлежности точки описанной окружности: достаточно проверить неотрицательность определителя матрицы (предполагается, что точки расположены против часовой стрелки)
- [math]\begin{vmatrix} A_x & A_y & A_x^2 + A_y^2 & 1\\ B_x & B_y & B_x^2 + B_y^2 & 1\\ C_x & C_y & C_x^2 + C_y^2 & 1\\ D_x & D_y & D_x^2 + D_y^2 & 1 \end{vmatrix} = \begin{vmatrix} A_x - D_x & A_y - D_y & (A_x^2 - D_x^2) + (A_y^2 - D_y^2) \\ B_x - D_x & B_y - D_y & (B_x^2 - D_x^2) + (B_y^2 - D_y^2) \\ C_x - D_x & C_y - D_y & (C_x^2 - D_x^2) + (C_y^2 - D_y^2) \end{vmatrix} \gt 0 [/math]
1.4.2 Построение супер-треугольника
Построить супер-треугольник можно множеством способов. Например, можно найти разброс (max-min) значений координат точек вдоль каждой из осей. Затем можно вычислить максимальное среди этих значений, обозначив его за w. После этого можно взять центр масс точек S и отступить от него вверх на 2w (точка A), вниз на 2w и влево на 2w (точка B) и, наконец, вниз на 2w и вправо на 2w (точка C). Треугольник ABC будет заведомо содержать все точки из S.
1.4.3 Поиск границы объединения треугольников
Эту задачу требуется решить только для связного множества треугольников. Поэтому достаточно взять все ребра треугольников и выкинуть дублирующиеся. Оставшиеся ребра будут образовывать искомый многоугольник.
1.5 Схема реализации последовательного алгоритма
function BowyerWatson (pointList)
// pointList - множество точек для триангуляции
triangulation := пустое множество треугольников
Добавляем супер-треугольник в триангуляцию
for each point in pointList do // последовательно добавляем точки
badTriangles := empty set
for each triangle in triangulation do // находим поврежденные треугольники
if point is inside circumcircle of triangle
add triangle to badTriangles
polygon := empty set
for each triangle in badTriangles do // находим границу дырки
for each edge in triangle do
if edge is not shared by any other triangles in badTriangles
add edge to polygon
for each triangle in badTriangles do // удаляем поврежденные треугольники
remove triangle from triangulation
for each edge in polygon do // заполняем дырку
newTri := form a triangle from edge to point
add newTri to triangulation
for each triangle in triangulation // убираем вершины супер-треугольника
if triangle contains a vertex from original super-triangle
remove triangle from triangulation
return triangulation
1.6 Последовательная сложность алгоритма
В среднем число поврежденных треугольников оказывается малым, поэтому все действия кроме поиска выполняются в среднем за [math]O(1)[/math].
В худшем случае вне зависимости от использования структурирования пространства получается сложность [math]O(|S|^2)[/math]. Однако средняя оценка при структурировании снижается до [math]O(|S| log|S|)[/math].
1.7 Информационный граф
Информационный граф рассматриваемого алгоритма получается напрямую из его описания:
1.8 Ресурс параллелизма алгоритма
Самая трудоемкая часть алгоритма поиск поврежденных треугольников. Это действие можно распараллелить, проводя проверку на повреждение параллельно для каждого треугольника. Поиск дублирующихся ребер также можно распараллелить, однако эта часть программы не являются ресурсоемкой: количество поврежденных треугольников редко бывает большим.
1.9 Входные и выходные данные алгоритма
Входными данными алгоритма служит вектор точек пространства. Предполагается, что все точки различны. На выходе получается вектор троек координат вершин треугольников, образующих триангуляцию исходного множества.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Проведём исследование масштабируемости параллельной реализации алгоритма Бойера-Ватсона. Исследование проводилось на суперкомпьютере "Ломоносов"[2] Суперкомпьютерного комплекса Московского университета.
Запустим реализацию на различных наборах точек и различном числе нитей (по логарифмической сетке), запросив 16 ядер Intel Xeon X5570.
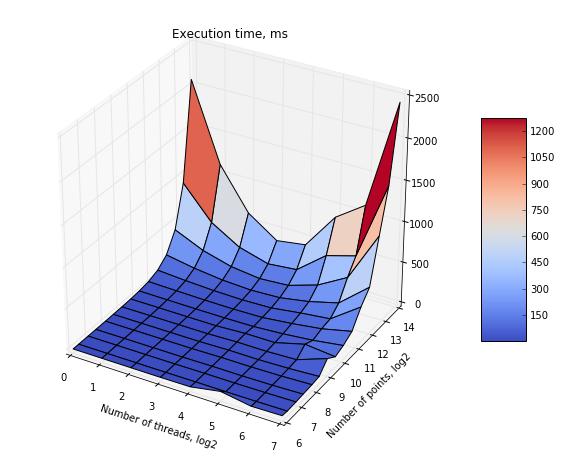
Полученный график сильной масштабируемости приведен ниже.
Видно, что при увеличении количества нитей, время работы постепенно снижается, однако когда число нитей превышает удвоенное число запрошенных ядер, эффективность реализации снижается. Это происходит из-за нарастающих накладных расходов на параллелизм. Эффект падения эффективности при 32 процессорах и числе точек 2704 связан с особенностью структуры точек: требовался многократный пересчет поврежденных треугольников.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Реализации данного алгоритма не присутствуют в популярных пакетах. Тем не менее, существует несколько доступных реализаций на github:
- https://github.com/axelboc/voronoi-delaunay
- https://github.com/ayron/delaunay
- https://github.com/Bl4ckb0ne/delaunay-triangulation
3 Литература
- ↑ Leonidas J. Guibas, Jorge Stolfi Primitives for the manipulation of general subdivisions and the computation of Voronoi, ACM Transactions on Graphics
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.
- ↑ C.A.Arens The Bowyer-Watson algorithm: An efficient implementation in a database environment