Участник:JuliaA/Алгоритм кластеризации с использованием представлений: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
(не показано 157 промежуточных версий 6 участников)
Строка 1: Строка 1:
−
Основные авторы описания: Ю.А. Антохина, С.А. Шатков
+
Основные авторы описания: <br>
 +
[[Участник:JuliaA|Ю.А. Антохина]], разделы [[#Общее описание алгоритма|1.1]], [[#Схема реализации последовательного алгоритма|1.5]], [[#Последовательная сложность алгоритма|1.6]], [[#Ресурс параллелизма алгоритма|1.8]] - [[#Свойства алгоритма|1.10]], [[#Существующие реализации алгоритма|2.7]]<br>
  
−
= ЧАСТЬ. Свойства и структура алгоритмов =
+
[[Участник:Cookie|С.А. Шатков]], разделы [[#Математическое описание алгоритма|1.2]] - [[#Схема реализации последовательного алгоритма|1.5]], [[#Информационный граф|1.7]], [[#Масштабируемость алгоритма и его реализации|2.4]] <br>
 +
 
 +
= Свойства и структура алгоритмов =
 
== Общее описание алгоритма ==
 
== Общее описание алгоритма ==
 +
 +
Пусть дан набор точек и заданы правила определения расстояния между ними. Задача кластеризации сгруппировать эти точки в определенное число кластеров. Члены одного кластера похожи, а члены разных классов различны.
 +
 +
В алгоритме CURE применяется иерархическая кластеризация. Есть два подхода к иерархической кластеризации. В одном случае один большой кластер на каждом шаге разбивается на несколько, пока число кластеров не будет равно заданному заранее числу кластеров. В другом случае наоборот кластеры, состоящие каждый из одной точки объединяются в большие. Второй метод используется в CURE.
 +
 +
Результат кластеризации зависит от того, как будут представлены кластеры. Например, средним всех точек кластера, или всеми точками кластера. Применение среднего возможно только в евклидовом пространстве. А использование всех точек неустойчиво к случайным выбросам. В CURE используется другой метод: для каждого кластера выбираются точки-представители. Выбирается постоянное число точек, которые будут представлять каждый кластер. Кластеры с наиболее похожими наборами репрезентативных точек объединяются на каждом шаге алгоритма.
 +
 +
За счет использования точек-представителей алгоритм CURE устойчив к выбросам и может выделять кластеры сложной формы и различных размеров.
 +
 +
Описание шагов
 +
 +
'''Шаг 1'''. Если все данные использовать сразу как входные для CURE, то эффективность алгоритма будет низкая, а время выполнения большим. Поэтому на первом шаге мы случайным образом выбираем часть точек которые помещаются в память, затем группируем наиболее похожие с помощью иерархического метода в заранее заданное число кластеров.
 +
Дальше работаем с кластерами.
 +
 +
'''Шаг 2'''. Для каждого кластера выбираем <math>c</math> точек-представителей, максимально удаленных друг от друга. Чисто <math>c</math> остается постоянным.
 +
 +
'''Шаг 3'''. Объединяем кластеры с наиболее похожими наборами точек-представителей.
 +
Если не достигнуто нужное число кластеров, то перейти на шаг 2.
 +
Чтобы при объединении кластеров не выбирать каждый раз c точек-представителей из всех точек, мы выбираем их только из <math>2c</math> точек объединенных кластеров.
 +
 +
Выбранные точки сдвигаются на следующем шаге на <math>\alpha</math> к центроиду кластера. Алгоритм становится основанным на методе поиска центроида при <math>\alpha = 1</math>, и основанным на всех точках кластера при <math>\alpha = 0</math>.
 +
 +
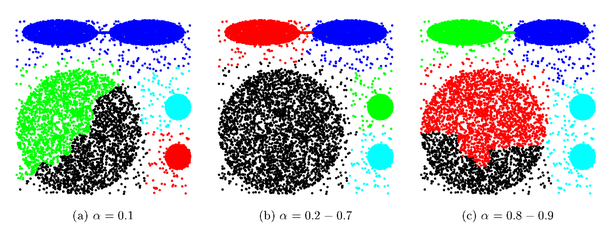
[[Файл:Exampleofalgorithmparametrs1.png|600px|thumb|center|Пример работы алгоритма для разных параметров <math>\alpha</math> [1].]]
  
 
== Математическое описание алгоритма ==
 
== Математическое описание алгоритма ==
 +
 +
Пусть дана матрица <math>x \in R^{m\times n}</math>, количество кластеров <math>h</math>, число точек-представителей <math>c</math>, параметр <math>\alpha</math>, параметр <math>\gamma</math>. Каждая строка матрицы представляет собой точку в <math>n</math> - мерном пространстве.
 +
 +
m число точек для кластеризации, n размерность.
 +
 +
Расстояние <math>\rho(a,b)</math> между точками <math>a = (a_{1},\dots,a_{n})</math> и <math>b = (b_{1},\dots,b_{n})</math> будем вычислять по формуле:
 +
 +
<math>\rho(a,b) = \sqrt{\sum_{i=1}^n (a_{i} - b_{i})^2}</math>
 +
 +
'''Шаг "Инициализация"'''
 +
 +
Выбираются <math>\lceil \gamma m\rceil</math> строк матрицы случайным образом. Например, можно использовать [https://ru.wikipedia.org/wiki/Reservoir_sampling Алгоритм R].
 +
 +
В основной памяти выделяется куча, часть которой используется для размещения дерева, листьями которого являются выбранные строки, соединённые ребром с вершиной дерева.
 +
 +
 +
'''Шаг "Кластеризация"'''
 +
 +
В самом начале шага считаем каждую выбранную точку одноточечным кластером с центроидой в этой же точке.
 +
 +
Далее выполняем следующие шаги 1-2, пока количество кластеров не станет равно <math>h</math>:
 +
 +
Шаг 1:
 +
 +
Для каждого <math>i</math>-го кластера вычисляется центроида <math>\mu_{i}</math> по формуле:
 +
 +
<math>\mu_{i} = \frac{1}{s_{i}}\sum_{j\in S_{i}} x^{j}</math>, где <math>S_{i}</math> - номера строк матрицы <math>x</math>, входящие в <math>i</math>-й кластер; <math>s_{i}</math> - количество элементов в множестве <math>S_{i}</math>; <math>x^{j}</math> - <math>j</math>-я строка матрицы <math>x</math>.
 +
 +
Шаг 2:
 +
 +
Выполняется поиск пары кластеров, "наиболее подходящих" для объединения. В качестве критерия выбора можно рассматривать: наименьшее расстояние между центроидами кластеров или наименьшее расстояние между элементами, входящими в рассматриваемую пару кластеров. Существуют также другие критерии выбора "подходящих" классов, например, сравнение плотности кластеров до объединения и после. Далее выполняется слияние найденных кластеров. Для дерева это означает добавление новой вершины, соединённой ребром с корнем; поддеревья кластеров становятся ветвями этой новой вершины.
 +
 +
 +
'''Шаг "Назначение представителей"'''
 +
 +
На данном шаге для каждого кластера определяются <math>c</math> точек-представителей. Для наилучшего отображения формы множества предполагается использование точек, максимально удалённых друг от друга.
 +
 +
Для этого используем следующий алгоритм:
 +
 +
Пусть <math>i</math> - текущее количество представителей, <math>S_{k}</math> - множество номеров строк матрицы <math>x</math>, входящие в <math>k</math>-й кластер, <math>R_{k}</math> - множество номеров строк матрицы <math>x</math>, назначенных представителями <math>k</math>-го кластера, а <math>x^{j}</math> - вектор-строка матрицы <math>x</math>, задающая точку в <math>n</math>-мерном пространстве.
 +
 
 +
  <math>R_{k}</math> = [] % Пустое множество
 +
  a = Choose(<math>S_{k}</math>) % Выбор произвольного номера точки, входящей в кластер <math>k</math>
 +
  Add(<math>R_{k}</math>,a) % Добавление точки а во множество представителей
 +
  i = 1 % Текущее количество представителей кластера
 +
  While (i<c) do % Хотим найти с представителей для кластера
 +
  - rmax = 0
 +
  - For ( (y <math>\in</math> <math>S_{k}</math>) and (y <math>\notin</math> <math>P_{k}</math>) ) do % Поиск следующего представителя среди оставшихся точек кластера
 +
  - - rmin = <math>\rho(x^{a}</math>,<math>x^{y})</math>
 +
  - - For ( (j <math>\in</math> <math>R_{k}</math>) and (j <math>\neq</math> a) ) do % Поиск расстояния от точки с номером y до ближайшего представителя
 +
  - - - d = <math>\rho(x^{j}</math>,<math>x^{y})</math> % вычисление расстояния
 +
  - - - If (d < rmin) then
 +
  - - - - rmin = d
 +
  - - - endif
 +
  - - enddo
 +
  - - If (rmin > rmax) % Поиск точки, для которой расстояние до ближайшего представителя является максимальным
 +
  - - - rmax = rmin
 +
  - - - b = y % искомая точка
 +
  - - endif
 +
  - enddo
 +
  - Add(<math>R_{k}</math>,b) % Добавление новой точки в множество представителей
 +
  - i = i + 1 % текущее число представителей
 +
  enddo
 +
  </math>
 +
 +
'''Шаг "Сдвиг представителей к центроиде"'''
 +
 +
Для каждого представителя <math>x^{y}</math> из <math>k</math>-го кластера выполняется сдвиг к его центроиде <math>\mu_{k}</math> в <math>\alpha</math> раз:
 +
 +
<math>\hat{x}^{y} = \alpha\mu_{k} + (1-\alpha)x^{y}</math>.
 +
 +
Получаем множество <math>\hat{R}_{k}</math> из <math>c</math> точек, которые будут далее использоваться как представители этого кластера.
 +
 +
 +
'''Шаг "Присваивание"'''
 +
 +
На данном шаге происходит присвоение неиспользованных точек (строк матрицы <math>x</math>) к кластерам. Для точки-строки <math>p</math> вычисляется расстояние до каждого представителя. Результат: строка <math>p</math> добавляется в поддерево кластера, которому принадлежит наиближайший представитель.
 +
 +
 +
Результатом работы алгоритма является дерево, ветвями которого являются отдельные кластеры. Листьями кластеров являются строки из матрицы <math>x</math>.
  
 
== Вычислительное ядро алгоритма ==
 
== Вычислительное ядро алгоритма ==
  
 +
Вычислительное ядро алгоритма представляет собой итерационное построение <math>k</math> кластеров с помощью иерархического метода, вычисление их центроид <math>\mu_{k}</math> и назначение точек-представителей. В ходе работы вычислительного ядра формируется дерево, в котором точки, выбранные на этапе '''Инициализации''' собраны в <math>h</math> поддеревьев. Точки-представители хранятся в отдельной структуре. Эти точки будут использованы для выбора кластеров для неиспользованных (на этапе '''Инициализации''') точек после работы вычислительного ядра.
  
 
== Макроструктура алгоритма ==
 
== Макроструктура алгоритма ==
 +
 +
Задача алгоритма кластеризации состоит в формировании <math>h</math> кластеров из <math>m</math> точек; число <math>h</math> задано заранее.
 +
 +
На начальном этапе выбирается часть точек, для которых выполняется иерархический алгоритм кластеризации. На начальном этапе каждая точка считается отдельным кластером с центроидой в данной точке. Для каждого кластера считается расстояние для всех остальных. Похожие кластеры объединяются и их точки тоже. На каждом шаге алгоритма происходит вычисление центроиды для новообразованного кластера. Алгоритм выполняется, пока не будет достигнуто необходимое число кластеров.
 +
 +
После этого происходит назначение точек-представителей для каждого кластера и их сдвиг к центроиде.
 +
 +
Далее для неиспользованных точек <math>x</math> происходит вычисление расстояний до всех точек-представителей. Точка помещается в тот кластер, точка-представитель которого находится ближе остальных.
  
 
== Схема реализации последовательного алгоритма ==
 
== Схема реализации последовательного алгоритма ==
 +
 +
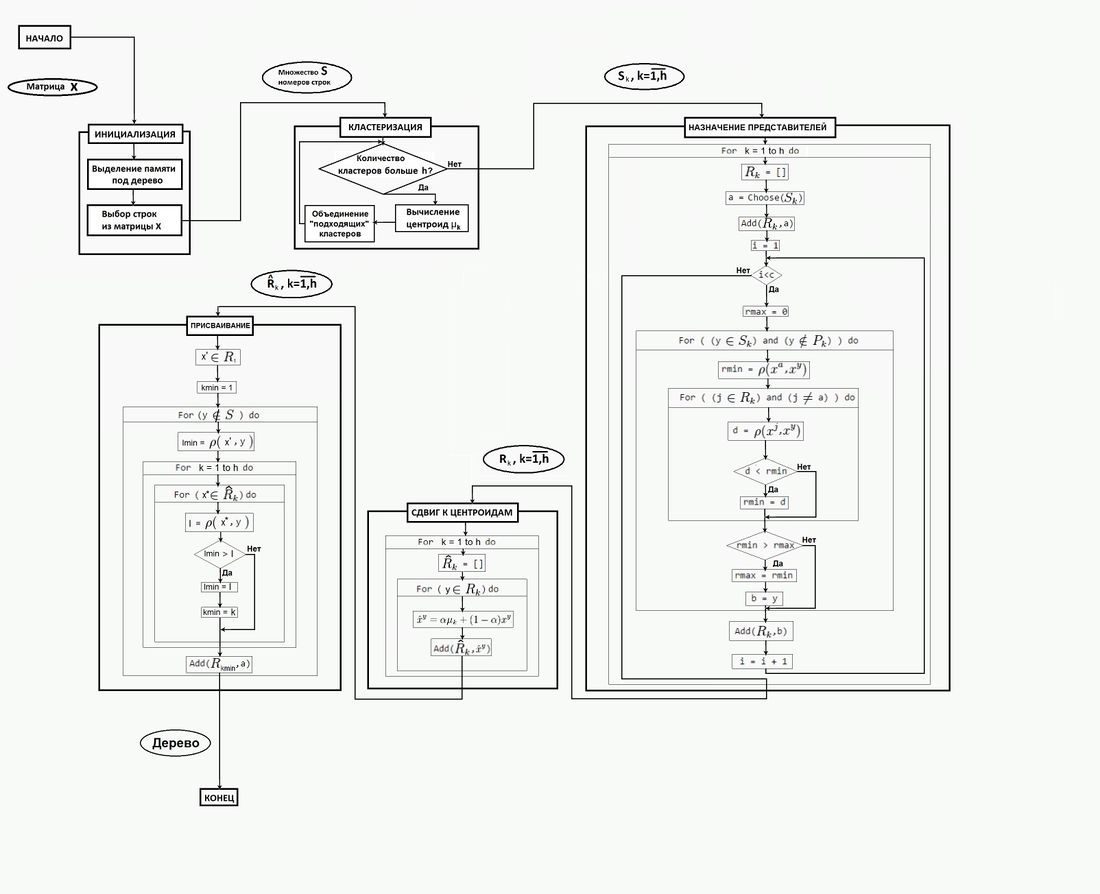
[[Файл:SubCURE4.jpg|1100px|thumb|center|Схема работы алгоритма кластеризации CURE]]
  
 
== Последовательная сложность алгоритма ==
 
== Последовательная сложность алгоритма ==
  
−
Максимальное время выполнения алгоритма <math>O(n^2 logn)</math>. Для двумерного пространства временная сложность может быть <math>O(n^2)</math>. Так что сложность алгоритма не хуже чем у центроидного. То есть при такой размерности входных данных CURE выполняется за полиномиальное время.
+
Входные данные для кластеризации - это <math>n</math> репрезентативных точек в d мерном пространстве и необходимое число <math>h</math> кластеров. Для каждой точки необходимо вычислить расстояние до другой. Сложность этого этапа <math>O(n)</math>. Если искать ближайший кластер простым перебором, то сложность поиска будет <math>O(n)</math> для каждого кластера. Но для эффективного поиска сложность составляет <math>log_2{n}</math>. Эффективный метод описан в статье.<ref>Sudipto Guha (Stanford), Rajeev Rastogi (Bell Labs), Kyuseok Shim (Korea Institute of Technology). CURE: an efficient clustering algorithm for large databases. SIGMOD '98 Proceedings of the 1998 ACM SIGMOD international conference on Management of data, pp 73-84 </ref> Далее каждую точку необходимо вдвинуть к центроиде, сложность этой операции <math>O(2)</math>.
 +
Таким образом худшее время выполнения алгоритма <math>O(n^2 log_2{n})</math>. Для двумерного пространства временная сложность может быть <math>O(n^2)</math>. Так что сложность алгоритма не хуже чем у центроидного. То есть при такой размерности входных данных CURE выполняется за полиномиальное время.<math>~^{[1]}</math>
  
 
== Информационный граф ==
 
== Информационный граф ==
  
 +
'''Шаг "Инициализация"'''
 +
 +
В зависимости от алгоритма случайная выборка номеров строк матрицы <math>x</math> может производится либо зависимо, либо независимо друг от друга.
 +
 +
 +
'''Шаг "Кластеризация"'''
 +
 +
Описанный в разделе иерархический алгоритм кластеризации является последовательным, так как на каждом шаге сравниваются расстояния между центроидами кластеров, некоторые из которых меняются при объединении кластеров.
 +
 +
'''Шаг "Назначение представителей"'''
 +
 +
[[Файл:Points c.png|800px|thumb|center|Последовательный информационный граф для точек-представителей]]
 +
 +
'''Шаг "Сдвиг представителей к центроиде"'''
 +
 +
Данный шаг выполняется независимо для каждой точки-представителя каждого кластера.
 +
 +
 +
'''Шаг "Присваивание"'''
 +
 +
Вычисление расстояний до точек-представителей можно выполнять независимо между собой.
 +
 +
 +
Основные шаги алгоритма информационно зависят от предыдущих шагов.
 +
 +
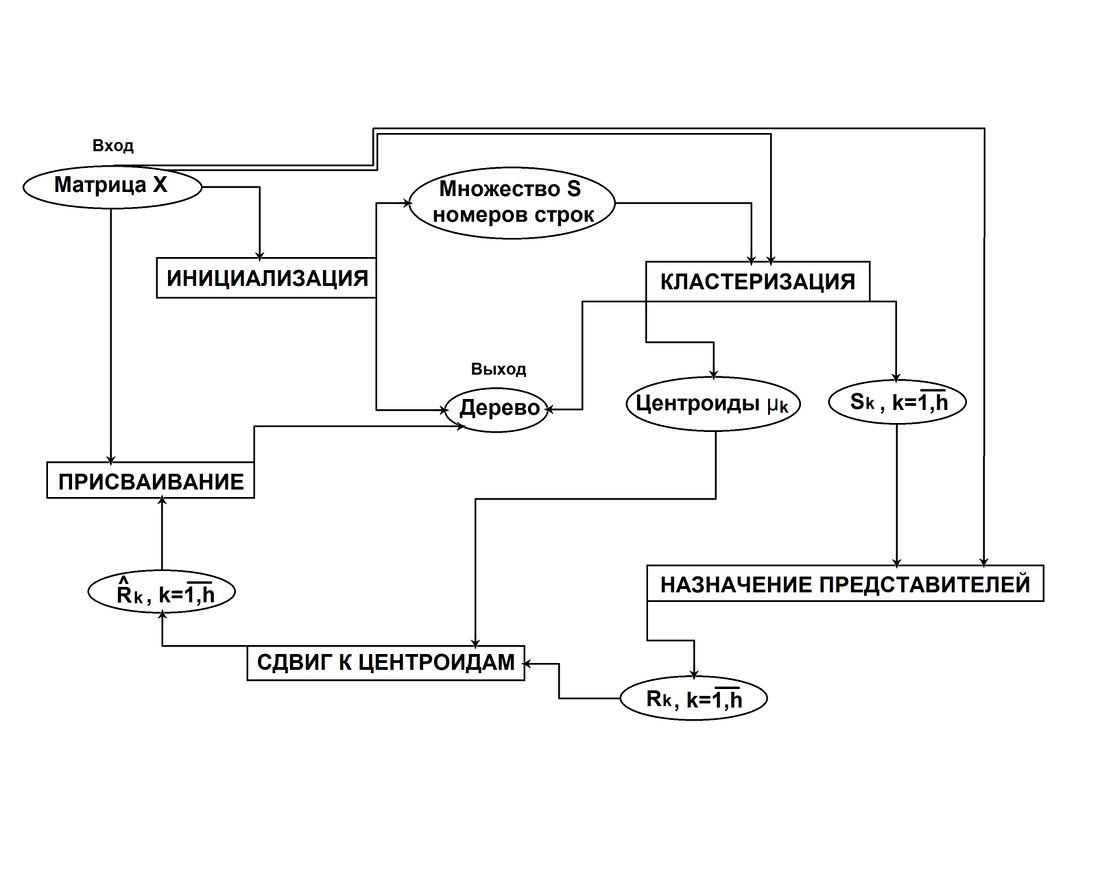
[[Файл:InfoCURE.jpg|1100px|thumb|center|Общий информационный граф алгоритма. В прямоугольниках - шаги алгоритма, в эллипсах - данные.]]
  
 
== Ресурс параллелизма алгоритма ==
 
== Ресурс параллелизма алгоритма ==
 +
 +
'''Шаг "Кластеризация"'''
 +
 +
 +
Шаг 1 (вычисление центроид):
 +
 +
Вычисления центроид для кластеров выполняется независимо, возможно их распараллеливание.
 +
 +
 +
Шаг 2 (поиск "наилучших кластеров для объединения):
 +
 +
На данном этапе вычисляются расстояния между кластерами, что можно сделать независимо друг от друга. Если для определения расстояния между кластерами использовать минимальное расстояние между парами элементов (по одному элементу из каждого кластера), то эти расстояния вычисляются опять же независимо друг от друга, и их можно "распараллелить".
 +
 +
 +
'''Шаг "Назначение представителей"'''
 +
 +
Представители внутри каждого кластера определяются независимо от других кластеров и поддаются распараллеливанию.
 +
 +
 +
'''Шаг "Сдвиг представителей к центроиде"'''
 +
 +
Изменение положения представителей можно сделать независимо как от представителей данного кластера, так и представителей других кластеров. Это также хорошо поддаётся распараллеливанию.
 +
 +
 +
'''Шаг "Присваивание"'''
 +
 +
На данном этапе для каждой точки из таблицы, не использованной на этапе инициализации, выполняется вычисление расстояний до всех точек-представителей. Сравнение расстояний и добавление новых листьев в поддеревья кластеров можно выполнить независимо друг от друга, а значит можно выполнить распараллеливание.
 +
 +
== Входные и выходные данные алгоритма ==
 +
 +
Входные данные: матрица <math>x \in R^{m\times n}</math>, количество кластеров <math>h</math>, число точек представителей <math>c</math>, параметр <math>\alpha</math>, параметр <math>\gamma</math>.
 +
 +
<math>m</math> число точек для кластеризации, <math>n</math> размерность.
 +
 +
Параметр <math>\alpha</math> для сжатия точек представления к центру кластера. В оригинальной статье авторы показывают что <math>\alpha</math> от <math>0.2</math> до <math>0.7</math> помогает хорошо выявлять несферические кластеры и подавлять редкие выбросы.
 +
 +
Параметр <math>\gamma</math> задаёт какая часть от <math>m</math> точек будет использована при случайной выборке точек на шаге "Инициализация". Слишком малое значение <math>\gamma</math> может привести к объединению удалённых кластеров (если ни одна из точек предполагаемого кластера не была выбрана, они были присоединены к другому кластеру на этапе присваивания), а также к разделению кластеров на части (так как конечное количество кластеров фиксировано, а некоторые кластеры могут не набрать достаточное количество мест в выборке, чтобы их кластер сформировался). С другой стороны, скорость вычислений зависит от величины выборки: увеличение выборки при фиксированном числе кластеров <math>h</math> приведёт к дополнительным шагам на этапе кластеризации, а также к дополнительным вычислениям при нахождении кластеров, "наиболее подходящих" для объединения на каждом шаге. Кроме того, увеличение выборки приводит к уменьшению числа оставшихся точек, присвоение которых не входит в [[#Вычислительное ядро алгоритма|Вычислительное ядро алгоритма]].
 +
 +
'''Объём входных данных:''' <math>m\times n + 4</math>
 +
 +
Число точек представителей выбирается в зависимости от данных. Если возможно появление кластеров сложной формы, то точек должно быть больше, чтобы выявить их форму. В оригинальной статье авторы показывают что уже при <math>c</math> равном <math>10</math> достигается неплохая эффективность, в то время как при <math>c = 5</math> большой кластер был разделён на несколько частей.
 +
 +
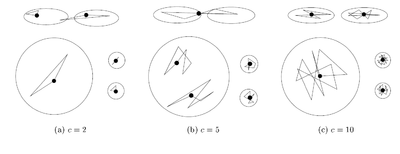
[[Файл:Exampleofalgorithmparameters2.png|400px|thumb|center|Пример работы алгоритма для разных параметров <math>c</math>.]]
 +
 +
 +
Выходные данные:
 +
 +
Дерево, из корня которого выходят поддеревья, содержащие элементы одного кластера; в этих поддеревьях листья обозначают отдельные точки в пространстве.
 +
 +
Состав выходного дерева:
 +
 +
- <math>m</math> листьев (векторов из <math>R^{1 \times n}</math>);
 
   
 
   
 +
- вершины-кластеры представляют собой массивы указателей на листья (число таких указателей равно <math>m</math>);
  
−
== Входные и выходные данные алгоритма ==
+
- корень представляет собой массив указателей на вершины-кластеры (число таких указателей равно числу кластеров <math>h</math>);
 +
 
 +
- также имеется указатель на корень дерева.
  
 +
'''Объём выходных данных:''' <math>m\times n + kp*(m + h + 1)</math>, где <math>kp</math> - коэффициент, равный отношению размера элемента из <math>R</math> к размеру указателя, зависящему от архитектуры платформы.
  
 
== Свойства алгоритма ==
 
== Свойства алгоритма ==
Строка 34: Строка 234:
 
'''Недостатки''': есть необходимость в задании пороговых значений и количества кластеров, работает только на числовых данных, эффективен только для данных низкой размерности
 
'''Недостатки''': есть необходимость в задании пороговых значений и количества кластеров, работает только на числовых данных, эффективен только для данных низкой размерности
  
−
= ЧАСТЬ. Программная реализация алгоритма =
+
= Программная реализация алгоритма =
−
 
 
  
 
== Особенности реализации последовательного алгоритма ==
 
== Особенности реализации последовательного алгоритма ==
−
 
  
 
== Локальность данных и вычислений ==
 
== Локальность данных и вычислений ==
−
 
  
 
== Возможные способы и особенности параллельной реализации алгоритма ==
 
== Возможные способы и особенности параллельной реализации алгоритма ==
−
 
  
 
== Масштабируемость алгоритма и его реализации ==
 
== Масштабируемость алгоритма и его реализации ==
  
−
Данный раздел будет заполнен к 15 ноября.
+
Увы
  
 
== Динамические характеристики и эффективность реализации алгоритма ==
 
== Динамические характеристики и эффективность реализации алгоритма ==
−
 
  
 
== Выводы для классов архитектур ==
 
== Выводы для классов архитектур ==
−
 
  
 
== Существующие реализации алгоритма ==
 
== Существующие реализации алгоритма ==
 
Последовательная реализация CURE-алгоритма для кластеризации для Python/C++ представлена в пакете: [https://github.com/annoviko/pyclustering pyclustering].
 
Последовательная реализация CURE-алгоритма для кластеризации для Python/C++ представлена в пакете: [https://github.com/annoviko/pyclustering pyclustering].
  
−
Также существует параллельная реализация алгоритма, описанная в сборнике [3]. (ДОБАВИТЬ: ЧТО ПРЕДЛАГАЮТ СДЕЛАТЬ АВТОРЫ)
+
Также существует параллельная реализация алгоритма, описанная в сборнике <ref>Panagiotis E. Hadjidoukas, Laurent Amsaleg. OpenMP Shared Memory Parallel Programming.
 +
Volume 4315 of the series Lecture Notes in Computer Science pp 289-299
 +
Parallelization of a Hierarchical Data Clustering Algorithm Using OpenMP</ref>. Алгоритм предложенный в статье использует массив данных состоящий из размеров кластера, его центроида и репрезентативных точек, а при объединении кластеров информацию о новом кластере просто записывают в строчку предыдущего. Также для каждого кластера требуется считать индекс и расстояние до ближайшего кластера. Именно их поиск авторы статьи и предлагают распараллелить.
  
 
= Литература =
 
= Литература =
−
[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
 
  
−
[2] Sudipto Guha, Rajeev Rastogi, Kyuseok Shim. CURE: an efficient clustering algorithm for large databases. SIGMOD '98 Proceedings of the 1998 ACM SIGMOD international conference on Management of data, pp 73-84
+
<references \>
−
 
 
−
[3] Panagiotis E. Hadjidoukas, Laurent Amsaleg. OpenMP Shared Memory Parallel Programming.
 
−
Volume 4315 of the series Lecture Notes in Computer Science pp 289-299
 
−
Parallelization of a Hierarchical Data Clustering Algorithm Using OpenMP
 

Текущая версия на 17:27, 29 ноября 2016

Основные авторы описания:
Ю.А. Антохина, разделы 1.1, 1.5, 1.6, 1.8 - 1.10, 2.7

С.А. Шатков, разделы 1.2 - 1.5, 1.7, 2.4

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Пусть дан набор точек и заданы правила определения расстояния между ними. Задача кластеризации сгруппировать эти точки в определенное число кластеров. Члены одного кластера похожи, а члены разных классов различны.

В алгоритме CURE применяется иерархическая кластеризация. Есть два подхода к иерархической кластеризации. В одном случае один большой кластер на каждом шаге разбивается на несколько, пока число кластеров не будет равно заданному заранее числу кластеров. В другом случае наоборот кластеры, состоящие каждый из одной точки объединяются в большие. Второй метод используется в CURE.

Результат кластеризации зависит от того, как будут представлены кластеры. Например, средним всех точек кластера, или всеми точками кластера. Применение среднего возможно только в евклидовом пространстве. А использование всех точек неустойчиво к случайным выбросам. В CURE используется другой метод: для каждого кластера выбираются точки-представители. Выбирается постоянное число точек, которые будут представлять каждый кластер. Кластеры с наиболее похожими наборами репрезентативных точек объединяются на каждом шаге алгоритма.

За счет использования точек-представителей алгоритм CURE устойчив к выбросам и может выделять кластеры сложной формы и различных размеров.

Описание шагов

Шаг 1. Если все данные использовать сразу как входные для CURE, то эффективность алгоритма будет низкая, а время выполнения большим. Поэтому на первом шаге мы случайным образом выбираем часть точек которые помещаются в память, затем группируем наиболее похожие с помощью иерархического метода в заранее заданное число кластеров. Дальше работаем с кластерами.

Шаг 2. Для каждого кластера выбираем [math]c[/math] точек-представителей, максимально удаленных друг от друга. Чисто [math]c[/math] остается постоянным.

Шаг 3. Объединяем кластеры с наиболее похожими наборами точек-представителей. Если не достигнуто нужное число кластеров, то перейти на шаг 2. Чтобы при объединении кластеров не выбирать каждый раз c точек-представителей из всех точек, мы выбираем их только из [math]2c[/math] точек объединенных кластеров.

Выбранные точки сдвигаются на следующем шаге на [math]\alpha[/math] к центроиду кластера. Алгоритм становится основанным на методе поиска центроида при [math]\alpha = 1[/math], и основанным на всех точках кластера при [math]\alpha = 0[/math].

Пример работы алгоритма для разных параметров [math]\alpha[/math] [1].

1.2 Математическое описание алгоритма

Пусть дана матрица [math]x \in R^{m\times n}[/math], количество кластеров [math]h[/math], число точек-представителей [math]c[/math], параметр [math]\alpha[/math], параметр [math]\gamma[/math]. Каждая строка матрицы представляет собой точку в [math]n[/math] - мерном пространстве.

m число точек для кластеризации, n размерность.

Расстояние [math]\rho(a,b)[/math] между точками [math]a = (a_{1},\dots,a_{n})[/math] и [math]b = (b_{1},\dots,b_{n})[/math] будем вычислять по формуле:

[math]\rho(a,b) = \sqrt{\sum_{i=1}^n (a_{i} - b_{i})^2}[/math]

Шаг "Инициализация"

Выбираются [math]\lceil \gamma m\rceil[/math] строк матрицы случайным образом. Например, можно использовать Алгоритм R.

В основной памяти выделяется куча, часть которой используется для размещения дерева, листьями которого являются выбранные строки, соединённые ребром с вершиной дерева.


Шаг "Кластеризация"

В самом начале шага считаем каждую выбранную точку одноточечным кластером с центроидой в этой же точке.

Далее выполняем следующие шаги 1-2, пока количество кластеров не станет равно [math]h[/math]:

Шаг 1:

Для каждого [math]i[/math]-го кластера вычисляется центроида [math]\mu_{i}[/math] по формуле:

[math]\mu_{i} = \frac{1}{s_{i}}\sum_{j\in S_{i}} x^{j}[/math], где [math]S_{i}[/math] - номера строк матрицы [math]x[/math], входящие в [math]i[/math]-й кластер; [math]s_{i}[/math] - количество элементов в множестве [math]S_{i}[/math]; [math]x^{j}[/math] - [math]j[/math]-я строка матрицы [math]x[/math].

Шаг 2:

Выполняется поиск пары кластеров, "наиболее подходящих" для объединения. В качестве критерия выбора можно рассматривать: наименьшее расстояние между центроидами кластеров или наименьшее расстояние между элементами, входящими в рассматриваемую пару кластеров. Существуют также другие критерии выбора "подходящих" классов, например, сравнение плотности кластеров до объединения и после. Далее выполняется слияние найденных кластеров. Для дерева это означает добавление новой вершины, соединённой ребром с корнем; поддеревья кластеров становятся ветвями этой новой вершины.


Шаг "Назначение представителей"

На данном шаге для каждого кластера определяются [math]c[/math] точек-представителей. Для наилучшего отображения формы множества предполагается использование точек, максимально удалённых друг от друга.

Для этого используем следующий алгоритм:

Пусть [math]i[/math] - текущее количество представителей, [math]S_{k}[/math] - множество номеров строк матрицы [math]x[/math], входящие в [math]k[/math]-й кластер, [math]R_{k}[/math] - множество номеров строк матрицы [math]x[/math], назначенных представителями [math]k[/math]-го кластера, а [math]x^{j}[/math] - вектор-строка матрицы [math]x[/math], задающая точку в [math]n[/math]-мерном пространстве. 

 [math]R_{k}[/math] = [] % Пустое множество
 a = Choose([math]S_{k}[/math]) % Выбор произвольного номера точки, входящей в кластер [math]k[/math]
 Add([math]R_{k}[/math],a) % Добавление точки а во множество представителей
 i = 1 % Текущее количество представителей кластера
 While (i<c) do % Хотим найти с представителей для кластера
 - rmax = 0
 - For ( (y [math]\in[/math] [math]S_{k}[/math]) and (y [math]\notin[/math] [math]P_{k}[/math]) ) do % Поиск следующего представителя среди оставшихся точек кластера
 - - rmin = [math]\rho(x^{a}[/math],[math]x^{y})[/math]
 - - For ( (j [math]\in[/math] [math]R_{k}[/math]) and (j [math]\neq[/math] a) ) do % Поиск расстояния от точки с номером y до ближайшего представителя 
 - - - d = [math]\rho(x^{j}[/math],[math]x^{y})[/math] % вычисление расстояния
 - - - If (d < rmin) then
 - - - - rmin = d
 - - - endif
 - - enddo
 - - If (rmin > rmax) % Поиск точки, для которой расстояние до ближайшего представителя является максимальным
 - - - rmax = rmin
 - - - b = y % искомая точка
 - - endif
 - enddo
 - Add([math]R_{k}[/math],b) % Добавление новой точки в множество представителей
 - i = i + 1 % текущее число представителей
 enddo
 </math>

Шаг "Сдвиг представителей к центроиде"

Для каждого представителя [math]x^{y}[/math] из [math]k[/math]-го кластера выполняется сдвиг к его центроиде [math]\mu_{k}[/math] в [math]\alpha[/math] раз:

[math]\hat{x}^{y} = \alpha\mu_{k} + (1-\alpha)x^{y}[/math].

Получаем множество [math]\hat{R}_{k}[/math] из [math]c[/math] точек, которые будут далее использоваться как представители этого кластера.


Шаг "Присваивание"

На данном шаге происходит присвоение неиспользованных точек (строк матрицы [math]x[/math]) к кластерам. Для точки-строки [math]p[/math] вычисляется расстояние до каждого представителя. Результат: строка [math]p[/math] добавляется в поддерево кластера, которому принадлежит наиближайший представитель.


Результатом работы алгоритма является дерево, ветвями которого являются отдельные кластеры. Листьями кластеров являются строки из матрицы [math]x[/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное построение [math]k[/math] кластеров с помощью иерархического метода, вычисление их центроид [math]\mu_{k}[/math] и назначение точек-представителей. В ходе работы вычислительного ядра формируется дерево, в котором точки, выбранные на этапе Инициализации собраны в [math]h[/math] поддеревьев. Точки-представители хранятся в отдельной структуре. Эти точки будут использованы для выбора кластеров для неиспользованных (на этапе Инициализации) точек после работы вычислительного ядра.

1.4 Макроструктура алгоритма

Задача алгоритма кластеризации состоит в формировании [math]h[/math] кластеров из [math]m[/math] точек; число [math]h[/math] задано заранее.

На начальном этапе выбирается часть точек, для которых выполняется иерархический алгоритм кластеризации. На начальном этапе каждая точка считается отдельным кластером с центроидой в данной точке. Для каждого кластера считается расстояние для всех остальных. Похожие кластеры объединяются и их точки тоже. На каждом шаге алгоритма происходит вычисление центроиды для новообразованного кластера. Алгоритм выполняется, пока не будет достигнуто необходимое число кластеров.

После этого происходит назначение точек-представителей для каждого кластера и их сдвиг к центроиде.

Далее для неиспользованных точек [math]x[/math] происходит вычисление расстояний до всех точек-представителей. Точка помещается в тот кластер, точка-представитель которого находится ближе остальных.

1.5 Схема реализации последовательного алгоритма

Схема работы алгоритма кластеризации CURE

1.6 Последовательная сложность алгоритма

Входные данные для кластеризации - это [math]n[/math] репрезентативных точек в d мерном пространстве и необходимое число [math]h[/math] кластеров. Для каждой точки необходимо вычислить расстояние до другой. Сложность этого этапа [math]O(n)[/math]. Если искать ближайший кластер простым перебором, то сложность поиска будет [math]O(n)[/math] для каждого кластера. Но для эффективного поиска сложность составляет [math]log_2{n}[/math]. Эффективный метод описан в статье.[1] Далее каждую точку необходимо вдвинуть к центроиде, сложность этой операции [math]O(2)[/math]. Таким образом худшее время выполнения алгоритма [math]O(n^2 log_2{n})[/math]. Для двумерного пространства временная сложность может быть [math]O(n^2)[/math]. Так что сложность алгоритма не хуже чем у центроидного. То есть при такой размерности входных данных CURE выполняется за полиномиальное время.[math]~^{[1]}[/math]

1.7 Информационный граф

Шаг "Инициализация"

В зависимости от алгоритма случайная выборка номеров строк матрицы [math]x[/math] может производится либо зависимо, либо независимо друг от друга.


Шаг "Кластеризация"

Описанный в разделе иерархический алгоритм кластеризации является последовательным, так как на каждом шаге сравниваются расстояния между центроидами кластеров, некоторые из которых меняются при объединении кластеров.

Шаг "Назначение представителей"

Последовательный информационный граф для точек-представителей

Шаг "Сдвиг представителей к центроиде"

Данный шаг выполняется независимо для каждой точки-представителя каждого кластера.


Шаг "Присваивание"

Вычисление расстояний до точек-представителей можно выполнять независимо между собой.


Основные шаги алгоритма информационно зависят от предыдущих шагов.

Общий информационный граф алгоритма. В прямоугольниках - шаги алгоритма, в эллипсах - данные.

1.8 Ресурс параллелизма алгоритма

Шаг "Кластеризация"


Шаг 1 (вычисление центроид):

Вычисления центроид для кластеров выполняется независимо, возможно их распараллеливание.


Шаг 2 (поиск "наилучших кластеров для объединения):

На данном этапе вычисляются расстояния между кластерами, что можно сделать независимо друг от друга. Если для определения расстояния между кластерами использовать минимальное расстояние между парами элементов (по одному элементу из каждого кластера), то эти расстояния вычисляются опять же независимо друг от друга, и их можно "распараллелить".


Шаг "Назначение представителей"

Представители внутри каждого кластера определяются независимо от других кластеров и поддаются распараллеливанию.


Шаг "Сдвиг представителей к центроиде"

Изменение положения представителей можно сделать независимо как от представителей данного кластера, так и представителей других кластеров. Это также хорошо поддаётся распараллеливанию.


Шаг "Присваивание"

На данном этапе для каждой точки из таблицы, не использованной на этапе инициализации, выполняется вычисление расстояний до всех точек-представителей. Сравнение расстояний и добавление новых листьев в поддеревья кластеров можно выполнить независимо друг от друга, а значит можно выполнить распараллеливание.

1.9 Входные и выходные данные алгоритма

Входные данные: матрица [math]x \in R^{m\times n}[/math], количество кластеров [math]h[/math], число точек представителей [math]c[/math], параметр [math]\alpha[/math], параметр [math]\gamma[/math].

[math]m[/math] число точек для кластеризации, [math]n[/math] размерность.

Параметр [math]\alpha[/math] для сжатия точек представления к центру кластера. В оригинальной статье авторы показывают что [math]\alpha[/math] от [math]0.2[/math] до [math]0.7[/math] помогает хорошо выявлять несферические кластеры и подавлять редкие выбросы.

Параметр [math]\gamma[/math] задаёт какая часть от [math]m[/math] точек будет использована при случайной выборке точек на шаге "Инициализация". Слишком малое значение [math]\gamma[/math] может привести к объединению удалённых кластеров (если ни одна из точек предполагаемого кластера не была выбрана, они были присоединены к другому кластеру на этапе присваивания), а также к разделению кластеров на части (так как конечное количество кластеров фиксировано, а некоторые кластеры могут не набрать достаточное количество мест в выборке, чтобы их кластер сформировался). С другой стороны, скорость вычислений зависит от величины выборки: увеличение выборки при фиксированном числе кластеров [math]h[/math] приведёт к дополнительным шагам на этапе кластеризации, а также к дополнительным вычислениям при нахождении кластеров, "наиболее подходящих" для объединения на каждом шаге. Кроме того, увеличение выборки приводит к уменьшению числа оставшихся точек, присвоение которых не входит в Вычислительное ядро алгоритма.

Объём входных данных: [math]m\times n + 4[/math]

Число точек представителей выбирается в зависимости от данных. Если возможно появление кластеров сложной формы, то точек должно быть больше, чтобы выявить их форму. В оригинальной статье авторы показывают что уже при [math]c[/math] равном [math]10[/math] достигается неплохая эффективность, в то время как при [math]c = 5[/math] большой кластер был разделён на несколько частей.

Пример работы алгоритма для разных параметров [math]c[/math].


Выходные данные:

Дерево, из корня которого выходят поддеревья, содержащие элементы одного кластера; в этих поддеревьях листья обозначают отдельные точки в пространстве.

Состав выходного дерева:

- [math]m[/math] листьев (векторов из [math]R^{1 \times n}[/math]);

- вершины-кластеры представляют собой массивы указателей на листья (число таких указателей равно [math]m[/math]);

- корень представляет собой массив указателей на вершины-кластеры (число таких указателей равно числу кластеров [math]h[/math]);

- также имеется указатель на корень дерева.

Объём выходных данных: [math]m\times n + kp*(m + h + 1)[/math], где [math]kp[/math] - коэффициент, равный отношению размера элемента из [math]R[/math] к размеру указателя, зависящему от архитектуры платформы.

1.10 Свойства алгоритма

Алгоритм CURE выполняет иерархическую кластеризацию с использованием набора определяющих точек. Он действует только в евклидовом пространстве и предназначен для кластеризации очень больших наборов числовых данных.

Преимущества: выполняет кластеризацию на высоком уровне даже при наличии выбросов, выделяет кластеры сложной формы и различных размеров, обладает линейно зависимыми требованиями к месту хранения данных и квадратичную временную сложность для данных высокой размерности.

Недостатки: есть необходимость в задании пороговых значений и количества кластеров, работает только на числовых данных, эффективен только для данных низкой размерности

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Увы

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Последовательная реализация CURE-алгоритма для кластеризации для Python/C++ представлена в пакете: pyclustering.

Также существует параллельная реализация алгоритма, описанная в сборнике [2]. Алгоритм предложенный в статье использует массив данных состоящий из размеров кластера, его центроида и репрезентативных точек, а при объединении кластеров информацию о новом кластере просто записывают в строчку предыдущего. Также для каждого кластера требуется считать индекс и расстояние до ближайшего кластера. Именно их поиск авторы статьи и предлагают распараллелить.

3 Литература

<references \>

  1. ↑ Sudipto Guha (Stanford), Rajeev Rastogi (Bell Labs), Kyuseok Shim (Korea Institute of Technology). CURE: an efficient clustering algorithm for large databases. SIGMOD '98 Proceedings of the 1998 ACM SIGMOD international conference on Management of data, pp 73-84
  2. ↑ Panagiotis E. Hadjidoukas, Laurent Amsaleg. OpenMP Shared Memory Parallel Programming. Volume 4315 of the series Lecture Notes in Computer Science pp 289-299 Parallelization of a Hierarchical Data Clustering Algorithm Using OpenMP
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:JuliaA/Алгоритм_кластеризации_с_использованием_представлений&oldid=19479