Участник:DenisAnuprienko/Метод Штрассена: различия между версиями
| (не показано 11 промежуточных версий этого же участника) | |||
| Строка 77: | Строка 77: | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| − | Метод | + | Метод Штрассена позволяет сократить число умножений, поэтому оценивается именно оно. В методе Штрассена число умножений составляет <math>O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})</math>. |
== Информационный граф == | == Информационный граф == | ||
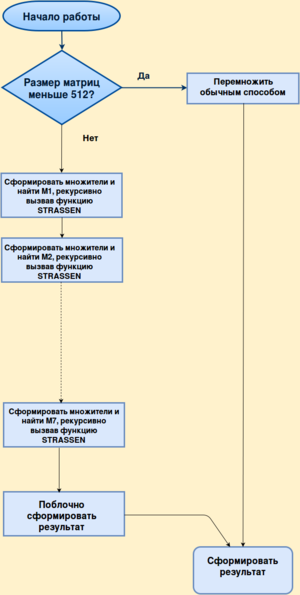
| − | Рассмотрим блок-схему для последовательной реализации рекурсивной функции Strassen | + | Рассмотрим блок-схему для последовательной реализации рекурсивной функции Strassen для числа <math>N_{min}</math>, равного 512. |
[[Файл:Serial.png|300px|center]] | [[Файл:Serial.png|300px|center]] | ||
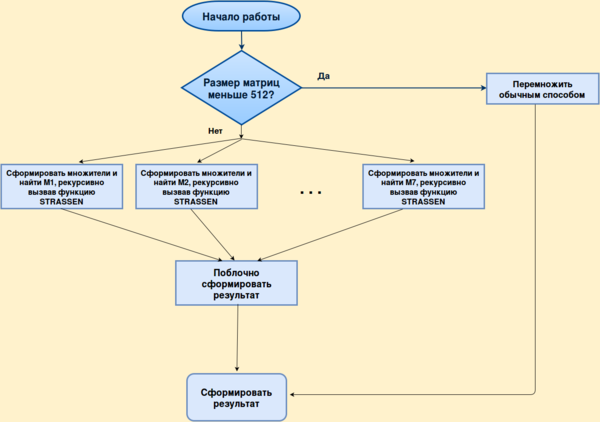
Здесь 7 рекурсивных вызовов функции Strassen можно выполнять параллельно: | Здесь 7 рекурсивных вызовов функции Strassen можно выполнять параллельно: | ||
| − | [[Файл: | + | [[Файл:Parallel_1.png|600px|center]] |
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| − | Умножения, которые необходимы для нахождения матриц <math>M_1, ..., M_7</math>, можно провести параллельно. Их можно предоставить 7 процессам (1 хозяин, который раздает задания 6 рабочим и получает результаты, а также работает вместе с | + | Умножения, которые необходимы для нахождения матриц <math>M_1, ..., M_7</math>, можно провести параллельно. Их можно предоставить 7 процессам (1 хозяин, который раздает задания 6 рабочим и получает результаты, а также работает вместе с рабочими) или 8 процессам (1 хозяин, который раздает задания 7 рабочим и получает результаты). |
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| − | Нет никаких предположений насчет структуры матриц. | + | Нет никаких предположений насчет структуры матриц. Считается, что это обычные плотные матрицы. Они хранятся в виде одномерного массива, что позволяет легко выделять из них подматрицы. |
== Свойства алгоритма == | == Свойства алгоритма == | ||
| Строка 104: | Строка 104: | ||
== Особенности реализации последовательного алгоритма == | == Особенности реализации последовательного алгоритма == | ||
| + | Матрицы хранятся как одномерные массивы. Благодаря этому в составе матрицы легко выделить подматрицу, зная размеры подматрицы и родительской матрицы, а также указатель на начало подматрицы.<br> | ||
| + | В этом состоит выгодное отличие от некоторых существующих реализаций, где при использовании подматриц выделяется отдельная память. | ||
== Локальность данных и вычислений == | == Локальность данных и вычислений == | ||
| Строка 117: | Строка 119: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| − | По описанным в предыдущем пункте причинам предлагаемая реализация с распараллеливанием 1 уровня рекурсии может быть запущена только на определенном количестве | + | По описанным в предыдущем пункте причинам предлагаемая реализация с распараллеливанием 1 уровня рекурсии может быть запущена только на определенном количестве процессов. Запуск на другом количестве процессов означает использование уже другой программы, поэтому оценить масшатбируемость в текущей реализации не представляется возможным. |
| + | |||
| + | === Сравнение работы последовательной и параллельной реализаций === | ||
| + | Эксперименты проводились на суперкомпьютере [http://users.parallel.ru/wiki/pages/22-config "Ломоносов"]. Использовались gcc и mpicc 4.4.7 с флагом компиляции -O3, а также OpenMPI 1.8.4. Параллельная версия задействовала 8 процессов. | ||
| + | {| class="wikitable" | ||
| + | |+Результаты запусков на "Ломоносове" | ||
| + | |- | ||
| + | |Размер матрицы | ||
| + | |Последовательная реализация | ||
| + | |Параллельная реализация с использованием MPI | ||
| + | |Ускорение | ||
| + | |- | ||
| + | |512 | ||
| + | |0.18 c | ||
| + | |0.035 c | ||
| + | |5.14 | ||
| + | |- | ||
| + | |1024 | ||
| + | |1.99 c | ||
| + | |0.40 c | ||
| + | |4.98 | ||
| + | |- | ||
| + | |2048 | ||
| + | |16.1 c | ||
| + | |3.45 c | ||
| + | |4.67 | ||
| + | |- | ||
| + | |4096 | ||
| + | |230.1 c | ||
| + | |71.0 c | ||
| + | |3.23 | ||
| + | |- | ||
| + | |} | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
Текущая версия на 12:44, 10 декабря 2016
Основные авторы описания: Д.В.Ануприенко.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Исходный код
- 2.2 Особенности реализации последовательного алгоритма
- 2.3 Локальность данных и вычислений
- 2.4 Возможные способы и особенности параллельной реализации алгоритма
- 2.5 Масштабируемость алгоритма и его реализации
- 2.6 Динамические характеристики и эффективность реализации алгоритма
- 2.7 Выводы для классов архитектур
- 2.8 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Штрассена предназначен для умножения матриц. Здесь будет рассмотрен вариант метода, который можно применять к квадратным матрицам размера [math]N = 2^n[/math]. В таком случае две матрицы можно умножить быстрее, чем за [math]O(N^3)[/math].
1.2 Математическое описание алгоритма
Пусть имеются две матрицы [math]A, B \in \mathbb{R}^{N\times N}[/math]. Представим их в блочном виде:
[math]
A =
\begin{bmatrix}
A_{11} & A_{12}\\
A_{21} & A_{22}\\
\end{bmatrix},
B =
\begin{bmatrix}
B_{11} & B_{12}\\
B_{21} & B_{22}\\
\end{bmatrix}.
[/math]
При обычном умножении матриц пришлось бы совершить 8 умножений подматриц порядка [math]N/2[/math]. В методе Штрассена предлагается обойтись всего 7 умножениями. Находятся 7 вспомогательных подматриц [math]M_1, ..., M_7[/math] по следующим формулам:
[math]
M_1 = (A_{11} + A_{22})(B_{11} + B_{22})
[/math]
[math]
M_2 = (A_{21} + A_{22})B_{11}
[/math]
[math]
M_3 = A_{11}(B_{12} - B_{22})
[/math]
[math]
M_4 = A_{22}(B_{21} - B_{11})
[/math]
[math]
M_5 = (A_{11} + A_{12})B_{22}
[/math]
[math]
M_6 = (A_{21} - A_{22})(B_{11} + B_{12})
[/math]
[math]
M_7 = (A_{12} - A_{22})(B_{21} + B_{22})
[/math]
После этого матрица [math]C[/math], являющаяся произведением [math]A[/math] и [math]B[/math], находится по формулам
[math]
C_{11} = M_1 + M_4 - M_5 + M_7
[/math]
[math]
C_{12} = M_3 + M_5
[/math]
[math]
C_{21} = M_2 + M_4
[/math]
[math]
C_{22} = M_1 - M_2 + M_3 + M_6
[/math]
Если и умножения подматриц, необходимые для нахождения [math]M_i[/math], проводить по такой же схеме, получается рекурсивный алгоритм. Всего в нем понадобится выполнить [math]O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})[/math] умножений. На практике рекурсию можно не разворачивать до конца, а использовать обычное умножение уже на матрицах размера 512.
[math][/math]
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на формирование множителей для умножения подматриц, рекурсивные вызовы и умножение матриц обычным методом в конце рекурсии.
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
- Если размер матриц меньше некоторого числа [math]N_{min}[/math], умножить их обычным способом.
- Иначе
- Сформировать множители для матрицы [math]M_1[/math]
- Применить метод Штрассена для этих множителей
- Сформировать множители для матрицы [math]M_2[/math]
- Применить метод Штрассена для этих множителей
- ...
- Сформировать множители для матрицы [math]M_7[/math]
- Применить метод Штрассена для этих множителей
- Сформировать результат из матриц [math]M_1, ..., M_7[/math].
1.6 Последовательная сложность алгоритма
Метод Штрассена позволяет сократить число умножений, поэтому оценивается именно оно. В методе Штрассена число умножений составляет [math]O(7^{log_2N}) = O(N^{log_27}) \approx O(N^{2.81})[/math].
1.7 Информационный граф
Рассмотрим блок-схему для последовательной реализации рекурсивной функции Strassen для числа [math]N_{min}[/math], равного 512.
Здесь 7 рекурсивных вызовов функции Strassen можно выполнять параллельно:
1.8 Ресурс параллелизма алгоритма
Умножения, которые необходимы для нахождения матриц [math]M_1, ..., M_7[/math], можно провести параллельно. Их можно предоставить 7 процессам (1 хозяин, который раздает задания 6 рабочим и получает результаты, а также работает вместе с рабочими) или 8 процессам (1 хозяин, который раздает задания 7 рабочим и получает результаты).
1.9 Входные и выходные данные алгоритма
Нет никаких предположений насчет структуры матриц. Считается, что это обычные плотные матрицы. Они хранятся в виде одномерного массива, что позволяет легко выделять из них подматрицы.
1.10 Свойства алгоритма
- Алгоритм устойчив
- Алгоритм детерминирован
2 Программная реализация алгоритма
2.1 Исходный код
2.2 Особенности реализации последовательного алгоритма
Матрицы хранятся как одномерные массивы. Благодаря этому в составе матрицы легко выделить подматрицу, зная размеры подматрицы и родительской матрицы, а также указатель на начало подматрицы.
В этом состоит выгодное отличие от некоторых существующих реализаций, где при использовании подматриц выделяется отдельная память.
2.3 Локальность данных и вычислений
Все действия с двумя главными матрицами проводит только процесс-хозяин. Каждый процесс также создает и освобождает для себя вспомогательные матрицы [math]M_i[/math], а также две матрицы для записи множителей для нахождения [math]M_i[/math].
2.4 Возможные способы и особенности параллельной реализации алгоритма
Устройство метода Штрассена накладывает ограничения на количество процессов для распараллеливания.
- Как уже было отмечено, распараллеливать можно 7 умножений, из которых получаются матрицы [math]M_1, ..., M_7[/math], с помощью 7 или 8 процессов.
- Распараллеливание этих 7 умножений с помощью меньшего, чем 7, или большего, чем 8, числа процессов не рассматривается, так как в первом случае количество пересылок будет тем же, а время работы - большим, а во втором случае получается более 1 процесса на 1 умножение, что является дополнительным усложнением с негарантированной пользой.
- В таком случае, распараллеливание [math]n[/math] уровней рекурсии требует как минимум [math]7^n[/math] процессов. Количество процессов меняется тогда и только тогда, когда меняется число распараллеливаемых уровней рекурсии.
- Здесь будет рассмотрен вариант метода Штрассена, где распараллеливается 1 уровень рекурсии с помощью 8 процессов: 1 хозяина и 7 рабочих. Эта версия работает несколько быстрее, чем версия с 7 процессами.
2.5 Масштабируемость алгоритма и его реализации
По описанным в предыдущем пункте причинам предлагаемая реализация с распараллеливанием 1 уровня рекурсии может быть запущена только на определенном количестве процессов. Запуск на другом количестве процессов означает использование уже другой программы, поэтому оценить масшатбируемость в текущей реализации не представляется возможным.
2.5.1 Сравнение работы последовательной и параллельной реализаций
Эксперименты проводились на суперкомпьютере "Ломоносов". Использовались gcc и mpicc 4.4.7 с флагом компиляции -O3, а также OpenMPI 1.8.4. Параллельная версия задействовала 8 процессов.
| Размер матрицы | Последовательная реализация | Параллельная реализация с использованием MPI | Ускорение |
| 512 | 0.18 c | 0.035 c | 5.14 |
| 1024 | 1.99 c | 0.40 c | 4.98 |
| 2048 | 16.1 c | 3.45 c | 4.67 |
| 4096 | 230.1 c | 71.0 c | 3.23 |