Участник:Tereshinvs/MST Clusterization: различия между версиями
| (не показано 46 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | |||
== Структура и свойства алгоритма == | == Структура и свойства алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Кластеризация | + | Кластеризация — это задача статистического анализа, состоящая в разбиении множества объектов на группы, называемые кластерами, внутри которых объекты обладают похожими свойствами (чаще всего, это означает близость относительно заданной метрики). Изначально группы неизвестны, в зависимости от постановки задачи может быть также известно или неизвестно общее число кластеров. |
| − | |||
| − | |||
Постановка задачи также может различаться характером входных данных: | Постановка задачи также может различаться характером входных данных: | ||
| − | # Набор признаков <math> \left\{ v_1, v_2, \ldots, v_N \right\} </math> в некотором метрическом пространстве с метрикой <math> \rho(x, y) </math> | + | # Набор признаков <math> V = \left\{ v_1, v_2, \ldots, v_N \right\} </math> в некотором метрическом пространстве с метрикой <math> \rho(x, y) </math> |
# Матрица отношений между объектами: симметричная матрица вещественных чисел размером <math> N \times N </math> с неотрицательными элементами с нулевой диагональю. | # Матрица отношений между объектами: симметричная матрица вещественных чисел размером <math> N \times N </math> с неотрицательными элементами с нулевой диагональю. | ||
| − | + | В данной статье рассматривается постановка с известным количеством кластеров <math> K </math>. | |
| + | |||
| + | В данной статье рассматривается алгоритм алгоритм кластеризации на основе MST (Minimum spanning tree — минимальное остовное дерево). | ||
| + | |||
| + | Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер. | ||
| + | |||
| + | Общая схема алгоритма: | ||
| + | # Построение минимального остовного дерева одним из известных методов (алгоритмы Крускала, Прима, Борувки и их комбинации; наиболее пригодным для параллельного исполнения считается алгоритм Борувки) | ||
| + | # Удаление <math> K-1 </math> самых длинных рёбер из минимального остовного дерева. | ||
| + | |||
| + | В данной статье рассматривается версия алгоритма с использованием алгоритма Борувки. | ||
| + | |||
| + | В случае постановки задачи в виде набора признаков в подходящем метрическом пространстве возможна также предварительная подготовка графа, состоящая из построения триангуляции Делоне. Так как любое минимальное остовное дерево в этом случае принадлежит триангуляции Делоне, в некоторых случаях это позволяет значительно улучшить ассимптотику алгоритма. Данная часть алгоритма не является обязательной, поэтому подробно рассматриваться не будет. | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| + | Пусть <math>V</math> — множество объектов, <math>Y</math> — множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами <math>\rho(x,y)</math>. Требуется разбить выборку на непересекающиеся подмножества, называемые ''кластерами'', так, чтобы каждый кластер состоял из объектов, близких по метрике <math>\rho</math>, а объекты разных кластеров существенно отличались. При этом каждому объекту <math>v_i\in V</math> | ||
| + | приписывается номер кластера <math>y_i</math>. | ||
| + | |||
| + | ''Алгоритм кластеризации'' — это функция <math>a\colon V\to Y</math>, которая любому объекту <math>v\in V</math> ставит в соответствие номер кластера <math>y\in Y</math>. Множество <math>Y</math> в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного ''критерия качества'' кластеризации. | ||
| + | |||
| + | В данном случае задачу можно сформулировать так: выбрать пороговое значение веса ребра <math>W</math>, так чтобы объекты, соединённые ребром весом меньше <math>W</math> лежали в одном кластере, а соединённые ребром весом больше <math>W</math> — в разных. | ||
| + | |||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| + | Вычислительным ядром алгоритма является построение минимального остовного дерева для графа отношений с помощью алгоритма Борувки. В некоторых случаях построение минимального остовного дерева имеет ту же сложность, что и предварительное построение триангуляции Делоне, если оно используется. | ||
| + | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| + | Основной алгоритм можно разделить на следующие части: | ||
| + | # Нахождение для каждой вершины наименьшего ребра, инциндентного ней | ||
| + | # Добавление найденных наименьших вершин в MST | ||
| + | # "Склейка" компонент связности MST | ||
| + | # Нахождение веса <math>W_{K-1}</math> <math>(K-1)</math>-ого наибольшего ребра | ||
| + | # Удаление рёбер весом не меньше чем <math>W_{K-1}</math>. | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| + | <source lang="text" line start="0" highlight="1,9"> | ||
| + | Ввод: граф V | ||
| + | |||
| + | Поместить каждую вершину в отдельное дерево леса T | ||
| + | Пока в T больше одной компоненты связности: | ||
| + | Для каждой компоненты C из T: | ||
| + | S — пустое множество рёбер | ||
| + | Для каждой вершины v в C: | ||
| + | Найти кратчайшее ребро с одним концом v, а другим не из C, и поместить его в S | ||
| + | Добавить кратчайшее ребро из S в T | ||
| + | Объединить компоненты связности | ||
| + | T — MST | ||
| + | |||
| + | Найти W — вес (K-1)-ого максимального ребра в T | ||
| + | Удалить из T рёбра с весом большим или равным W | ||
| + | |||
| + | Пронумеровать компоненты связности | ||
| + | |||
| + | Вывод: номера компонент связности для каждой вершины | ||
| + | </source> | ||
| + | |||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | <!--# Для приближённого построения триангуляции Делонэ существуют алгоритмы разделяй-и-властвуй, имеющие гарантированную сложность <math>O(N \log N)</math>. Кроме того, если имеется некоторая априорная информация о рассматриваемых объектах, в некоторых случаях имеются алгоритмы со средней сложностью <math>O(N)</math>;--> | ||
| + | # Нахождение ребер наименьшего веса для всех компонент связности требует <math>O(V)</math> операций на каждом шаге, где <math>V</math> — число рёбер в графе. | ||
| + | # Добавление новых рёбер в MST требует <math>O(N)</math> операций за всё время работы алгоритма. | ||
| + | # При использовании структуры данных система непересекающихся множеств с ранговой эвристикой, объединение деревьев требует примерно , где <math>O(N)</math> операций. | ||
| + | # Доказано, что количество шагов алгоритма <math>O(\log N)</math>. | ||
| + | |||
| + | Итого <math>O(V \log N)</math> операций. При использовании триангуляции Делонэ в некоторых случаях <math>V</math> имеет тот же порядок, что и <math>N</math>, поэтому общая сложность <math>O(N \log N)</math>. В общем же случае сложность составляет <math>O(N^2 \log N)</math> | ||
| + | |||
| + | Удаление <math>K-1</math> рёбер можно осуществить за <math>O(N)</math> операций. | ||
| + | |||
| + | Итак, общая сложность алгоритма в общем случае <math>O(N^2 \log N)</math>. | ||
| + | |||
=== Информационный граф === | === Информационный граф === | ||
| + | [[File:Tereshinvs_mst_scheme.png|frame|center|alt=Информационный граф|Информационный граф алгоритма кластеризации на основе минимального остовного дерева]] | ||
| + | |||
| + | Изначально все вершины находятся в своих собственных деревьях (стадия вершин). Затем с помощью нахождения кратчайших рёбер, соединяющих разные поддеревья, происходит слияние поддеревьев (стадия объединения деревьев) до тех пор, пока не останется одно дерево, являющееся минимальным остовным деревом исходного графа. После этого нужно будет лишь удалить нужное количество рёбер (выделение кластеров). | ||
| + | |||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | Основным местом для распараллеливания алгоритма является поиск наименьшего ребра из одной компоненты связности в другие. Так как компоненты связности в данном случае независимы, то отдельные узлы вычислительной системы могут выполнять поиск наименьших рёбер независимо. | ||
| + | |||
| + | Узким местом является нахождение k-ой порядковой статистики для выделения кластеров, а так же объединение компонент связности. Но всего объединений компонент связности <math>N-1</math>, поэтому при его реализации с помощью структуры данных система непересекабщихся множеств с ранговой эвристикой общая сложность за всё время работы алгоритма будет близко к <math>O(N)</math>. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
Входными данными являются число <math> N </math> (количество элементов рассматриваемого множества) и матрица вещественных чисел размера <math> N \times N </math> отношений между элементами этого множества. Матрица предполагается симметричной, а её диагональные элементы равными нулю, поэтому её размер можно оценить как <math> \tfrac{N(N-1)}{2} </math>. | Входными данными являются число <math> N </math> (количество элементов рассматриваемого множества) и матрица вещественных чисел размера <math> N \times N </math> отношений между элементами этого множества. Матрица предполагается симметричной, а её диагональные элементы равными нулю, поэтому её размер можно оценить как <math> \tfrac{N(N-1)}{2} </math>. | ||
| − | Кроме того, имеется натуральное число <math> K \leqslant N </math> | + | Кроме того, имеется натуральное число <math> K \leqslant N </math> — требуемое количество кластеров. |
| − | Выходными данными являются <math> N </math> натуральных чисел от <math> 1 </math> до <math> K </math> | + | Выходными данными являются <math> N </math> натуральных чисел от <math> 1 </math> до <math> K </math> — номера кластеров, в которые определена каждая вершина. При этом, каждый кластер содержит хотя бы одну вершину. |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| + | Отрицательной сторой алгоритмов кластеризации, основанных на минимальных остовных деревьях, является их чувствительность к выбросам. С другой стороны, эти алгоритмы способны выделять кластеры произвольной формы, а результат их применения интуитивно понятен. | ||
| + | |||
| + | == Программная реализация алгоритма == | ||
| − | == | + | === Особенности реализации последовательного алгоритма === |
| + | |||
| + | === Локальность данных и вычислений === | ||
| + | |||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | |||
| + | Интересной особенностью использования библиотеки Boost::graph::distributed является возможность задания изначального распределения вершин графа по процессам. К сложностям использования можно отнести нечитаемые сообщения об ошибках инстанцирования шаблонов С++ и отсутствие большого числа примеров использования библиотеки в интернете. | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | В этом параграфе описывается масштабируемость параллельной реализации алгоритма из библиотеки Boost::graph::distributed. | ||
| + | |||
| + | С использованием библиотеки Boost::graph::distributed программу можно реализовать следующим образом (указана только часть построения MST): | ||
| + | |||
| + | <source lang="C++" line start="0" highlight="1,9"> | ||
| + | #include <boost/graph/use_mpi.hpp> | ||
| + | #include <boost/graph/distributed/mpi_process_group.hpp> | ||
| + | #include <boost/graph/distributed/adjacency_list.hpp> | ||
| + | #include <boost/graph/distributed/dehne_gotz_min_spanning_tree.hpp> | ||
| + | #include <boost/graph/distributed/vertex_list_adaptor.hpp> | ||
| + | #include <boost/graph/metis.hpp> | ||
| + | |||
| + | #include <iostream> | ||
| + | #include <fstream> | ||
| + | #include <vector> | ||
| + | |||
| + | typedef boost::adjacency_list< | ||
| + | boost::listS, | ||
| + | boost::distributedS< | ||
| + | boost::graph::distributed::mpi_process_group, | ||
| + | boost::vecS | ||
| + | >, | ||
| + | boost::undirectedS, | ||
| + | boost::no_property, | ||
| + | boost::property< | ||
| + | boost::edge_weight_t, | ||
| + | float | ||
| + | > | ||
| + | > Graph; | ||
| + | |||
| + | typedef boost::graph_traits<Graph>::edge_descriptor Edge; | ||
| + | |||
| + | int main(int argc, char* argv[]) | ||
| + | { | ||
| + | boost::mpi::environment env(argc, argv); | ||
| + | |||
| + | std::ifstream in("big.graph"); | ||
| + | boost::graph::metis_reader reader(in); | ||
| + | |||
| + | Graph graph( | ||
| + | reader.begin(), reader.end(), | ||
| + | reader.weight_begin(), | ||
| + | reader.num_vertices() | ||
| + | ); | ||
| + | |||
| + | typedef boost::property_map<Graph, boost::edge_weight_t>::type WeightMap; | ||
| + | WeightMap weight_map = boost::get(boost::edge_weight, graph); | ||
| + | |||
| + | std::vector<Edge> mst_edges; | ||
| + | |||
| + | boost::graph::distributed::dense_boruvka_minimum_spanning_tree( | ||
| + | boost::graph::make_vertex_list_adaptor(graph), | ||
| + | weight_map, | ||
| + | std::back_inserter(mst_edges) | ||
| + | ); | ||
| + | |||
| + | if (process_id(graph.process_group()) == 0) | ||
| + | std::cout << "Finished" << std::endl; | ||
| + | } | ||
| + | </source> | ||
| + | |||
| + | К сожалению, не удалось запустить программу, использующую данную библиотеку на суперкомпьютере IBM BlueGene/P, поэтому замеры производительности производились на компьютере с процессором Intel Core i5 4210U (два ядра и четыре потока, тактовая частота 1.7ГГц, до 2.7ГГц в режиме Turbo Boost), 6GB оперативной памяти DDR3, жёстким диском с частотой вращения шпинделя 5400 об/мин под управлением Windows 10 64-bit с использованием Windows Subsystem for Linux. | ||
| + | |||
| + | На графике представлена зависимость времени работы программы на случайном полном графе из 5000 вершин (соответствует набору из 5000 точек для кластеризации) от количества доступных процессоров, а также ожидаемое время работы на этом же количестве процессоров. | ||
| + | |||
| + | Замеры производились только для построения минимального остовного дерева для полного графа (вершины — объекты, рёбра с весами — отношения), так как это является вычислительным ядром алгоритма. | ||
| + | |||
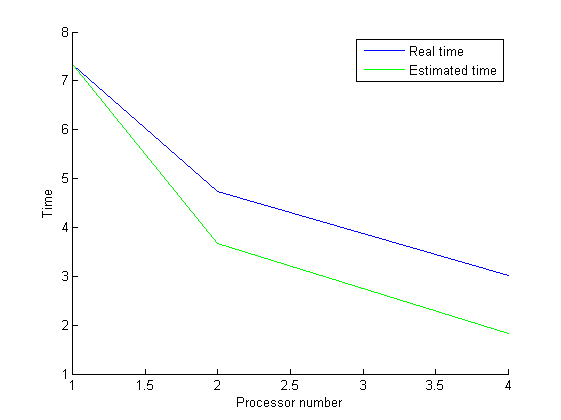
| + | [[File:boost_mst_time.png|frame|center|alt=Время работы|Время работы алгоритма построения MST на полном графе из 5000 вершин, синем показана полученное время работы в секундах, зелёным — ожидаемое относительно увеличения количества процессором]] | ||
| + | |||
| + | Более подробную информацию о производительности этого и других алгоритмов из Boost/graph/distributed можно получить на их странице: http://www.boost.org/doc/libs/1_55_0/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#performance. | ||
| + | |||
| + | === Динамические характеристики и эффективность реализации алгоритма === | ||
| + | |||
| + | === Выводы для классов архитектур === | ||
| + | |||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | Библиотека шаблонов для С++ Boost предлагает прямую параллельную реализацию алгоритма Борувки в компоненте graph/distributed. Кроме этого, в ней имеются реализации других алгоритмов построения MST, а также много других параллельных алгоритмов на графах. Библиотека основана на технологии MPI. IBM предоставил патч для Boost 1.47.0 для её использования с компиляторами IBM CL C/C++. | ||
| + | |||
| + | Кроме этой библиотеки не существует распространённой библиотеки, реализующей параллельный алгоритм построения минимального остовного дерева. Но имеется достаточно большое количество библиотек, реализующих однопоточное построение MST: | ||
| + | * JGraphT для Java | ||
| + | * SciPy MST | ||
| + | * множество любительских реализаций, который можно легко найти в интернете по запросу "mst algorithm". | ||
== Литература == | == Литература == | ||
| + | # Нейский И.М. Классификация и сравнение методов кластеризации, http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf | ||
| + | # Minimum spanning tree, https://en.wikipedia.org/wiki/Minimum_spanning_tree | ||
| + | # Алгоритм Борувки, https://en.wikipedia.org/wiki/Bor%C5%AFvka%27s_algorithm | ||
| + | # Euclidean minimum spanning tree, https://en.wikipedia.org/wiki/Euclidean_minimum_spanning_tree | ||
| + | # Система непересекающихся множеств, http://e-maxx.ru/algo/dsu | ||
| + | # Boost Library, http://www.boost.org/ | ||
| + | # Параллельное построение MST в библиотеке Boost, http://www.boost.org/doc/libs/1_55_0/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#id14 | ||
| + | # Патч Boost 1.47.0 для IBM CL C/C++, http://www-01.ibm.com/support/docview.wss?uid=swg27027469 | ||
Текущая версия на 12:55, 17 декабря 2016
Содержание
- 1 Структура и свойства алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Структура и свойства алгоритма
1.1 Общее описание алгоритма
Кластеризация — это задача статистического анализа, состоящая в разбиении множества объектов на группы, называемые кластерами, внутри которых объекты обладают похожими свойствами (чаще всего, это означает близость относительно заданной метрики). Изначально группы неизвестны, в зависимости от постановки задачи может быть также известно или неизвестно общее число кластеров.
Постановка задачи также может различаться характером входных данных:
- Набор признаков [math] V = \left\{ v_1, v_2, \ldots, v_N \right\} [/math] в некотором метрическом пространстве с метрикой [math] \rho(x, y) [/math]
- Матрица отношений между объектами: симметричная матрица вещественных чисел размером [math] N \times N [/math] с неотрицательными элементами с нулевой диагональю.
В данной статье рассматривается постановка с известным количеством кластеров [math] K [/math].
В данной статье рассматривается алгоритм алгоритм кластеризации на основе MST (Minimum spanning tree — минимальное остовное дерево).
Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.
Общая схема алгоритма:
- Построение минимального остовного дерева одним из известных методов (алгоритмы Крускала, Прима, Борувки и их комбинации; наиболее пригодным для параллельного исполнения считается алгоритм Борувки)
- Удаление [math] K-1 [/math] самых длинных рёбер из минимального остовного дерева.
В данной статье рассматривается версия алгоритма с использованием алгоритма Борувки.
В случае постановки задачи в виде набора признаков в подходящем метрическом пространстве возможна также предварительная подготовка графа, состоящая из построения триангуляции Делоне. Так как любое минимальное остовное дерево в этом случае принадлежит триангуляции Делоне, в некоторых случаях это позволяет значительно улучшить ассимптотику алгоритма. Данная часть алгоритма не является обязательной, поэтому подробно рассматриваться не будет.
1.2 Математическое описание алгоритма
Пусть [math]V[/math] — множество объектов, [math]Y[/math] — множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами [math]\rho(x,y)[/math]. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике [math]\rho[/math], а объекты разных кластеров существенно отличались. При этом каждому объекту [math]v_i\in V[/math] приписывается номер кластера [math]y_i[/math].
Алгоритм кластеризации — это функция [math]a\colon V\to Y[/math], которая любому объекту [math]v\in V[/math] ставит в соответствие номер кластера [math]y\in Y[/math]. Множество [math]Y[/math] в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
В данном случае задачу можно сформулировать так: выбрать пороговое значение веса ребра [math]W[/math], так чтобы объекты, соединённые ребром весом меньше [math]W[/math] лежали в одном кластере, а соединённые ребром весом больше [math]W[/math] — в разных.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является построение минимального остовного дерева для графа отношений с помощью алгоритма Борувки. В некоторых случаях построение минимального остовного дерева имеет ту же сложность, что и предварительное построение триангуляции Делоне, если оно используется.
1.4 Макроструктура алгоритма
Основной алгоритм можно разделить на следующие части:
- Нахождение для каждой вершины наименьшего ребра, инциндентного ней
- Добавление найденных наименьших вершин в MST
- "Склейка" компонент связности MST
- Нахождение веса [math]W_{K-1}[/math] [math](K-1)[/math]-ого наибольшего ребра
- Удаление рёбер весом не меньше чем [math]W_{K-1}[/math].
1.5 Схема реализации последовательного алгоритма
0 Ввод: граф V
1
2 Поместить каждую вершину в отдельное дерево леса T
3 Пока в T больше одной компоненты связности:
4 Для каждой компоненты C из T:
5 S — пустое множество рёбер
6 Для каждой вершины v в C:
7 Найти кратчайшее ребро с одним концом v, а другим не из C, и поместить его в S
8 Добавить кратчайшее ребро из S в T
9 Объединить компоненты связности
10 T — MST
11
12 Найти W — вес (K-1)-ого максимального ребра в T
13 Удалить из T рёбра с весом большим или равным W
14
15 Пронумеровать компоненты связности
16
17 Вывод: номера компонент связности для каждой вершины
1.6 Последовательная сложность алгоритма
- Нахождение ребер наименьшего веса для всех компонент связности требует [math]O(V)[/math] операций на каждом шаге, где [math]V[/math] — число рёбер в графе.
- Добавление новых рёбер в MST требует [math]O(N)[/math] операций за всё время работы алгоритма.
- При использовании структуры данных система непересекающихся множеств с ранговой эвристикой, объединение деревьев требует примерно , где [math]O(N)[/math] операций.
- Доказано, что количество шагов алгоритма [math]O(\log N)[/math].
Итого [math]O(V \log N)[/math] операций. При использовании триангуляции Делонэ в некоторых случаях [math]V[/math] имеет тот же порядок, что и [math]N[/math], поэтому общая сложность [math]O(N \log N)[/math]. В общем же случае сложность составляет [math]O(N^2 \log N)[/math]
Удаление [math]K-1[/math] рёбер можно осуществить за [math]O(N)[/math] операций.
Итак, общая сложность алгоритма в общем случае [math]O(N^2 \log N)[/math].
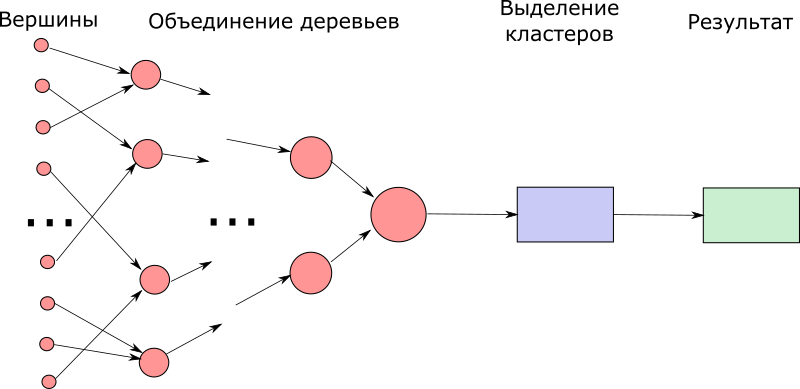
1.7 Информационный граф
Изначально все вершины находятся в своих собственных деревьях (стадия вершин). Затем с помощью нахождения кратчайших рёбер, соединяющих разные поддеревья, происходит слияние поддеревьев (стадия объединения деревьев) до тех пор, пока не останется одно дерево, являющееся минимальным остовным деревом исходного графа. После этого нужно будет лишь удалить нужное количество рёбер (выделение кластеров).
1.8 Ресурс параллелизма алгоритма
Основным местом для распараллеливания алгоритма является поиск наименьшего ребра из одной компоненты связности в другие. Так как компоненты связности в данном случае независимы, то отдельные узлы вычислительной системы могут выполнять поиск наименьших рёбер независимо.
Узким местом является нахождение k-ой порядковой статистики для выделения кластеров, а так же объединение компонент связности. Но всего объединений компонент связности [math]N-1[/math], поэтому при его реализации с помощью структуры данных система непересекабщихся множеств с ранговой эвристикой общая сложность за всё время работы алгоритма будет близко к [math]O(N)[/math].
1.9 Входные и выходные данные алгоритма
Входными данными являются число [math] N [/math] (количество элементов рассматриваемого множества) и матрица вещественных чисел размера [math] N \times N [/math] отношений между элементами этого множества. Матрица предполагается симметричной, а её диагональные элементы равными нулю, поэтому её размер можно оценить как [math] \tfrac{N(N-1)}{2} [/math].
Кроме того, имеется натуральное число [math] K \leqslant N [/math] — требуемое количество кластеров.
Выходными данными являются [math] N [/math] натуральных чисел от [math] 1 [/math] до [math] K [/math] — номера кластеров, в которые определена каждая вершина. При этом, каждый кластер содержит хотя бы одну вершину.
1.10 Свойства алгоритма
Отрицательной сторой алгоритмов кластеризации, основанных на минимальных остовных деревьях, является их чувствительность к выбросам. С другой стороны, эти алгоритмы способны выделять кластеры произвольной формы, а результат их применения интуитивно понятен.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
Интересной особенностью использования библиотеки Boost::graph::distributed является возможность задания изначального распределения вершин графа по процессам. К сложностям использования можно отнести нечитаемые сообщения об ошибках инстанцирования шаблонов С++ и отсутствие большого числа примеров использования библиотеки в интернете.
2.4 Масштабируемость алгоритма и его реализации
В этом параграфе описывается масштабируемость параллельной реализации алгоритма из библиотеки Boost::graph::distributed.
С использованием библиотеки Boost::graph::distributed программу можно реализовать следующим образом (указана только часть построения MST):
0 #include <boost/graph/use_mpi.hpp>
1 #include <boost/graph/distributed/mpi_process_group.hpp>
2 #include <boost/graph/distributed/adjacency_list.hpp>
3 #include <boost/graph/distributed/dehne_gotz_min_spanning_tree.hpp>
4 #include <boost/graph/distributed/vertex_list_adaptor.hpp>
5 #include <boost/graph/metis.hpp>
6
7 #include <iostream>
8 #include <fstream>
9 #include <vector>
10
11 typedef boost::adjacency_list<
12 boost::listS,
13 boost::distributedS<
14 boost::graph::distributed::mpi_process_group,
15 boost::vecS
16 >,
17 boost::undirectedS,
18 boost::no_property,
19 boost::property<
20 boost::edge_weight_t,
21 float
22 >
23 > Graph;
24
25 typedef boost::graph_traits<Graph>::edge_descriptor Edge;
26
27 int main(int argc, char* argv[])
28 {
29 boost::mpi::environment env(argc, argv);
30
31 std::ifstream in("big.graph");
32 boost::graph::metis_reader reader(in);
33
34 Graph graph(
35 reader.begin(), reader.end(),
36 reader.weight_begin(),
37 reader.num_vertices()
38 );
39
40 typedef boost::property_map<Graph, boost::edge_weight_t>::type WeightMap;
41 WeightMap weight_map = boost::get(boost::edge_weight, graph);
42
43 std::vector<Edge> mst_edges;
44
45 boost::graph::distributed::dense_boruvka_minimum_spanning_tree(
46 boost::graph::make_vertex_list_adaptor(graph),
47 weight_map,
48 std::back_inserter(mst_edges)
49 );
50
51 if (process_id(graph.process_group()) == 0)
52 std::cout << "Finished" << std::endl;
53 }
К сожалению, не удалось запустить программу, использующую данную библиотеку на суперкомпьютере IBM BlueGene/P, поэтому замеры производительности производились на компьютере с процессором Intel Core i5 4210U (два ядра и четыре потока, тактовая частота 1.7ГГц, до 2.7ГГц в режиме Turbo Boost), 6GB оперативной памяти DDR3, жёстким диском с частотой вращения шпинделя 5400 об/мин под управлением Windows 10 64-bit с использованием Windows Subsystem for Linux.
На графике представлена зависимость времени работы программы на случайном полном графе из 5000 вершин (соответствует набору из 5000 точек для кластеризации) от количества доступных процессоров, а также ожидаемое время работы на этом же количестве процессоров.
Замеры производились только для построения минимального остовного дерева для полного графа (вершины — объекты, рёбра с весами — отношения), так как это является вычислительным ядром алгоритма.
Более подробную информацию о производительности этого и других алгоритмов из Boost/graph/distributed можно получить на их странице: http://www.boost.org/doc/libs/1_55_0/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#performance.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Библиотека шаблонов для С++ Boost предлагает прямую параллельную реализацию алгоритма Борувки в компоненте graph/distributed. Кроме этого, в ней имеются реализации других алгоритмов построения MST, а также много других параллельных алгоритмов на графах. Библиотека основана на технологии MPI. IBM предоставил патч для Boost 1.47.0 для её использования с компиляторами IBM CL C/C++.
Кроме этой библиотеки не существует распространённой библиотеки, реализующей параллельный алгоритм построения минимального остовного дерева. Но имеется достаточно большое количество библиотек, реализующих однопоточное построение MST:
- JGraphT для Java
- SciPy MST
- множество любительских реализаций, который можно легко найти в интернете по запросу "mst algorithm".
3 Литература
- Нейский И.М. Классификация и сравнение методов кластеризации, http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf
- Minimum spanning tree, https://en.wikipedia.org/wiki/Minimum_spanning_tree
- Алгоритм Борувки, https://en.wikipedia.org/wiki/Bor%C5%AFvka%27s_algorithm
- Euclidean minimum spanning tree, https://en.wikipedia.org/wiki/Euclidean_minimum_spanning_tree
- Система непересекающихся множеств, http://e-maxx.ru/algo/dsu
- Boost Library, http://www.boost.org/
- Параллельное построение MST в библиотеке Boost, http://www.boost.org/doc/libs/1_55_0/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#id14
- Патч Boost 1.47.0 для IBM CL C/C++, http://www-01.ibm.com/support/docview.wss?uid=swg27027469