Участник:Demon smd/Нечеткий алгоритм С средних: различия между версиями
Demon smd (обсуждение | вклад) |
|||
| (не показано 80 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|Coctic}} | ||
| + | |||
{{algorithm | {{algorithm | ||
| name = Нечеткий алгоритм C средних (Fuzzy C-means) | | name = Нечеткий алгоритм C средних (Fuzzy C-means) | ||
| − | | serial_complexity = <math> | + | | serial_complexity = <math>O(C^2*|X|*D*IterNumber)</math> |
| − | | pf_height = <math> | + | | pf_height = <math>O(\log_{2}C^4*|X|^3) * IterNumber</math> |
| − | | pf_width = <math> | + | | pf_width = <math>O(C^2*|X|)</math> |
| − | | input_data = <math> | + | | input_data = <math>|X|*p</math>, где <math>p</math> - размерность входных векторов |
| − | | output_data = <math> | + | | output_data = <math>|X|*C </math> |
}} | }} | ||
| − | Авторы описания алгоритма: [[Участник:Demon smd|Д.А.Гуськов]] [[Участник:marina abramenkova|М.А.Абраменкова]] | + | Авторы описания алгоритма: |
| + | [[Участник:Demon smd|Д.А.Гуськов]] | ||
| + | [[Участник:marina abramenkova|М.А.Абраменкова]]. | ||
| + | Во все разделы вклад равноценный. | ||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 17: | Строка 22: | ||
и усовершенствован (для случая m>1) | и усовершенствован (для случая m>1) | ||
J.C. Bezdek в 1981 г. <ref>Bezdek, James C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. ISBN 0-306-40671-3.</ref> | J.C. Bezdek в 1981 г. <ref>Bezdek, James C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. ISBN 0-306-40671-3.</ref> | ||
| − | . В отличие от алгоритма c-means | + | . В отличие от алгоритма c-means данный метод кластеризации предполагает, что входные данные могут принадлежать более, чем одному кластеру одновременно. |
| − | Алгоритм получает на вход набор | + | Алгоритм получает на вход набор кластеризуемых векторов, количество кластеров, коэффициент неопределённости m и коэффициент <math>\varepsilon > 0</math>, определяющий точность алгоритма. На выходе алгоритма получаем матрицу вероятностей принадлежности каждого входного вектора каждому кластеру. |
| − | Нечеткий алгоритм С средних для каждого вектора | + | Нечеткий алгоритм С средних заключается в следующем. Изначально для каждого вектора определяется случайным образом вероятность принадлежности вектора к каждому кластеру. Далее запускается итерационный процесс, на каждой итерации которого происходит: |
| − | 1) | + | 1) расчёт центров кластеров |
| − | 2) | + | 2) расчёт Евклидова расстояния от каждого вектора до центра каждого кластера |
| − | 3) | + | 3) расчёт и нормализация коэффициентов принадлежности векторов кластерам |
| − | 4) | + | 4) расчёт значения решающей функции и сравнение этого значения со значением решающей функции на предшествующей итерации: если разница этих значений меньше установленного значения, то алгоритм прекращает работу (решающая функция возвращает сумму всех Евклидовых расстояний каждого объекта к каждому центру кластера умноженному на коэффициент принадлежности) |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 34: | Строка 39: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | + | \sum_{i = 1}^{|X|}\sum_{j = 1}^{C}u_{i,j}^m\left\Vert{x_{i}-c_{j}}\right\|^2 & , & & 1 \le m \le \infty , \\ | |
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | + | где m - это действительное число не меньше единицы, <math>u_{i,j}</math> - коэффициент принадлежности вектора <math>x_{i}</math> к кластеру <math>c_{j}</math>, <math>x_{i}</math> - <math>i</math>-ый компонент <math>|X|</math>-мерного вектора <math>X</math>, <math>C</math> - количество кластеров, <math>c_{j}</math> | |
| − | где m - это действительное число не меньше единицы, <math>u_{i,j}</math> - коэффициент принадлежности вектора <math>x_{i}</math> к кластеру <math>c_{j}</math>, <math>x_{i}</math> - <math>i</math>-ый компонент <math> | ||
- центр <math>j</math>-ого кластера, а <math>\left\Vert{*}\right\|</math> - это любая норма, определяющая расстояние от вектора до центра кластера. | - центр <math>j</math>-ого кластера, а <math>\left\Vert{*}\right\|</math> - это любая норма, определяющая расстояние от вектора до центра кластера. | ||
Нечёткое разбиение входных данных на кластеры производится итеративной оптимизацией вышеуказанной функции с обновлением коэффициента принадлежности <math>u_{i,j}</math> и переопределением центра кластера <math>c_{j}</math> на каждой итерации алгоритма. | Нечёткое разбиение входных данных на кластеры производится итеративной оптимизацией вышеуказанной функции с обновлением коэффициента принадлежности <math>u_{i,j}</math> и переопределением центра кластера <math>c_{j}</math> на каждой итерации алгоритма. | ||
| Строка 44: | Строка 48: | ||
==== Вычисляемые данные на каждой итерации ==== | ==== Вычисляемые данные на каждой итерации ==== | ||
* Центры кластеров рассчитываются по следующей формуле: <math>c_{j} = {{\sum_{i = 1}^{n}{u_{i,j}^m} * x_{i}} \over {\sum_{i = 1}^{n}{u_{i,j}^m}}}</math>, где <math>u_{i,j}</math> — коэффициент принадлежности <math>x_{i}</math> вектора к кластеру <math>c_{j}</math>. | * Центры кластеров рассчитываются по следующей формуле: <math>c_{j} = {{\sum_{i = 1}^{n}{u_{i,j}^m} * x_{i}} \over {\sum_{i = 1}^{n}{u_{i,j}^m}}}</math>, где <math>u_{i,j}</math> — коэффициент принадлежности <math>x_{i}</math> вектора к кластеру <math>c_{j}</math>. | ||
| − | |||
| − | |||
* Коэффициент принадлежности рассчитывается по формуле: <math>u_{i,j} = {1 \over \sum_{k = 1}^{C}{({\left\Vert{x_{i}-c_{j}}\right\| \over \left\Vert{x_{i}-c_{k}}\right\|})}^{2 \over m-1}}</math> | * Коэффициент принадлежности рассчитывается по формуле: <math>u_{i,j} = {1 \over \sum_{k = 1}^{C}{({\left\Vert{x_{i}-c_{j}}\right\| \over \left\Vert{x_{i}-c_{k}}\right\|})}^{2 \over m-1}}</math> | ||
| − | |||
| − | |||
* Решающая функция рассчитывается по формуле: <math>\max_{i,j}(|u_{i,j}^{(k)} - u_{i,j}^{(k-1)}|)</math>, где <math>k</math> - номер итерации алгоритма | * Решающая функция рассчитывается по формуле: <math>\max_{i,j}(|u_{i,j}^{(k)} - u_{i,j}^{(k-1)}|)</math>, где <math>k</math> - номер итерации алгоритма | ||
| Строка 55: | Строка 55: | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | + | Ядром алгоритма является: | |
| + | * вычисление новых центров кластеров | ||
| + | * для каждого входного вектора вычисление Евклидова расстояния до центров кластеров, а также коэффициента принадлежности кластерам | ||
| + | * вычисление решающей функции | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| + | |||
| + | В каждой итерации алгоритма происходит 3 основных действия описанных в п. 1.2.1: | ||
| + | *вычисление центров кластеров | ||
| + | *вычисление коэффициентов принадлежности | ||
| + | *вычисление решающей функции | ||
| + | Подробное описание макроструктур в виде кода приведено в пункте 1.5 | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| Строка 65: | Строка 74: | ||
<source lang="C++"> | <source lang="C++"> | ||
| − | FCM (X[], C | + | FCM (X[], C, m, eps){ |
float deside = 0; | float deside = 0; | ||
float newDeside = 0; | float newDeside = 0; | ||
| Строка 76: | Строка 85: | ||
float numerator = 0; | float numerator = 0; | ||
float denumerator = 0; | float denumerator = 0; | ||
| − | for (int i=0; i<X; i++){ //для каждого вектора | + | for (int i=0; i<X.size(); i++){ //для каждого вектора |
numerator+=pow(u[i][j], m) * x[i]; | numerator+=pow(u[i][j], m) * x[i]; | ||
denumerator+=pow(u[i][j], m); | denumerator+=pow(u[i][j], m); | ||
| Строка 84: | Строка 93: | ||
//вычисление коэффициентов u[][] | //вычисление коэффициентов u[][] | ||
| − | for (int i=0; i<X; i++) //для каждого вектора | + | for (int i=0; i<X.size(); i++) //для каждого вектора |
for (int j=0; j<C; j++){ //для каждого кластера | for (int j=0; j<C; j++){ //для каждого кластера | ||
sum = 0; | sum = 0; | ||
| Строка 94: | Строка 103: | ||
//определения максимального различия между u[][] и uPrev[][] | //определения максимального различия между u[][] и uPrev[][] | ||
float max = 0; | float max = 0; | ||
| − | for (int i=0; i<X; i++) //для каждого вектора | + | for (int i=0; i<X.size(); i++) //для каждого вектора |
for (int j=0; j<C; j++){ //для каждого кластера | for (int j=0; j<C; j++){ //для каждого кластера | ||
if (abs(uPrev[i][j]-u[i][j])>max) | if (abs(uPrev[i][j]-u[i][j])>max) | ||
| Строка 100: | Строка 109: | ||
if (eps <= max) | if (eps <= max) | ||
| − | for (int i=0; i<X; i++) //для каждого вектора | + | for (int i=0; i<X.size(); i++) //для каждого вектора |
for (int j=0; j<C; j++){ //для каждого кластера | for (int j=0; j<C; j++){ //для каждого кластера | ||
uPrev[i][j]=u[i][j]; | uPrev[i][j]=u[i][j]; | ||
| Строка 113: | Строка 122: | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| − | Последовательная сложность всего алгоритма складывается из сложности операций на каждой итерации умноженную на количество итераций. Так как в данном алгоритме количество итераций не является фиксированным и зависит от: | + | Последовательная сложность всего алгоритма складывается из сложности операций на каждой итерации умноженную на количество итераций. |
| + | Под операцией будем понимать выражение в языке с++ из пункта 1.5, находящееся в теле цикла (например, выражения "sum+= pow( dist(x[i], c[j]) / dist(x[i], c[k]), 2/(m-1));" или "uPrev[i][j]=u[i][j];" считаются за одну операцию). Так как при больших входных объёмах данных сложность алгоритма в большей степени зависит от количества входных данных, и незначительно зависит от сложности операций,то при оценке сложности алгоритма сложность выражений можно считать равной единице. Так как в данном алгоритме количество итераций не является фиксированным и зависит от: | ||
* параметра <math>\varepsilon</math> | * параметра <math>\varepsilon</math> | ||
* набора входных векторов <math>x</math> | * набора входных векторов <math>x</math> | ||
* выбора начальных коэффициентов <math>u</math> | * выбора начальных коэффициентов <math>u</math> | ||
то в данном пункте будет приведена сложность одной итерации относительно количества входных векторов. | то в данном пункте будет приведена сложность одной итерации относительно количества входных векторов. | ||
| − | + | Для вычисления коэффициентов u[][] на каждой итерации алгоритма требуется определить расстояние от векторов до центра кластера. Сложность данной операции зависит от размерности входных данных и определении нормы. В виду того, что для разных задач могут быть введены разные нормы, и сложность вычисления расстояний может варьироваться, то в данной статье будем считать, что сложность вычисления расстояния зависит линейно от размерности водных данных. В таком случае, для вычисления центров кластеров требуется <math>O(2*C*|X|)</math> операций, для определения коэффициентов <math>u</math> - <math>O(C^2*|X|*D)</math> операций, а для вычисления решающей функции - <math>O(2*C*|X|)</math> операций, где <math>|X|</math> - число входных векторов, а <math>C</math> - количество кластеров. | |
| − | Таким образом итоговая сложность одной итерации составляет <math>O( | + | |
| + | Таким образом итоговая сложность одной итерации составляет <math>O(C^2*|X|*D)</math>. | ||
=== Информационный граф === | === Информационный граф === | ||
| + | |||
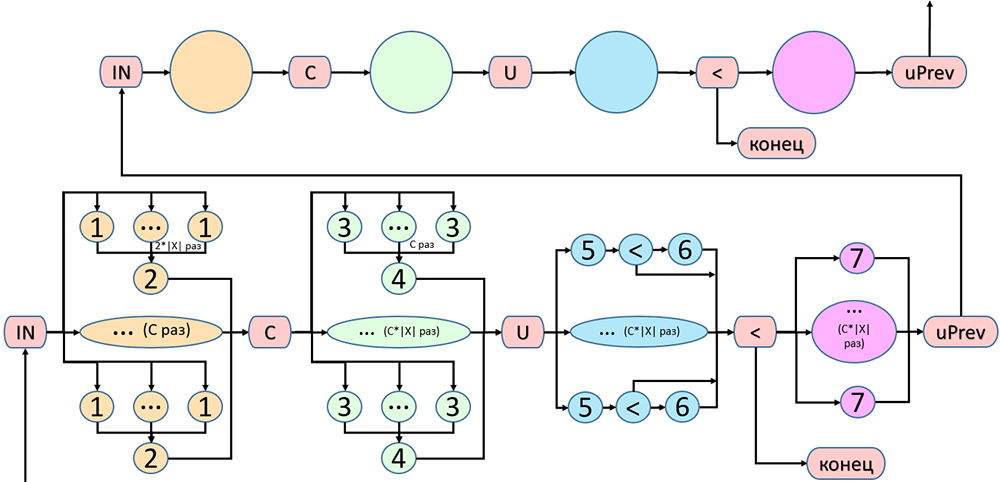
| + | Как видно из пункта 1.5, на каждом действии каждой итерации алгоритма все операции, выполняющиеся в цикле, не зависят друг от друга и могут быть распараллелены. Это показано на Рисунке 1. | ||
| + | |||
| + | [[File:FCMIG.png|thumb|center|1200px|Рисунок 1. Информационный граф алгоритма. (1)-(7) - это наборы последовательных действий (например, (2) - последовательные операции деления, чтения элемента из памяти и присваивания).]] | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | |||
| + | На каждом ярусе ярусно-параллельной формы алгоритма будет располагаться конечное число элементарных операций, например, чтение элемента из памяти, сложение или возведение в степень. Информационый граф из п.1.7 изображает свёрнутую ярусно-параллельную форму алгоритма. | ||
| + | |||
| + | Сложность алгоритма будем рассчитывать в предположении, что число вычислительных ядер стремится к бесконечности. Как видно из информационного графа, параллельная сложность вычисления центров кластеров составляет <math>O(\log_{2}(C*|X|))</math>, вычисления коэффициентов принадлежности - <math>O(\log_{2}(C^2*|X|))</math>, а вычисления решающей функции - не больше чем <math>O(\log_{2} (C*|X|))</math>. | ||
| + | |||
| + | Таким образом параллельная сложность итерации алгоритма составляет <math>O(\log_{2} (C^4*|X|^3))</math>. | ||
| + | |||
| + | Так как задачи, решаемые в макроструктуре алгоритма могут быть сведены к задачам вычисления суммы элементов массива и максимального элемента массива, то на <math>i</math>-ом ярусе графа будет находиться <math>{N}\over{2^i}</math> операции, где N - количество элементов массива. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
==== Входные данные алгоритма ==== | ==== Входные данные алгоритма ==== | ||
| − | * <math> | + | * <math>X</math> - набор из <math>|X|</math> входных векторов длины <math>p</math> |
* <math>C</math> - количество кластеров | * <math>C</math> - количество кластеров | ||
* <math>m</math> - коэффициент неопределённости | * <math>m</math> - коэффициент неопределённости | ||
* <math>\varepsilon > 0</math> - коэффициент, определяющий точность алгоритма. | * <math>\varepsilon > 0</math> - коэффициент, определяющий точность алгоритма. | ||
| + | |||
| + | Объем входных данных: <math>|X|*p+3</math> | ||
==== Выходные данные алгоритма ==== | ==== Выходные данные алгоритма ==== | ||
* <math>u</math> - матрица принадлежности векторов кластерам | * <math>u</math> - матрица принадлежности векторов кластерам | ||
| + | |||
| + | Объем выходных данных: <math>|X|*C</math> | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| + | |||
| + | Увеличение скорости работы алгоритма при распараллеливании на бесконечном количестве процессоров составляет <math>O({{C^2*|X|}\over{\log_{2} (C^4*|X|^3)}})</math>. Например, для разбиения 1000 элементов на 10 кластеров производительность параллельного алгоритма будет в 2315 раз больше, а на 20 кластеров - уже в 8477 раз. | ||
| + | |||
| + | == Программная реализация алгоритма == | ||
| + | |||
| + | === Особенности реализации последовательного алгоритма === | ||
| + | |||
| + | === Локальность данных и вычислений === | ||
| + | |||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | |||
| + | === Масштабируемость алгоритма и его реализации === | ||
| + | |||
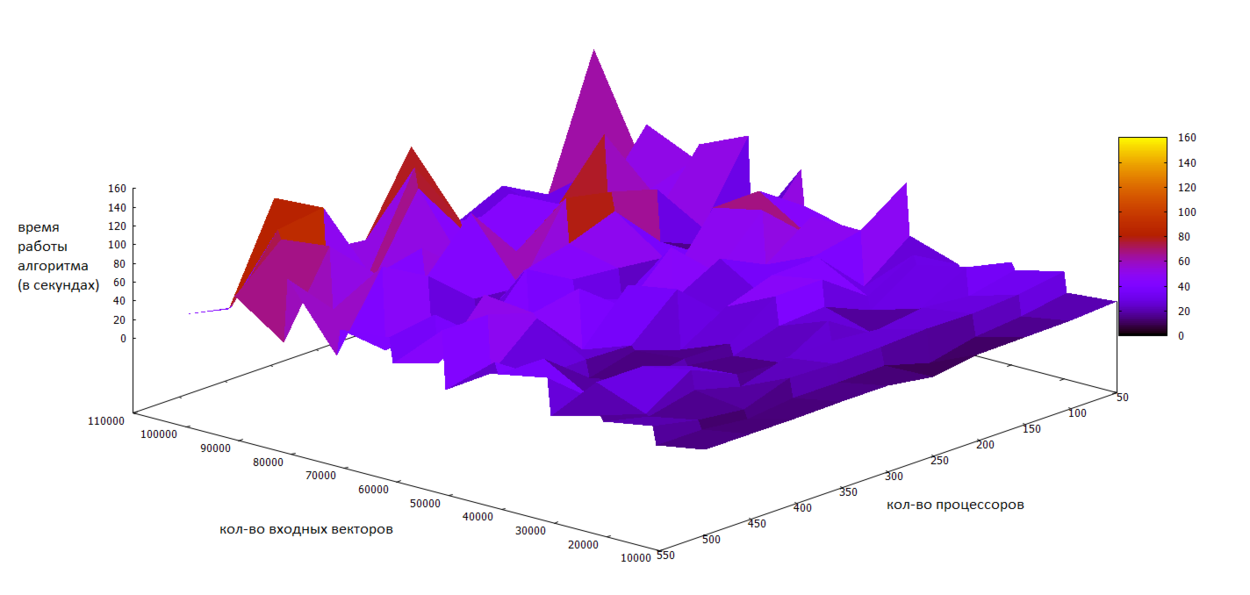
| + | Как видно из предыдущих пунктов, масштабируется данный алгоритм хорошо. С увеличением количества процессоров время работы падает, а с увеличением количества входных данных и количества кластеров - растёт. | ||
| + | На рисунках показаны результаты запусков алгоритма на разном количестве входных данных и процессоров на массивно-параллельной вычислительной системе Blue Gene/P. Использовался компилятор mpixlcxx без указания специфических опций. Запуски производились в режиме SMP (на каждом ядре 1 MPI процесс из 4 SMP нитей, 2 Гб памяти). Характеристики вычислительного узла: 4 ядерный 32-битный процессор PowerPC 850 Мгц. | ||
| + | |||
| + | Исходных код программы можно найти здесь: https://github.com/demonsmd/superPrak | ||
| + | [[File:FCMvectors_color2.png|thumb|center|1250px|Рисунок 2. Масштабируемость алгоритма. Зависимость времени работы алгоритма от количества процессоров и входных данных при фиксированном количестве кластеров.]] | ||
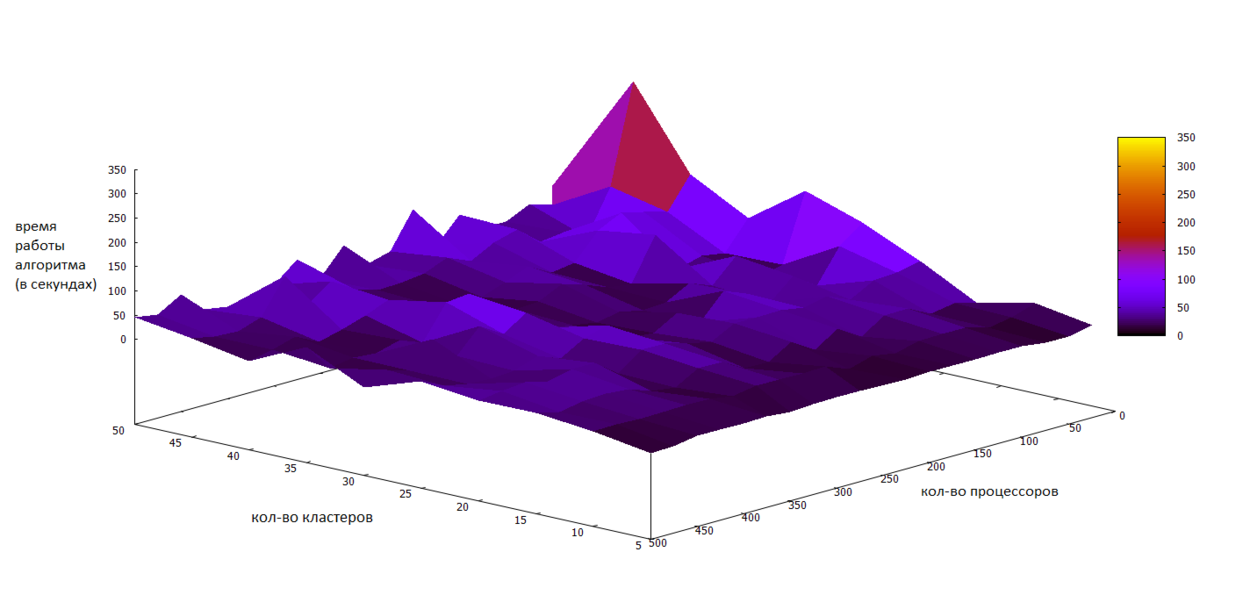
| + | [[File:FCMclusters_color.png|thumb|center|1250px|Рисунок 3. Масштабируемость алгоритма. Зависимость времени работы алгоритма от количества процессоров и кластеров при фиксированном количестве входных данных.]] | ||
| + | |||
| + | === Динамические характеристики и эффективность реализации алгоритма === | ||
| + | |||
| + | === Выводы для классов архитектур === | ||
| + | |||
| + | === Существующие реализации алгоритма === | ||
| + | |||
| + | Существует множество реализаций данного алгоритма. Рассмотрим некоторые из них: | ||
| + | |||
| + | - Например, тут: https://habrahabr.ru/post/208496/ | ||
| + | <ref>Нестер А. "Алгоритм нечёткой кластеризации fuzzy c-means на PHP". [html](https://habrahabr.ru/post/208496/)</ref> | ||
| + | приведено краткое описание алгоритма и приведена его реализация на php. В данной статье довольно подробно расписан каждый шаг алгоритма и приведён соответствующий ему фрагмент кода. | ||
| + | |||
| + | - Тут: http://num-meth.srcc.msu.ru/zhurnal/tom_2012/v13r207.html | ||
| + | <ref>Миниахметов Р.М., Цымблер М.Л. "Интеграция алгоритма кластеризации Fuzzy c-Means в PostgreSQL". [html](http://num-meth.srcc.msu.ru/zhurnal/tom_2012/v13r207.html)</ref> | ||
| + | приводится реализация алгоритма для PostgreSQL, а также прилагается скрипт внедрения алгоритма. | ||
== Литература == | == Литература == | ||
<references \> | <references \> | ||
Текущая версия на 00:13, 19 декабря 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 19.12.2016 Данная работа соответствует формальным критериям. Проверено Coctic. |
| Нечеткий алгоритм C средних (Fuzzy C-means) | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(C^2*|X|*D*IterNumber)[/math] |
| Объём входных данных | [math]|X|*p[/math], где [math]p[/math] - размерность входных векторов |
| Объём выходных данных | [math]|X|*C [/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(\log_{2}C^4*|X|^3) * IterNumber[/math] |
| Ширина ярусно-параллельной формы | [math]O(C^2*|X|)[/math] |
Авторы описания алгоритма:
Д.А.Гуськов
М.А.Абраменкова.
Во все разделы вклад равноценный.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Нечёткий алгоритм кластеризации С-средних был разработан (для случая m=2) J.C. Dunn в 1973 г. [1] и усовершенствован (для случая m>1) J.C. Bezdek в 1981 г. [2] . В отличие от алгоритма c-means данный метод кластеризации предполагает, что входные данные могут принадлежать более, чем одному кластеру одновременно. Алгоритм получает на вход набор кластеризуемых векторов, количество кластеров, коэффициент неопределённости m и коэффициент [math]\varepsilon \gt 0[/math], определяющий точность алгоритма. На выходе алгоритма получаем матрицу вероятностей принадлежности каждого входного вектора каждому кластеру.
Нечеткий алгоритм С средних заключается в следующем. Изначально для каждого вектора определяется случайным образом вероятность принадлежности вектора к каждому кластеру. Далее запускается итерационный процесс, на каждой итерации которого происходит:
1) расчёт центров кластеров
2) расчёт Евклидова расстояния от каждого вектора до центра каждого кластера
3) расчёт и нормализация коэффициентов принадлежности векторов кластерам
4) расчёт значения решающей функции и сравнение этого значения со значением решающей функции на предшествующей итерации: если разница этих значений меньше установленного значения, то алгоритм прекращает работу (решающая функция возвращает сумму всех Евклидовых расстояний каждого объекта к каждому центру кластера умноженному на коэффициент принадлежности)
1.2 Математическое описание алгоритма
Нечеткий алгоритм С средних минимизирует величину:
- [math] \begin{align} \sum_{i = 1}^{|X|}\sum_{j = 1}^{C}u_{i,j}^m\left\Vert{x_{i}-c_{j}}\right\|^2 & , & & 1 \le m \le \infty , \\ \end{align} [/math]
где m - это действительное число не меньше единицы, [math]u_{i,j}[/math] - коэффициент принадлежности вектора [math]x_{i}[/math] к кластеру [math]c_{j}[/math], [math]x_{i}[/math] - [math]i[/math]-ый компонент [math]|X|[/math]-мерного вектора [math]X[/math], [math]C[/math] - количество кластеров, [math]c_{j}[/math] - центр [math]j[/math]-ого кластера, а [math]\left\Vert{*}\right\|[/math] - это любая норма, определяющая расстояние от вектора до центра кластера. Нечёткое разбиение входных данных на кластеры производится итеративной оптимизацией вышеуказанной функции с обновлением коэффициента принадлежности [math]u_{i,j}[/math] и переопределением центра кластера [math]c_{j}[/math] на каждой итерации алгоритма.
1.2.1 Вычисляемые данные на каждой итерации
- Центры кластеров рассчитываются по следующей формуле: [math]c_{j} = {{\sum_{i = 1}^{n}{u_{i,j}^m} * x_{i}} \over {\sum_{i = 1}^{n}{u_{i,j}^m}}}[/math], где [math]u_{i,j}[/math] — коэффициент принадлежности [math]x_{i}[/math] вектора к кластеру [math]c_{j}[/math].
- Коэффициент принадлежности рассчитывается по формуле: [math]u_{i,j} = {1 \over \sum_{k = 1}^{C}{({\left\Vert{x_{i}-c_{j}}\right\| \over \left\Vert{x_{i}-c_{k}}\right\|})}^{2 \over m-1}}[/math]
- Решающая функция рассчитывается по формуле: [math]\max_{i,j}(|u_{i,j}^{(k)} - u_{i,j}^{(k-1)}|)[/math], где [math]k[/math] - номер итерации алгоритма
1.3 Вычислительное ядро алгоритма
Ядром алгоритма является:
- вычисление новых центров кластеров
- для каждого входного вектора вычисление Евклидова расстояния до центров кластеров, а также коэффициента принадлежности кластерам
- вычисление решающей функции
1.4 Макроструктура алгоритма
В каждой итерации алгоритма происходит 3 основных действия описанных в п. 1.2.1:
- вычисление центров кластеров
- вычисление коэффициентов принадлежности
- вычисление решающей функции
Подробное описание макроструктур в виде кода приведено в пункте 1.5
1.5 Схема реализации последовательного алгоритма
Схему реализации последовательного алгоритма можно описать на C++ следующим образом:
FCM (X[], C, m, eps){
float deside = 0;
float newDeside = 0;
generateMembershipDegree(); //заполняет uPrev[][] случайными нормрованными коэффициентами
while (true){
newDeside = deside;
//вычисление центров кластеров
for (int j=0; j<C; j++){ //для каждого кластера
float numerator = 0;
float denumerator = 0;
for (int i=0; i<X.size(); i++){ //для каждого вектора
numerator+=pow(u[i][j], m) * x[i];
denumerator+=pow(u[i][j], m);
}
c[j] = numerator / denumerator;
}
//вычисление коэффициентов u[][]
for (int i=0; i<X.size(); i++) //для каждого вектора
for (int j=0; j<C; j++){ //для каждого кластера
sum = 0;
for (int k=0; k<C; k++)
sum+= pow( dist(x[i], c[j]) / dist(x[i], c[k]), 2/(m-1));
u[i][j] = 1/sum
}
//определения максимального различия между u[][] и uPrev[][]
float max = 0;
for (int i=0; i<X.size(); i++) //для каждого вектора
for (int j=0; j<C; j++){ //для каждого кластера
if (abs(uPrev[i][j]-u[i][j])>max)
max = abs(uPrev[i][j]-u[i][j]);
if (eps <= max)
for (int i=0; i<X.size(); i++) //для каждого вектора
for (int j=0; j<C; j++){ //для каждого кластера
uPrev[i][j]=u[i][j];
else
break;
}
return u;
}
1.6 Последовательная сложность алгоритма
Последовательная сложность всего алгоритма складывается из сложности операций на каждой итерации умноженную на количество итераций. Под операцией будем понимать выражение в языке с++ из пункта 1.5, находящееся в теле цикла (например, выражения "sum+= pow( dist(x[i], c[j]) / dist(x[i], c[k]), 2/(m-1));" или "uPrev[i][j]=u[i][j];" считаются за одну операцию). Так как при больших входных объёмах данных сложность алгоритма в большей степени зависит от количества входных данных, и незначительно зависит от сложности операций,то при оценке сложности алгоритма сложность выражений можно считать равной единице. Так как в данном алгоритме количество итераций не является фиксированным и зависит от:
- параметра [math]\varepsilon[/math]
- набора входных векторов [math]x[/math]
- выбора начальных коэффициентов [math]u[/math]
то в данном пункте будет приведена сложность одной итерации относительно количества входных векторов. Для вычисления коэффициентов u[][] на каждой итерации алгоритма требуется определить расстояние от векторов до центра кластера. Сложность данной операции зависит от размерности входных данных и определении нормы. В виду того, что для разных задач могут быть введены разные нормы, и сложность вычисления расстояний может варьироваться, то в данной статье будем считать, что сложность вычисления расстояния зависит линейно от размерности водных данных. В таком случае, для вычисления центров кластеров требуется [math]O(2*C*|X|)[/math] операций, для определения коэффициентов [math]u[/math] - [math]O(C^2*|X|*D)[/math] операций, а для вычисления решающей функции - [math]O(2*C*|X|)[/math] операций, где [math]|X|[/math] - число входных векторов, а [math]C[/math] - количество кластеров.
Таким образом итоговая сложность одной итерации составляет [math]O(C^2*|X|*D)[/math].
1.7 Информационный граф
Как видно из пункта 1.5, на каждом действии каждой итерации алгоритма все операции, выполняющиеся в цикле, не зависят друг от друга и могут быть распараллелены. Это показано на Рисунке 1.
1.8 Ресурс параллелизма алгоритма
На каждом ярусе ярусно-параллельной формы алгоритма будет располагаться конечное число элементарных операций, например, чтение элемента из памяти, сложение или возведение в степень. Информационый граф из п.1.7 изображает свёрнутую ярусно-параллельную форму алгоритма.
Сложность алгоритма будем рассчитывать в предположении, что число вычислительных ядер стремится к бесконечности. Как видно из информационного графа, параллельная сложность вычисления центров кластеров составляет [math]O(\log_{2}(C*|X|))[/math], вычисления коэффициентов принадлежности - [math]O(\log_{2}(C^2*|X|))[/math], а вычисления решающей функции - не больше чем [math]O(\log_{2} (C*|X|))[/math].
Таким образом параллельная сложность итерации алгоритма составляет [math]O(\log_{2} (C^4*|X|^3))[/math].
Так как задачи, решаемые в макроструктуре алгоритма могут быть сведены к задачам вычисления суммы элементов массива и максимального элемента массива, то на [math]i[/math]-ом ярусе графа будет находиться [math]{N}\over{2^i}[/math] операции, где N - количество элементов массива.
1.9 Входные и выходные данные алгоритма
1.9.1 Входные данные алгоритма
- [math]X[/math] - набор из [math]|X|[/math] входных векторов длины [math]p[/math]
- [math]C[/math] - количество кластеров
- [math]m[/math] - коэффициент неопределённости
- [math]\varepsilon \gt 0[/math] - коэффициент, определяющий точность алгоритма.
Объем входных данных: [math]|X|*p+3[/math]
1.9.2 Выходные данные алгоритма
- [math]u[/math] - матрица принадлежности векторов кластерам
Объем выходных данных: [math]|X|*C[/math]
1.10 Свойства алгоритма
Увеличение скорости работы алгоритма при распараллеливании на бесконечном количестве процессоров составляет [math]O({{C^2*|X|}\over{\log_{2} (C^4*|X|^3)}})[/math]. Например, для разбиения 1000 элементов на 10 кластеров производительность параллельного алгоритма будет в 2315 раз больше, а на 20 кластеров - уже в 8477 раз.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Как видно из предыдущих пунктов, масштабируется данный алгоритм хорошо. С увеличением количества процессоров время работы падает, а с увеличением количества входных данных и количества кластеров - растёт. На рисунках показаны результаты запусков алгоритма на разном количестве входных данных и процессоров на массивно-параллельной вычислительной системе Blue Gene/P. Использовался компилятор mpixlcxx без указания специфических опций. Запуски производились в режиме SMP (на каждом ядре 1 MPI процесс из 4 SMP нитей, 2 Гб памяти). Характеристики вычислительного узла: 4 ядерный 32-битный процессор PowerPC 850 Мгц.
Исходных код программы можно найти здесь: https://github.com/demonsmd/superPrak
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существует множество реализаций данного алгоритма. Рассмотрим некоторые из них:
- Например, тут: https://habrahabr.ru/post/208496/ [3] приведено краткое описание алгоритма и приведена его реализация на php. В данной статье довольно подробно расписан каждый шаг алгоритма и приведён соответствующий ему фрагмент кода.
- Тут: http://num-meth.srcc.msu.ru/zhurnal/tom_2012/v13r207.html [4] приводится реализация алгоритма для PostgreSQL, а также прилагается скрипт внедрения алгоритма.
3 Литература
<references \>
- ↑ Dunn, J. C. (1973-01-01). "A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters". Journal of Cybernetics. 3 (3): 32–57. doi:10.1080/01969727308546046. ISSN 0022-0280.
- ↑ Bezdek, James C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. ISBN 0-306-40671-3.
- ↑ Нестер А. "Алгоритм нечёткой кластеризации fuzzy c-means на PHP". [html](https://habrahabr.ru/post/208496/)
- ↑ Миниахметов Р.М., Цымблер М.Л. "Интеграция алгоритма кластеризации Fuzzy c-Means в PostgreSQL". [html](http://num-meth.srcc.msu.ru/zhurnal/tom_2012/v13r207.html)