Участник:Казаков Артем/Алгоритм концептуальной кластеризации COBWEB: различия между версиями
ASA (обсуждение | вклад) |
|||
| (не показана 81 промежуточная версия 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Assignment|ASA|Dexter}} | |
| − | + | {{algorithm | |
| + | | name = Алгоритм концептуальной кластеризации COBWEB | ||
| + | | serial_complexity = <math>O(N*logN*B^{2}AV)</math> | ||
| + | | parallel_complexity = <math>O(N*logN*log(BAV))</math> | ||
| + | }} | ||
| + | |||
| + | Автор статьи: [[Участник: Казаков Артем|Артем Казаков]] (группа 624) | ||
= ЧАСТЬ. Свойства и структура алгоритмов = | = ЧАСТЬ. Свойства и структура алгоритмов = | ||
== Общее описание алгоритма == | == Общее описание алгоритма == | ||
| − | Алгоритм COBWEB | + | Алгоритм '''COBWEB'''<ref name="wiki" /><ref name="paper" /> — классический метод инкрементальной концептуальной кластеризации. Он создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт (концепт — описание группы объектов через определенный набор пар аттрибут-значение) и содержит вероятностное описание этого концепта, которое включает в себя вероятность принадлежности концепта к данному узлу.<ref name="habr" /> |
| − | Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории | + | Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории — прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. Чтобы встроить новый объект в дерево классификации, алгоритм '''COBWEB''' итеративно проходит всё дерево в поисках «лучшего» узла, к которому отнести этот объект. Выбор узла осуществляется на основе помещения объекта в каждый узел и вычисления полезности категории получившегося среза. Также вычисляется полезность категории для случая, когда объект относится к вновь создаваемому узлу. В итоге объект относится к тому узлу, для которого полезность категории наибольшая. |
| − | Однако COBWEB имеет ряд ограничений. Во-первых, он предполагает, что распределения вероятностей значений различных атрибутов статистически независимы друг от друга. Однако это предположение не всегда верно, потому как часто между значениями атрибутов существует корреляция. Во-вторых, вероятностное представление кластеров делает очень сложным их обновление, особенно в том случае, когда атрибуты имеют большое число возможных значений. Это вызвано тем, что сложность алгоритма зависит не только от количества атрибутов, но и от количества их возможных значений. | + | Однако '''COBWEB''' имеет ряд ограничений. Во-первых, он предполагает, что распределения вероятностей значений различных атрибутов статистически независимы друг от друга. Однако это предположение не всегда верно, потому как часто между значениями атрибутов существует корреляция. Во-вторых, вероятностное представление кластеров делает очень сложным их обновление, особенно в том случае, когда атрибуты имеют большое число возможных значений. Это вызвано тем, что сложность алгоритма зависит не только от количества атрибутов, но и от количества их возможных значений. |
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| − | + | Обозначим: | |
| + | * <math>\{ A_{1}, A_{2}, ... \}</math> — множество свойств кластеризуемых объектов | ||
| + | * <math>\{ u_{1j}, u_{2j}, ... \}</math> — возможнные значения свойства <math>A_{j}</math> | ||
| + | * <math>\{ C_{1}, C_{2}, ... \}</math> — множество категорий | ||
| − | P( | + | <math>P(A_j = u_{ij} | C_k)</math> — это условная вероятность, с которой свойство <math>A_{j}</math>, принимает значение <math>u_{ij}</math>, если объект относится к категории <math>C_{k}</math>. Для каждой категории в иерархии определены вероятности вхождения всех значений каждого свойства. При предъявлении нового экземпляра система '''COBWEB''' оценивает качество отнесения этого примера к существующей категории и модификации иерархии категорий в соответствии с новым представителем. Критерием оценки качества классификации является полезность категории (''category utility''). |
Критерий полезности категории максимизирует вероятность того, что два объекта, отнесенные к одной категории, имеют одинаковые значения свойств и значения свойств для объектов из различных категорий отличаются. Полезность категории определяется формулой | Критерий полезности категории максимизирует вероятность того, что два объекта, отнесенные к одной категории, имеют одинаковые значения свойств и значения свойств для объектов из различных категорий отличаются. Полезность категории определяется формулой | ||
| − | <math>CU = \sum_{k} \sum_{i} \sum_{j} P( | + | <math>CU = \sum_{k} \sum_{i} \sum_{j} P(A_j = u_{ij}|C_k) P(C_k|A_j = u_{ij}) P(A_j = u_{ij})</math><ref name="shit" /> |
| − | Значения суммируются по всем категориям | + | Значения суммируются по всем категориям <math>C_k</math>, всем свойствам <math>A_j</math> и всем значениям свойств <math>u_{ij}</math>. Значение <math>P(A_j = u_{ij} | C_k)</math> называется предсказуемостью (predictability). Это вероятность того, что объект, для которого свойство <math>A_j</math> принимает значение <math>u_{ij}</math>, относится к категории <math>C_k</math>. Чем выше это значение, тем вероятнее, что свойства двух объектов, отнесенных к одной категории, имеют одинаковые значения. Величина <math>P(C_k | A = u_{ij})</math> называется предиктивностью (predictiveness). Это вероятность того, что для объектов из категории <math>C_k</math> свойство <math>A_j</math> принимает значение <math>u_{ij}</math>. Чем больше эта величина, тем менее вероятно, что для объектов, не относящихся к данной категории, это свойство будет принимать указанное значение. Значение <math>P(A = u_{ij})</math> — это весовой коэффициент, усиливающий влияние наиболее распространенных свойств. Благодаря совместному учету этих значений высокая полезность категории означает высокую вероятность того, что объекты из одной категории обладают одинаковыми свойствами, и низкую вероятность наличия этих свойств у объектов из других категорий. |
| + | |||
| + | == Вычислительное ядро алгоритма == | ||
| + | Основное время работы алгоритма приходится на вычисление полезности категории. | ||
| − | + | Обозначим: | |
| − | <math> | + | * <math>B</math> — среднее число потомков узлов в дереве классификации |
| + | * <math>N</math> — число объектов для классификации | ||
| + | * <math>A</math> — числа свойств у классифицируемых объектов | ||
| + | * <math>V</math> — среднее число значений, которые могут принимать свойства | ||
| + | На каждом шаге алгоритма (всего <math>N</math> производится спуск по дереву (<math>O(log_{B}N)</math>). На каждой итерации спуска производится <math>O(B)</math> вычислений полезности категории <math>CU</math>, вычисление каждой из которых имеет сложность <math>O(BAV)</math>. | ||
| − | + | Перемножив сложности выше получам сложность из п. 1.6., что подтверждает, что основная часть вычислительных операций приходится именно на вычисление полезностей категорий. | |
| − | |||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| − | + | В алгоритме '''COBWEB''' реализован метод поиска экстремума в пространстве возможных кластеров с использованием критерия полезности категорий для оценки и выбора возможных способов категоризации. | |
| − | + | * Сначала вводится единственная категория, свойства которой совпадают со свойствами первого экземпляра. | |
| − | + | * Для каждого последующего экземпляра алгоритм начинает свою работу с корневой категории и движется далее по дереву. | |
| + | * На каждом уровне выполняется оценка эффективности категоризации на основе полезности категории. При этом оцениваются результаты следующих операций: | ||
| + | ** Отнесение экземпляра к наилучшей из существующих категорий. | ||
| + | ** Добавление новой категории, содержащей единственный экземпляр. | ||
| + | ** Слияние двух существующих категорий в одну новую с добавлением в нее этого экземпляра. | ||
| + | ** Разбиение существующей категории на две и отнесение экземпляра к лучшей из вновь созданных категорий. | ||
| + | * Для слияния двух узлов создается новый узел, для которого существующие узлы становятся дочерними. На основе значений вероятностей дочерних узлов вычисляются вероятности для нового узла. При разбиении один узел заменяется двумя дочерними. | ||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| − | + | Алгоритм повторяется для каждого нового объекта. В данном алгоритме происходит спуск по дереву и на каждом шаге спуска выбирается одно из действий описанных в п. 1.4. | |
| − | cobweb(Node, Instance) | + | |
| + | <pre>cobweb(Node, Instance) | ||
Begin | Begin | ||
if узел Node - это лист, then | if узел Node - это лист, then | ||
| Строка 75: | Строка 97: | ||
cobweb(Cm, Instance) | cobweb(Cm, Instance) | ||
end; | end; | ||
| − | end | + | end</pre> |
| − | |||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| − | + | Последовательная сложность алгоритма равна <math>O(N*log_{B}N*B^{2}AV)</math> | |
| + | |||
| + | где: | ||
| + | * <math>B</math> — среднее число потомков узлов в дереве классификации | ||
| + | * <math>N</math> — число объектов для классификации | ||
| + | * <math>A</math> — числа свойств у классифицируемых объектов | ||
| + | * <math>V</math> — среднее число значений, которые могут принимать свойства | ||
| + | |||
| + | Обоснование сложности приводится в п. 1.3. | ||
== Информационный граф == | == Информационный граф == | ||
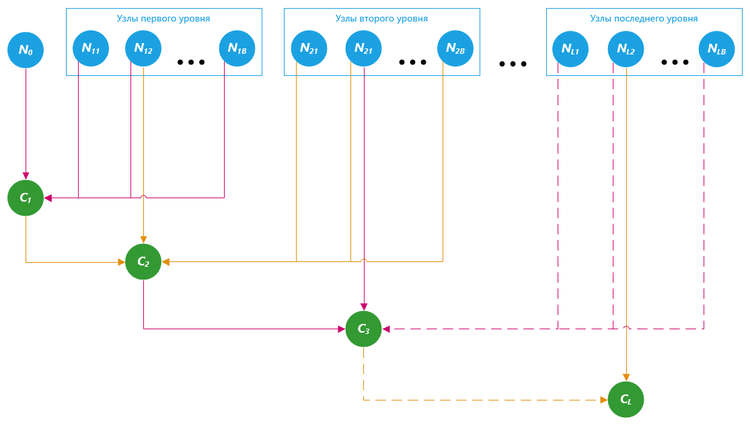
| + | [[file:Cobweb-flow-2.png|thumb|center|750px|Рис. 1 Информационный граф алгоритма COBWEB]] | ||
| − | + | <math>N_0</math> — корневой узел | |
| − | + | <math>N_{11}, N_{12}, ..., N_{1L}</math> — узлы первого уровня | |
| − | |||
| − | + | <math>N_{21}, N_{22}, ..., N_{2L}</math> — узлы второго уровня | |
| − | + | <math>N_{B1}, N_{B2}, ..., N_{BL}</math> — узлы последнего уровня | |
| − | + | <math>C_1, C_2, ..., C_L</math> — шаги спуска по дереву | |
| − | + | Для выполнения каждой итерации алгоритма (добавления очередного элемента в дерево классификации) необходимо иметь доступ по всему текущему состоянию дерева классификации. | |
| − | + | ||
| + | Однако, внутри шага алгоритма зависимость по данным отсутствует. Возможно произвести расчет функции полезности для каждого кластера независимо и в конце сравнить их значения. | ||
| − | == | + | == Ресурс параллелизма == |
| − | |||
| − | + | Основной вычислительной нагрузкой алгоритма является вычисление функции полезности для категорий. Эта часть алгоритма поддается наиболее простому распараллеливанию. Существует два пути к получению параллельной версии исходного алгоритма: | |
| − | + | * распараллеливание процесса вычисления совокупности функций полезности | |
| + | * распараллеливание вычисления каждой конкретной функции полезности | ||
| − | + | Оба данных подхода к распараллеливанию могут быть использованы вместе. | |
| − | + | * При неограниченном ресурсе параллелизма, вычисление функции полезности может быть произведено за <math>O(log(BAV))</math> через независимое вычисление каждой её составной части (за <math>O(1)</math>) и последующую их параллельную редукцию за <math>O(log(q))</math>, где <math>q=BAV</math> — количество составных частей функции полезности. | |
| + | * Вычисление совокупности функций полезности (которых <math>O(B)</math>) также может быть распараллелено c последующей параллельной редукцией за <math>O(log(B))</math> и итоговой параллельной сложностью <math>O(log(BAV)+log(B))=log(BAV))</math> (при неограниченном ресурсе параллелизма). | ||
| + | * Продвижение объектов по дереву может не может быть распараллелено, поскольку входные данные для каждой очередной итерации зависят от результата выполнения предыдущей. Всего за время работы алгоритма выполняется <math>O(N*logN)</math> операций продвижения по дереву. | ||
| − | + | Таким образом, итоговая параллельная сложность алгоритма равна <math>N*logN*log(BAV)</math>. | |
| − | + | == Входные и выходные данные алгоритма == | |
| + | На вход алгоритм принимает множество объектов, характеризуемых набором свойств. В свою очередь, каждое свойство может принимать какое-либо значение из множества допустимых значений. Оценка объема входных данных составляет <math>O(N*A)</math>. | ||
| − | + | Результатом работы алгоритма является построенное дерево классификации, листья которого представляют собой различные классы объектов и содержат сами объекты принадлежащие данному классу. Оценка объема выходных данных составляет <math>O(N*logN)</math>. | |
| − | + | == Свойства алгоритма == | |
| − | + | Этот алгоритм достаточно эффективен и выполняет кластеризацию на разумное число классов. Поскольку в нем используется вероятностное представление принадлежности, получаемые категории являются гибкими и робастными. Кроме того, в нем проявляется эффект категорий базового уровня, поддерживается прототипирование и учитывается степень принадлежности. Он основан не на классической логике, а, подобно методам теории нечетких множеств, учитывает "неопределенность" категоризации как необходимый компонент обучения и рассуждений в гибкой и интеллектуальной манере. | |
| − | + | Оценка вычислительной мощности алгоритма составляет <math>O(N * B * V * (A + logN))</math>. | |
= ЧАСТЬ. Программная реализация алгоритма = | = ЧАСТЬ. Программная реализация алгоритма = | ||
| Строка 129: | Строка 162: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | |||
| + | Исследование масштабируемости параллельной реализации алгоритма COBWEB проводилось на компьютере с процессором Intel(R) Core(TM) i7-5960X @ 4.30GHz, который поддерживает до 12ти потоков при наличии 6 физических ядер. Была взята реализация алгоритма COBWEB на Python из библиотки Concept Formation<ref name="gh_cf" /> и распараллелена с использованием средств Python multiprocessing<ref>https://docs.python.org/3.5/library/multiprocessing.html — библиотека multiprocessing для распараллеливания программ на Python</ref>. | ||
| + | |||
| + | Для исследования масштабируемости проводилось множество запусков программы с разным количеством объектов для кластеризации <math>N</math>, а также с различным числом процессоров. Фиксировались время работы и количество произведенных итераций алгоритма. | ||
| + | |||
| + | Параметры запусков для экспериментальной оценки: | ||
| + | * Количество объектов для кластеризации <math>N</math>: 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000 | ||
| + | * Количество процессоров <math>p</math>: 1, 2, 3, 4, 5, 6 | ||
| + | * Версия Python: 3.5 | ||
| + | |||
| + | Данные выбирались из стандартной библиотеки тестовых данных Библиоткеи Concept Formation (mushrooms). | ||
| + | |||
| + | Для заданной конфигурации эксперимента и полученным результатам [[Глоссарий#Производительность|производительность]] и эффективность реализации расчитывались по формулам: | ||
| + | |||
| + | <math>Perf = \frac{N_{op}}{t}\ \ (FLOPS),</math>, | ||
| + | где <math>N_{op}</math> — точное число операций с плавающей точкой (операции с памятью, а также целочисленные операции не учитывались), вычисленное в соответствие с разделом [[#Последовательная сложность алгоритма| "Последовательная сложность алгоритма"]]; | ||
| + | |||
| + | <math>Efficiency = \frac{100 * Performance}{Perf_{Peak}^{p}}\ \ (%),</math>, | ||
| + | где <math>Perf_{Peak}^{p}</math> – пиковая производительность суперкомпьютера при <math>p</math> процессорах, вычисленная согласно спецификациям Intel<sup>®</sup> Core i7<sup>®</sup> X5960<ref>"http://ark.intel.com/ru/products/82930/Intel-Core-i7-5960X-Processor-Extreme-Edition-20M-Cache-up-to-3_50-GHz"</ref>. | ||
| + | |||
| + | Графики зависимости производительности и эффективности параллельной реализации COBWEB от числа векторов для кластеризации (<math>N</math>) и числа процессоров (<math>p</math>) представлены ниже. | ||
| + | |||
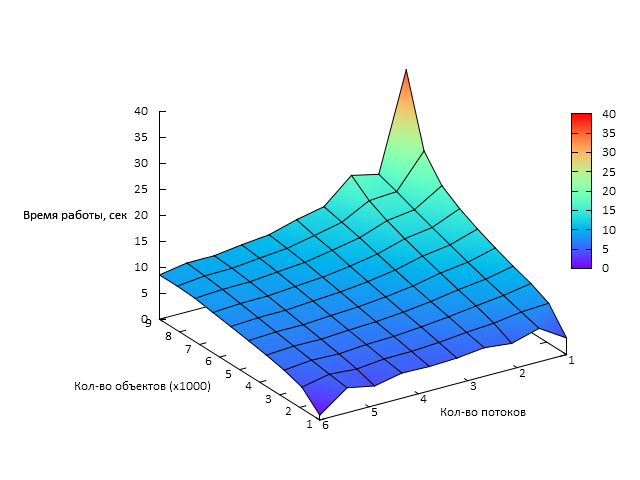
| + | [[file:Cobwebtime.png|thumb|center|640px|Рис. 2 Время работы алгоритма COBWEB в зависимости от числа процессов и размера задачи]] | ||
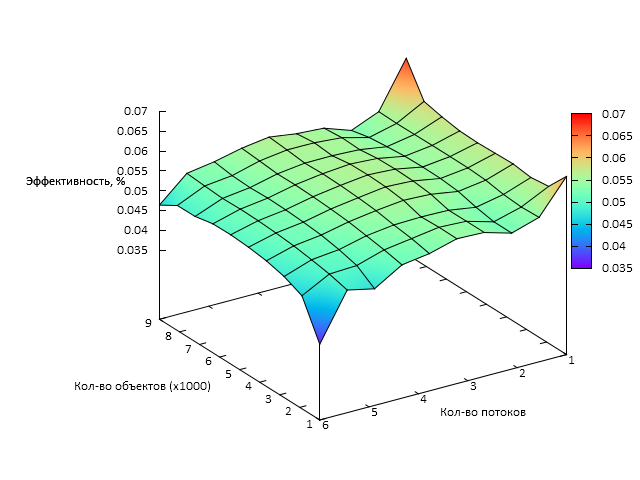
| + | [[file:Cobwebeff.png|thumb|center|640px|Рис. 3 Эффективность алгоритма COBWEB в зависимости от числа процессов и размера задачи]] | ||
| + | |||
| + | Таким образом можно сделать вывод о том, что данная реализация обладает слабой масштабируемостью. Во многом это связано с высокими накладными расходами на параллелизм в среде исполнения Python. | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 135: | Строка 194: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| + | |||
| + | Существуют следующие реализации алгоритма COBWEB: | ||
| + | * [https://github.com/cmaclell/concept_formation/ Concept Formation]<ref name="gh_cf">https://github.com/cmaclell/concept_formation/ — библиотека, содержащая реализации алгоритмов COBWEB и COBWEB/3 для языка Python</ref> библиотека, содержащая реализации алгоритмов COBWEB и COBWEB/3 для языка Python. | ||
| + | * [http://www.cs.waikato.ac.nz/~ml/weka Weka]<ref>http://www.cs.waikato.ac.nz/~ml/weka — библиотека и инструмент для анализа данных на языке Java</ref> библиотека и инструмент для анализа данных на языке Java. | ||
| + | * [http://java-ml.sourceforge.net/ Java-ML] <ref>http://java-ml.sourceforge.net/ — библиотека машинного обучения на языке Java</ref> библиотека машинного обучения на языке Java. | ||
| + | |||
| + | Так как существуют алгоритмы кластеризации, обладающие лучшими свойствами, алгоритм COBWEB практически не применяется и параллельных реализаций этого алгоритма нет. | ||
= Литература = | = Литература = | ||
| + | <references> | ||
| + | <ref name="wiki">https://en.wikipedia.org/wiki/Cobweb_(clustering) — описание алгоритма на Википедии (Eng)</ref> | ||
| + | <ref name="habr">https://habrahabr.ru/post/164417/ — сравнение алгоритма COBWEB с другими алгоритмами кластеризации</ref> | ||
| + | <ref name="shit">http://bourabai.ru/tpoi/analysis6.htm — подробное описание алгоритма COBWEB</ref> | ||
| + | <ref name="paper">http://www.cl.cam.ac.uk/~av308/cobweb.pdf — статья, в которой алгоритм COBWEB был впервые представлем</ref> | ||
| + | </references> | ||
Текущая версия на 16:13, 19 декабря 2016
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Dexter и ASA. |
| Алгоритм концептуальной кластеризации COBWEB | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(N*logN*B^{2}AV)[/math] |
| Параллельный алгоритм | |
| Параллельная сложность | [math]O(N*logN*log(BAV))[/math] |
Автор статьи: Артем Казаков (группа 624)
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Алгоритм COBWEB[1][2] — классический метод инкрементальной концептуальной кластеризации. Он создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт (концепт — описание группы объектов через определенный набор пар аттрибут-значение) и содержит вероятностное описание этого концепта, которое включает в себя вероятность принадлежности концепта к данному узлу.[3]
Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории — прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. Чтобы встроить новый объект в дерево классификации, алгоритм COBWEB итеративно проходит всё дерево в поисках «лучшего» узла, к которому отнести этот объект. Выбор узла осуществляется на основе помещения объекта в каждый узел и вычисления полезности категории получившегося среза. Также вычисляется полезность категории для случая, когда объект относится к вновь создаваемому узлу. В итоге объект относится к тому узлу, для которого полезность категории наибольшая.
Однако COBWEB имеет ряд ограничений. Во-первых, он предполагает, что распределения вероятностей значений различных атрибутов статистически независимы друг от друга. Однако это предположение не всегда верно, потому как часто между значениями атрибутов существует корреляция. Во-вторых, вероятностное представление кластеров делает очень сложным их обновление, особенно в том случае, когда атрибуты имеют большое число возможных значений. Это вызвано тем, что сложность алгоритма зависит не только от количества атрибутов, но и от количества их возможных значений.
1.2 Математическое описание алгоритма
Обозначим:
- [math]\{ A_{1}, A_{2}, ... \}[/math] — множество свойств кластеризуемых объектов
- [math]\{ u_{1j}, u_{2j}, ... \}[/math] — возможнные значения свойства [math]A_{j}[/math]
- [math]\{ C_{1}, C_{2}, ... \}[/math] — множество категорий
[math]P(A_j = u_{ij} | C_k)[/math] — это условная вероятность, с которой свойство [math]A_{j}[/math], принимает значение [math]u_{ij}[/math], если объект относится к категории [math]C_{k}[/math]. Для каждой категории в иерархии определены вероятности вхождения всех значений каждого свойства. При предъявлении нового экземпляра система COBWEB оценивает качество отнесения этого примера к существующей категории и модификации иерархии категорий в соответствии с новым представителем. Критерием оценки качества классификации является полезность категории (category utility).
Критерий полезности категории максимизирует вероятность того, что два объекта, отнесенные к одной категории, имеют одинаковые значения свойств и значения свойств для объектов из различных категорий отличаются. Полезность категории определяется формулой
[math]CU = \sum_{k} \sum_{i} \sum_{j} P(A_j = u_{ij}|C_k) P(C_k|A_j = u_{ij}) P(A_j = u_{ij})[/math][4]
Значения суммируются по всем категориям [math]C_k[/math], всем свойствам [math]A_j[/math] и всем значениям свойств [math]u_{ij}[/math]. Значение [math]P(A_j = u_{ij} | C_k)[/math] называется предсказуемостью (predictability). Это вероятность того, что объект, для которого свойство [math]A_j[/math] принимает значение [math]u_{ij}[/math], относится к категории [math]C_k[/math]. Чем выше это значение, тем вероятнее, что свойства двух объектов, отнесенных к одной категории, имеют одинаковые значения. Величина [math]P(C_k | A = u_{ij})[/math] называется предиктивностью (predictiveness). Это вероятность того, что для объектов из категории [math]C_k[/math] свойство [math]A_j[/math] принимает значение [math]u_{ij}[/math]. Чем больше эта величина, тем менее вероятно, что для объектов, не относящихся к данной категории, это свойство будет принимать указанное значение. Значение [math]P(A = u_{ij})[/math] — это весовой коэффициент, усиливающий влияние наиболее распространенных свойств. Благодаря совместному учету этих значений высокая полезность категории означает высокую вероятность того, что объекты из одной категории обладают одинаковыми свойствами, и низкую вероятность наличия этих свойств у объектов из других категорий.
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на вычисление полезности категории.
Обозначим:
- [math]B[/math] — среднее число потомков узлов в дереве классификации
- [math]N[/math] — число объектов для классификации
- [math]A[/math] — числа свойств у классифицируемых объектов
- [math]V[/math] — среднее число значений, которые могут принимать свойства
На каждом шаге алгоритма (всего [math]N[/math] производится спуск по дереву ([math]O(log_{B}N)[/math]). На каждой итерации спуска производится [math]O(B)[/math] вычислений полезности категории [math]CU[/math], вычисление каждой из которых имеет сложность [math]O(BAV)[/math].
Перемножив сложности выше получам сложность из п. 1.6., что подтверждает, что основная часть вычислительных операций приходится именно на вычисление полезностей категорий.
1.4 Макроструктура алгоритма
В алгоритме COBWEB реализован метод поиска экстремума в пространстве возможных кластеров с использованием критерия полезности категорий для оценки и выбора возможных способов категоризации.
- Сначала вводится единственная категория, свойства которой совпадают со свойствами первого экземпляра.
- Для каждого последующего экземпляра алгоритм начинает свою работу с корневой категории и движется далее по дереву.
- На каждом уровне выполняется оценка эффективности категоризации на основе полезности категории. При этом оцениваются результаты следующих операций:
- Отнесение экземпляра к наилучшей из существующих категорий.
- Добавление новой категории, содержащей единственный экземпляр.
- Слияние двух существующих категорий в одну новую с добавлением в нее этого экземпляра.
- Разбиение существующей категории на две и отнесение экземпляра к лучшей из вновь созданных категорий.
- Для слияния двух узлов создается новый узел, для которого существующие узлы становятся дочерними. На основе значений вероятностей дочерних узлов вычисляются вероятности для нового узла. При разбиении один узел заменяется двумя дочерними.
1.5 Схема реализации последовательного алгоритма
Алгоритм повторяется для каждого нового объекта. В данном алгоритме происходит спуск по дереву и на каждом шаге спуска выбирается одно из действий описанных в п. 1.4.
cobweb(Node, Instance)
Begin
if узел Node - это лист, then
begin
создать два дочерних узла L1 и L2 для узла Node;
задать для узла L1 те же вероятности, что и для узла Node;
инициализировать вероятности для узла L2 соответствующими значениями объекта Instance;
добавить Instance к Node, обновив вероятности для узла Node ;
end
else
begin
добавить Instance к Node, обновив вероятности для узла Node;
для каждого дочернего узла С узла Node вычислить полезность категории при отнесении экземпляра Instance к категории С;
пусть S1 - значение полезности для наилучшей классификации C1;
пусть S2 - значение для второй наилучшей классификации C2;
пусть S3 - значение полезности для отнесения экземпляра к новой категории;
пусть S4 - значение для слияния C1 и C2 в одну категорию;
пусть S5 - значение для разделения C1 (замены дочерними категориями);
end
if S1 - максимальное значение CU, then
cobweb(C1, Instance) %отнести экземпляр к C1
else
if S3 - максимальное значение CU, then
инициализировать вероятности для новой категории Cm значениями Instance
else
if S4 - максимальное значение CU, then
begin
пусть Cm - результат слияния C1 и C2;
cobweb(Cm, Instance);
end
else
if S5 - максимальное значение CU, then
begin
разделить C1; % Cm - новая категория
cobweb(Cm, Instance)
end;
end
1.6 Последовательная сложность алгоритма
Последовательная сложность алгоритма равна [math]O(N*log_{B}N*B^{2}AV)[/math]
где:
- [math]B[/math] — среднее число потомков узлов в дереве классификации
- [math]N[/math] — число объектов для классификации
- [math]A[/math] — числа свойств у классифицируемых объектов
- [math]V[/math] — среднее число значений, которые могут принимать свойства
Обоснование сложности приводится в п. 1.3.
1.7 Информационный граф
[math]N_0[/math] — корневой узел
[math]N_{11}, N_{12}, ..., N_{1L}[/math] — узлы первого уровня
[math]N_{21}, N_{22}, ..., N_{2L}[/math] — узлы второго уровня
[math]N_{B1}, N_{B2}, ..., N_{BL}[/math] — узлы последнего уровня
[math]C_1, C_2, ..., C_L[/math] — шаги спуска по дереву
Для выполнения каждой итерации алгоритма (добавления очередного элемента в дерево классификации) необходимо иметь доступ по всему текущему состоянию дерева классификации.
Однако, внутри шага алгоритма зависимость по данным отсутствует. Возможно произвести расчет функции полезности для каждого кластера независимо и в конце сравнить их значения.
1.8 Ресурс параллелизма
Основной вычислительной нагрузкой алгоритма является вычисление функции полезности для категорий. Эта часть алгоритма поддается наиболее простому распараллеливанию. Существует два пути к получению параллельной версии исходного алгоритма:
- распараллеливание процесса вычисления совокупности функций полезности
- распараллеливание вычисления каждой конкретной функции полезности
Оба данных подхода к распараллеливанию могут быть использованы вместе.
- При неограниченном ресурсе параллелизма, вычисление функции полезности может быть произведено за [math]O(log(BAV))[/math] через независимое вычисление каждой её составной части (за [math]O(1)[/math]) и последующую их параллельную редукцию за [math]O(log(q))[/math], где [math]q=BAV[/math] — количество составных частей функции полезности.
- Вычисление совокупности функций полезности (которых [math]O(B)[/math]) также может быть распараллелено c последующей параллельной редукцией за [math]O(log(B))[/math] и итоговой параллельной сложностью [math]O(log(BAV)+log(B))=log(BAV))[/math] (при неограниченном ресурсе параллелизма).
- Продвижение объектов по дереву может не может быть распараллелено, поскольку входные данные для каждой очередной итерации зависят от результата выполнения предыдущей. Всего за время работы алгоритма выполняется [math]O(N*logN)[/math] операций продвижения по дереву.
Таким образом, итоговая параллельная сложность алгоритма равна [math]N*logN*log(BAV)[/math].
1.9 Входные и выходные данные алгоритма
На вход алгоритм принимает множество объектов, характеризуемых набором свойств. В свою очередь, каждое свойство может принимать какое-либо значение из множества допустимых значений. Оценка объема входных данных составляет [math]O(N*A)[/math].
Результатом работы алгоритма является построенное дерево классификации, листья которого представляют собой различные классы объектов и содержат сами объекты принадлежащие данному классу. Оценка объема выходных данных составляет [math]O(N*logN)[/math].
1.10 Свойства алгоритма
Этот алгоритм достаточно эффективен и выполняет кластеризацию на разумное число классов. Поскольку в нем используется вероятностное представление принадлежности, получаемые категории являются гибкими и робастными. Кроме того, в нем проявляется эффект категорий базового уровня, поддерживается прототипирование и учитывается степень принадлежности. Он основан не на классической логике, а, подобно методам теории нечетких множеств, учитывает "неопределенность" категоризации как необходимый компонент обучения и рассуждений в гибкой и интеллектуальной манере.
Оценка вычислительной мощности алгоритма составляет [math]O(N * B * V * (A + logN))[/math].
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование масштабируемости параллельной реализации алгоритма COBWEB проводилось на компьютере с процессором Intel(R) Core(TM) i7-5960X @ 4.30GHz, который поддерживает до 12ти потоков при наличии 6 физических ядер. Была взята реализация алгоритма COBWEB на Python из библиотки Concept Formation[5] и распараллелена с использованием средств Python multiprocessing[6].
Для исследования масштабируемости проводилось множество запусков программы с разным количеством объектов для кластеризации [math]N[/math], а также с различным числом процессоров. Фиксировались время работы и количество произведенных итераций алгоритма.
Параметры запусков для экспериментальной оценки:
- Количество объектов для кластеризации [math]N[/math]: 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000
- Количество процессоров [math]p[/math]: 1, 2, 3, 4, 5, 6
- Версия Python: 3.5
Данные выбирались из стандартной библиотеки тестовых данных Библиоткеи Concept Formation (mushrooms).
Для заданной конфигурации эксперимента и полученным результатам производительность и эффективность реализации расчитывались по формулам:
[math]Perf = \frac{N_{op}}{t}\ \ (FLOPS),[/math], где [math]N_{op}[/math] — точное число операций с плавающей точкой (операции с памятью, а также целочисленные операции не учитывались), вычисленное в соответствие с разделом "Последовательная сложность алгоритма";
[math]Efficiency = \frac{100 * Performance}{Perf_{Peak}^{p}}\ \ (%),[/math], где [math]Perf_{Peak}^{p}[/math] – пиковая производительность суперкомпьютера при [math]p[/math] процессорах, вычисленная согласно спецификациям Intel® Core i7® X5960[7].
Графики зависимости производительности и эффективности параллельной реализации COBWEB от числа векторов для кластеризации ([math]N[/math]) и числа процессоров ([math]p[/math]) представлены ниже.
Таким образом можно сделать вывод о том, что данная реализация обладает слабой масштабируемостью. Во многом это связано с высокими накладными расходами на параллелизм в среде исполнения Python.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существуют следующие реализации алгоритма COBWEB:
- Concept Formation[5] библиотека, содержащая реализации алгоритмов COBWEB и COBWEB/3 для языка Python.
- Weka[8] библиотека и инструмент для анализа данных на языке Java.
- Java-ML [9] библиотека машинного обучения на языке Java.
Так как существуют алгоритмы кластеризации, обладающие лучшими свойствами, алгоритм COBWEB практически не применяется и параллельных реализаций этого алгоритма нет.
3 Литература
- ↑ https://en.wikipedia.org/wiki/Cobweb_(clustering) — описание алгоритма на Википедии (Eng)
- ↑ http://www.cl.cam.ac.uk/~av308/cobweb.pdf — статья, в которой алгоритм COBWEB был впервые представлем
- ↑ https://habrahabr.ru/post/164417/ — сравнение алгоритма COBWEB с другими алгоритмами кластеризации
- ↑ http://bourabai.ru/tpoi/analysis6.htm — подробное описание алгоритма COBWEB
- ↑ Перейти обратно: 5,0 5,1 https://github.com/cmaclell/concept_formation/ — библиотека, содержащая реализации алгоритмов COBWEB и COBWEB/3 для языка Python
- ↑ https://docs.python.org/3.5/library/multiprocessing.html — библиотека multiprocessing для распараллеливания программ на Python
- ↑ "http://ark.intel.com/ru/products/82930/Intel-Core-i7-5960X-Processor-Extreme-Edition-20M-Cache-up-to-3_50-GHz"
- ↑ http://www.cs.waikato.ac.nz/~ml/weka — библиотека и инструмент для анализа данных на языке Java
- ↑ http://java-ml.sourceforge.net/ — библиотека машинного обучения на языке Java