Участник:MelLain/ЕМ-алгоритм (Тематическое моделирование): различия между версиями
MelLain (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | {{Assignment|Algoman}} | + | {{Assignment|Algoman|Dexter}} |
| + | |||
Статью подготовили: | Статью подготовили: | ||
| Строка 113: | Строка 114: | ||
2. Внешняя итерация по коллекции i = 1 ... num_outer_iter: | 2. Внешняя итерация по коллекции i = 1 ... num_outer_iter: | ||
| − | 3. | + | 3. n_wt^i := 0, n_t^i := 0 для всех w из W и t из T; |
| − | 4. | + | 4. Цикл по документам d из D: |
| − | 5. | + | 5. Инициализировать вектор theta_d^0 для всех t из T и Z_w^0, для всех w из d; |
| − | 6. | + | 6. Внутренняя итерация по документу j = 1 ... num_inner_iter: |
| − | 7. | + | 7. Z_w^j := сумме по всем t из T (phi_wt^(i-1) * theta_td^(j-1)), для всех w из d; |
| − | 8. | + | 8. theta_td^j := (1 / n_d) * на сумму по w из d (n_dw * phi_wt^(i-1) * theta_td^(j-1) / Z_w^j), для всех t из T; |
| − | 9. | + | 9. Увеличить n_wt^i и n_t^i на (n_dw * phi_wt^(i-1) * theta_td / Z_w), для всех w из W и t из T; |
| − | 10. | + | 10. phi_wt^i := (n_wt^i / n_t^i), для всех w из W и t из T |
Здесь Z_w - это сумма всех p(t| d, w) для данного документа, нормировочная константа. | Здесь Z_w - это сумма всех p(t| d, w) для данного документа, нормировочная константа. | ||
| Строка 172: | Строка 173: | ||
Внутри алгоритма используются элементарные операции | Внутри алгоритма используются элементарные операции | ||
* Умножения матрицы на вектор <math>M \cdot V</math>, | * Умножения матрицы на вектор <math>M \cdot V</math>, | ||
| − | * Поэлементного умножения вектора на вектор <math> | + | * Поэлементного умножения вектора на вектор <math>U. \cdot V</math>, |
| − | * Поэлементного деления вектора на вектор <math>U. | + | * Поэлементного деления вектора на вектор <math>U. / V</math>. |
Данные операции были рассмотрены в [https://algowiki-project.org/ru/%D0%A1%D1%83%D0%BC%D0%BC%D0%B0_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B0_%D0%B8_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D1%8B_%D0%BD%D0%B0_%D0%B4%D1%80%D1%83%D0%B3%D0%BE%D0%B9_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80,_%D0%B2%D0%B5%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F_%D0%B2%D0%B5%D1%80%D1%81%D0%B8%D1%8F,_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82,_%D0%BF%D0%BB%D0%BE%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0 соответствующей статье], поэтому не будем останавливаться отдельно на каждой из них. | Данные операции были рассмотрены в [https://algowiki-project.org/ru/%D0%A1%D1%83%D0%BC%D0%BC%D0%B0_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B0_%D0%B8_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%B5%D0%B4%D0%B5%D0%BD%D0%B8%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D1%8B_%D0%BD%D0%B0_%D0%B4%D1%80%D1%83%D0%B3%D0%BE%D0%B9_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80,_%D0%B2%D0%B5%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F_%D0%B2%D0%B5%D1%80%D1%81%D0%B8%D1%8F,_%D0%BF%D0%BE%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82,_%D0%BF%D0%BB%D0%BE%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0 соответствующей статье], поэтому не будем останавливаться отдельно на каждой из них. | ||
Текущая версия на 16:20, 19 декабря 2016
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Dexter и Algoman. |
Статью подготовили:
- Мурат Апишев (реализация кода, описание теоретической части и деталей реализации);
- Андрей Заночкин (реализация кода, информационный граф, оценки сложности и экспериментальная часть).
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Тематическое моделирование[1][2] - одно из направлений статистического анализа текстовых коллекций в машинном обучении. В литературе описываются многочисленные разновидности моделей, а также методов их обучения. В данной статье будет рассмотрена тематическая модель вероятностного латентного семантического анализа[3] (PLSA), и процесс её обучения с помощью параллельного ЕМ-алгоритма.
Существует множество разновидностей ЕМ-алгоритмов, ориентированных на учёт тех или иные аспектов решаемой задачи. Наиболее простым вариантом является т.н. оффлайновый алгоритм, непригодный для работы с большими текстовыми данными в силу значительных требований к потребляемой оперативной памяти. Существует ряд модернизаций этого алгоритма, позволяющих избавить его от ряда недостатков. Наилучшей из них является онлайновый вариант алгоритма. Тем не менее, в силу относительно высокой сложности его эффективной параллельной реализации, в данной статье будет рассматриваться гибридный вариант алгоритма, избавленный от большинства недостатков оффлайнового, но имеющий меньшую скорость сходимости, чем онлайновый.
1.2 Математическое описание алгоритма
1.2.1 Математическое описание модели
В большинстве тематических моделей коллекция текстов рассматривается в виде "мешка слов", т.е. модель учитывает только статистическую встречаемость слов в документах и никак не использует информацию об их взаимном расположении внутри документа.
Вероятностная модель PLSA имеет следующий вид:
- [math] \begin{align} F \approx \Phi \times \Theta \end{align} [/math]
Здесь [math]F[/math] - это матрица исходных данных размера [math]|W| \times |D|[/math], где [math]D[/math] - это множество документов, а [math]W[/math] - словарь коллекции, т.е. множество всех уникальных слов, встретившихся в документах.
[math]\Phi[/math] - это матрица параметров модели размера [math]|W| \times |T|[/math], где [math]T[/math] - это множество тем, которые мы хотим извлечь из коллекции. Под темой в бытовом смысле смысле понимается набор слов, характеризующих её. Формально говоря, тема - это вероятностное распределение на множестве слов [math]W[/math], поэтому матрица [math]\Phi[/math] является стохастической, т.е. столбцы её неотрицательны и суммируются в единицу.
[math]\Theta[/math] - матрица результатов кластеризации обучающей коллекции по полученным темам размера [math]|T| \times |D|[/math], в ней столбцы также являются вероятностными распределениями, на этот раз документов на множестве тем.
Фактически, PLSA есть ни что иное, как задача приближённого стохастического матричного разложения, в ходе которой производится мягкая бикластеризация данных (мягкая - потому что объекты распределяются по классам не строго, а с некоторой вероятностью, би - потому что производится одновременная кластрезация слов по темам, и тем - по документам). Поставленную задачу можно решать методом максимального правдоподобия, с помощью ЕМ-алгоритма.
В данной статье будут расматриваться только плотные матрицы (хотя при определённых условиях можно эффективно использовать разреженные).
1.2.2 Математическое описание ЕМ-алгоритма
Задача максимизации логарифма правдоподобия для описанной модели имеет следующий вид:
- [math] \begin{align} \mathcal{L}(\Phi, \Theta) = \sum_{d \in D}\sum_{w \in d} n_{dw} \,\mathrm{ln}(\sum_{t \in T} \phi_{wt} \theta_{td}) \rightarrow \underset{\Phi, \Theta}{\mathrm{max}} \end{align} [/math]
- [math] \begin{align} \sum_{w \in W} \phi_{wt} = 1, \, \forall t \in T, \quad \phi_{wt} \ge 0; \end{align} [/math]
- [math] \begin{align} \sum_{t \in T} \theta_{td} = 1, \, \forall d \in D, \quad \theta_{td} \ge 0. \end{align} [/math]
Прямая оптимизация логарифма правдоподобия - очень сложная задача, поэтому её решают приближённо с помощью метода простых итераций, в котором чередуются два шага: E (expectation) и M (maximization). Перед первой итерацией выбираются начальные приближения параметров [math]\Phi[/math] и [math]\Theta[/math].
На Е-шаге по текущим значениям параметров с помощью формулы Байеса вычисляются вспомогательные переменные - условные вероятности [math]p(t\, | \,d, \,w)[/math] для всех тем [math]t \in T[/math], для каждого термина [math]w \in d[/math] для каждого документа [math]d \in D[/math]:
- [math] \begin{align} p(t\, | \,d, \,w ) = \cfrac{\phi_{wt}\theta_{td}}{\sum_{s \in T}\phi_{ws}\theta_{sd}} \end{align} [/math]
На М-шаге, наоброт, по условным вероятностям [math]p(t\, | \,d, \,w)[/math] вычисляется новое приближение параметров [math]\phi_{wt}[/math], [math]\theta_{td}[/math]:
- [math] \begin{align} \phi_{wt} = \cfrac{\hat n_{wt}}{\hat n_t}, \quad \hat n_t = \sum_{w \in W} \hat n_{wt}, \quad \hat n_{wt} = \sum_{d \in D} n_{dw} p(t\, | \,d, \,w ) \end{align} [/math]
- [math] \begin{align} \theta_{td} = \cfrac{\hat n_{dt}}{\hat n_d}, \quad \hat n_d = \sum_{t \in T} \hat n_{dt}, \quad \hat n_{dt} = \sum_{w \in d} n_{dw} p(t\, | \,d, \,w ) \end{align} [/math]
Под [math]n_{dw}[/math] здесь понимается абсолютная частота встречаемости слова [math]w[/math] в документе [math]d[/math].
Строгое обоснование данных формул можно получить с помощью теоремы Куна-Таккера.
1.2.3 Модернизации алгоритма
Как уже было сказано, и как видно из описания выше, данный алгоритм сложно применять на практике в чистом виде из-за необходимости хранения трёхмерной матрицы [math]p(t\, | \,d, \,w)[/math] и двумерной матрицы [math]\Theta[/math], размеры которых зависят от количества обрабатываемых и данных, которых может быть очень много.
Для борьбы с описанной проблемой можно производить вычисления более рационально, отказавшись от хранения обеих матриц и вычисляя необходимы значения на лету. При наличии обученной модели [math]\Phi[/math] получить векторы распределений [math]\theta_d[/math] (если в этом есть необходимость) можно, произведя одну итерацию алгоритма, в ходе которой сама модель обновляться не будет.
В этом варианте алгоритма вычисление [math]\theta_d[/math] будет перенесено с М-шага на Е-шаг, и для каждого нового документа этот вектор будет инициализирован равномерным распределением. Для ускорения скорости сходимости можно производить итерации "пересчёт [math]p(t\, | \,d, \,w)[/math]" - "обновление [math]\theta_d[/math]" многократно в течении обработки одного документа.
В дальнейшем подобные итерации будем называть "внутренними", полный же однократный проход по всей коллекции будем называть итерацией "внешней".
1.3 Вычислительное ядро алгоритма
Наиболее вычислительно затратной операцией в данном алгоритме является Е-шаг, в ходе которого рассчитываются вспомогательные переменные и векторы [math]\theta_d[/math]. С введением внутренних итераций нагрузка на Е-шаг только увеличивается.
1.4 Макроструктура алгоритма
В целом, высокоуровневое описание ЕМ-алгоритма состоит из самих Е-шага и М-шага, что можно видеть на нижеприведённом листинге.
1.5 Схема реализации последовательного алгоритма
Приведём здесь листинг описываемого алгоритма:
1. Инициализировать phi_wt^0 для всех w из W, t из T;
2. Внешняя итерация по коллекции i = 1 ... num_outer_iter:
3. n_wt^i := 0, n_t^i := 0 для всех w из W и t из T;
4. Цикл по документам d из D:
5. Инициализировать вектор theta_d^0 для всех t из T и Z_w^0, для всех w из d;
6. Внутренняя итерация по документу j = 1 ... num_inner_iter:
7. Z_w^j := сумме по всем t из T (phi_wt^(i-1) * theta_td^(j-1)), для всех w из d;
8. theta_td^j := (1 / n_d) * на сумму по w из d (n_dw * phi_wt^(i-1) * theta_td^(j-1) / Z_w^j), для всех t из T;
9. Увеличить n_wt^i и n_t^i на (n_dw * phi_wt^(i-1) * theta_td / Z_w), для всех w из W и t из T;
10. phi_wt^i := (n_wt^i / n_t^i), для всех w из W и t из T
Здесь Z_w - это сумма всех p(t| d, w) для данного документа, нормировочная константа.1.6 Последовательная сложность алгоритма
Рассмотрим ЕМ-алгоритм с [math]num\_outer\_iter[/math] внешними итерациями и [math]num\_inner\_iter[/math] внутренними применительно к набору документов [math]D[/math] и слов [math]W[/math], классифицирующий коллекцию по темам [math]T[/math].
Так на каждой внутренней итерации производится
- умножений: [math]|W|\cdot|T| + 2|T|\cdot|D|[/math] ,
- делений : [math]|T|\cdot(|D| + 1)[/math],
- сложений: [math]|W|\cdot(|T|-1) + |T|\cdot(|D| - 1)[/math].
А значит на одной внешней итерации производится
- умножений: [math](|W|\cdot|T| + 2|T|\cdot|D|)\cdot num\_inner\_iter \cdot |D|[/math] ,
- делений : [math]|T|\cdot(|D| + 1)\cdot num\_inner\_iter \cdot |D| + |W|\cdot|T|[/math] ,
- сложений: [math]\Big(\big[|W|\cdot(|T|-1) + |T|\cdot(|D| - 1)\big]\cdot num\_inner\_iter + |W|\cdot|T|\Big)\cdot |D|[/math] .
Соответственно для всего алгоритма каждая из этих операций повторяется [math]num\_outer\_iter[/math] раз. Наиболее часто выполняется операция умножения, однако порядок величин одинаковый. Разница будет заметна лишь в том случае, когда [math]|D|[/math] имеет меньший порядок, чем [math]|W|[/math]. В этом случае делений будет значительно меньше, чем сложений и умножений.
По классификации по последовательной сложности ЕМ-алгоритм можно отнести к линейным по [math]num\_inner\_iter, num\_outer\_iter , |T|, |W|[/math], а попеременной [math]|D|[/math] - с квадратичной сложностью.
1.7 Информационный граф
Опишем граф алгоритма[4][5][6] как аналитически, так и в виде рисунка.
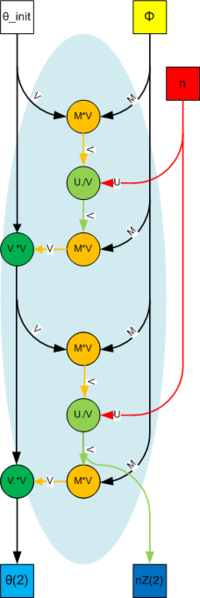
Первый граф описывает алгоритм внутреннего цикла.
В качестве входных параметров выступают
- вектор [math]\theta_{init} [/math], инициализированный значениями [math]1/|T|[/math], длиной [math]|T|[/math],
- матрица [math]\Phi[/math], размера [math]|W|\times |T|[/math],
- вектор [math]n[/math], длины [math]|W|[/math].
В качестве выходных параметров выступают
- вектор [math]\theta[/math], длиной [math]|T|[/math],
- вектор [math]nZ[/math], длиной [math]|W|[/math].
Внутри алгоритма используются элементарные операции
- Умножения матрицы на вектор [math]M \cdot V[/math],
- Поэлементного умножения вектора на вектор [math]U. \cdot V[/math],
- Поэлементного деления вектора на вектор [math]U. / V[/math].
Данные операции были рассмотрены в соответствующей статье, поэтому не будем останавливаться отдельно на каждой из них.
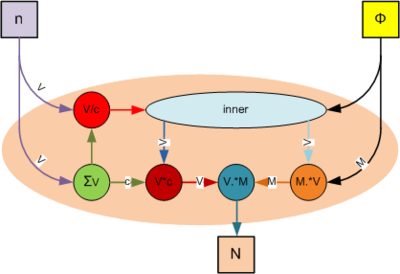
Второй граф описывает Е-шаг алгоритма при анализе отдельного документа.
В качестве входных параметров выступают
- матрица [math]\Phi[/math], размера [math]|W|\times |T|[/math],
- вектор [math]n[/math], длины [math]|W|[/math].
В качестве выходных параметров выступают
- матрица [math]N[/math], размера [math]|W|\times |T|[/math].
Внутри алгоритма используются элементарные операции
- Суммирования элементов вектора [math]\Sigma[/math],
- Поэлементного деления вектора на скаляр [math]V / c[/math],
- Поэлементного умножения вектора на скаляр [math]V \cdot c[/math],
- Умножения строк матрицы на элементы вектора [math]M. \cdot V[/math],
- Умножения столбцов матрицы на элементы вектора [math]V. \cdot M[/math].
А также используется операция [math]inner[/math], описанная на предыдущем шаге.
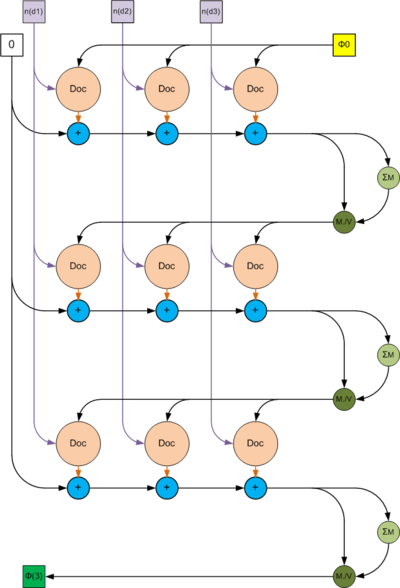
Третий граф описывает алгоритм внешнего цикла.
В качестве входных параметров выступают
- Нулевая матрица, размера [math]|W|\times |T|[/math],
- матрица [math]\Phi_0[/math], размера [math]|W|\times |T|[/math],
- Набор векторов [math]n(d_i)[/math], длины [math]|W|[/math], являющихся столбцами матрицы [math]n_{wd}[/math].
В качестве выходных параметров выступают
- вектор [math]\theta_{num\_outer\_iter}[/math], длиной [math]|T|[/math].
Внутри алгоритма используются элементарные операции
- Суммы двух матриц ,
- Суммы элементов столбцов матрицы [math]\Sigma M[/math],
- Деления столбцов матрицы на элементы вектора [math]M./ V[/math].
А также используется операция [math]Doc[/math], описанная на втором шаге.
1.8 Ресурс параллелизма алгоритма
Е-шаг представляет собой наиболее подходящее место в алгоритме для применения параллелизма. Во-первых, потому, что является наиболее ресурсоёмким этапом, во-вторых - потому что в нём производится итерирование по документам коллекции, при этом обработка каждого документа выполняется фактически независимо.
Параллелить также можно и М-шаг, но в данной статье это не будет рассматриваться за ненадобностью. В практических реализациях это делается крайне редко.
1.9 Входные и выходные данные алгоритма
Если рассматривать EM-алгоритм на прикладном уровне, то в качестве входных параметров выступает коллекция документов [math]D[/math], которая предварительно анализируется и порождает множество слов [math]W[/math]. Также к входным данным относится количество тем [math]T[/math]. Поскольку анализ документов и выделение слов являются отдельной задачей, то мы будем полагать, что на вход подаются оцифрованные данные в следующем виде:
Входные данные:
- матрица частот [math]n_{dw}[/math], отвечающая количеству слов [math]w[/math], встречающихся в документе [math]d[/math]. По определению элементы этой матрицы могут принимать лишь неотрицательные целые значения.
- пара параметров [math]num\_outer\_iter, num\_inner\_iter[/math] и количество тем [math]|T|[/math]. Эти величины могут быть только положительными целыми числами.
Объём входных данных:
- Матрица частот размером [math]|W|\times |D|[/math], а также три скалярные константы.
Выходные данные:
- Матрица модели [math]\Phi[/math], то есть распределений слов в полученных темах (если добавить кэширование матрицы [math]\Theta[/math], то можно сразу получить и её, хотя это скажется на объёме потребляемой памяти).
Объём выходных данных:
- [math]|W|\times|T| \big(+ |T|\times|D| \big)[/math].
1.10 Свойства алгоритма
С вычислительной точки зрения алгоритм является детерминированным, в силу фиксированного взаимного размещения данных в памяти. Масштабируемость параллельной реализации может зависеть от ряда факторов, которые будут рассмотрены далее.
С точки зрения результата работы алгоритм детерминированным не является, он неустойчив, имеет тенденцию к попаданию в локальные минимумы. Результат работы сильно зависит от начального приближения, которое, как правило, выбирается случайным образом.
Вычислительная мощность алгоритма равна отношению числа операций к суммарному объему входных и выходных данных. Она показывает, сколько операций приходится на единицу переданных данных.
Суммарное количество входных параметров можно читать равным [math]|W|\times|D| [/math]
Суммарное количество выходных параметров в точности равно [math]|W|\times|T| (+ |T|\times |D|) [/math]
Количество операций при больших значениях параметров [math]num\_outer\_iter[/math] и [math]num\_inner\_iter[/math] можно считать равным [math](2|W|\cdot|T| + 4|T|\cdot|D|)\cdot |D| \cdot num\_inner\_iter \cdot num\_outer\_iter[/math]
Итак вычислительная сложность алгоритма равна [math]\frac{(2|W|\cdot|T| + 4|T|\cdot|D|)\cdot |D|}{|W|\cdot|D| + |W|\cdot|T| (+ |T|\cdot |D|)} \cdot num\_inner\_iter \cdot num\_outer\_iter[/math]
Очевидно, что по параметрам итерации вычислительная сложность линейна. Более сложная зависимость наблюдается по параметрам количества тем, слов и документов. Наибольший интерес представляет зависимость сложности от количества документов, поскольку на практике именно этот параметр имеет больший порядок, нежели остальные значения. Так асимптотически алгоритм имеет линейную сложность по этому параметру. По остальным же параметрам вычислительная сложность ограничена некоторой константой, которая зависит от других параметров и может быть легко получена взятием предела выражения по соответствующим переменным.
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте (без внутренних итераций по [math]\theta_d[/math] и с хранением всех этих векторов) алгоритм без применения параллелизма и векторизации на языке Python выглядит следующим образом:
# Author: Murat Apishev (great-mel@yandex.ru)
def plsa_em(n_dw, num_topics, max_outer_iter, Phi_init, Theta_init):
num_tokens, num_docs = n_dw.shape
Phi = Phi_init if not Phi_init is None else init_matrix(num_tokens, num_topics)
Theta = Theta_init if not Theta_init is None else init_matrix(num_topics, num_docs)
for i in xrange(max_outer_iter):
time_start = time.time()
n_wt = np.zeros([num_tokens, num_topics]);
n_t = [0] * num_topics
Theta_new = np.array(Theta)
for d in xrange(num_docs):
Z_w = [0] * num_tokens
for w in xrange(num_tokens):
z_w = 0.0
for t in xrange(num_topics):
z_w += Phi[w, t] * Theta[t, d]
Z_w[w] = z_w
for t in xrange(num_topics):
value = 0.0
for w in xrange(num_tokens):
if Z_w[w] < EPS:
continue
value += n_dw[w, d] * Phi[w, t] * Theta[t, d] / Z_w[w]
denominator = np.sum(n_dw[:, d])
if denominator < EPS:
continue
Theta_new[t, d] = 1.0 / np.sum(n_dw[:, d]) * value
for w in xrange(num_tokens):
for t in xrange(num_topics):
if Z_w[w] < EPS:
continue
value = n_dw[w, d] * Phi[w, t] * Theta[t, d] / Z_w[w]
n_wt[w, t] += value
n_t[t] += value
Phi = n_wt / n_t
Theta = Theta_new
return Phi, Theta
2.2 Локальность данных и вычислений
В параллельной реализации присутствует локальность данных. Основным разделяемым ресурсом для потоков-обработчиков является матрицы [math]n_{wt}[/math] и [math]\Phi[/math]. Они хранятся в виде хэш-таблиц, где ключом является слово, а значением - вектор, длинной в число тем. В силу последовательного хранения данных вектором, производится эффективное итерирование в циклах по темам.
2.3 Возможные способы и особенности параллельной реализации алгоритма
Вне зависимости от того, каким образом производить параллельную/распределённую обработку коллекции, основным способом увеличения производительности является разделение обработки отдельных документов. Существующие архитектуры алгоритмов тематического моделирования (не только на основе описанного ЕМ-алгоритма) на MPI, Hadoop MapReduce, Spark, а также параллельные архитектуры на одиночных машинах, работают в рамках одной этой парадигмы.
Как уже было отмечено, в описанном алгоритме большая часть вычислений приходится на Е-шаг (в некоторых экспериментах он занимал более 99% времени работы). Поэтому именно он был выбран в качестве объекта для реализации параллелизма. Общую схему можно описать следующим образом. Вместо того, чтобы обрабатывать документы в цикле последовательно, можно делать это параллельно, поскольку для описанного алгоритма обработка разных документов являются независимыми операциями. Таким образом, входные данные, то есть документы, разбиваются на пакеты, в каждом из которых находится фиксированное количество документов, каждый пакет сохраняется на диск в виде отдельного файла, все файлы хранятся в одной директории, подаваемой на вход алгоритму.
Далее алгоритм перед началом очередной итерации прохода по коллекции просматривает рабочую директорию и сохраняет в специальную очередь имена файлов с документами. Перед началом каждой итерации производится создание нескольких параллельных потоков-обработчиков, каждый из которых занимается вычислением Е-шага. Для этого каждый обработчик, не занятый в текущий момент времени, проверяет очередь с именами файлов на наличие в ней необработанных пакетов, и, в случае присутствия таких, извлекает очередное имя файла, открывает сам файл и последовательно обрабатывает все находящиеся в нём документы. Имя обрабатываемого файла из очереди удаляется. Итерация заканчивается тогда, когда все обработчики завершили свою работу. На этом параллельный Е-шаг завершается, алгоритм производит последовательный М-шаг, и либо завершается, либо начинает новую внешнюю итерацию.
Ключевым моментом организации распараллеливания в среде с разделяемой памятью (а здесь она именно такая) является организация доступа различных потоков к разделяемым ресурсам. В силу ручной реализации потоков (без использования OpenMP) решение проблемы ложится на авторов кода. Как было отмечено выше, разделяемыми ресурсами являются две матрицы размера "число слов" на "число тем". Обе они имеют фиксированные размеры всё время работы алгоритма. Как было сказано, обе матрицы реализованы в виде хэш-таблиц с ключами-словами. Единицей блокировки является вектор, соответствующий одному слову. Для организации такого доступа каждая матрица хранит вектор объектов mutex, по одному на каждый ключ матрицы, и имеет методы, регулирующие, с помощью этих mutex-ов, доступ к каждой строке.
Очередь имён файлов также имеет mutex, поскольку используется всеми потоками.
2.4 Масштабируемость алгоритма и его реализации
Данная параллельная реализация тестировалась на компьютере со вычислительными следующими характеристиками:
Intel(R) Core(TM) i7-5820K @ 3.30GHz (6 физических ядер, 12 потоков, без использования аппаратного ускорения ядер).
Соответственно, максимальное количество параллельных обработчиков было равно 12. В качестве входных данных использовалась коллекция писем Х. Клинтон (точнее, её подмножество из 6000 тысяч писем, т. е. больше 80%). Вся коллекция, как было отмечено выше, делится на текстовые файлы, в каждом файле одна строка соответствует одному документу. Единицей параллелизма является файл.
Измеряемыми параметрами масштабируемости являются:
- количество тем;
- количество внутренних итераций;
- количество потоков-обработчиков.
Количество документов в каждом пакете зафиксируем равным 100. Число внешних итераций - 10.
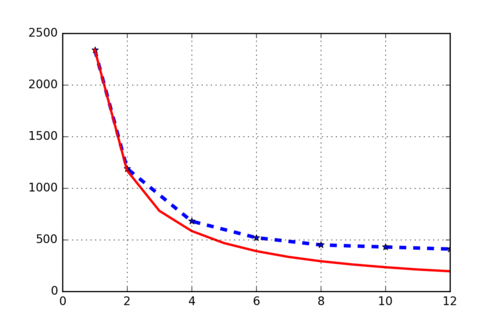
Измеряемым параметром является время работы алгоритма без учёта вспомогательных операций (сбор словаря коллекции, который реализация умеет производить однократно и далее переиспользовать сохранённый на диск результат). Для каждого фиксированного числа тем и количества внутренних итераций построен двумерный график зависимости времени работы от числа потоков, т.е. график масштабируемости алгоритма.
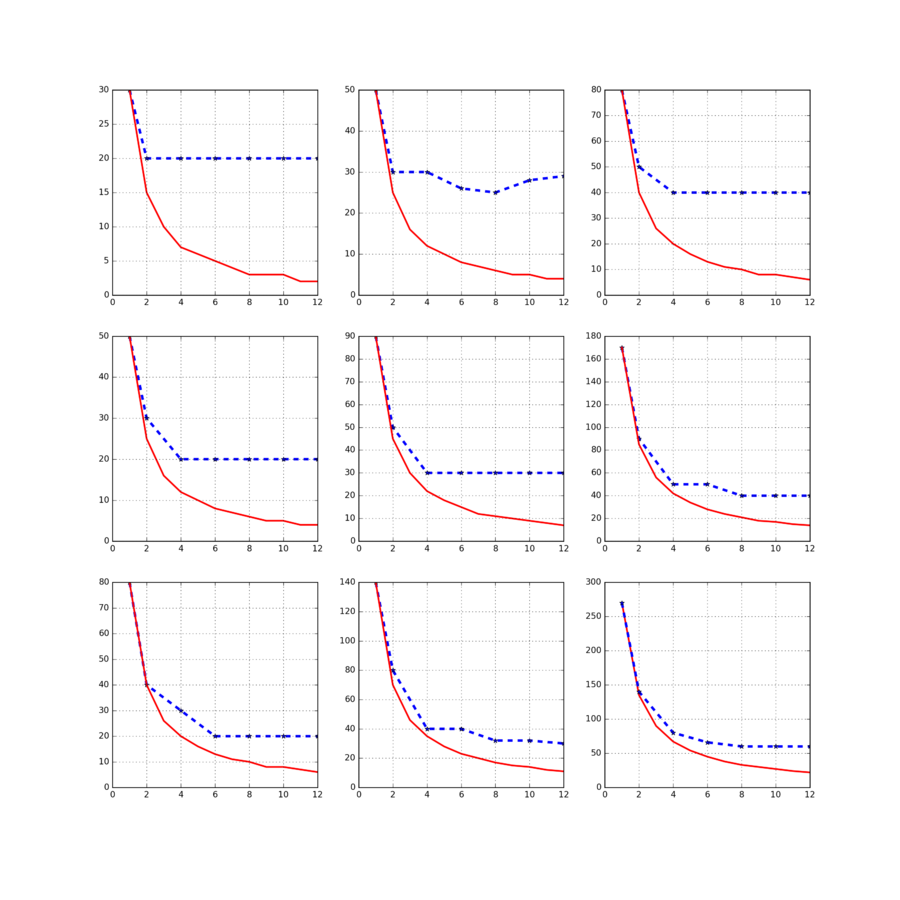
Можно заметить, что качество параллелизма постоянно растёт с увеличением нагрузки на Е-шаг, что является признаком качественной архитектуры. Вывод сделан потому, что и увеличение объёма обрабатываемых данных, и ускорение скорости сходимости модели, и увеличение числа тем - всё это является основными источниками увеличения вычислительных затрат при работе алгоритма. Получается, что алгоритм при усложнении обрабатываемой задачи показывает всё более хорошую масштабируемость. В качестве примера рассматриватся в разы усложнённая задача: 200 тем и 20 внутренних итераций на той же коллекции текстов:
Реализация алгоритма на языке C++ (STL, Boost)
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Наиболее близкой (хотя далеко не идентичной) реализацией описанного алгоритма является ЕМ-алгоритм для тематического моделирования из библиотеки BigARTM. Там реализован полноценный онлайновый ЕМ-алгоритм с относительно сложной архитектурой распараллеливания, позволяющий добиться эффективной онлайновой обработки огромных текстовых коллекций на одной машине.
Существуют и другие программные реализации алгоритмов для тематического моделирования, но большинство из них не использует ЕМ-алгоритм, или же использует его вариационный вариант, который здесь не рассматривается (хотя идеи параллелизма там используются схожие).
3 Литература
- ↑ https://ru.wikipedia.org/wiki/Тематическое_моделирование
- ↑ http://www.machinelearning.ru/wiki/index.php?title=Тематическое_моделирование
- ↑ https://en.wikipedia.org/wiki/Probabilistic_latent_semantic_analysis
- ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
- ↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.
- ↑ Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.