Участник:Dmitry/Плотностный алгоритм кластеризации: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
(Новая страница: «Авторы описания: Титов Д.Е. = Свойства и структура алгоритма = == Общее оп…»)
 
Строка 4: Строка 4:
  
 
== Общее описание алгоритма ==
 
== Общее описание алгоритма ==
 +
 +
Под кластеризацией понимается деление заданного множества точек данных (объектов) на подгруппы, каждая из которых, насколько это возможно, однородна. В основе метода кластеризации DBSCAN лежит объединение некоторых объектов в соответствии с их внутригрупповым «соединением». Для проведения корректной процедуры кластеризации необходимо указать критерии, по которым объекты будут объединены в кластеры. Прежде всего, необходимо сказать, что кластеры представляют собой плотные области некоторых объектов в пространстве данных, разделенных между собой объектами, плотность которых значительно ниже. Расположение точек в одном кластере обусловлено их соединением, т.е. некоторой связью между собой.
 +
 +
== Математическое описание алгоритма ==
 +
 +
Плотность точек для данной точки <math>X</math> определяется двумя параметрами. Первым из них является
 +
<math>\varepsilon</math> – радиус «соседства» (приближенности) точки <math>X</math>. Тогда множество <math>M(X)</math> будет включать в себя такие точки
 +
  n,1i,f
 +
i 
 +
, для которых следующее не-
 +
равенство будет истинно
 +
    n,1i,f,Xdist
 +
i  . (1).
 +
Функция
 +
)2var,1(vardist
 +
определяет расстоя-
 +
ние между объектами выборки
 +
D
 +
. Это расстояние
 +
может вычисляться различными способами,
 +
например, как евклидово расстояние или с помо-
 +
щью метрики Минковского.
 +
Вторым параметром определения плотности
 +
точек является MCP – это минимальное количество
 +
точек, которые расположены ближе всего к данной
 +
точке согласно определенному радиусу .
 +
Точка
 +
  n,1i,f
 +
i 
 +
будет являться окруженной
 +
точкой (согласно
 +
 +
и
 +
MCP
 +
) если
 +
 +
   MCPX . (2)
 +
Это значит, что точка
 +
  n,1i,f
 +
i 
 +
окружен-
 +
ная, если количество «соседствующих» точек вы-
 +
борки
 +
D
 +
окажется большим, либо равным значе-
 +
нию параметра
 +
MCP
 +
(рис. 1).
 +
Точка Х является прямо достижимой по плот-
 +
ности от точки
 +
f
 +
(при соответствующих  и
 +
MCP
 +
), если точка
 +
   XX , т.е. точка Х – это
 +
одна из точек f для другого окружения (соседства),
 +
где f – окруженная точка (рис. 2).
 +
 +
Рис. 1. Окруженная
 +
точка при МСР = 5
 +
Рис. 2. Точка Х прямо достижима
 +
по плотности от точки f
 +
Достижимость по плотности – это транзитив-
 +
ное замыкание прямо достижимой по плотности
 +
точки. Точка
 +
f
 +
достижима по плотности из точки
 +
X
 +
, но точка
 +
X
 +
не достижима по плотности из точ-
 +
ки
 +
f
 +
(рис. 3).
 +
 +
== Вычислительное ядро алгоритма ==
 +
 +
Вычислительным ядром алгоритма является нахождение <math>\varepsilon</math>-соседей каждой точки входного множества <math>X</math>.
 +
 +
Для решения этой задачи требуется найти расстояния между любыми двумя точками множества <math>X</math> по заданной метрике. Например, если используется расстояние Минковского порядка <math>k</math>, то расстояние между точками <math>p=(p_1,...,p_n) \in X</math> и <math>q=(q_1,...,q_n) \in X</math> вычисляется как <math>D(p, q) = (\sum_{i = 1}^{n}|p_i - q_i|^k)^{1 / k}</math>, частным случаем которой при <math>k = 2</math> является широко распространённая евклидова метрика <math>D(p, q) = \sqrt{\sum_{i = 1}^{n} (p_i - q_i)^2}</math>.
 +
 +
== Макроструктура алгоритма ==
 +
 +
Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют вызовы функции <math>request\_neighbours</math> получения <math>\varepsilon</math>-соседей и нахождение расстояний между точками множества <math>X</math>.
 +
 +
== Схема реализации последовательного алгоритма ==
 +
 +
 +
<math>DBSCAN</math> проходит через все точки множества <math>X</math> и определяет, являются ли они шумом или началом нового кластера.
 +
В последнем случае новому кластеру присваивается уникальный номер и вызывается функция расширения кластера.
 +
 +
<math>DBSCAN(\varepsilon, MinPts)</math>
 +
  <math>C = 0</math>
 +
  for <math>\forall p \in X</math>
 +
      if <math>p</math> is visited then
 +
        continue
 +
      mark <math>p</math> as visited
 +
      <math>neighbours</math> = <math>request\_neighbours(p, \varepsilon)</math>
 +
      if <math>| neighbours | < MinPts</math> then
 +
        mark <math>p</math> as <math>NOISE</math>
 +
      else
 +
        <math>C = next\_cluster</math>
 +
        <math>expand\_cluster(p, neighbours, C, \varepsilon, MinPts)</math>
 +
 +
<math>expand\_cluster</math> рекурсивно проходит через все точки множества <math>neighbours</math> - соседей точки <math>p</math>,
 +
и определяет, принадлежат ли эти точки тому же кластеру <math>C</math>, тем самым расширяя этот кластер.
 +
 +
<math>expand\_cluster(p, neighbours, C, \varepsilon, MinPts)</math>
 +
  add <math>p</math> to cluster <math>C</math>
 +
  for <math>\forall p' \in neighbours</math>
 +
      if <math>p'</math> is not visited
 +
        mark <math>p'</math> as visited
 +
        <math>neighbours'</math> = <math>request\_neighbours(p, \varepsilon)</math>
 +
        if <math>| neighbours' | \ \ge MinPts</math>
 +
            <math>neighbours</math> = <math>neighbours \cup neighbours'</math> 
 +
      if <math>p'</math> is not yet member of any cluster
 +
        add <math>p'</math> to cluster <math>C</math>
 +
 +
<math>request\_neighbours</math> возвращает для точки <math>p</math> множество всех её <math>\varepsilon</math>-соседей,
 +
используя функцию расстояния <math>D</math>
 +
<math>request\_neighbours(p, \varepsilon)</math>
 +
    return <math>\{ p' \ | \ \forall p' \in X: D(p, p') < \varepsilon \}</math>
 +
 +
== Последовательная сложность алгоритма ==
 +
 +
DBSCAN проходит через каждую точку входного множества, возможно, по несколько раз. Временная сложность зависит в большей степени от вызова функции <math>request\_neighbours</math> (нахождение <math>\varepsilon</math>-соседей для заданной точки). Эта функция вызывается ровно один раз для каждой точки множества <math>X</math>.
 +
 +
Если использовать индексированную структуру данных (например, R-деревья), выполняющую операцию <math>request\_neighbours</math> за <math>O(\log n)</math>, то суммарная сложность алгоритма в среднем составит <math>O(n \log n)</math>, с учётом хорошо подобранного параметра <math>\varepsilon</math>, такого что в среднем <math>request\_neighbours</math> возвращает <math>O(\log n)</math> точек. Без использования ускоряющих структур или на вырожденных данных (таких, что все точки находятся на расстоянии меньшем, чем <math>\varepsilon</math> друг от друга) сложность по времени в худшем случае будет <math>O(n^2)</math>.
 +
 +
 +
Расстояния между точками можно вычислить заранее за <math>O(\frac {n(n - 1)}{2})</math>, например в виде матрицы расстояний, но это потребует <math>O(n^2)</math> памяти. Иначе, расстояния будут вычисляться при каждом запуске функции <math>request\_neighbours</math> за <math>O(n)</math> и потребуют <math>O(n)</math> памяти. Итоговая сложность вычисления расстояний в таком случае составляет <math>O(n^2)</math>. Сложность рассчета расстояний зависит от природы объектов из <math>X</math> и заданной метрики <math>D</math>. Например, если <math>X\subset\mathbb{R}^m</math>, то сложность равна <math>O(m)</math>, но оценка может быть улучшена при использовании векторных операций.
 +
 +
== Информационный граф ==
 +
 +
Опишем граф алгоритма<ref>Воеводин В.В.  Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.</ref><ref>Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.</ref><ref>Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.</ref>.
 +
 +
 +
[[File:Dbscan abstract.png |thumb|right|320px| Рис. 2. Внешний цикл алгоритма.]]
 +
 +
 +
На рис. 2 изображен информационный граф внешнего цикла алгоритма, который соответствует коду основной функции <math>DBSCAN</math>:
 +
*Макрооперация ''Init'' заключается в получении множества <math>X</math> и инициирования вспомогательных структур.
 +
*Макрооперация ''Choose'' производит выбор непосещенной точки из <math>X</math>.
 +
*Макрооперация ''Build cluster'' строит кластер, если точка ядровая, или объявляет ее шумом.
 +
 +
 +
Переход от ''Build cluster'' к ''Choose'' заключает в себе зависимость данных о принадлежности некоторых точек к текущему кластеру или шуму и об их посещенности.
 +
 +
[[File:Expand cluster 2.png |thumb|right|600px| Рис. 3. Расширение кластера.]]
 +
 +
 +
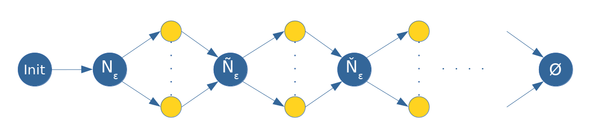
На рис. 3 изображен информационный граф алгоритма расширения кластера из начальной точки кластера:
 +
*Макрооперация ''Init'' заключается в создании кластера из его начальной вершины.
 +
*Макрооперация ''Nε'' вычисляет множество <math>\varepsilon</math>-соседей.
 +
*Желтым цветом обозначены узлы, в которых точки из <math>\varepsilon</math>-соседей классифицируются на ядровые, граничные точки и шум. В рамках операции для конкретного соседа вычисляется множество его <math>\varepsilon</math>-соседей.
 +
*Макрооперации ''Ñε'', ''Ňε'', ... производят объединение входных множеств.
 +
*Макрооперация ''Ø'' выполняется тогда, когда объединение входных множеств является пустым.
 +
 +
 +
[[File:N eps 3.png        |thumb|right|320px| Рис. 4. Подсчет <math>\varepsilon</math>-соседей.]]
 +
 +
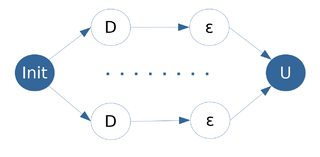
На рис. 4 изображен информационный граф алгоритма вычисления множества <math>\varepsilon</math>-соседей:
 +
*Операция ''D'' - вычисление расстояния между точками.
 +
*Операция ''ε'' - сравнение расстояния с ε.
 +
*Операция ''U'' - объединение результатов.
 +
 +
== Ресурс параллелизма алгоритма ==
 +
 +
Поиск <math>\varepsilon</math>-соседей требует вычисления <math>n</math> расстояний (функция <math>D</math>) и выполнения <math>n</math> сравнений с <math>\varepsilon</math>. Эти операции для каждой пары точек независимы и могут быть выполнены параллельно. Таким образом, при наличии неограниченного числа процессоров сложность поиска составит <math>O(1)</math>. Т.к. поиск выполняется для каждой точки ровно один раз, параллельная сложность всего алгоритма составит <math>O(n)</math>.
 +
 +
== Входные и выходные данные алгоритма ==
 +
 +
 +
Вход алгоритма: множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидово расстояние между векторами из <math>\mathbb{R}^n</math>.
 +
 +
Выход алгоритма: размеченное множество точек <math>X</math>, в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из <math>X</math> сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера <math>|X|</math>.
 +
 +
== Свойства алгоритма ==
 +
 +
Соотношение последовательной и параллельной сложностей алгоритма является линейным (отношение квадратичной к линейной).
 +
 +
При этом вычислительная мощность, как отношение числа операций к суммарному объему входных и выходных данных линейна.
 +
 +
=== Преимущества алгоритма ===
 +
 +
# не требует указывать число кластеров;
 +
# может определять кластера произвольной формы;
 +
# может определять шум и устойчив к выбросам;
 +
# требует всего два параметра и по в большинстве случаев не чувствителен к порядку заданных точек;
 +
# параллельная реализация сбалансирована по количеству и виду производимых операций (вычисление расстояния, сравнение с <math>\varepsilon</math>).
 +
 +
=== Недостатки алгоритма ===
 +
 +
# не детерминирован: граничные точки, достижимые из более, чем одного кластера, могут быть частью любого из них в зависимости от порядка обрабатываемых данных. Однако такая ситуация возникает редко, а относительно ядровых точек и шума DBSCAN детерминирован. Впрочем, от недетерминизма можно избавиться, если считать все граничные точки шумом (алгоритм DBSCAN*);
 +
# качество алгоритма зависит от используемой функции расстояния <math>D</math>. Наиболее часто используемое Евклидово расстояние в многомерных множествах может оказаться практически бесполезным из-за так называемого "проклятия размерности", значительно затрудняя нахождение подходящего значения <math>\varepsilon</math>;
 +
# не может выделять кластеры, имеющие разную плотность, так как параметры алгоритма не могут быть выбранны отдельно для каждого кластера.
 +
 +
= Программная реализация алгоритма =
 +
 +
== Особенности реализации последовательного алгоритма ==
 +
 +
== Локальность данных и вычислений ==
 +
 +
== Возможные способы и особенности параллельной реализации алгоритма ==
 +
 +
== Масштабируемость алгоритма и его реализации ==
 +
 +
!!! ЭКСПЕРИМЕНТЫ ДО 15 НОЯБРЯ !!!
 +
 +
== Динамические характеристики и эффективность реализации алгоритма ==
 +
 +
== Выводы для классов архитектур ==
 +
 +
== Существующие реализации алгоритма ==
 +
 +
* [http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html Scikit learn (Python)]
 +
* [https://cran.r-project.org/web/packages/dbscan/dbscan.pdf R-project] ([https://github.com/mhahsler/dbscan github])
 +
* [https://www.mathworks.com/matlabcentral/fileexchange/52905-dbscan-clustering-algorithm Matlab]
 +
* P-DBSCAN (Parallel DBSCAN)<ref>Chen, Min, Xuedong Gao, and HuiFei Li. "Parallel DBSCAN with priority r-tree." Information Management and Engineering (ICIME), 2010 The 2nd IEEE International Conference on. IEEE, 2010.</ref>
 +
* Parallel DBSCAN with MPI<ref>Savvas, Ilias K., and Dimitrios Tselios. "Parallelizing DBSCaN Algorithm Using MPI." Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), 2016 IEEE 25th International Conference on. IEEE, 2016.</ref>
 +
* PDSDBSCAN (Parallel Disjoint-Set DBSCAN)<ref>Patwary, Md Mostofa Ali, et al. "A new scalable parallel DBSCAN algorithm using the disjoint-set data structure." High Performance Computing, Networking, Storage and Analysis (SC), 2012 International Conference for. IEEE, 2012.</ref>
 +
 +
= Литература =
 +
 +
<references />

Версия 05:52, 20 января 2017

Авторы описания: Титов Д.Е.

Содержание

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Под кластеризацией понимается деление заданного множества точек данных (объектов) на подгруппы, каждая из которых, насколько это возможно, однородна. В основе метода кластеризации DBSCAN лежит объединение некоторых объектов в соответствии с их внутригрупповым «соединением». Для проведения корректной процедуры кластеризации необходимо указать критерии, по которым объекты будут объединены в кластеры. Прежде всего, необходимо сказать, что кластеры представляют собой плотные области некоторых объектов в пространстве данных, разделенных между собой объектами, плотность которых значительно ниже. Расположение точек в одном кластере обусловлено их соединением, т.е. некоторой связью между собой.

1.2 Математическое описание алгоритма

Плотность точек для данной точки [math]X[/math] определяется двумя параметрами. Первым из них является [math]\varepsilon[/math] – радиус «соседства» (приближенности) точки [math]X[/math]. Тогда множество [math]M(X)[/math] будет включать в себя такие точки   n,1i,f i  , для которых следующее не- равенство будет истинно     n,1i,f,Xdist i  . (1). Функция )2var,1(vardist 

определяет расстоя-

ние между объектами выборки D . Это расстояние может вычисляться различными способами, например, как евклидово расстояние или с помо- щью метрики Минковского. Вторым параметром определения плотности точек является MCP – это минимальное количество точек, которые расположены ближе всего к данной точке согласно определенному радиусу . Точка   n,1i,f i  

будет являться окруженной

точкой (согласно  и MCP ) если     MCPX . (2) Это значит, что точка   n,1i,f i  

окружен-

ная, если количество «соседствующих» точек вы- борки D 

окажется большим, либо равным значе-

нию параметра MCP 

(рис. 1).

Точка Х является прямо достижимой по плот- ности от точки f 

(при соответствующих  и

MCP ), если точка    XX , т.е. точка Х – это одна из точек f для другого окружения (соседства), где f – окруженная точка (рис. 2).

Рис. 1. Окруженная точка при МСР = 5 Рис. 2. Точка Х прямо достижима по плотности от точки f Достижимость по плотности – это транзитив- ное замыкание прямо достижимой по плотности точки. Точка f 

достижима по плотности из точки

X , но точка X 

не достижима по плотности из точ-

ки f 

(рис. 3).

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является нахождение [math]\varepsilon[/math]-соседей каждой точки входного множества [math]X[/math].

Для решения этой задачи требуется найти расстояния между любыми двумя точками множества [math]X[/math] по заданной метрике. Например, если используется расстояние Минковского порядка [math]k[/math], то расстояние между точками [math]p=(p_1,...,p_n) \in X[/math] и [math]q=(q_1,...,q_n) \in X[/math] вычисляется как [math]D(p, q) = (\sum_{i = 1}^{n}|p_i - q_i|^k)^{1 / k}[/math], частным случаем которой при [math]k = 2[/math] является широко распространённая евклидова метрика [math]D(p, q) = \sqrt{\sum_{i = 1}^{n} (p_i - q_i)^2}[/math].

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют вызовы функции [math]request\_neighbours[/math] получения [math]\varepsilon[/math]-соседей и нахождение расстояний между точками множества [math]X[/math].

1.5 Схема реализации последовательного алгоритма

[math]DBSCAN[/math] проходит через все точки множества [math]X[/math] и определяет, являются ли они шумом или началом нового кластера. В последнем случае новому кластеру присваивается уникальный номер и вызывается функция расширения кластера. 

[math]DBSCAN(\varepsilon, MinPts)[/math]
  [math]C = 0[/math]
  for [math]\forall p \in X[/math]
     if [math]p[/math] is visited then
        continue
     mark [math]p[/math] as visited
     [math]neighbours[/math] = [math]request\_neighbours(p, \varepsilon)[/math]
     if [math]| neighbours | \lt  MinPts[/math] then
        mark [math]p[/math] as [math]NOISE[/math]
     else
        [math]C = next\_cluster[/math]
        [math]expand\_cluster(p, neighbours, C, \varepsilon, MinPts)[/math]

[math]expand\_cluster[/math] рекурсивно проходит через все точки множества [math]neighbours[/math] - соседей точки [math]p[/math], и определяет, принадлежат ли эти точки тому же кластеру [math]C[/math], тем самым расширяя этот кластер. 

[math]expand\_cluster(p, neighbours, C, \varepsilon, MinPts)[/math]
  add [math]p[/math] to cluster [math]C[/math]
  for [math]\forall p' \in neighbours[/math]
     if [math]p'[/math] is not visited 
        mark [math]p'[/math] as visited
        [math]neighbours'[/math] = [math]request\_neighbours(p, \varepsilon)[/math]
        if [math]| neighbours' | \ \ge MinPts[/math]
           [math]neighbours[/math] = [math]neighbours \cup neighbours'[/math]  
     if [math]p'[/math] is not yet member of any cluster
        add [math]p'[/math] to cluster [math]C[/math]

[math]request\_neighbours[/math] возвращает для точки [math]p[/math] множество всех её [math]\varepsilon[/math]-соседей, используя функцию расстояния [math]D[/math] 

[math]request\_neighbours(p, \varepsilon)[/math]
   return [math]\{ p' \ | \ \forall p' \in X: D(p, p') \lt  \varepsilon \}[/math]

1.6 Последовательная сложность алгоритма

DBSCAN проходит через каждую точку входного множества, возможно, по несколько раз. Временная сложность зависит в большей степени от вызова функции [math]request\_neighbours[/math] (нахождение [math]\varepsilon[/math]-соседей для заданной точки). Эта функция вызывается ровно один раз для каждой точки множества [math]X[/math].

Если использовать индексированную структуру данных (например, R-деревья), выполняющую операцию [math]request\_neighbours[/math] за [math]O(\log n)[/math], то суммарная сложность алгоритма в среднем составит [math]O(n \log n)[/math], с учётом хорошо подобранного параметра [math]\varepsilon[/math], такого что в среднем [math]request\_neighbours[/math] возвращает [math]O(\log n)[/math] точек. Без использования ускоряющих структур или на вырожденных данных (таких, что все точки находятся на расстоянии меньшем, чем [math]\varepsilon[/math] друг от друга) сложность по времени в худшем случае будет [math]O(n^2)[/math].


Расстояния между точками можно вычислить заранее за [math]O(\frac {n(n - 1)}{2})[/math], например в виде матрицы расстояний, но это потребует [math]O(n^2)[/math] памяти. Иначе, расстояния будут вычисляться при каждом запуске функции [math]request\_neighbours[/math] за [math]O(n)[/math] и потребуют [math]O(n)[/math] памяти. Итоговая сложность вычисления расстояний в таком случае составляет [math]O(n^2)[/math]. Сложность рассчета расстояний зависит от природы объектов из [math]X[/math] и заданной метрики [math]D[/math]. Например, если [math]X\subset\mathbb{R}^m[/math], то сложность равна [math]O(m)[/math], но оценка может быть улучшена при использовании векторных операций.

1.7 Информационный граф

Опишем граф алгоритма[1][2][3].


Рис. 2. Внешний цикл алгоритма.


На рис. 2 изображен информационный граф внешнего цикла алгоритма, который соответствует коду основной функции [math]DBSCAN[/math]:

  • Макрооперация Init заключается в получении множества [math]X[/math] и инициирования вспомогательных структур.
  • Макрооперация Choose производит выбор непосещенной точки из [math]X[/math].
  • Макрооперация Build cluster строит кластер, если точка ядровая, или объявляет ее шумом.


Переход от Build cluster к Choose заключает в себе зависимость данных о принадлежности некоторых точек к текущему кластеру или шуму и об их посещенности.

Рис. 3. Расширение кластера.


На рис. 3 изображен информационный граф алгоритма расширения кластера из начальной точки кластера:

  • Макрооперация Init заключается в создании кластера из его начальной вершины.
  • Макрооперация Nε вычисляет множество [math]\varepsilon[/math]-соседей.
  • Желтым цветом обозначены узлы, в которых точки из [math]\varepsilon[/math]-соседей классифицируются на ядровые, граничные точки и шум. В рамках операции для конкретного соседа вычисляется множество его [math]\varepsilon[/math]-соседей.
  • Макрооперации Ñε, Ňε, ... производят объединение входных множеств.
  • Макрооперация Ø выполняется тогда, когда объединение входных множеств является пустым.


Рис. 4. Подсчет [math]\varepsilon[/math]-соседей.

На рис. 4 изображен информационный граф алгоритма вычисления множества [math]\varepsilon[/math]-соседей:

  • Операция D - вычисление расстояния между точками.
  • Операция ε - сравнение расстояния с ε.
  • Операция U - объединение результатов.

1.8 Ресурс параллелизма алгоритма

Поиск [math]\varepsilon[/math]-соседей требует вычисления [math]n[/math] расстояний (функция [math]D[/math]) и выполнения [math]n[/math] сравнений с [math]\varepsilon[/math]. Эти операции для каждой пары точек независимы и могут быть выполнены параллельно. Таким образом, при наличии неограниченного числа процессоров сложность поиска составит [math]O(1)[/math]. Т.к. поиск выполняется для каждой точки ровно один раз, параллельная сложность всего алгоритма составит [math]O(n)[/math].

1.9 Входные и выходные данные алгоритма

Вход алгоритма: множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидово расстояние между векторами из [math]\mathbb{R}^n[/math].

Выход алгоритма: размеченное множество точек [math]X[/math], в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из [math]X[/math] сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера [math]|X|[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложностей алгоритма является линейным (отношение квадратичной к линейной).

При этом вычислительная мощность, как отношение числа операций к суммарному объему входных и выходных данных линейна.

1.10.1 Преимущества алгоритма

  1. не требует указывать число кластеров;
  2. может определять кластера произвольной формы;
  3. может определять шум и устойчив к выбросам;
  4. требует всего два параметра и по в большинстве случаев не чувствителен к порядку заданных точек;
  5. параллельная реализация сбалансирована по количеству и виду производимых операций (вычисление расстояния, сравнение с [math]\varepsilon[/math]).

1.10.2 Недостатки алгоритма

  1. не детерминирован: граничные точки, достижимые из более, чем одного кластера, могут быть частью любого из них в зависимости от порядка обрабатываемых данных. Однако такая ситуация возникает редко, а относительно ядровых точек и шума DBSCAN детерминирован. Впрочем, от недетерминизма можно избавиться, если считать все граничные точки шумом (алгоритм DBSCAN*);
  2. качество алгоритма зависит от используемой функции расстояния [math]D[/math]. Наиболее часто используемое Евклидово расстояние в многомерных множествах может оказаться практически бесполезным из-за так называемого "проклятия размерности", значительно затрудняя нахождение подходящего значения [math]\varepsilon[/math];
  3. не может выделять кластеры, имеющие разную плотность, так как параметры алгоритма не могут быть выбранны отдельно для каждого кластера.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

!!! ЭКСПЕРИМЕНТЫ ДО 15 НОЯБРЯ !!!

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

  1. ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
  2. ↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.
  3. ↑ Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.
  4. ↑ Chen, Min, Xuedong Gao, and HuiFei Li. "Parallel DBSCAN with priority r-tree." Information Management and Engineering (ICIME), 2010 The 2nd IEEE International Conference on. IEEE, 2010.
  5. ↑ Savvas, Ilias K., and Dimitrios Tselios. "Parallelizing DBSCaN Algorithm Using MPI." Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), 2016 IEEE 25th International Conference on. IEEE, 2016.
  6. ↑ Patwary, Md Mostofa Ali, et al. "A new scalable parallel DBSCAN algorithm using the disjoint-set data structure." High Performance Computing, Networking, Storage and Analysis (SC), 2012 International Conference for. IEEE, 2012.
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Dmitry/Плотностный_алгоритм_кластеризации&oldid=21629