Участник:Ilya365365/Алгоритм кластеризации категориальных данных: различия между версиями
| Строка 16: | Строка 16: | ||
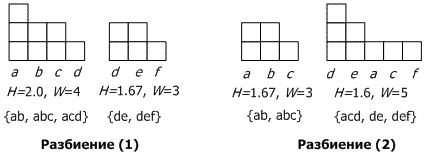
Для первого и второго вариантов разбиения в каждом кластере рассчитаем количество вхождений в него каждого элемента транзакции, а затем вычислим ширину <math>W(c_i)</math> (количество уникальных объектов кластера), общее число объектов в кластере <math>S(C_i)</math> и высоту <math>H(C_i) = \frac{S(C_i)}{W(C_i)^r}</math>, где <math>r</math> - коэффициент отталкивания. Чем больше <math>r</math>, тем больше кластеров будет сгенерировано. Например, кластер {ab, abc, acd} имеет вхождения a:3, b:2, c:2, d:1 с H=2 и W=4, при r = 1. | Для первого и второго вариантов разбиения в каждом кластере рассчитаем количество вхождений в него каждого элемента транзакции, а затем вычислим ширину <math>W(c_i)</math> (количество уникальных объектов кластера), общее число объектов в кластере <math>S(C_i)</math> и высоту <math>H(C_i) = \frac{S(C_i)}{W(C_i)^r}</math>, где <math>r</math> - коэффициент отталкивания. Чем больше <math>r</math>, тем больше кластеров будет сгенерировано. Например, кластер {ab, abc, acd} имеет вхождения a:3, b:2, c:2, d:1 с H=2 и W=4, при r = 1. | ||
| + | |||
[[Файл:Clope split.png|border|Гистограммы разбиений]] | [[Файл:Clope split.png|border|Гистограммы разбиений]] | ||
| − | Лучшим признаётся разбиение, при котором достигается максимум функции <math> Profit(C)=\frac{\sum^{k}_{i=1} H(C_i) \times \mid C_i \mid} { | + | Лучшим признаётся разбиение, при котором достигается максимум функции <math> Profit(C)=\frac{\sum^{k}_{i=1} H(C_i) \times \mid C_i \mid} {M} </math> = <math>\frac{\sum^{k}_{i=1} \frac {S(C_i)}{{W(C_i)}^r} \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid} </math> |
| − | Здесь <math>k</math> - количество кластеров, <math>C_i</math>, <math>\mid C_i \mid</math> - число транзакций в кластере <math> C_i </math>. | + | Здесь <math>k</math> - количество кластеров, <math>C_i</math>, <math>\mid C_i \mid</math> - число транзакций в кластере <math> C_i </math>, M - число транзакций в выборке. |
=== Математическое описание алгоритма CLOPE === | === Математическое описание алгоритма CLOPE === | ||
Версия 20:59, 31 января 2017
Содержание
1 Свойства и структура алгоритма CLOPE
1.1 Общее описание алгоритма CLOPE
Алгоритм CLOPE решает задачу кластеризации категориальных транзакционных данных. Алгоритм основан на эвристическом методе повышения близости транзакций в кластерах при помощи оптимизации параметров кластерной гистограммы. Авторы (Yiling Yang Xudong Guan Jinyuan You )[1] предложили эффективный, масштабируемый алгоритм, не требующий хранения обучающей выборки в оперативной памяти.
Здесь и далее под категориальными данными понимаются качественные характеристики объектов, измеренные в шкале наименований, то есть при сравнении категориальных данных указывается только, одинаковы или нет объекты относительно данного признака.
Под термином транзакция понимается произвольный набор объектов, например, список ключевых слов статьи, товары, купленные в супермаркете, множество симптомов пациента, характерные фрагменты изображения и так далее. Задача кластеризации транзакционных данных состоит в получении такого разбиения всего множества транзакций, чтобы похожие транзакции оказались в одном кластере, а отличающиеся друг от друга – в разных кластерах.
В основе алгоритма кластеризации CLOPE лежит идея максимизации глобальной функции стоимости, которая повышает близость транзакций в кластерах при помощи увеличения параметра кластерной гистограммы. Для примера рассмотрим выборку из пяти списков покупок: {(apple, banana), (apple, banana, cake), (apple, cake, dish), (dish, egg), (dish, egg, fish)}, или сокращённо {ab, abc, acd, de, def}. Каждый список - транзакция. Каждый купленный предмет является объектом. Представим себе, что мы хотим сравнить между собой следующие два разбиения на кластеры:
1: {{ab, abc, acd}, {de, def}}
2: {{ab, abc}, {acd, de, def}}.
Для первого и второго вариантов разбиения в каждом кластере рассчитаем количество вхождений в него каждого элемента транзакции, а затем вычислим ширину [math]W(c_i)[/math] (количество уникальных объектов кластера), общее число объектов в кластере [math]S(C_i)[/math] и высоту [math]H(C_i) = \frac{S(C_i)}{W(C_i)^r}[/math], где [math]r[/math] - коэффициент отталкивания. Чем больше [math]r[/math], тем больше кластеров будет сгенерировано. Например, кластер {ab, abc, acd} имеет вхождения a:3, b:2, c:2, d:1 с H=2 и W=4, при r = 1.
Лучшим признаётся разбиение, при котором достигается максимум функции [math] Profit(C)=\frac{\sum^{k}_{i=1} H(C_i) \times \mid C_i \mid} {M} [/math] = [math]\frac{\sum^{k}_{i=1} \frac {S(C_i)}{{W(C_i)}^r} \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid} [/math]
Здесь [math]k[/math] - количество кластеров, [math]C_i[/math], [math]\mid C_i \mid[/math] - число транзакций в кластере [math] C_i [/math], M - число транзакций в выборке.
1.2 Математическое описание алгоритма CLOPE
1.3 Вычислительное ядро
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
1.6 Информационный граф
1.7 Ресурс параллелизма
1.8 Входные и выходные данные
- ↑ Y. Yang, X. Guan J. You. CLOPE: A Fast and Effective Clustering Algorithm for Transactional Data. http://www.inf.ufrgs.br/~alvares/CMP259DCBD/clope.pdf