Участник:Anton goy/Самоорганизующиеся карты Кохонена: различия между версиями
Anton goy (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 9 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Assignment|ASA}} | |
Автор: [[U:Anton goy|Гой Антон]], 617 группа. | Автор: [[U:Anton goy|Гой Антон]], 617 группа. | ||
| − | |||
= Свойства и структура алгоритмов = | = Свойства и структура алгоритмов = | ||
| Строка 241: | Строка 240: | ||
В данном разделе мы рассмотрим паралелльную реализацию алгоритма, которая основана на разделении входной выборки по всем доступным процессам. Каждый процесс работает со своим кусоком данным и в конце каждой итерации все процессы синхронизируют состояние весов нейронов. В качестве допущения мы будем рассматривать только одну итерацию алгоритма (если итераций больше чем одна, то результаты просто будут отличаться на множитель равный количеству итераций). Кроме того, допустим <math>B = N</math>. | В данном разделе мы рассмотрим паралелльную реализацию алгоритма, которая основана на разделении входной выборки по всем доступным процессам. Каждый процесс работает со своим кусоком данным и в конце каждой итерации все процессы синхронизируют состояние весов нейронов. В качестве допущения мы будем рассматривать только одну итерацию алгоритма (если итераций больше чем одна, то результаты просто будут отличаться на множитель равный количеству итераций). Кроме того, допустим <math>B = N</math>. | ||
| − | Все эксперименты были выполнены на суперкомпьютере IBM Blue Gene/P. Выборка была сгенерировна из стандартного нормального распределения для <math>N = D = 1000</math>. | + | Все эксперименты были выполнены на суперкомпьютере IBM Blue Gene/P. Выборка была сгенерировна из стандартного нормального распределения для <math>N = D = 1000</math>. Набор изменяемых параметров запуска: |
| + | |||
| + | # <math>L</math> (число нейронов с решетке) = [ 1024, 4096, 9216, 16384, 25600, 36864, 50176, 65536] | ||
| + | # <math>P</math> (число процессоров) = [ 8, 16, 32, 48, 64, 128, 384, 256, 512] | ||
| + | |||
| + | Для оценки производительности (GFLOPS) была использована оценка числа операций приведенная ранее. | ||
| + | |||
| + | На Рис 6 показана зависимость производительности алгоритма от числа процессоров и количества нейронов в решетке. График подтверждает наше интуитивную догадку, что для больших размеров решетки алгоритм имеет большую производительность в терминах операций с плавающей точкой. Максимальная производитлеьность 24 GFLOPS достигается на 512 процессорах и для 50176 (224 * 224) нейронов. Минимальная же производительность (0.6 GFLOPS) наблюдается на 8 процессорах при любом числе нейронов. | ||
| + | |||
| + | [[File:Performance som1.png|1000px|thumb|center|Рисунок 6. Производительность алгоритма SOM]] | ||
| + | |||
| + | На Рис 7 показана аналогичная зависимость эффективности реализации. Здесь стоит отметить, что эффективность реализации очень низкая (в среднем 2% от пиковой производительности). Это долольно просто объяснить: в алгоритме требуется передовать больше количество данных (веса нейронов) для синхронизации процессов, поэтому значительную часть времени процессоры простаивают, ожидая передачи или отправки данных. Данная ситуация ухудшается, когда нейронов становится больше, что отлично видно на графике. Максимальная эффектвность (2.7 %) была достигнута для 8 процессов и остается неизменной при любом числе нейрнов, в данном случае более высокая эффективность достигается за счет того, что требуется осуществить синхронизацию только между 8 процессами, что намного дешевле, чем в случае 512 процессоров (минимально достигнутая эффективость - 1%). | ||
| − | + | [[File:Efficiency som1.png|1000px|thumb|center|Рисунок 7. Эффективность алгоритма SOM]] | |
| − | + | В целом можно отметить, что алгоритм обладает свойством сильной масштабируемости: на Рис 6 можно наблюдать сублинейный рост производительности с ростом числа процессоров при фиксированном числе нейронов. Так же заметим, что алгоритм проявляет свойство слабой масштабируемости: так, например, при <math>W / p = 128</math> отмечаем следующий рост производительности: [0.61, 2.17, 7.92, 21.4] при соответствующих значенияз числа процессоров: [8, 32, 128, 512]. Другой пример: <math>W / p = 64</math>, производительности - [1.21, 4.17, 12.96] при [16, 64, 256]. | |
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
Текущая версия на 10:54, 6 февраля 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 06.02.2017 Данная работа соответствует формальным критериям. Проверено ASA. |
Автор: Гой Антон, 617 группа.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Самоорганизующаяся карта Кохонена (англ. Self-Organizing Map или сокращено SOM) - это разновидность нейронных сетей, относящаяся к алгоритмам обучения без учителя. Основная цель - найти скрытые закономерности в данных по средством снижения размерности исходного пространства. Важным свойством карт Кохонена является то, что они строят отображение в пространство низкой размерности (обычно двумерное) таким образом, что топология исходного пространства сохраняется. Результат данного отображения - правильная решетка из обученных нейронов - называется "картой" исходного пространства. Алгоритм был разработан известным финским учёным, заслуженным академиком Финской Академии Наук Теуво Кохоненом в 1984(2) году. Карты Кохенана находят успешное применение в задачах кластеризации и визуализации, а также для снижения размерности и детектирования аномалий в данных.
Карты Кохонена и по своей архитектуре, и по методу обучения отличаются от обычных нейронных сетей прямого распространения. C точки зрения метода обучения, карты Кохонена не используют градиентные методы для минимизации ошибки (как это делается в сетях прямого распространения), поскольку являются алгоритмом обучения без учителя и никак не могут учитывать информацию и метках классов. Поэтому нейронная сеть обучается через соревнование между нейронами: на каждом шаге алгоритма для случайного объекта из обучающей выборки выбирается нейрон-победитель (best matching unit, BMU), который в определенном смысле наиболее похож на данный объект.
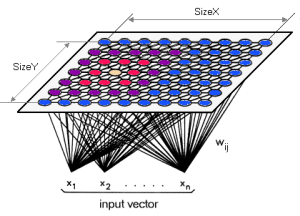
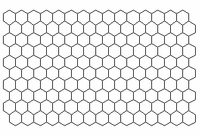
А архитектура карты Кохонена (Рис. 1) представляет два слоя: первый слой состоит из входных нейронов (их количество равно размерности исходного пространства), второй слой (его называют слоем Кохонена) представляет собой строго упорядоченную решетку, в узлах которой расположены нейроны-сумматоры, соедененные со всеми входами сети. Для визуализации топологии слоя Кохонена (Рис. 2) используют либо шестиугольные (Рис. 2а), либо прямоугольные (Рис. 2б) ячейки, в которых распологаются нейроны. Шестиугольные ячейки часто являются более предпочтительными, так как расстояние от центра выбранной ячейки до ее соседей одинаково.
Каждый нейрон n_j слоя Кохонена описывается вектором весов \mathbf{w}_j, размерность которого совпадает с размерностью исходного пространства, и координатами нейрона на двумерной плоскости - \mathbf{r}_j.
Процесс обучения состоит в настройке векторов весов \mathbf{w}_j.
1.2 Математическое описание алгоритма
Пусть \mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N} - некоторое подмножество точек пространства \mathbb{R}^D, \mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D. В машинном обучении множество \mathcal{L} называют обучающей выборкой.
Пусть задано L = X \times Y общее количество нейронов в слое Кохонена. И каждому нейрону n_j поствлен в соответствие вектор весов \mathbf{w}_{j} = \left( w_{j}^{(1)}, \dots, w_{j}^{(D)} \right) \in \mathbb{R}^D и вектор \mathbf{r}_j \in \mathbb{R}^2, определющий его положение на двумерной плоскости.
Алгоритм обучения (online version):
- Задать начальные приближение весов \mathbf{w}_{j}, \forall j=1, \dots, L.
- Выбрать случайно номер объекта i \sim Unif[1, N].
- Найти расстояние между объектом \mathbf{x}_i и всеми векторами весов \mathbf{w}_{j}: \rho(\mathbf{x}_i, \mathbf{w}_{j}) = \left\| \mathbf{x}_i - \mathbf{w}_{j} \right\|^2, \quad \forall j=1, \dots, L
- Найти нейрон-победитель n_b наиболее близкий к текущему объекту \mathbf{x}_i, где b = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\mathbf{x}_i, \mathbf{w}_{j}).
- Для всех неронов n_j пересчитать их веса по следующей формуле: \mathbf{w}_{j} \leftarrow \mathbf{w}_{j} + \alpha(t)h_{b, j}(t)(\mathbf{x}_i - \mathbf{w}_{j}), где \alpha(t) - темп обучения (learning rate), монотонно убывающая функция от номера итерации t, h_{b, j}(t) - функция определяющая "меру соседства" нейронов n_b и n_j.
- Проверить критерий останова. При необходмости перейти на шаг 2.
Данное выше описание является довольно общим и не раскрывает некоторых деталей:
- Начальное приближение для \mathbf{w}_j
- Инициализация случайными значениями. Самый простой способ - w_j^{(d)} \sim Unif[0, 1]. Данный подход может потребовать большое количество итераций, так как вектора весов неупорядочены и могут находится на значительном расстоянии от точек обучающей выборки.
- Инициализация объектами обучающей выборки. Данный способ может позволить уменьшить количество итераций, так как вектора весов будут изначально находятся в области пространства, в которой расположены объекты выборки. Но проблема с неупорядоченностью остается.
- Инициализация при помощи PCA. При помощи PCA находятся первые две главные компоненты e_1, e_2. Затем в плоскости натянутой на ветора e_1, e_2 выбирается регулярная сетка точек, которыми и инициализируются вектора \mathbf{w}_j. Этот способ является наиболее предпочтительным и на практике показывает хорошие результаты.
- Задание \alpha(t)
- \alpha(t) = \alpha_0 \exp \left\{ -\frac{t}{\lambda} \right\}
- \alpha(t) = \frac{1}{t}
- \alpha(t) = \lambda^{\frac{t}{T}}, \lambda \in (0, 1)
- Задание h_{b,j}(t)
- Наиболее популярный способ: h_{b,j}(t) = \exp \left\{ - \frac{\| \mathbf{r}_b -\mathbf{r}_j \|^2}{2\sigma(t)^2} \right\}, где \sigma(t) - убывающая функция, которую можно интерпретировать как величину пропорциональную радиусу соседства. Концептуально принцип действия такой меры соседства можно представить следующим образом: пусть в точке \mathbf{r}_b задана окружность с радиусом пропорциональным \sigma(t), тогда за пределом этой окружности степень соседства становится пренебрежимо мала. Пример: \sigma(t) = \frac{\sigma_0}{1 + \frac{t}{T}}, где \sigma_0 = \max \left\{ \frac{X}{2}, \frac{Y}{2} \right\} , T - максимальное количество итераций. Для достижения лучших результатов на практике процедуру обучения разбивают на два этапа: первый этап - итерации выполняются с очень большим радиусом, что позволяет сойтись в хоррошую область быстро, а второй этап - радиус выбирается маленьким и постепенно уменьшается, что дает возможность весам более точно уловить зависимости из обучающей выборки.
- Существуют более разреженные меры сходства, например, присваивающие ненулевые веса, только внутри некоторого радиуса. Такие меры сходства могут значительно ускорить вычисления, так как не требуется вычислять меру сходства для всех нейронов.
Кроме онлайн алгоритма обучения часто на практике применяют более эффективную с точки зрения вычислений batch-версию. Пусть выбрано B \in \mathbb{N}. Тогда batch-версия алгоритма описывается следующим образом:
Алгоритм обучения (batch version):
- Задать начальные приближение весов \mathbf{w}_{j}, \forall j=1, \dots, L.
- Случайно выбрать множество \mathcal{B} \subseteq \{1, \dots, N \} размера B.
- Для каждого объекта \mathbf{x}_i, i \in \mathcal{B}, найти нейрон-победитель n_{b(i)}, где b(i) = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\mathbf{x}_i, \mathbf{w}_{j})
- Пересчитать веса для всех нейронов \mathbf{w}_j \leftarrow \frac{\sum_{i \in \mathcal{B}}h_{b(i),j}\mathbf{x}_i}{\sum_{i \in \mathcal{B}}h_{b(i),j}}, \forall j=1, \dots, L.
- Проверить критерий останова. При необходимости перейти на шаг 2.
Интерпретация шага 2 состоит в следующем: веса нейронов преставляют собой выпуклую комбинацию объектов с номерами из \mathcal{B}. Часто на практике полагают \mathcal{B} = \{1, \dots, N\}, то есть на каждой итерации мы совершаем полный проход по всей выборке объектов.
Выходом алгоритма можно считать веса нейронов, которые затем можно использовать для различных визуализаций и определния кластерной структуры обучающей выборки.
1.3 Вычислительное ядро алгоритма
Рассмотрим batch-версию алгоритма. Основные вычисления приходятся на шаг 2, где необходимо вычислять расстояния между всеми \mathbf{x}_i, i \in \mathcal{B} и весами нейронов \mathbf{w}_j, j \in \{ 1, \dots, L \} и затем искать минимум:
d_{ij} = \left\| \mathbf{x}_i - \mathbf{w}_j \right\|^2 = \left\|\mathbf{x}_i\right\|^2 - 2 \mathbf{x}_i^{T}\mathbf{w}_j + \left\|\mathbf{w}_j\right\|^2
Так как нас будет интересовать минимум по j, то первое слагаемое \left\|\mathbf{x}_i\right\|^2 можно не учитывать. Тогда все что нам нужно это вычислить матрицу квази-расстояний \mathbf{D} = \| \hat{d}_{ij} \|_{B \times L}, где \hat{d}_{ij} = \left\|\mathbf{w}_j\right\|^2 - 2 \mathbf{x}_i^{T}\mathbf{w}_j
Сложность вычисления \mathbf{D} составляет O\left(L D B \right), учитывая что \left\|\mathbf{w}_j\right\|^2 можно вычислить за один проход по всем нейронам.
Еще одной вычислительно интенсивной частью является вычисление \mathbf{w}_j. Здесь мы можем вычислить все необходимые h_{b,j}(t), а затем, используя эти значения, найти новые приблидения для \mathbf{w}_j.
1.4 Макроструктура алгоритма
Пусть \mathbf{X}_{\mathcal{B}} - матрица, строками которой являются объекты \mathbf{x}_i таких, что i \in \mathcal{B}, а \mathbf{W} - матрица, строками которой являются веса нейронов.
Тогда на макроуровне можно выделить следующие операции:
- \mathbf{D} \leftarrow ComputePairwiseDistances(\mathbf{X}_{\mathcal{B}}, \mathbf{W})
- \mathbf{b} \leftarrow FindClosestNeurons(\mathbf{D})
- \mathbf{W} \leftarrow ComputeWeightedSumsAcrossObjects(\mathbf{X}_{\mathcal{B}}, \mathbf{b})
Здесь мы дали описание макроопераций в терминах функций, возвращающих соответствующии значения.
Функция ComputePairwiseDistances вычисляет квазирасстояния между объектами и нейронами и возвращает матрицу \mathbf{D} \in \mathbb{R}^{B \times L}.
Функция FindClosestNeurons в каждой строке матрицы \mathbf{D} находит минимальное значение и возвращает вектор \mathbf{b} \in \mathbb{R}^B, такой что элемент в позиции i соответствует номеру нейрона-победителя для объекта \mathbf{x}_i.
Функция ComputeWeightedSumsAcrossObjects вычисляет новые значения весов для каждого нейрона, суммируя строки матрицы \mathbf{X}_{\mathcal{B}} с весами пропорциональными их мере соседства с соответствующим нейроном-победителем. Неявно данная функция также использует вектор положений \mathbf{r}_j нейронов на двумерной плоскости, но так как эти положения остаются неизменными в продолжении всего обучения, мы не будем указывать их явно в аргументах.
Если рассмотреть вычисления выше описанных функций, то можно также выделить следующий набор макроопераций более низкого порядка, которые используются выше определенными функциями:
- \mathbf{x}^{T} \mathbf{y} - скалярное произведение двух вектров;
- \alpha \mathbf{x} - умножение вектора на скаляр;
- \mathbf{x} + \mathbf{y} - поэлементное сложение двух векторов;
- \min_i x_i - поиск минимального элемента в векторе \mathbf{x};
- Вычисление функции h_{b,j}(t).
1.5 Схема реализации последовательного алгоритма
В этой секции, используя макрооперции из предыдущего раздела, дадим очень краткий псевдокод batch-версии алгоритма, который легко позволяет понимать основные строительные блоки данного алгоритма:
\begin{align} \mathbf{W} := &InitializeWeights() \\ \mathbf{R} := &InitializeNeuronPositionsOnPlane() \\ \mathbf{FOR} & \ t=1 \ \mathbf{TO} \ T \ \mathbf{DO} \\ & \mathcal{B} \leftarrow RandomSample\left( \{1, \dots, N\} \right) \\ & \mathbf{D} \leftarrow ComputePairwiseDistances(\mathbf{X}_{\mathcal{B}}, \mathbf{W}) \\ \quad & \mathbf{b} \leftarrow FindClosestNeurons(\mathbf{D}) \\ \quad & \mathbf{W} \leftarrow ComputeWeightedSumsAcrossObjects(\mathbf{X}_{\mathcal{B}}, \mathbf{b}) \\ \end{align}
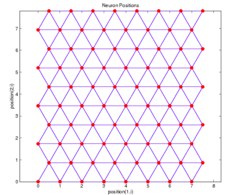
Здесь мы использовали \mathbf{R} \in \mathbb{R}^{L \times 2} как обозначение для матрицы, строками которой являются \mathbf{r}_j. Способ инициализации этих векторов для решетки с шестиугольными ячейками показан на Рис. 3. Кроме того, стоит отметить, что при нам никто не запрещает посчитать расстояния между положениями нейронов на двумерной сетки заранее, до основного цикла алгоритма. Это позволит на при подсчете меры соседства h_{b,j}(t) использовать уже вычисленные \rho(\mathbf{r}_b, \mathbf{r}_j).
Как видно из алгоритма, основной структурой данных, которая нам потребуется, будет обычная матрица, а также вектора. Стоит отметить, что алгоритм в целом неплохо оптимизируем в терминах матричных и веторных операций. Например, вычисление матрицы \mathbf{D} на языке Python с использованием библиотеки оптимизированных матричных вычислений NumPy будет выглядить следующим образом:
W_norms = numpy.linalg.norm(W, axis=1)^2 # Вычисляем квадрат нормы для каждого вектора весов
D = W_norms.T - 2 * numpy.dot(X, W.T) # Вычисляем матрицу квазирасстояний
А вычисление вектора \mathbf{b} можно реализовать всего одной строчкой:
b = D.argmin(axis=1)
1.6 Последовательная сложность алгоритма
В разделе 1.3 мы уже попытались дать некоторые оценки сложности алгоритма обучения самоорганизующейся карты Кохонена. Ниже мы рассмотрим последовательную сложность более подробно.
Прежде всего необходимо понять в терминах каких операций нам следует оценить сложность алгоритма. В алгоритме преобладают арифметические операции и операции сравнения над вещественными числами, поэтому в их терминах и будем определять сложность.
Пусть, как и ранее, N - количество объектов в обучающей выборке, L - количество нейронов в слое Кохонена, D - размерность признакового пространства объектов (размерность векторов \mathbf{x}_i) и B - количество объектов в случайной подвыборке отбираемой на каждой итерации алгоритма.
Оценим сложность одной итерации алгоритма:
- Функция ComputePairwiseDistances.
- L \times D умножений и L \times (D - 1) сложений для вычисления всех норм \left\|\mathbf{w}_j\right\|^2;
- B \times L \times D умножений и B \times L \times (D - 1) сложений для вычисления всех скалярных произведений \mathbf{x}_i^{T}\mathbf{w}_j;
- B \times L сложений для вычисления \hat{d}_{ij};
- Итого: L \times D + L \times (D - 1) + B \times L \times D + B \times L \times (D - 1) + B \times L = 2 \times L \times D \times (B + 1) - L арифметических операций над вещественными числами. Тогда асимптотическая сложность равна O(B \times L \times D);
- Функция FindClosestNeurons.
- В этой функции используются только операции сравнения между вещественными числами и их количество составляет B \times (L - 1) или асимптотически O(B \times L);
- Функция ComputeWeightedSumsAcrossObjects.
- Будем считать что для вычисления h_{b, j}(t) требуется некоторое константное число операций Const. Тогда для вычисления всех таких функций требуется B \times L \times Const операций.
- Вычисление \mathbf{w}_j делится на вычисление числителя и выисление знаменателя. В первом случае нам требуется выполнить B \times D умножений и (B - 1) \times D сложений. Во втором случае мы выполняем B сложений.
- Итого: (2 \times B \times D + B - D + 1) \times L + B \times L \times Const операций. Асимптотическая сложность: O(B \times L \times D)
В итоге асимптотическая сложность одной итерации будет составлять O(B \times L \times D).
Отметим, что не смотря на все количество операций, используя векторные и матричные операции процессора можно добится значительной эффективности.
1.7 Информационный граф
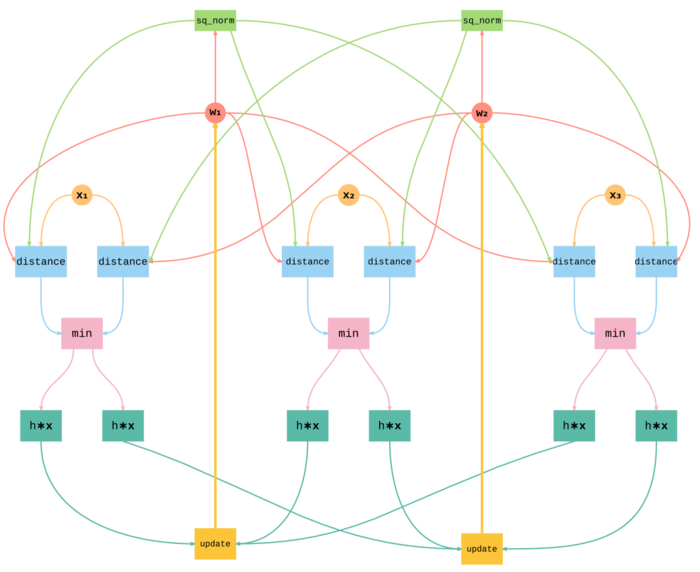
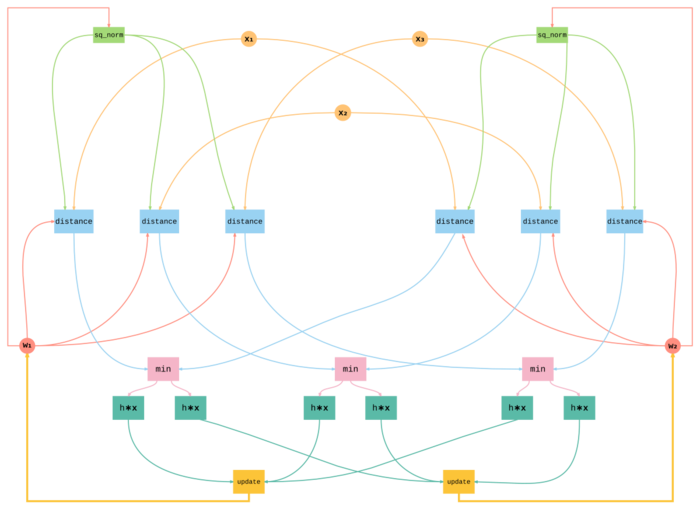
Для того чтобы сохранить простоту графа, мы выбрали максимально крупные операции, которые в тоже время хорошо показывают структуру алгоритма. Кроме того, в графе мы оперируем не на уровне отдельных компонент вектора, а на уровне целых векторов-объектов и векторов-весов и векторных операций над ними.
Нами были рассмотрены следующие операции:
- sq_norm - вычисление квадрата нормы \| \mathbf{w}_j \|^2 = \mathbf{w}_j^{T} \mathbf{w}_j
- distance - вычисления квазирасстояния между объектом и вектором весов \| \mathbf{w}_j \|^2 - 2 \mathbf{x}_i^{T} \mathbf{w}_j
- min - поиск ближайшего нейрона на основе расстояний, которые получены на входе операции
- h \ast x - вычисление веса соседства и умножения этого веса на вектор \mathbf{x} поэлементно
- update - суммирование взвешенных векторов \mathbf{x} и обновление весов нейронов
На Рис. 4 и Рис. 5 представлен информационный граф алгоритма для трех объектов \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3 и двух нейронов с весами \mathbf{w}_1, \mathbf{w}_2 в разных проекциях на плоскость.
1.8 Ресурс параллелизма алгоритма
Наиболее очевидными способами использования параллельных ресурсов для ускорения алгоритма являются:
- распределить объекты обучающей выборки по процессам (распределение данных);
- распределить веса нейронов по процессам (распределение сети);
В первом случае в каждом узле вычислительной сети мы храним часть обучающей выборки и всю нейронную сеть целиком (все веса \mathbf{w}_j), а во втором в каждом узле хранится вся обучающая выборка и некоторая подсеть исходной нейронной сети.
Допустим неограниченное количество вычислительных узлов.
Рассмотрим первый случай. Имея в своем распоряжении неограниченное количество вычислительных узлов мы можем полностью распараллелить поиск минимальных расстояний, который теперь можно сделать за O(L \times D) арифметических операций с вещественными числами. Поиск ближайшего нейрона параллельно можно сделать за O(L) сравнений. Сложность вычисления \mathbf{w}_j - O(B \times L \times D), так как нам необходима пересылка данных одному процессу, который вычислит новые значения для весов. Таким образом асимптотически мы не получили улучшения, но если рассмотреть точное количество операций при, то улучшение есть.
Рассмотрим второй случай. Расстояния мы по прежнему можем считать параллельно - O(B \times D). Но поиск минимального расстояния нужно выполнять последовательно, так как у одного рассматриваемого процесса нет расстояний до всех нейронов, поэтому сложность - O(B \times L). Сложность обновления нейронов - O(B \times D). В итоге получаем O(B \times ( L + D) ).
1.9 Входные и выходные данные алгоритма
Входными данными алгоритма являются:
- множество \mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^N - обучающая выборка. Наиболее просто можно представить обучающую выборку как матрицу \mathbf{X} \in \mathbb{R}^{N \times D}. Важно понимать, что на практике часто встречаются большие выборки состоящие из сотней тысяч объектов, каждый из которых может иметь десятки или сотни признаков (компонет), поэтомк размеры матрицы могут быть значительными;
- количество нейронов L, кроме того явно конкретизированы размеры выходной карты X, Y;
- положения нейронов на двумерной карте \mathbf{r}_j, которые мы можем упорядочить в матрицу \mathbf{R}. На самом деле задав размеры сетки и форму ячеек, мы неявно уже определили расстояния между положениями нейронов, поэтому, вообще говоря, описывать матрицу \mathbf{R} как входные данные излишне, но для ясности сделаем это;
- количество итераций T;
- начальный радиус \sigma_0.
Общая память, которая требуется нам для хранения входных данных, равна O(N \times D).
Выходными данными алгоритма являются:
- обученные веса нейронов \mathbf{w}_j, которые удобно хранить в виде матрицы \mathbf{W}.
Общая память, которая требуется нам для хранения выходных данных, равна O(L \times D).
1.10 Свойства алгоритма
Вычислительная мощность алгоритма равна O\left(\frac{BL}{N + L}\right), что при B=N равно O\left(\frac{NL}{N + L}\right), что асимптотически при большом размере выборке равно O(1).
Задача, которую решают самоогранизующиеся карты, является чрезвычайно сложной и некорректно поставленной, поэтому важной составляющей алгоритма является случайность. Она проявляется в случайном порядке выбора объектов (или случайных подмножеств объектов) для обучения. Но данное стохастическое поведение алгоритма не имеет существенного влияния на параллельную структуру алгоритма, кроме того если в batch-версии выбрать B=N, то случайность будет устранена.
Рассматрим свойства параллельной реализации. Основной проблемой реализации параллельной версии алгоритма является то, что нам необходимо выполнять массово две операции:
- искать ближайший нейрон к текущему объекту;
- обновлять веса каждого нейрона в конце итерации.
Так, если мы выполнили распределение данных, то мы имеем часть объектов, но в тоже время у нас есть локально вся сеть, следовательно найти ближайший нейрон для каждого объекта из известной нами подвыборки не требует взаимодействия с другими процессами. Но для того чтобы обновить значения весов нейронов нам необходима информация от других вычислительных узлов, в частности нам требуются h_{b(i), j} и \mathbf{x}_i, чтобы обновить веса нашей сети. Следовательно, нам необходим отдельный процесс-аггрегатор, который, получив все необходимые данные, обновил значения весов и переслал бы обновленную нейронную сеть всем остальным процессам. В целом, такой подход полностью укладывается в парадигму MapReduce.
Если же мы выбрали стратегию распределения сети, то теперь мы имеем только часть сети, но зато вся обучающая выборка. Теперь найти ближайший нейрон не так просто, так как локально мы можем проверить только те нейроны, которые хранятся в памяти процесса, поэтому остальные процессы должны переслать нам их минимальное расстояние. Далее зная номер ближайшего нейрона (при условии, что мы храним локально все положения нейронов \mathbf{R}), мы можем без труда найти выпуклую комбинацию объектов выборки и обновить веса нейронов.
Ясно, что каждый из подходов имеет свои преимущества: первый более масштабируем для выборок большого размера, когда мы физически не можем поместить все объекты в один узел, но в тоже время размеры самой нейронной сети незначительны; во втором случае мы можем строить сети состоящие из большого количества нейронов при минимальном взаимодействии процессов (процессу требуется только передать два числа - минимальное расстояние и номер нейрона, которому оно соответствует).
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
В данном разделе мы рассмотрим паралелльную реализацию алгоритма, которая основана на разделении входной выборки по всем доступным процессам. Каждый процесс работает со своим кусоком данным и в конце каждой итерации все процессы синхронизируют состояние весов нейронов. В качестве допущения мы будем рассматривать только одну итерацию алгоритма (если итераций больше чем одна, то результаты просто будут отличаться на множитель равный количеству итераций). Кроме того, допустим B = N.
Все эксперименты были выполнены на суперкомпьютере IBM Blue Gene/P. Выборка была сгенерировна из стандартного нормального распределения для N = D = 1000. Набор изменяемых параметров запуска:
- L (число нейронов с решетке) = [ 1024, 4096, 9216, 16384, 25600, 36864, 50176, 65536]
- P (число процессоров) = [ 8, 16, 32, 48, 64, 128, 384, 256, 512]
Для оценки производительности (GFLOPS) была использована оценка числа операций приведенная ранее.
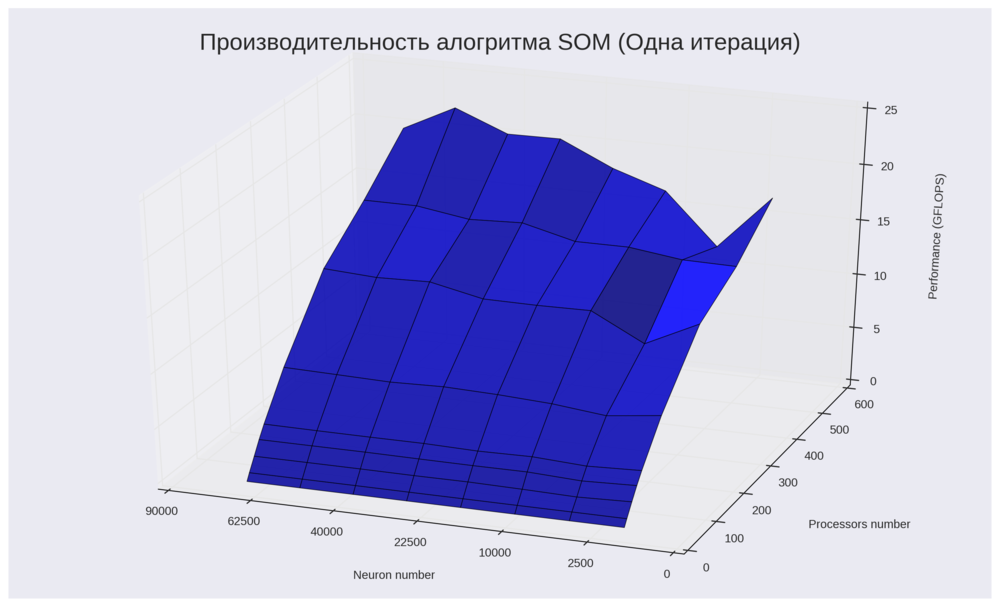
На Рис 6 показана зависимость производительности алгоритма от числа процессоров и количества нейронов в решетке. График подтверждает наше интуитивную догадку, что для больших размеров решетки алгоритм имеет большую производительность в терминах операций с плавающей точкой. Максимальная производитлеьность 24 GFLOPS достигается на 512 процессорах и для 50176 (224 * 224) нейронов. Минимальная же производительность (0.6 GFLOPS) наблюдается на 8 процессорах при любом числе нейронов.
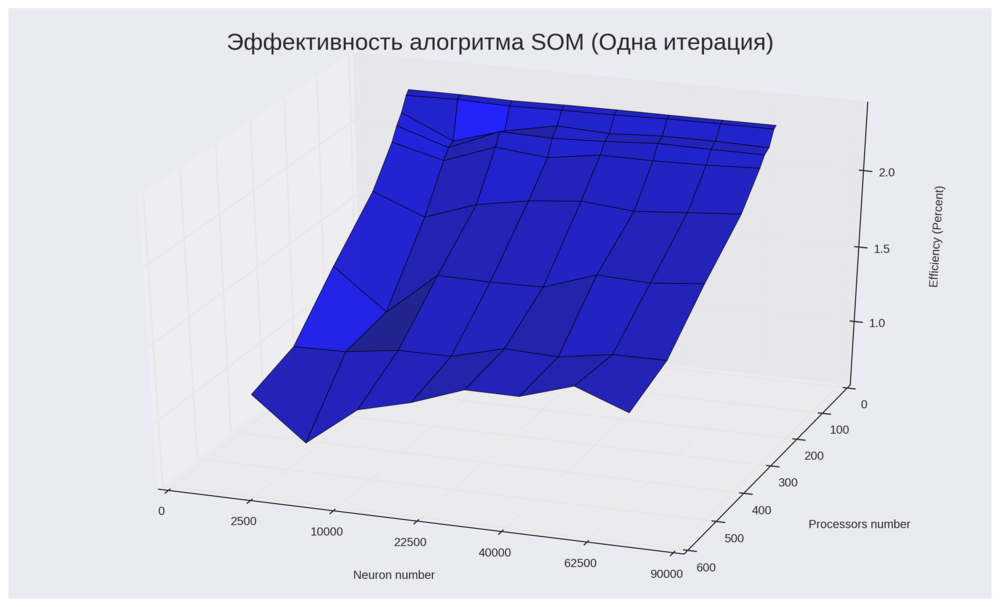
На Рис 7 показана аналогичная зависимость эффективности реализации. Здесь стоит отметить, что эффективность реализации очень низкая (в среднем 2% от пиковой производительности). Это долольно просто объяснить: в алгоритме требуется передовать больше количество данных (веса нейронов) для синхронизации процессов, поэтому значительную часть времени процессоры простаивают, ожидая передачи или отправки данных. Данная ситуация ухудшается, когда нейронов становится больше, что отлично видно на графике. Максимальная эффектвность (2.7 %) была достигнута для 8 процессов и остается неизменной при любом числе нейрнов, в данном случае более высокая эффективность достигается за счет того, что требуется осуществить синхронизацию только между 8 процессами, что намного дешевле, чем в случае 512 процессоров (минимально достигнутая эффективость - 1%).
В целом можно отметить, что алгоритм обладает свойством сильной масштабируемости: на Рис 6 можно наблюдать сублинейный рост производительности с ростом числа процессоров при фиксированном числе нейронов. Так же заметим, что алгоритм проявляет свойство слабой масштабируемости: так, например, при W / p = 128 отмечаем следующий рост производительности: [0.61, 2.17, 7.92, 21.4] при соответствующих значенияз числа процессоров: [8, 32, 128, 512]. Другой пример: W / p = 64, производительности - [1.21, 4.17, 12.96] при [16, 64, 256].
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существующие параллельные реализации:
- Somoclu: Massively parallel self-organizing maps: accelerate training on multicore CPUs, GPUs, and clusters (GNU GPLv3).
- поддержка OpenMP, MPI и CUDA;
- интерфейсы для Python, R, Julia, и Matlab
- Parallel-SOM: Parallel Implementation of Self Organzing Map in OpenCL
- MapReduce-MPI SOM: Parallel implementation of Self-Organizing Map (SOM) algorithm with MapReduce-MPI (GNU GPLv3).
Существующие последовательные реализации:
- SOM-Toolbox: A Matlab toolbox for Self-Organizing Maps (SOM) and others (GNU GPLv2).
- предоставляет инструменты для удобной визуализации полученной карты.
- MiniSom: A minimalistic implementation of the Self Organizing Maps (Creative Commons Attribution 3.0 Unported License).
- реализация на языке Python с использованием библиотеки NumPy.
- SOMPY: A Python Library for Self Organizing Map (Apache License v2).
- KNNL: C++ Kohonen Neural Network Library (BSD License).
- JKNNL: Java Kohonen Neural Network Library (BSD License).
- kohonen4j: Self-Organizing Maps in Java (GNU GPLv3).
- kohonen Supervised and Unsupervised Self-Organising Maps in R (GNU GPLv3).
3 Литература
- Teuvo Kohonen (1997). Self-Organizing Maps. Springer-Verlag New York, Inc., Secaucus, NJ, USA.
- Peter Wittek, Shi Chao Gao, Ik Soo Lim, Li Zhao (2015). Somoclu: An Efficient Parallel Library for Self-Organizing Maps. arXiv:1305.1422.
- Juha Vesanto (1999). SOM-based data visualization methods. Intell. Data Anal. 3, 2 (March 1999), 111-126.
- Timo D. Hämäläinen (2001). Parallel implementation of self-organizing maps. In Self-Organizing neural networks, Udo Seiffert and Lakhmi C. Jain (Eds.). Springer Studies In Fuzziness And Soft Computing Series, Vol. 78. Springer-Verlag New York, Inc., New York, NY, USA 245-278.
- Seung-Jin Sul, Andrey Tovchigrechko (2011). Parallelizing BLAST and SOM Algorithms with MapReduce-MPI Library. IEEE International Symposium on Parallel and Distributed Processing.