VladimirDobrovolsky611/Алгоритм SDDP: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 175: | Строка 175: | ||
l_T^k(x_{T-1}^k) = \sum_{j=1}^{m_T} \ p_{Tj}c_T^jx_t^{i_kj}+ (-\sum_{j=1}^{m_T}p_{tj}\pi_t^{i_kj}B_t^j)(x_{T-1}^{i_k} - \widehat{x}_{T-1}^{i_k}) | l_T^k(x_{T-1}^k) = \sum_{j=1}^{m_T} \ p_{Tj}c_T^jx_t^{i_kj}+ (-\sum_{j=1}^{m_T}p_{tj}\pi_t^{i_kj}B_t^j)(x_{T-1}^{i_k} - \widehat{x}_{T-1}^{i_k}) | ||
\ \ (6) | \ \ (6) | ||
| + | </math> | ||
| + | |||
| + | На этапах <math>t = 1,...,T-1</math>: | ||
| + | |||
| + | Прямые задачи: | ||
| + | |||
| + | <math> | ||
| + | Q_t(x_{t-1}^k,\xi_t^i) = | ||
| + | \left\{\begin{matrix} | ||
| + | min \ c_t^{i_k}x_t + \gamma_t | ||
| + | \\ subject \ to | ||
| + | \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}\geq b_t^{i_k} | ||
| + | \\ \gamma_t\geq l_{t+1}(x_t^{i_k}) | ||
| + | \end{matrix}\right. | ||
| + | (7) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Обратные задачи: | ||
| + | |||
| + | <math> | ||
| + | Q_t(\widehat{x}_{t-1}^k,\xi_t^i) = | ||
| + | \left\{\begin{matrix} | ||
| + | max \ \pi_T^{i_k}(\widetilde{b}_t^i - \widetilde{B}_t^i\widehat{x}_{t-1}^{i_k}) | ||
| + | \\ subject \ to | ||
| + | \\ \pi_t^{i_k}\widetilde{A}_t^{i_k}\leq \widetilde{c}_t^{i_k} | ||
| + | \end{matrix}\right. | ||
| + | (8) | ||
| + | </math> | ||
| + | |||
| + | Уравнение отсекающей гиперплоскости: | ||
| + | |||
| + | <math> | ||
| + | l_t^k(x_{t-1}^k) = \sum_{j=1}^{m_t} \ p_{tj}\widetilde{c}_t^jx_t^{i_kj}+ (-\sum_{j=1}^{m_t}p_{tj}\pi_t^{i_kj}\widetilde{B}_t^j)(x_{t-1}^{i_k} - \widehat{x}_{t-1}^{i_k}) | ||
| + | \ \ (9) | ||
</math> | </math> | ||
Версия 18:17, 6 февраля 2017
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Стохастическое двойственное динамическое программирование (SDDP) – это метод оптимизации, предназначенный для решения динамических задач в условиях неопределенности, то есть в случае, когда некоторые параметры задачи не являются детерминированными. В силу фундаментальности постановки задачи, данный алгоритм может быть применен в самых различных прикладных областях. Например, на сегодняшний день, стохастическое двойственное динамическое программирование активно используется для управления ГЭС в Норвегии, а также вводится в банках для управления рыночными рисками. На сегодняшний день также широко распространены альтернативные динамические методы поиска решений в условиях неопределенности, например, методы, работающие на принципах построения дерева возможных исходов, или методы, работающие на принципах управляющих правил. Однако, методы, работающие по принципу построения дерева, неизбежно сталкиваются с широко известным «проклятием размерности» (curse of dimensionality), а методы, построенные на принципах управляющих правил, как правило, требуют серьезные ограничения на тип управляющих правил, а также на свойства стохастических параметров задачи. Также, в задачах динамического управления присутствует проблема тайм-консистентности решения (time-consistence solution).
Алгоритм SDDP (Stochastic dual dynamic programming) впервые был предложен в статье M.V.F. Pereira и L.M.V.G. Pinto "Multi-stage stochastic optimization applied to energy planning" в 1991 году. Далее алгоритм претерпел множество модернизаций и спецификаций, описанных в труде Alexander Shapiro, Darinka Dentcheva, Andrzej Ruszczynski "Lectures on Stochastic Programming: Modeling and Theory", Теперь под аббревиатурой SDDP подразумевается целое семейство алгоритмов.
1.2 Математическое описание алгоритма
1.2.1 Постановка задачи
Исходные данные:
1. Количество этапов T, количество состояний на каждом этапе [math]m_t[/math], [math]t = 1,...,T[/math]
2. Размерность задачи N (размерность управляющего правила)
3. Вероятности переходов [math]p_{nt}; t = 1,...,T; n = 1,...,m_t[/math]
4. матрицы и векторы, характеризующие каждое состояние системы [math] \xi_i^t=(A_i^t, \ B_i^t, \ b_i^t, \ c_i^t) [/math]
Совокупность входных параметров в пунктах 1 - 4 формируют сценарную решетку задачи (см. рис. 1)
Считается, что на 1-м этапе задача детерминирована. Здесь присутствует всего одно состояние [math] \xi_1 =(A_1, \ b_1, \ c_1) [/math].
Вычисляемые данные:
Матрица управляющих действий [math]X[/math] (элементы [math]x_{it}; \ t \in 1,...,T; \ i \in 1,...,N[/math] - управления для i-го элемента на шаге t)
Постановка задачи:
[math] \left\{\begin{matrix} min \ c_1x_1 + \sum_{i=1}^{m_2}p_{1i}^1Q_2(x_1,\xi_i^2) \\subject \ to \\A_1x_1\geqslant b_1 \\x_1 \geqslant 0 \end{matrix}\right. \ \ \ (1)[/math]
где
[math] Q_t(x_{t-1},\xi_i^t) = \left\{\begin{matrix} min \ c_t^ix_t + \sum_{j=1}^{m_{t+1}}p_{ji}^tQ_{t+1}(x_t,\xi_j^{t+1}) \\subject \ to \\A_t^ix_t + B_t^ix_{t-1}\geqslant b_t^i \\x_t \geqslant 0 \end{matrix}\right. t=2,...,T-1 \ \ \ (2) [/math]
...
[math] Q_T(x_{T-1},\xi_i^T) = \left\{\begin{matrix} min \ c_T^ix_T \\subject \ to \\A_T^ix_T + B_T^ix_{T-1}\geqslant b_T^i \\x_t \geqslant 0 \end{matrix}\right. (3) [/math]
При этом функцию [math]Q_t(x_{t-1},\xi_i^t)[/math] называют функцией будущего спроса (cost-to-go function).
Данная постановка задачи позволяет решать задачи стохастического программирования, где в качестве метрики взято мат. ожидание по состояниям системы. Существуют также и другие расширения данного алгоритма, где в качестве метрики взято значение Value at Risk или Expected Shortfall, широко используемые в оценки рисков финансовых потерь.
1.2.2 Прикладная область
Существует множество прикладных задач, для которых используется данный алгоритм. далее приведены некоторые примеры:
1. Управление ГЭС
Моделируется следующая ситуация:
Существует водохранилище с ограниченным объемом воды. водохранилище наполняется за счет осадков, а опустошается с помощью шлюзов ГЭС. Также существует населенный пункт, потребляющий электроэнергию. ГЭС может генерировать электричество 2-мя способами: спускать воду из водохранилища или использовать топливные генераторы. Себестоимость электроэнергия, полученная ГЭС за счет спуска воды можно считать нулевой, в то время, как электроэнергия, выработанная за счет топливных генераторов имеет значительную себестоимость.
Считается, что количество энергии, потребляемой населенным пунктом, а также объем осадков - случайные процессы, распределения которых можно получить с помощью исторических данных. Объем водохранилища и себестоимость производства электричества тем или иным способом - известны и фиксированы. В данных условиях стоит задача минимизировать финансовые потери ГЭС на несколько лет вперед.
2. Управление портфелем ценных бумаг.
Инвестор обладает некоторым стартовым капиталом, который можно инвестировать в заданный набор ценных бумаг. Инвестор формирует финансовый портфель на несколько лет, но внутри данного периода возможны ребалансировки портфеля, проводимые, однако, без вывода и без привлечения дополнительных средств. Прирост цен активов портфеля, а также величина дивидендных выплат - случайны. При этом, транзакционные издержки, начальный капитал инвестора, а также набор возможных активов для вложения - фиксированные величины. В данных условиях стоит задача минимизировать финансовые потери инвестора.
1.2.3 Алгоритм решения
Алгоритм решения задачи (1) - (3) опирается на фундаментальное утверждение:
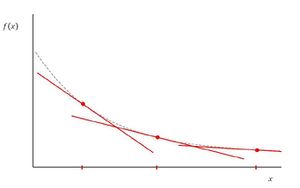
cost-to-go function, опсанная уравнением (2) является кусочно-линейной относительно аргумента [math]x_{t-1}[/math]
Данное утверждение позволяет сделать вывод, что задача (1) - (3) может быть сведена к задаче линейного программирования.
В ходе доказательства данного утверждения также показывается, что в задачу можно решить итерационно, причем каждую итерацию можно разбить на 3 этапа:
1. Инициализаци
2. Обратный ход
3. Прямой ход
На каждой итерации,в ходе прямого хода задачи достигается верхняя оценка решения, а в ходе обратного - нижняя. Причем при устремлении количества итераций к бесконечности, данные оценки сходятся к истинному решению.
1.2.3.1 Инициализация.
На данном этапе генерируются случайные сценарии на сценарной решетки задачи. Количество инициализируемых случайных сценариев может варьироваться в зависимости от структуры сетки. До сих пор не исследовано оптимальное с точки зрения скорости выполнения количество пробных сценариев и зависимость выбора этого количества от размерности решетки. Будем считать, что на каждой итерации формируется [math]K[/math] случайных сценариев, которые представляют из себя наборы состояний [math](\widehat{\xi}_{1}^{i_k},...,\widehat{\xi}_{T}^{i_k}) \ k = 1,...,K[/math]
Для каждого пробного сценария на каждом шаге решается прямая задача линейного программирования:
[math] Q_t^{i_k}(\widehat{x}_{t-1}^{k},\widehat{\xi}_{t}^{i_k}) = \left\{\begin{matrix} min \ c_t^{i_k}x_t \\ subject \ to \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}^k\geq b_t^{i_k} \end{matrix}\right. \ \ \ (2) [/math]
Получается [math]K[/math] пробных решений:
[math] \widehat{x}_t^k = \left\{\begin{matrix} argmin \ c_t^{i_k}x_t \\ subject \ to \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}^k\geq b_t^{i_k} \end{matrix}\right. [/math]
[math]k = 1,...,K[/math]
1.2.3.2 Обратный ход
На обратном ходе с помощью каждого пробного решения формируется отсекающая гиперплоскость, ограничивающая решение снизу.
Уравнение гиперплоскости получается в ходе решения прямой и обратной задач линейного программирования:
На шаге [math]T[/math]:
Прямые задачи:
[math] Q_T(\widehat{x}_{T-1}^k,\xi_T^i) = \left\{\begin{matrix} min \ c_T^{i_k}x_T \\ subject \ to \\ A_T^{i_k}x_T + B_T^{i_k}\widehat{x}_{T-1}\geq b_T^{i_k} \end{matrix}\right. (4) [/math]
Обратные задачи:
[math] Q_T(\widehat{x}_{T-1}^k,\xi_T^i) = \left\{\begin{matrix} max \ \pi_T^{i_k}(b_t^i - B_T^i\widehat{x}_{T-1}^{i_k}) \\ subject \ to \\ \pi_T^{i_k}A_T^{i_k}\leq c_T^{i_k} \end{matrix}\right. (5) [/math]
Уравнение отсекающей гиперплоскости:
[math] l_T^k(x_{T-1}^k) = \sum_{j=1}^{m_T} \ p_{Tj}c_T^jx_t^{i_kj}+ (-\sum_{j=1}^{m_T}p_{tj}\pi_t^{i_kj}B_t^j)(x_{T-1}^{i_k} - \widehat{x}_{T-1}^{i_k}) \ \ (6) [/math]
На этапах [math]t = 1,...,T-1[/math]:
Прямые задачи:
[math] Q_t(x_{t-1}^k,\xi_t^i) = \left\{\begin{matrix} min \ c_t^{i_k}x_t + \gamma_t \\ subject \ to \\ A_t^{i_k}x_t + B_t^{i_k}\widehat{x}_{t-1}\geq b_t^{i_k} \\ \gamma_t\geq l_{t+1}(x_t^{i_k}) \end{matrix}\right. (7) [/math]
Обратные задачи:
[math] Q_t(\widehat{x}_{t-1}^k,\xi_t^i) = \left\{\begin{matrix} max \ \pi_T^{i_k}(\widetilde{b}_t^i - \widetilde{B}_t^i\widehat{x}_{t-1}^{i_k}) \\ subject \ to \\ \pi_t^{i_k}\widetilde{A}_t^{i_k}\leq \widetilde{c}_t^{i_k} \end{matrix}\right. (8) [/math]
Уравнение отсекающей гиперплоскости:
[math] l_t^k(x_{t-1}^k) = \sum_{j=1}^{m_t} \ p_{tj}\widetilde{c}_t^jx_t^{i_kj}+ (-\sum_{j=1}^{m_t}p_{tj}\pi_t^{i_kj}\widetilde{B}_t^j)(x_{t-1}^{i_k} - \widehat{x}_{t-1}^{i_k}) \ \ (9) [/math]