Участник:Dmitry/Плотностный алгоритм кластеризации: различия между версиями
Dmitry (обсуждение | вклад) |
Dmitry (обсуждение | вклад) |
||
| Строка 148: | Строка 148: | ||
Было проведено исследование масштабируемости параллельной реализации алгоритма DBSCAN. Исследование проводилось на суперкомпьютере "Ломоносов". Исследовалась параллельная реализация алгоритма, написанная с использованием стандарта MPI. Распараллеливание проводилось по числу входных объектов. | Было проведено исследование масштабируемости параллельной реализации алгоритма DBSCAN. Исследование проводилось на суперкомпьютере "Ломоносов". Исследовалась параллельная реализация алгоритма, написанная с использованием стандарта MPI. Распараллеливание проводилось по числу входных объектов. | ||
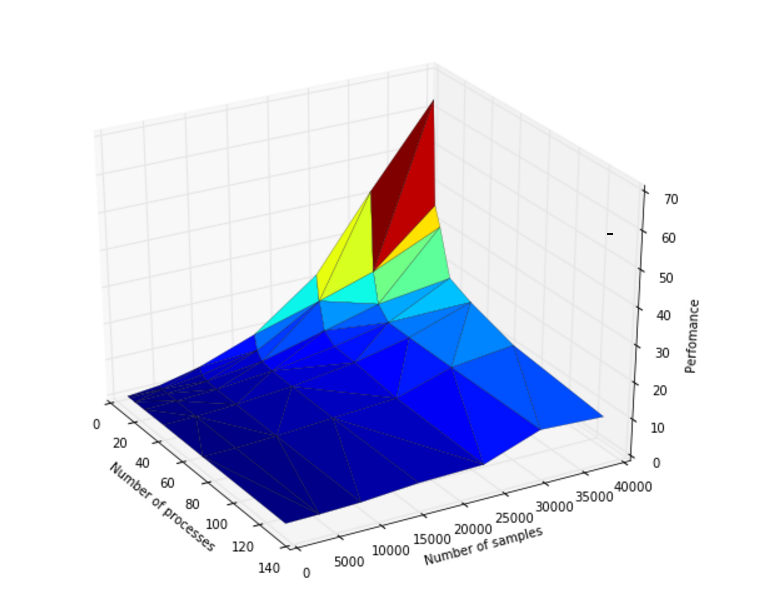
| − | [[Файл:График масштабируемости.png|thumb|center|800px|Рис. | + | [[Файл:График масштабируемости.png|thumb|center|800px|Рис. 6. График масштабируемости DBSCAN]] |
При увеличении размерности системы при фиксированном количестве процессов на области изменений значений параметров наблюдается увеличение эффективности. | При увеличении размерности системы при фиксированном количестве процессов на области изменений значений параметров наблюдается увеличение эффективности. | ||
Версия 19:47, 7 февраля 2017
| Плотностный алгоритм кластеризации DBSCAN | |
| Последовательный алгоритм | |
| Последовательная сложность | O(n \log n) |
| Объём входных данных | n |
| Объём выходных данных | n |
Авторы описания: Титов Д.Е.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Под кластеризацией понимается деление заданного множества точек данных (объектов) на подгруппы, каждая из которых, насколько это возможно, однородна. В основе метода кластеризации DBSCAN лежит объединение некоторых объектов в соответствии с их внутригрупповым «соединением». Для проведения корректной процедуры кластеризации необходимо указать критерии, по которым объекты будут объединены в кластеры. Прежде всего, необходимо сказать, что кластеры представляют собой плотные области некоторых объектов в пространстве данных, разделенных между собой объектами, плотность которых значительно ниже. Расположение точек в одном кластере обусловлено их соединением, т.е. некоторой связью между собой.
1.2 Математическое описание алгоритма
Плотность точек для данной точки X определяется двумя параметрами. Первым из них является \varepsilon – радиус «соседства» (приближенности) точки X. Тогда множество M_\varepsilon(X) будет включать в себя такие точки f_i, (i=\overline{1,n}), для которых следующее неравенство будет истинно:
[math]dist(X,f_i) \le \varepsilon[/math], [math](i=\overline{1,n})[/math]
Функция dist(var1, var2) определяет расстояние между объектами выборки D[1]. Это расстояние может вычисляться различными способами, например, как евклидово расстояние или с помощью метрики Минковского.
Вторым параметром определения плотности точек является MCP – это минимальное количество точек, которые расположены ближе всего к данной точке согласно определенному радиусу \varepsilon.
Точка f_i, (i=\overline{1,n}) будет являться окруженной точкой (согласно \varepsilon и MCP) если:
[math]M_\varepsilon(X) \ge MCP[/math]
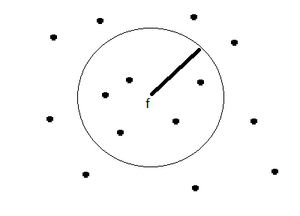
Это значит, что точка f_i, (i=\overline{1,n}) окруженная, если количество «соседствующих» точек выборки D окажется большим, либо равным значению параметра MCP (рис. 1).
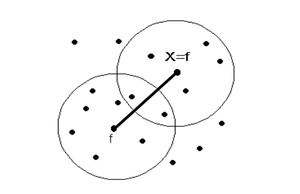
Точка X является прямо достижимой по плотности от точки f (при соответствующих \varepsilon и MCP), если точка X \in M(X), т.е. точка X – это одна из точек f для другого окружения (соседства), где f – окруженная точка (рис. 2).
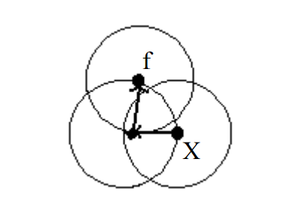
Достижимость по плотности – это транзитивное замыкание прямо достижимой по плотности точки. Точка f достижима по плотности из точки X, но точка X не достижима по плотности из точки f (рис. 3).
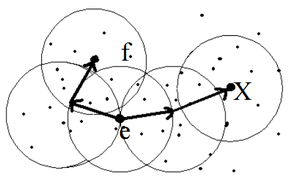
Точка X соединена (связана) по плотности с точкой f (согласно \varepsilon и MCP) если существует точка e такая, что обе точки X и f являются достижимыми от точки e (согласно \varepsilon и MCP) (рис. 4).
Кластер, сформированный на основе размещения объектов по плотности должен удовлетворять таким свойствам: максимальность; связность.
В этом случае, под кластером понимается непустое подмножество точек G из набора данных D, которое удовлетворяет вышеупомянутым свойствам, причем, максимальность интерпретируется таким образом: если X \in G и f достижима по плотности от точки X, тогда и f \in G, это значит, что обе точки принадлежат одному кластеру.
Свойство связности гласит, что каждый объект в подмножестве G соединен по плотности со всеми объектами кластера (при заданных \varepsilon и MCP).
Все объекты из набора данных D представляют собой совокупность подмножеств:
[math]D= \{ G_1, G_2,..., G_m, N \}[/math],
где G_1, G_2,..., G_m – кластеры, образованные по плотности; N – некоторое подмножество, объекты которого не принадлежат ни одному из подмножеств G_1, G_2,..., G_m.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является поиск всех "соседствующих" точек для каждой точки X входного множества D. Основное время работы алгоритма используется на функцию dist(var1, var2), определяющую расстояние между объектами выборки D и сравнение расстояния с заданной \varepsilon для того, чтобы определить "соседствующие" точки.
1.4 Макроструктура алгоритма
Основную часть алгоритма на верхнем уровне составляют множественные вычисления расстояния между объектами.
Вычисление расстояния между двумя объектами из выборки D осуществляется при помощи различных метрик. В большинстве случаев вычисляется метрика Евклида: dist(u,v)=\sqrt{(u_1-v_1)^2+(u_2-v_2)^2+...+(u_n-v_n)^2} = \sqrt{\sum_{k=1}^n(u_k-v_k)^2}.
Также возможно использование метрики Минковского, что является обобщением евклидова расстояния:
dist(x,y) = \left(\sum_{i=1}^n |x_i-y_i|^p\right)^{1/p}.
1.5 Схема реализации последовательного алгоритма
Реализация алгоритма DBSCAN может быть разделена на два этапа[2]. В первую очередь из всего набора данных D необходимо выделить те точки, которые являются окруженными. Затем выполнять следующую процедуру: для каждого объекта X из набора данных D определить:
1) принадлежит ли текущий объект к какому-нибудь из кластеров;
2) является ли текущий объект окруженной точкой.
Если текущий объект – окруженная точка, то все объекты, достижимые по плотности от текущего объекта, соединяем в новый кластер. В противном случае, если объект не является окруженной точкой и не достижим по плотности ни от какого объекта, то текущий объект – выброс. Псевдокод алгоритма DBSCAN можно представить следующим образом:
for [math]\forall X \in D[/math] [math]\{[/math] if [math] (X \in G_i, i= \overline{1,n})[/math] [math]\{[/math] if [math] (X_i \in M_\varepsilon(X))[/math] [math]\{[/math] find [math]X_i \in D[/math] достижимы по плотности from [math]X_i \in M_\varepsilon(X)[/math] [math]\}[/math] else if [math] (X_i \notin M_\varepsilon(X)[/math] and [math]X[/math] не достижим от любого другого объекта [math])[/math] [math]\{[/math] [math]X \in N[/math] [math]\}[/math] [math]\}[/math]
параметры \varepsilon и MCP задаются пользователем.
1.6 Последовательная сложность алгоритма
Сложность алгоритма зависит от поиска всех точек в \varepsilon-окрестности конкретной точки X из выборки D. Из-за поиска "соседствующих" точек алгоритм имеет квадратичную вычислительную сложность O(n^2) (где n - количество точек). Но если использовать K-мерное дерево, то можно снизить сложность до O(\text{n log n}).
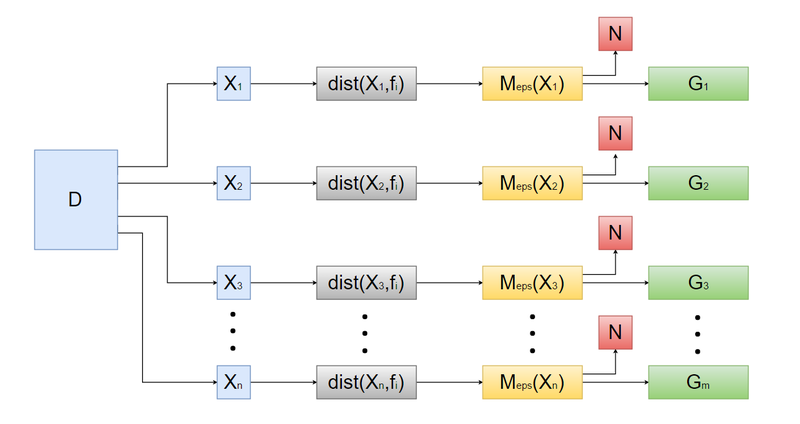
1.7 Информационный граф
Представление алгоритма DBSCAN в виде информационного графа показано на рисунке 4.
- Задаются параметры \varepsilon и MCP.
- На входе алгоритма набор данных D разбивается на множество точек X_n, где n - количество точек.
- Для каждой точки X_n из выборки D с помощью функции dist(var1, var2) определяется расстояние между остальными точками.
- Далее алгоритм объединяет точки X_n, образуя подмножества M_\varepsilon(X_n), объекты которого удовлетворяют условию: dist(X,f_i) \le \varepsilon, (i=\overline{1,n}).
- Если подмножество M_\varepsilon(X_n) состоит из MCP и больше объектов (т. е. M_\varepsilon(X_n) \ge MPC), то подмножество M_\varepsilon(X_n) образует кластер G_m.
- Подмножество N включает в себя все объекты, которые не принадлежат ни одному из подмножеств G_1, G_2,..., G_m.
1.8 Ресурс параллелизма алгоритма
Ширина ярусно-параллельной формы алгоритма O(m)[3], где m - количество частей, на которые разбиваются все объекты из набора данных D. Высотой ярусно-параллельной формы алгоритма является O(|X| \log |X|), где \mid X \mid - максимальное количество среди числа объектов в каждой части разбиения. Именно такую сложность имеет алгоритм DBSCAN, применяемый к каждой отдельной части разбиения.
1.9 Входные и выходные данные алгоритма
Входные данные: множество объектов из набора данных D, для которых задана метрическая функция расстояния dist(var1, var2). Объём входных данных: n.
Выходные данные: размеченное множество объектов, где каждому объекту сопоставлен порядковый номер кластера, в который попал данный объект, либо объект отмечается как выброс. Объём выходных данных: n.
Количество кластеров и шума в выходных данных зависят от входных данных и параметров алгоритма. Более компактное расположение объектов, меньшие значения параметра MCP, большие значения параметра \varepsilon ведут к образования меньшего числа кластеров, вплоть до одного единственного кластера. Если варьировать данные параметры в противоположную сторону, то количество кластеров и выбросов будет расти, вплоть до момента, когда все объекты будут являться выбросом.
1.10 Свойства алгоритма
- Число настраиваемых параметров равно двум: \varepsilon и MPC.
- Вычислительная сложность алгоритма O(\text{n log n}).
- Возможность обрабатывать большой объем данных.
- Результат не зависит от порядка ввода данных.
- Не требуется указывать количество кластеров.
- Возможность выделять кластеры в присутствии выбросов.
- Число итераций определено заранее[4].
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Было проведено исследование масштабируемости параллельной реализации алгоритма DBSCAN. Исследование проводилось на суперкомпьютере "Ломоносов". Исследовалась параллельная реализация алгоритма, написанная с использованием стандарта MPI. Распараллеливание проводилось по числу входных объектов.
При увеличении размерности системы при фиксированном количестве процессов на области изменений значений параметров наблюдается увеличение эффективности.
При увеличении числа процессов наблюдается уменьшение эффективности на всей области рассматриваемых значений параметров. При этом с ростом числа процессов снижение эффективности замедляется.
При одновременном увеличении количества процессов и размерности системы наблюдается уменьшение эффективности. При этом скорость убывания эффективности крайне низкая.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Scikit-Learn включает в себя реализацию Python для DBSCAN для произвольной метрики Минковского, который может быть ускорен с помощью KD-деревьев и шаровых деревьев, но который использует в худшем случае квадратичную память.
SPMF предлагает GPL-V3 java-реализацию алгоритма DBSCAN с поддержкой KD-дерева (только для параметра расстояние Евклида).
Apache Commons Мath содержит java-реализацию алгоритма выполняющегося за квадратичное время.
ELKI предлагает реализацию DBSCAN, а также GDBSCAN и другие варианты. Эта реализация может использовать различные структуры индексов для поквадратного выполнения и поддерживает произвольное расстояние функции и произвольные типы данных, но это можно обогнать низкоуровневой оптимизацией реализации на небольших наборах данных.
Weka содержит (как дополнительный пакет в последних версиях) базовую реализацию DBSCAN, которая работает за квадратичное время и линейную память.
GNU R содержит DBSCAN в fpc пакете с поддержкой произвольных функций расстояния через матриц. Однако он не имеет поддержки индекса (и, соответственно, имеет квадратичное время выполнения и сложность по памяти) и довольно медленно из-за интерпретации R. Более быстрая версия реализована на языке C++ с использованием KD-деревьев (только когда расстояние Евклидово ) в пакете R dbscan.
3 Литература
- ↑ Haykin S. Neural Networks. A Comprehensive Foun-dation. – Upper Saddle River, N.1: Prentice Hall, Inc., 1999. – 1104 с.
- ↑ Jiawei Han, Micheline Kamber. Data Mining: Con-cepts and Techniques: – Academic Press, 2001. – Р. 363-370.
- ↑ https://en.wikipedia.org/wiki/DBSCAN Density-based spatial clustering of applications with noise (DBSCAN)
- ↑ http://cyberleninka.ru/article/n/algoritmy-klasterizatsii-v-zadachah-segmentatsii-sputnikovyh-izobrazheniy