Участник:Dmitry/Плотностный алгоритм кластеризации: различия между версиями
Dmitry (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 27 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|ASA}} | ||
| + | |||
| + | {{algorithm | ||
| + | | name = Плотностный алгоритм кластеризации DBSCAN | ||
| + | | serial_complexity = <math>O(n \log n)</math> | ||
| + | | input_data = <math>n</math> | ||
| + | | output_data = <math>n</math> | ||
| + | }} | ||
Авторы описания: [[Участник:Dmitry | Титов Д.Е.]] | Авторы описания: [[Участник:Dmitry | Титов Д.Е.]] | ||
| Строка 14: | Строка 22: | ||
<math>dist(X,f_i) \le \varepsilon</math>, <math>(i=\overline{1,n})</math> | <math>dist(X,f_i) \le \varepsilon</math>, <math>(i=\overline{1,n})</math> | ||
| − | Функция <math>dist(var1, var2)</math> определяет расстояние между объектами выборки <math>D</math>. Это расстояние может вычисляться различными способами, например, как <span class="plainlinks">[//en.wikipedia.org/wiki/Euclidean_distance евклидово расстояние]</span> или с помощью <span class="plainlinks">[//en.wikipedia.org/wiki/Minkowski_distance метрики Минковского]</span>. | + | Функция <math>dist(var1, var2)</math> определяет расстояние между объектами выборки <math>D</math><ref>Haykin S. Neural Networks. A Comprehensive Foun-dation. – Upper Saddle River, N.1: Prentice Hall, Inc., 1999. – 1104 с.</ref>. Это расстояние может вычисляться различными способами, например, как <span class="plainlinks">[//en.wikipedia.org/wiki/Euclidean_distance евклидово расстояние]</span> или с помощью <span class="plainlinks">[//en.wikipedia.org/wiki/Minkowski_distance метрики Минковского]</span>. |
Вторым параметром определения плотности точек является <math>MCP</math> – это минимальное количество точек, которые расположены ближе всего к данной точке согласно определенному радиусу <math>\varepsilon</math>. | Вторым параметром определения плотности точек является <math>MCP</math> – это минимальное количество точек, которые расположены ближе всего к данной точке согласно определенному радиусу <math>\varepsilon</math>. | ||
| Строка 20: | Строка 28: | ||
Точка <math>f_i</math>, <math>(i=\overline{1,n})</math> будет являться окруженной точкой (согласно <math>\varepsilon</math> и <math>MCP</math>) если: | Точка <math>f_i</math>, <math>(i=\overline{1,n})</math> будет являться окруженной точкой (согласно <math>\varepsilon</math> и <math>MCP</math>) если: | ||
| − | <math>M_\varepsilon(X) \ | + | <math>M_\varepsilon(X) \ge MCP</math> |
Это значит, что точка <math>f_i</math>, <math>(i=\overline{1,n})</math> окруженная, если количество «соседствующих» точек выборки <math>D</math> окажется большим, либо равным значению параметра <math>MCP</math> (рис. 1). | Это значит, что точка <math>f_i</math>, <math>(i=\overline{1,n})</math> окруженная, если количество «соседствующих» точек выборки <math>D</math> окажется большим, либо равным значению параметра <math>MCP</math> (рис. 1). | ||
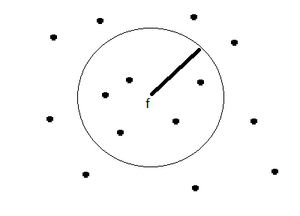
| − | [[Файл:Окруженная_точка_при_MPC_=_5.png|thumb|center|300px|Рис. 1. Окруженная точка при | + | [[Файл:Окруженная_точка_при_MPC_=_5.png|thumb|center|300px|Рис. 1. Окруженная точка при MCP = 5]] |
| − | Точка <math>X</math> является прямо достижимой по плотности от точки <math>f</math> (при соответствующих <math>\varepsilon</math> и <math> | + | Точка <math>X</math> является прямо достижимой по плотности от точки <math>f</math> (при соответствующих <math>\varepsilon</math> и <math>MCP</math>), если точка <math>X \in M(X)</math>, т.е. точка <math>X</math> – это одна из точек <math>f</math> для другого окружения (соседства), где <math>f</math> – окруженная точка (рис. 2). |
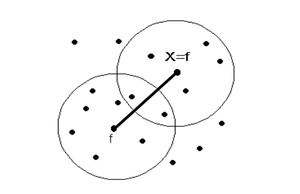
[[Файл:Точка_X_прямо_достижима_по_плотности_от_точки_f.png|thumb|center|300px|Рис. 2. Точка X прямо достижима по плотности от точки f]] | [[Файл:Точка_X_прямо_достижима_по_плотности_от_точки_f.png|thumb|center|300px|Рис. 2. Точка X прямо достижима по плотности от точки f]] | ||
| Строка 46: | Строка 54: | ||
Все объекты из набора данных <math>D</math> представляют собой совокупность подмножеств: | Все объекты из набора данных <math>D</math> представляют собой совокупность подмножеств: | ||
| − | <math>D= \{ G_1, G_2,..., | + | <math>D= \{ G_1, G_2,..., G_m, N \}</math>, |
| − | где <math>G_1, G_2,..., | + | где <math>G_1, G_2,..., G_m</math> – кластеры, образованные по плотности; <math>N</math> – некоторое подмножество, объекты которого не принадлежат ни одному из подмножеств <math>G_1, G_2,..., G_m</math>. |
== Вычислительное ядро алгоритма == | == Вычислительное ядро алгоритма == | ||
| Строка 55: | Строка 63: | ||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| + | Основную часть алгоритма на верхнем уровне составляют множественные вычисления расстояния между объектами. | ||
| + | |||
Вычисление расстояния между двумя объектами из выборки <math>D</math> осуществляется при помощи различных метрик. В большинстве случаев вычисляется метрика Евклида: <math>dist(u,v)=\sqrt{(u_1-v_1)^2+(u_2-v_2)^2+...+(u_n-v_n)^2} = \sqrt{\sum_{k=1}^n(u_k-v_k)^2}.</math> | Вычисление расстояния между двумя объектами из выборки <math>D</math> осуществляется при помощи различных метрик. В большинстве случаев вычисляется метрика Евклида: <math>dist(u,v)=\sqrt{(u_1-v_1)^2+(u_2-v_2)^2+...+(u_n-v_n)^2} = \sqrt{\sum_{k=1}^n(u_k-v_k)^2}.</math> | ||
| Строка 62: | Строка 72: | ||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| + | |||
| + | Реализация алгоритма DBSCAN может быть разделена на два этапа<ref>Jiawei Han, Micheline Kamber. Data Mining: Con-cepts and Techniques: – Academic Press, 2001. – Р. 363-370.</ref>. В первую очередь из всего набора данных <math>D</math> необходимо выделить те точки, которые являются окруженными. Затем выполнять следующую процедуру: для каждого объекта <math>X</math> из набора данных <math>D</math> определить: | ||
| + | |||
| + | 1) принадлежит ли текущий объект к какому-нибудь из кластеров; | ||
| + | |||
| + | 2) является ли текущий объект окруженной точкой. | ||
| + | |||
| + | Если текущий объект – окруженная точка, то все объекты, достижимые по плотности от текущего объекта, соединяем в новый кластер. В противном случае, если объект не является окруженной точкой и не достижим по плотности ни от какого объекта, то текущий объект – выброс. Псевдокод алгоритма DBSCAN можно представить следующим образом: | ||
| + | |||
| + | for <math>\forall X \in D</math> | ||
| + | <math>\{</math> | ||
| + | if <math> (X \in G_i, i= \overline{1,n})</math> | ||
| + | <math>\{</math> | ||
| + | if <math> (X_i \in M_\varepsilon(X))</math> | ||
| + | <math>\{</math> | ||
| + | find <math>X_i \in D</math> достижимы по плотности | ||
| + | from <math>X_i \in M_\varepsilon(X)</math> | ||
| + | <math>\}</math> | ||
| + | else if <math> (X_i \notin M_\varepsilon(X)</math> and <math>X</math> не достижим от любого другого объекта <math>)</math> | ||
| + | <math>\{</math> | ||
| + | <math>X \in N</math> | ||
| + | <math>\}</math> | ||
| + | <math>\}</math> | ||
| + | |||
| + | параметры <math>\varepsilon</math> и <math>MCP</math> задаются пользователем. | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| + | |||
| + | Сложность алгоритма зависит от поиска всех точек в <math>\varepsilon</math>-окрестности конкретной точки <math>X</math> из выборки <math>D</math>. Из-за поиска "соседствующих" точек алгоритм имеет квадратичную вычислительную сложность <math>O(n^2)</math> (где n - количество точек). Но если использовать K-мерное дерево, то можно снизить сложность до <math>O(\text{n log n})</math>. | ||
== Информационный граф == | == Информационный граф == | ||
| + | |||
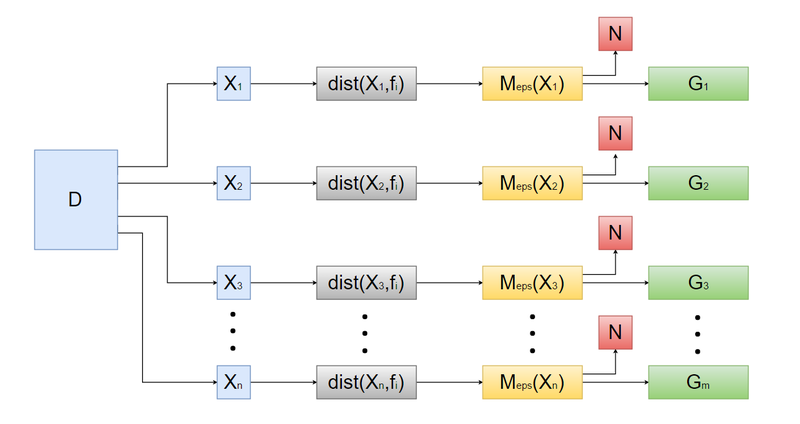
| + | Представление алгоритма DBSCAN в виде информационного графа показано на рисунке 4. | ||
| + | |||
| + | * Задаются параметры <math>\varepsilon</math> и <math>MCP</math>. | ||
| + | * На входе алгоритма набор данных <math>D</math> разбивается на множество точек <math>X_n</math>, где <math>n</math> - количество точек. | ||
| + | * Для каждой точки <math>X_n</math> из выборки <math>D</math> с помощью функции <math>dist(var1, var2)</math> определяется расстояние между остальными точками. | ||
| + | * Далее алгоритм объединяет точки <math>X_n</math>, образуя подмножества <math>M_\varepsilon(X_n)</math>, объекты которого удовлетворяют условию: <math>dist(X,f_i) \le \varepsilon</math>, <math>(i=\overline{1,n})</math>. | ||
| + | * Если подмножество <math>M_\varepsilon(X_n)</math> состоит из <math>MCP</math> и больше объектов (т. е. <math>M_\varepsilon(X_n) \ge MPC</math>), то подмножество <math>M_\varepsilon(X_n)</math> образует кластер <math>G_m</math>. | ||
| + | * Подмножество <math>N</math> включает в себя все объекты, которые не принадлежат ни одному из подмножеств <math>G_1, G_2,..., G_m</math>. | ||
| + | |||
| + | |||
| + | [[Файл:DBSCAN.png|thumb|center|800px|Рис. 5. Информационный граф алгоритма DBSCAN]] | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| + | |||
| + | Ширина ярусно-параллельной формы алгоритма <math>O(m)</math><ref>https://en.wikipedia.org/wiki/DBSCAN Density-based spatial clustering of applications with noise (DBSCAN)</ref>, где m - количество частей, на которые разбиваются все объекты из набора данных <math>D</math>. Высотой ярусно-параллельной формы алгоритма является <math>O(|X| \log |X|)</math>, где <math>\mid X \mid</math> - максимальное количество среди числа объектов в каждой части разбиения. Именно такую сложность имеет алгоритм DBSCAN, применяемый к каждой отдельной части разбиения. | ||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| + | |||
| + | Входные данные: множество объектов из набора данных <math>D</math>, для которых задана метрическая функция расстояния <math>dist(var1, var2)</math>. Объём входных данных: <math>n</math>. | ||
| + | |||
| + | Выходные данные: размеченное множество объектов, где каждому объекту сопоставлен порядковый номер кластера, в который попал данный объект, либо объект отмечается как выброс. Объём выходных данных: <math>n</math>. | ||
| + | |||
| + | Количество кластеров и шума в выходных данных зависят от входных данных и параметров алгоритма. Более компактное расположение объектов, меньшие значения параметра <math>MCP</math>, большие значения параметра <math>\varepsilon</math> ведут к образования меньшего числа кластеров, вплоть до одного единственного кластера. Если варьировать данные параметры в противоположную сторону, то количество кластеров и выбросов будет расти, вплоть до момента, когда все объекты будут являться выбросом. | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| + | |||
| + | * Число настраиваемых параметров равно двум: <math>\varepsilon</math> и <math>MPC</math>. | ||
| + | * Вычислительная сложность алгоритма <math>O(\text{n log n})</math>. | ||
| + | * Возможность обрабатывать большой объем данных. | ||
| + | * Результат не зависит от порядка ввода данных. | ||
| + | * Не требуется указывать количество кластеров. | ||
| + | * Возможность выделять кластеры в присутствии выбросов. | ||
| + | * Число итераций определено заранее<ref>http://cyberleninka.ru/article/n/algoritmy-klasterizatsii-v-zadachah-segmentatsii-sputnikovyh-izobrazheniy</ref>. | ||
= Программная реализация алгоритма = | = Программная реализация алгоритма = | ||
| Строка 82: | Строка 147: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | |||
| + | Было проведено исследование масштабируемости параллельной реализации алгоритма DBSCAN. Исследование проводилось на суперкомпьютере "Ломоносов". Исследовалась параллельная реализация алгоритма, написанная с использованием стандарта MPI. Распараллеливание проводилось по числу входных объектов. Программа реализована на языке C++. | ||
| + | |||
| + | Набор и границы значений изменяемых параметров запуска реализации алгоритма: | ||
| + | |||
| + | * число процессоров [1 : 128] с шагом по степеням двойки; | ||
| + | * число входных объектов [1000 : 40000]. | ||
| + | |||
| + | |||
| + | [[Файл:График масштабируемостиv2.png|thumb|center|800px|Рис. 6. График масштабируемости DBSCAN]] | ||
| + | |||
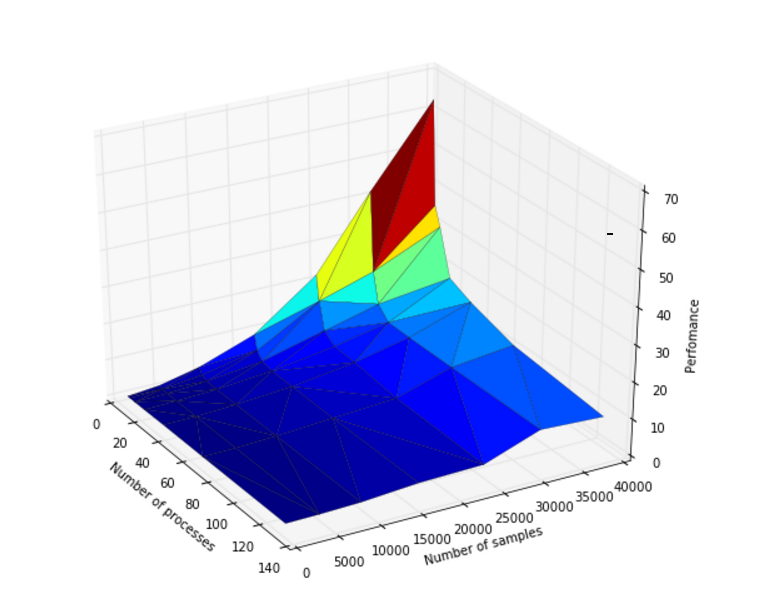
| + | На рисунке 6 показан график масштабируемости DBSCAN, из которого можно сделать следующие выводы: | ||
| + | |||
| + | * При увеличении размерности системы при фиксированном количестве процессов на области изменений значений параметров наблюдается увеличение эффективности. | ||
| + | |||
| + | * При увеличении числа процессов наблюдается уменьшение эффективности на всей области рассматриваемых значений параметров. При этом с ростом числа процессов снижение эффективности замедляется. | ||
| + | |||
| + | * При одновременном увеличении количества процессов и размерности системы наблюдается уменьшение эффективности. При этом скорость убывания эффективности крайне низкая. | ||
| + | |||
| + | [https://github.com/ByDmitryT/DBSCAN Реализация на языке C++] | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
| Строка 88: | Строка 173: | ||
== Существующие реализации алгоритма == | == Существующие реализации алгоритма == | ||
| + | |||
| + | <span class="plainlinks">[//en.wikipedia.org/wiki/Scikit-learn Scikit-Learn]</span> включает в себя реализацию Python для DBSCAN для произвольной метрики Минковского, который может быть ускорен с помощью KD-деревьев и шаровых деревьев, но который использует в худшем случае квадратичную память. | ||
| + | |||
| + | [//www.philippe-fournier-viger.com/spmf/SPMF SPMF] предлагает GPL-V3 java-реализацию алгоритма DBSCAN с поддержкой KD-дерева (только для параметра расстояние Евклида). | ||
| + | |||
| + | <span class="plainlinks">[//en.wikipedia.org/wiki/Apache_Commons Apache Commons Мath]</span> содержит java-реализацию алгоритма выполняющегося за квадратичное время. | ||
| + | |||
| + | <span class="plainlinks">[//en.wikipedia.org/wiki/ELKI ELKI]</span> предлагает реализацию DBSCAN, а также GDBSCAN и другие варианты. Эта реализация может использовать различные структуры индексов для поквадратного выполнения и поддерживает произвольное расстояние функции и произвольные типы данных, но это можно обогнать низкоуровневой оптимизацией реализации на небольших наборах данных. | ||
| + | |||
| + | <span class="plainlinks">[//en.wikipedia.org/wiki/Weka_(machine_learning) Weka]</span> содержит (как дополнительный пакет в последних версиях) базовую реализацию DBSCAN, которая работает за квадратичное время и линейную память. | ||
| + | |||
| + | <span class="plainlinks">[//en.wikipedia.org/wiki/R_(programming_language) GNU R]</span> содержит DBSCAN в [//cran.r-project.org/web/packages/fpc/index.html fpc] пакете с поддержкой произвольных функций расстояния через матриц. Однако он не имеет поддержки индекса (и, соответственно, имеет квадратичное время выполнения и сложность по памяти) и довольно медленно из-за интерпретации R. Более быстрая версия реализована на языке C++ с использованием KD-деревьев (только когда расстояние Евклидово ) в пакете R [//cran.r-project.org/web/packages/dbscan/index.html dbscan]. | ||
= Литература = | = Литература = | ||
Текущая версия на 10:11, 9 февраля 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 09.02.2017 Данная работа соответствует формальным критериям. Проверено ASA. |
| Плотностный алгоритм кластеризации DBSCAN | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n \log n)[/math] |
| Объём входных данных | [math]n[/math] |
| Объём выходных данных | [math]n[/math] |
Авторы описания: Титов Д.Е.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Под кластеризацией понимается деление заданного множества точек данных (объектов) на подгруппы, каждая из которых, насколько это возможно, однородна. В основе метода кластеризации DBSCAN лежит объединение некоторых объектов в соответствии с их внутригрупповым «соединением». Для проведения корректной процедуры кластеризации необходимо указать критерии, по которым объекты будут объединены в кластеры. Прежде всего, необходимо сказать, что кластеры представляют собой плотные области некоторых объектов в пространстве данных, разделенных между собой объектами, плотность которых значительно ниже. Расположение точек в одном кластере обусловлено их соединением, т.е. некоторой связью между собой.
1.2 Математическое описание алгоритма
Плотность точек для данной точки [math]X[/math] определяется двумя параметрами. Первым из них является [math]\varepsilon[/math] – радиус «соседства» (приближенности) точки [math]X[/math]. Тогда множество [math]M_\varepsilon(X)[/math] будет включать в себя такие точки [math]f_i[/math], [math](i=\overline{1,n})[/math], для которых следующее неравенство будет истинно:
[math]dist(X,f_i) \le \varepsilon[/math], [math](i=\overline{1,n})[/math]
Функция [math]dist(var1, var2)[/math] определяет расстояние между объектами выборки [math]D[/math][1]. Это расстояние может вычисляться различными способами, например, как евклидово расстояние или с помощью метрики Минковского.
Вторым параметром определения плотности точек является [math]MCP[/math] – это минимальное количество точек, которые расположены ближе всего к данной точке согласно определенному радиусу [math]\varepsilon[/math].
Точка [math]f_i[/math], [math](i=\overline{1,n})[/math] будет являться окруженной точкой (согласно [math]\varepsilon[/math] и [math]MCP[/math]) если:
[math]M_\varepsilon(X) \ge MCP[/math]
Это значит, что точка [math]f_i[/math], [math](i=\overline{1,n})[/math] окруженная, если количество «соседствующих» точек выборки [math]D[/math] окажется большим, либо равным значению параметра [math]MCP[/math] (рис. 1).
Точка [math]X[/math] является прямо достижимой по плотности от точки [math]f[/math] (при соответствующих [math]\varepsilon[/math] и [math]MCP[/math]), если точка [math]X \in M(X)[/math], т.е. точка [math]X[/math] – это одна из точек [math]f[/math] для другого окружения (соседства), где [math]f[/math] – окруженная точка (рис. 2).
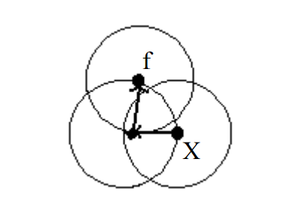
Достижимость по плотности – это транзитивное замыкание прямо достижимой по плотности точки. Точка [math]f[/math] достижима по плотности из точки [math]X[/math], но точка [math]X[/math] не достижима по плотности из точки [math]f[/math] (рис. 3).
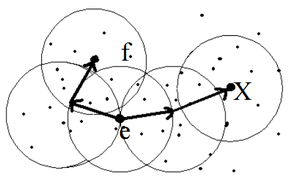
Точка [math]X[/math] соединена (связана) по плотности с точкой [math]f[/math] (согласно [math]\varepsilon[/math] и [math]MCP[/math]) если существует точка [math]e[/math] такая, что обе точки [math]X[/math] и [math]f[/math] являются достижимыми от точки [math]e[/math] (согласно [math]\varepsilon[/math] и [math]MCP[/math]) (рис. 4).
Кластер, сформированный на основе размещения объектов по плотности должен удовлетворять таким свойствам: максимальность; связность.
В этом случае, под кластером понимается непустое подмножество точек [math]G[/math] из набора данных [math]D[/math], которое удовлетворяет вышеупомянутым свойствам, причем, максимальность интерпретируется таким образом: если [math]X \in G[/math] и [math]f[/math] достижима по плотности от точки [math]X[/math], тогда и [math]f \in G[/math], это значит, что обе точки принадлежат одному кластеру.
Свойство связности гласит, что каждый объект в подмножестве [math]G[/math] соединен по плотности со всеми объектами кластера (при заданных [math]\varepsilon[/math] и [math]MCP[/math]).
Все объекты из набора данных [math]D[/math] представляют собой совокупность подмножеств:
[math]D= \{ G_1, G_2,..., G_m, N \}[/math],
где [math]G_1, G_2,..., G_m[/math] – кластеры, образованные по плотности; [math]N[/math] – некоторое подмножество, объекты которого не принадлежат ни одному из подмножеств [math]G_1, G_2,..., G_m[/math].
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является поиск всех "соседствующих" точек для каждой точки [math]X[/math] входного множества [math]D[/math]. Основное время работы алгоритма используется на функцию [math]dist(var1, var2)[/math], определяющую расстояние между объектами выборки [math]D[/math] и сравнение расстояния с заданной [math]\varepsilon[/math] для того, чтобы определить "соседствующие" точки.
1.4 Макроструктура алгоритма
Основную часть алгоритма на верхнем уровне составляют множественные вычисления расстояния между объектами.
Вычисление расстояния между двумя объектами из выборки [math]D[/math] осуществляется при помощи различных метрик. В большинстве случаев вычисляется метрика Евклида: [math]dist(u,v)=\sqrt{(u_1-v_1)^2+(u_2-v_2)^2+...+(u_n-v_n)^2} = \sqrt{\sum_{k=1}^n(u_k-v_k)^2}.[/math]
Также возможно использование метрики Минковского, что является обобщением евклидова расстояния:
[math]dist(x,y) = \left(\sum_{i=1}^n |x_i-y_i|^p\right)^{1/p}[/math].
1.5 Схема реализации последовательного алгоритма
Реализация алгоритма DBSCAN может быть разделена на два этапа[2]. В первую очередь из всего набора данных [math]D[/math] необходимо выделить те точки, которые являются окруженными. Затем выполнять следующую процедуру: для каждого объекта [math]X[/math] из набора данных [math]D[/math] определить:
1) принадлежит ли текущий объект к какому-нибудь из кластеров;
2) является ли текущий объект окруженной точкой.
Если текущий объект – окруженная точка, то все объекты, достижимые по плотности от текущего объекта, соединяем в новый кластер. В противном случае, если объект не является окруженной точкой и не достижим по плотности ни от какого объекта, то текущий объект – выброс. Псевдокод алгоритма DBSCAN можно представить следующим образом:
for [math]\forall X \in D[/math] [math]\{[/math] if [math] (X \in G_i, i= \overline{1,n})[/math] [math]\{[/math] if [math] (X_i \in M_\varepsilon(X))[/math] [math]\{[/math] find [math]X_i \in D[/math] достижимы по плотности from [math]X_i \in M_\varepsilon(X)[/math] [math]\}[/math] else if [math] (X_i \notin M_\varepsilon(X)[/math] and [math]X[/math] не достижим от любого другого объекта [math])[/math] [math]\{[/math] [math]X \in N[/math] [math]\}[/math] [math]\}[/math]
параметры [math]\varepsilon[/math] и [math]MCP[/math] задаются пользователем.
1.6 Последовательная сложность алгоритма
Сложность алгоритма зависит от поиска всех точек в [math]\varepsilon[/math]-окрестности конкретной точки [math]X[/math] из выборки [math]D[/math]. Из-за поиска "соседствующих" точек алгоритм имеет квадратичную вычислительную сложность [math]O(n^2)[/math] (где n - количество точек). Но если использовать K-мерное дерево, то можно снизить сложность до [math]O(\text{n log n})[/math].
1.7 Информационный граф
Представление алгоритма DBSCAN в виде информационного графа показано на рисунке 4.
- Задаются параметры [math]\varepsilon[/math] и [math]MCP[/math].
- На входе алгоритма набор данных [math]D[/math] разбивается на множество точек [math]X_n[/math], где [math]n[/math] - количество точек.
- Для каждой точки [math]X_n[/math] из выборки [math]D[/math] с помощью функции [math]dist(var1, var2)[/math] определяется расстояние между остальными точками.
- Далее алгоритм объединяет точки [math]X_n[/math], образуя подмножества [math]M_\varepsilon(X_n)[/math], объекты которого удовлетворяют условию: [math]dist(X,f_i) \le \varepsilon[/math], [math](i=\overline{1,n})[/math].
- Если подмножество [math]M_\varepsilon(X_n)[/math] состоит из [math]MCP[/math] и больше объектов (т. е. [math]M_\varepsilon(X_n) \ge MPC[/math]), то подмножество [math]M_\varepsilon(X_n)[/math] образует кластер [math]G_m[/math].
- Подмножество [math]N[/math] включает в себя все объекты, которые не принадлежат ни одному из подмножеств [math]G_1, G_2,..., G_m[/math].
1.8 Ресурс параллелизма алгоритма
Ширина ярусно-параллельной формы алгоритма [math]O(m)[/math][3], где m - количество частей, на которые разбиваются все объекты из набора данных [math]D[/math]. Высотой ярусно-параллельной формы алгоритма является [math]O(|X| \log |X|)[/math], где [math]\mid X \mid[/math] - максимальное количество среди числа объектов в каждой части разбиения. Именно такую сложность имеет алгоритм DBSCAN, применяемый к каждой отдельной части разбиения.
1.9 Входные и выходные данные алгоритма
Входные данные: множество объектов из набора данных [math]D[/math], для которых задана метрическая функция расстояния [math]dist(var1, var2)[/math]. Объём входных данных: [math]n[/math].
Выходные данные: размеченное множество объектов, где каждому объекту сопоставлен порядковый номер кластера, в который попал данный объект, либо объект отмечается как выброс. Объём выходных данных: [math]n[/math].
Количество кластеров и шума в выходных данных зависят от входных данных и параметров алгоритма. Более компактное расположение объектов, меньшие значения параметра [math]MCP[/math], большие значения параметра [math]\varepsilon[/math] ведут к образования меньшего числа кластеров, вплоть до одного единственного кластера. Если варьировать данные параметры в противоположную сторону, то количество кластеров и выбросов будет расти, вплоть до момента, когда все объекты будут являться выбросом.
1.10 Свойства алгоритма
- Число настраиваемых параметров равно двум: [math]\varepsilon[/math] и [math]MPC[/math].
- Вычислительная сложность алгоритма [math]O(\text{n log n})[/math].
- Возможность обрабатывать большой объем данных.
- Результат не зависит от порядка ввода данных.
- Не требуется указывать количество кластеров.
- Возможность выделять кластеры в присутствии выбросов.
- Число итераций определено заранее[4].
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Было проведено исследование масштабируемости параллельной реализации алгоритма DBSCAN. Исследование проводилось на суперкомпьютере "Ломоносов". Исследовалась параллельная реализация алгоритма, написанная с использованием стандарта MPI. Распараллеливание проводилось по числу входных объектов. Программа реализована на языке C++.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [1 : 128] с шагом по степеням двойки;
- число входных объектов [1000 : 40000].
На рисунке 6 показан график масштабируемости DBSCAN, из которого можно сделать следующие выводы:
- При увеличении размерности системы при фиксированном количестве процессов на области изменений значений параметров наблюдается увеличение эффективности.
- При увеличении числа процессов наблюдается уменьшение эффективности на всей области рассматриваемых значений параметров. При этом с ростом числа процессов снижение эффективности замедляется.
- При одновременном увеличении количества процессов и размерности системы наблюдается уменьшение эффективности. При этом скорость убывания эффективности крайне низкая.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Scikit-Learn включает в себя реализацию Python для DBSCAN для произвольной метрики Минковского, который может быть ускорен с помощью KD-деревьев и шаровых деревьев, но который использует в худшем случае квадратичную память.
SPMF предлагает GPL-V3 java-реализацию алгоритма DBSCAN с поддержкой KD-дерева (только для параметра расстояние Евклида).
Apache Commons Мath содержит java-реализацию алгоритма выполняющегося за квадратичное время.
ELKI предлагает реализацию DBSCAN, а также GDBSCAN и другие варианты. Эта реализация может использовать различные структуры индексов для поквадратного выполнения и поддерживает произвольное расстояние функции и произвольные типы данных, но это можно обогнать низкоуровневой оптимизацией реализации на небольших наборах данных.
Weka содержит (как дополнительный пакет в последних версиях) базовую реализацию DBSCAN, которая работает за квадратичное время и линейную память.
GNU R содержит DBSCAN в fpc пакете с поддержкой произвольных функций расстояния через матриц. Однако он не имеет поддержки индекса (и, соответственно, имеет квадратичное время выполнения и сложность по памяти) и довольно медленно из-за интерпретации R. Более быстрая версия реализована на языке C++ с использованием KD-деревьев (только когда расстояние Евклидово ) в пакете R dbscan.
3 Литература
- ↑ Haykin S. Neural Networks. A Comprehensive Foun-dation. – Upper Saddle River, N.1: Prentice Hall, Inc., 1999. – 1104 с.
- ↑ Jiawei Han, Micheline Kamber. Data Mining: Con-cepts and Techniques: – Academic Press, 2001. – Р. 363-370.
- ↑ https://en.wikipedia.org/wiki/DBSCAN Density-based spatial clustering of applications with noise (DBSCAN)
- ↑ http://cyberleninka.ru/article/n/algoritmy-klasterizatsii-v-zadachah-segmentatsii-sputnikovyh-izobrazheniy