Участник:Jhuighuy/Уравнение Пуассона, решение методом Галеркина: различия между версиями
Jhuighuy (обсуждение | вклад) |
Jhuighuy (обсуждение | вклад) |
||
| Строка 140: | Строка 140: | ||
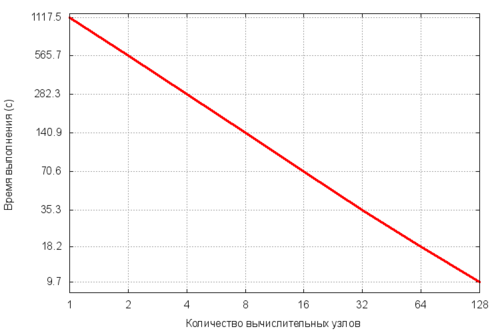
[[Файл:GalerkinMPI_Perf.png|thumb|center|500px|Рисунок 2. Оценка сильной масштабируемости метода Галеркина.]] | [[Файл:GalerkinMPI_Perf.png|thumb|center|500px|Рисунок 2. Оценка сильной масштабируемости метода Галеркина.]] | ||
| − | Анализируя график, видно, что производительность растет линейно с увеличением количества вычислительных узлов. Шкала на данном графике логарифмическая. | + | Анализируя график, видно, что производительность растет линейно с увеличением количества вычислительных узлов. Шкала на данном графике логарифмическая. Это можно объяснить отсутствием расходом на обмен данными между процессами при вычислении коэффициентов приближенного решения и значений функции. |
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
Версия 18:02, 29 ноября 2017
Уравнение Пуассона, решение методом Галеркина, Бутаков О.Б.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Галеркина (Галеркина-Бубнова) метод решения краевых задач для дифференциальных уравнений. В данной статье рассмотрим алгоритм метода Галеркина для решения уравнения Пуассона с краевыми условиями первого рода:
- [math] \newcommand{\laplace}{\mathop{}\!\mathbin\bigtriangleup} \begin{cases} \laplace u = -f, u = \phi(x,y,z), (x,y,z) \in G, G = (0,L_x)\times(0,L_y)\times(0,L_z), \\ u(x,y,z) = 0, (x,y,z) \in \partial G. \end{cases} [/math]
Алгоритм предполагает выбор полного набора базисных функций, удовлетворяющих краевым условиям. Решение строится в виде линейной комбинации базисных функций, коэффициенты находятся исходя из ортогональности невязки базисной фукнции.
1.2 Математическое описание алгоритма
Выберем тригонометрическую систему базисных функций:
- [math] \phi_{m,n,l} = sin(\frac{\pi m x}{L_x})sin(\frac{\pi n y}{L_y})sin(\frac{\pi l z}{L_z}), m=1..N_x, n=1..N_y, l=1..N_z. [/math]
Очевидно, эта система удовлетворяет краевым условиям. Проверим ортогональность функций, введя скалярное произведение [math](u,v) = \int_{0}^{L_x}\int_{0}^{L_y}\int_{0}^{L_z} u v dx dy dz[/math]:
- [math] (\phi_{m,n,l} \phi_{i,j,k}) = \int_{0}^{L_x}\int_{0}^{L_y}\int_{0}^{L_z} \phi_{m,n,l} \phi_{i,j,k} dx dy dz = \int_{0}^{L_x} sin(\frac{\pi m x}{L_x}) sin(\frac{\pi i x}{L_x}) dx \int_{0}^{L_y} sin(\frac{\pi n x}{L_y}) sin(\frac{\pi j x}{L_y}) dy \int_{0}^{L_z} sin(\frac{\pi l x}{L_z}) sin(\frac{\pi k x}{L_z}) dz = \delta_{m,i}\frac{L_x}{2} \delta_{n,j}\frac{L_y}{2} \delta_{l,k}\frac{L_z}{2}. [/math]
Выражение выше, с учетом известной ортогональности тригонометрического ряда, дает выражение для нормы, которое потребуется в дальнейшем.
Представим приближенное решение в виде комбинации базисных функций:
- [math] \hat{u} = \Sigma_{m,n,l=1}^{L_x,L_y,L_z} C_{m,n,l} \phi_{m,n,l} [/math].
Подставим выражение для приближенного решения в уравнение, получим выражение для невязки:
- [math] R(x,y,z) = \laplace\hat{u} + f = -\Sigma_{m,n,l=1}^{N_x,N_y,N_z} C_{m,n,l} \pi^2(\frac{m^2}{L_x^2}+\frac{n^2}{L_y^2}+\frac{l^2}{L_z^2}) \phi_{m,n,l} + f [/math].
Разложив выражение для невязки, потребуем ортогональность невязки базисным функциям:
- [math] \begin{split} &R_{i,j,k} = (R, \phi_{i,j,k}) = -C_{i,j,k} \pi^2(\frac{m^2}{L_x^2}+\frac{n^2}{L_y^2}+\frac{l^2}{L_z^2}) \frac{L_x}{2}\frac{L_y}{2}\frac{L_z}{2} + (f, \phi_{i,j,k}) = 0 \Rightarrow \\ &C_{i,j,k} = \frac{8 L_x L_y L_z (f, \phi_{i,j,k})}{\pi^2 ((i L_y L_z)^2 + (j L_x L_z)^2 + (k L_x L_y)^2)}, i=1..N_x, j=1..N_y. k=1..N_z. \end{split} [/math].
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из вычисления интегралов для нахождения коэффициентов приближенного решения, а также нахождение приближенного решения на сетке. Опишем сетку:
- [math] \omega_h = [(x_i,y_j,z_k); x_i=i\Delta x, y_j=i\Delta y, z_k=k\Delta k; L_x=M_x\Delta x, L_y=M_y\Delta y, L_z=M_z\Delta z]. [/math]
Тогда трехмерный интеграл будет приближенно описываться выражением:
- [math] \int_{0}^{L_x}\int_{0}^{L_y}\int_{0}^{L_z} f dx dy dz \approx \Sigma_{m,n,l=1}^{M_x,M_y,M_z} f(x_i,y_j,z_k)\Delta x\Delta y\Delta z. [/math]
Вычисление функции на сетке тривиально:
- [math] \hat{u}_{h,i,j,k} = \Sigma_{m,n,l=1}^{N_x,N_y,N_z} C_{m,n,l} sin(\frac{\pi m x_i}{L_x})sin(\frac{\pi n y_j}{L_y})sin(\frac{\pi l z_k}{L_z}). [/math]
1.4 Макроструктура алгоритма
Рассмотрим две возможные структуры алгоритма, в одной сначала вычислим все коэффициенты, а потом восстановим функцию. Алгоритм:
- Для всех [math]i=1..N_x, j=1..N_y, k=1..N_z[/math] вычислить [math]C_{m,n,l}[/math].
- Для всех [math]i=0..M_x, j=0..M_y, k=0..M_z[/math] вычислить [math]\hat{u}_{h,i,j,k}[/math].
1.5 Схема реализации последовательного алгоритма
Первый этап на языке Fortran (для наглядности вложенные конструкции упрощены):
Do i j k = 1 1 1, Nx Ny Nz
r = 0.0D0
Do i0 j0 k0 = 1 1 1, Mx My Mz
x = i0*dx
y = j0*dy
z = k0*dz
r = r + dx*dy*dz*f(i0,j0,k0)*Sin(Pi*i*x/Lx)*Sin(Pi*j*y/Ly)*Sin(Pi*k*z/Lz)
End Do
c(i, j, k) = 8*r / (Pi**2*(Ly*Lz/Lx*i**2 + Lx*Lz/Ly*j**2 + Lx*Ly/Lz*k**2))
End Do
Второй этап:
Do i0 j0 k0 = 0 0 0, M_x M_y M_z
x = i0*dx
y = j0*dy
z = k0*dz
s = 0.0D0
Do i j k = 1 1 1, N_x N_y N_z
s = s + c(i, j, k)*Sin(Pi*i*x/Lx)*Sin(Pi*j*y/Ly)*Sin(Pi*k*z/Lz)
End Do
u(i0, j0, k0) = s
End Do
1.6 Последовательная сложность алгоритма
Вычислительную сложность первого варианта алгоритма можно оценить как [math]O(N_x N_y N_z M_x M_y M_z)[/math] операций с плавающей точкой.
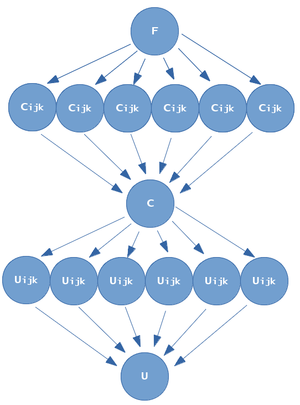
1.7 Информационный граф
- На нулевом ярусе алгоритма происходит генерация или считывание правой части уравнения.
- На первом ярусе вычисляются коэффициенты.
- На втором ярусе происходит объединение их в общий массив.
- На третьем ярусе вычисляется сеточная функция.
- На четвертом ярусе происходит вывод.
1.8 Ресурс параллелизма алгоритма
Из информационного графа видно, что можно коэффициенты [math]C_{m,n,l}[/math] и [math]\hat{u}_{h,i,j,k}[/math] можно вычислять параллельно. Так как каждое из этих значение вычисляется в виде сумм, дополнительный параллелизм можно достичь за счет параллельного суммирования. Таким образом, при количестве [math]P[/math] вычислительных узлов, при [math]P \le min(N_x N_y N_z, M_x M_y M_z)[/math] можно достичь производительности в [math]O(\frac{N_x N_y N_z M_x M_y M_z}{P})[/math] операций.
При [math]P \gt min(N_x N_y N_z, M_x M_y M_z)[/math], положив [math]Q = mod(P, min(N_x N_y N_z, M_x M_y M_z))[/math], за счет параллельного суммирования, эта величина равна [math]O(\frac{N_x N_y N_z + M_x M_y M_z}{Q})[/math].
1.9 Входные и выходные данные алгоритма
В качестве входных данных выступает трехмерный массив [math]M_x \times M_y \times M_z[/math] правой части уравнения. Выходной массив - трехмерный массив решения той же размерности.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Для оценки масштабируемости были выбраны значения [math]N_x=N_y=N_z=M_x=M_y=M_z=64[/math]. Все тесты проводились на суперкомпьютере Ломоносов-1.
Анализируя график, видно, что производительность растет линейно с увеличением количества вычислительных узлов. Шкала на данном графике логарифмическая. Это можно объяснить отсутствием расходом на обмен данными между процессами при вычислении коэффициентов приближенного решения и значений функции.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
Абакумов М.В., Гулин А.В. Лекции по численным методам математической физики: Учеб. пособие. - М.:ИНФРА-М,2013
Самарский А. А. Введение в численные методы, 1982.