Участник:Grachovamc/Интегрирование методом Монте - Карло: различия между версиями

Версия 21:25, 29 ноября 2017

Содержание

1 Свойства и структура алгоритма
2 Программная реализация алгоритма
3 Литература

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Монте-Карло — общее название группы численных методов, основанных на получении большого числа реализаций стохастического процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Метод Монте-Карло имеет множество различных приложений. Он применяется для решения задач в различных областях математики, физики, химии, биологии, экономики, оптимизации, теории управления и др.

Годом рождения метода Монте-Карло считается 1949 год, когда в свет выходит статья Метрополиса и Улама «Метод Монте-Карло»^[1]. Название метода происходит от названия города в княжестве Монако, широко известного своими многочисленными казино, поскольку именно рулетка является одним из самых широко известных генераторов случайных чисел.

Особенностью данного метода является простая структура вычислительного алгоритма. Как правило, составляется программа для осуществления одного случайного испытания, затем это испытание повторяется N раз, причем каждый опыт не зависит от остальных. Для получения итогового значения усредняются результаты всех опытов. Поэтому метод Монте - Карло также иногда называют методом статистических испытаний^[2].

Большим преимуществом метода Монте-Карло является то, что он позволяет учесть в модели элемент случайности и сложность реального мира. Кроме того, метод является робастным по отношению к изменению различных параметров, таких как распределение случайной величины.

Рассмотрим использование метода Монте — Карло для задачи вычисления интегралов.

Предположим, требуется взять определенный интеграл от некоторой функции. Его значение будет численно равно площади под графиком данной функции.

Для определения этой площади можно разбить отрезок, по которому производится интегрирование, на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. И если предположить, что в случае функции одной переменной достаточно разбиения на 50 подотрезков и, соответственно, 50 вычислений значений функции, то в случае функции [math]n[/math] переменных количество подотрезков и вычислений значений функции возрастает до [math]50^n[/math]. При размерности функции больше 10 задача становится очень громоздкой. Поскольку пространства большой размерности встречаются во многих задачах, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло.

1.2 Математическое описание алгоритма

1.2.1 Интегрирование функции одной переменной

Рассмотрим два наиболее распространенных варианта использования метода Монте - Карло для вычисления интегралов.

1.2.1.1 Метод усреднения подынтегральной функции

Рассмотрим интеграл вида

[math]I = \int_a^b \phi(x) dx[/math]

Пусть [math]X[/math] - случайная величина, равномерно распределенная на отрезке интегрирования [math][a, b][/math] с плотностью [math]f(x) = \frac{1}{b - a}[/math].

Тогда [math]\phi(X)[/math] также является случайной величиной, и ее математическое ожидание выражается как

[math]\mathbb{E}\phi(X)=\int\limits_a^b \phi(x)f(x) dx = \frac{1}{b - a}\int\limits_a^b \phi(x) dx[/math]

Отсюда

[math]\int_a^b \phi(x) dx = (b - a)\mathbb{E}\phi(X)[/math]

Заменив математическое ожидание [math]\mathbb{E}\phi(X)[/math] его оценкой – выборочным средним, получим оценку интеграла

[math]\int\limits_{a}^{b}\phi(x)\,dx\approx\frac{b-a}{N}\sum^{N}_{i=1}\phi(x_i)[/math],

где [math]x_i[/math] – возможные значения случайной величины [math]X[/math], [math]N[/math] – число испытаний.

1.2.1.2 Геометрический метод

Рассмотрим интеграл вида

[math]I = \int_a^b \phi(x) dx[/math], где подынтегральная функция неотрицательна и ограничена [math]0 \le \phi(x) \le c[/math] для любого [math]x \in [a, b][/math].

Согласно геометрическому определению интеграла для вычисления значения интеграла определим площадь под графиком интегрируемой функции.

Для этого применяется следующий стохастический алгоритм:

функция ограничивается прямоугольником площадью [math]S[/math];
в данном прямоугольнике случайным образом выбираются координаты [math]N[/math] точек;
определяется число точек [math]n[/math], координаты которых попали под график функции; тогда выполняется соотношение [math]\frac{\int\limits_a^b \phi(x) dx}{S} \approx \frac{n}{N}[/math]
искомая оценка интеграла равна [math]S\frac{n}{N}[/math].

1.2.2 Вычисление кратного интеграла

Случай вычисления [math]n[/math] - мерного интеграла аналогичен одномерному случаю с учетом некоторых корректировок.

1.2.2.1 Метод усреднения подынтегральной функции

Пусть функция [math]y = f(x_1, x_2,...,x_n)[/math] непрерывна в ограниченной замкнутой области [math]D[/math], и требуется вычислить [math]n[/math]-кратный интеграл [math]I[/math] по области [math]D[/math]:

[math]I = {\int\limits_{D}{\ldots \int{f\left( {{x}_{1}},\ldots ,{{x}_{n}} \right)d{{x}_{1}}\ldots d{{x}_{n}}}}}[/math]

Геометрически число [math]I[/math] представляет собой [math](m + 1)[/math] - мерный объем вертикального цилиндрического тела в пространстве [math]Ox_1x_2...x_ny[/math], построенного на основании [math]D[/math] и ограниченного сверху соответствующим куском поверхности [math]y = f(\vec x)[/math],где [math]\vec x = (x_1, ..., x_n)[/math].

Пусть область интегрирования [math]D[/math] расположена в [math]n[/math]-мерном параллелепипеде [math]a_k \le x_k \le b_k[/math], [math]k = 1,...,n[/math]. Преобразуем интеграл таким образом, чтобы новая область интегрирования целиком находилась внутри единичного [math]n[/math] - мерного куба. Для этого сделаем замену переменных [math]x_k = a_k + (b_k - a_k) y_k[/math], [math]k = 1,...,n[/math]. Тогда [math]0 \le y_k \le 1[/math], [math]k = 1,...,n[/math]. Следовательно новая область интегрирования [math]G[/math] целиком расположена в единичном [math]n[/math]-мерном кубе.

Таким образом, получаем выражение [math]I = \frac{D(x_1,...x_n)}{D(y_1,...y_n)}I'[/math], где якобиан преобразования имеет вид

[math]\frac{D(x_1,...x_n)}{D(y_1,...y_n)} = (b_1 - a_1)...(b_n - a_n)[/math],

[math]I' = {\int\limits_{G}{\ldots \int{g\left( {{y}_{1}},\ldots ,{{y}_{n}} \right)d{{y}_{1}}\ldots d{{y}_{n}}}}} = {\int\limits_{G}{\ldots \int{f\left( {a_1 + (b_1 - a_1)y_1},\ldots ,{a_n + (b_n - a_n)y_n} \right)d{{y}_{1}}\ldots d{{y}_{n}}}}}[/math],

а область интегрирования [math]G[/math] расположена внутри [math]n[/math] - мерного единичного куба [math]0 \le y_k \le 1[/math], [math]k = 1,...,n[/math].

Выберем [math]N[/math] равномерно распределенных на отрезке [math][0, 1][/math] последовательностей случайных величин [math]\vec y^{(i)} = ({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})[/math], [math]i = 1,...,N[/math]. Эти последовательности являются координатами случайных точек [math]K_i({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})[/math].

Далее определим, какие из этих точек принадлежат области интегрирования [math]G[/math].

Пусть таких точек всего [math]m[/math]. Тогда при достаточно большом [math]m[/math] можно считать, что [math]g_{mean} = \mathbb{E}g(K) \approx \tilde{g}_{mean} = \frac{1}{m}\sum^{m}_{i=1}g(K_i) [/math]. Следовательно оценка интеграла [math]I'[/math] имеет вид [math]I' = \tilde{g} * V_G[/math], где [math]V_G[/math] - [math]n[/math] - мерный объем области интегрирования [math]G[/math].

Из определения геометрической вероятности примем [math]V_G \approx \tilde{V}_G = \frac{m}{N}[/math].

Таким образом, оценка искомого интеграла имеет вид [math]I = V_{par} * \tilde{g}_{mean} * \tilde{V}_G = \frac{V_{par}}{N}\sum^{m}_{i=1}g(K_i)[/math], где [math]V_{par} = (b_1 - a_1)...(b_n - a_n)[/math] - объем параллепипеда, ограничивающего исходную область интегрирования [math]D[/math].

1.2.2.2 Геометрический метод

В случае использования геометрического метода осуществляется та же последовательность действий, что и при использовании данного метода в случае функции одной переменной с учетом того, что функция ограничивается [math]n[/math] - мерным параллелепипедом, и, соответственно, в результирующей формуле вместо площади прямоугольника берется объем ограничивающего функцию параллелепипеда.

1.3 Вычислительное ядро алгоритма

Таким образом, вычислительным ядром последовательной реализации любого из представленных вариантов метода Монте - Карло интегрирования является многократное вычисление значения функции в случайной точке.

1.4 Макроструктура алгоритма

Согласно описанию вычислительного ядра алгоритма в качестве макровершины можно взять вычисление подынтегральной функции в случайной точке.

1.5 Схема реализации последовательного алгоритма

1.5.1 Интегрирование функции одной переменной

1.5.1.1 Метод усреднения подынтегральной функции

Последовательность исполнения метода следующая:

1. Генерация последовательности [math]{{\{x_i\}}_{i = 1}}^{N}[/math] значений случайной величины, равномерно распределенной на отрезке интегрирования [math][a, b][/math]. Для экономии памяти лучше генерировать не всю случайную последовательность целиком, а по одному значению в цикле.

2. Вычисление значений функции [math]\phi(x_i)[/math] в каждой из точек последовательности [math]{{\{x_i\}}_{i = 1}}^{N}[/math].

3. Вычисление выборочного среднего [math]\frac{1}{N}\sum^{N}_{i=1}\phi(x_i)[/math].

4. Получение искомого значения интеграла согласно формуле [math]\int\limits_{a}^{b}\phi(x)\,dx\approx\frac{b-a}{N}\sum^{N}_{i=1}\phi(x_i)[/math].

1.5.1.2 Геометрический метод

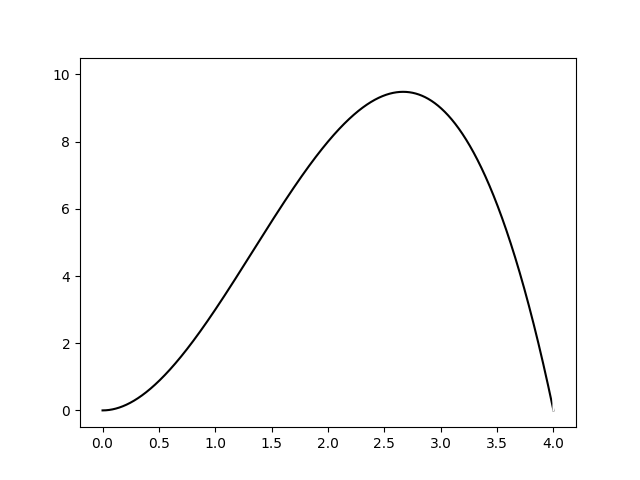
Пусть интегрируемая функция имеет следующий вид

Последовательность исполнения метода следующая:

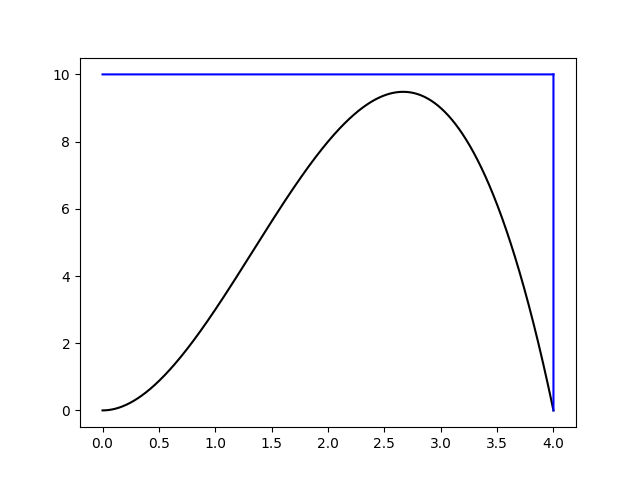
1. Функция ограничивается прямоугольником площадью [math]S[/math]

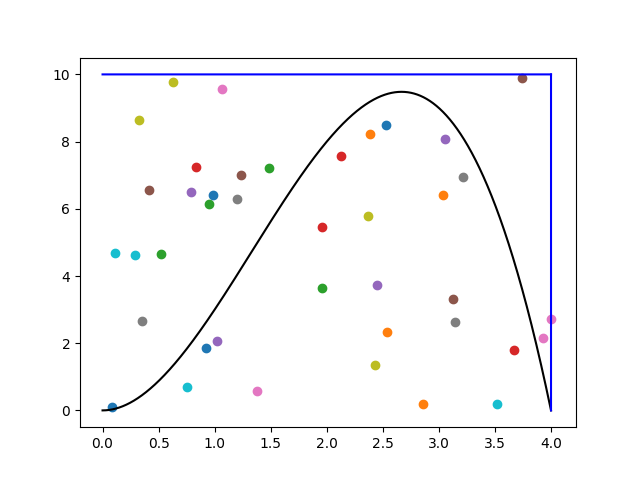
2. В прямоугольнике случайным образом выбираются координаты [math]N[/math] точек

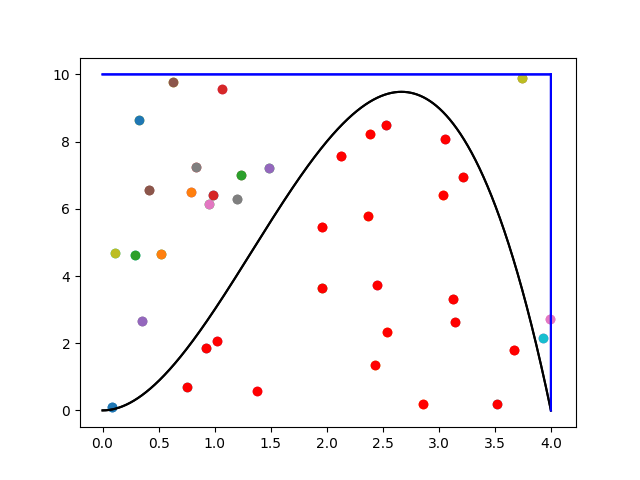
3. Определяется число [math]n[/math] точек, координаты которых попали под график функции

4. Искомая площадь вычисляется согласно формуле [math]S\frac{n}{N}[/math]

1.5.2 Вычисление кратного интеграла

1.5.2.1 Метод усреднения подынтегральной функции

Последовательность выполнения метода следующая:

1. Преобразование интеграла таким образом, чтобы новая область интегрирования [math]G[/math] целиком находилась внутри единичного [math]n[/math] - мерного куба с использованием замены переменных [math]x_k = a_k + (b_k - a_k) y_k[/math], [math]k = 1,...,n[/math].

2. Вычисление якобиана преобразования и получение следующего выражения получаем выражение [math]I = \frac{D(x_1,...x_n)}{D(y_1,...y_n)}I'[/math], где якобиан преобразования имеет вид

[math]\frac{D(x_1,...x_n)}{D(y_1,...y_n)} = (b_1 - a_1)...(b_n - a_n)[/math], [math]I' = {\int\limits_{G}{\ldots \int{g\left( {{y}_{1}},\ldots ,{{y}_{n}} \right)d{{y}_{1}}\ldots d{{y}_{n}}}}} = {\int\limits_{G}{\ldots \int{f\left( {a_1 + (b_1 - a_1)y_1},\ldots ,{a_n + (b_n - a_n)y_n} \right)d{{y}_{1}}\ldots d{{y}_{n}}}}}[/math].

3.Выбор [math]N[/math] равномерно распределенных на отрезке [math][0, 1][/math] последовательностей случайных величин [math]\vec y^{(i)} = ({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})[/math], [math]i = 1,...,N[/math], которые являются координатами случайных точек [math]K_i({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})[/math].

4. Определение того, какие из этих точек принадлежат области интегрирования [math]G[/math]. Пусть таких точек всего [math]m[/math].

5. Вычисление [math]g_{mean} = \mathbb{E}g(K) \approx \tilde{g}_{mean} = \frac{1}{m}\sum^{m}_{i=1}g(K_i) [/math].

6. Получение оценки интеграла [math]I' = \tilde{g}_{mean} * V_G[/math], где [math]V_G[/math] - [math]n[/math] - мерный объем области интегрирования [math]G[/math]. Считаем, что [math]V_G \approx \tilde{V}_G = \frac{m}{N}[/math].

7. Получение оценки искомого интеграла [math]I = V_{par} * \tilde{g}_{mean} * \tilde{V}_G = \frac{V_{par}}{N}\sum^{m}_{i=1}g(K_i)[/math], где [math]V_{par} = (b_1 - a_1)...(b_n - a_n)[/math] - объем параллелепипеда, ограничивающего исходную область интегрирования [math]D[/math].

1.5.3 Геометрический метод

Схема реализации последовательного алгоритма аналогична одномерному случаю.

1.6 Последовательная сложность алгоритма

Для вычисления определенного интеграла методом Монте - Карло требуется осуществить:

1) при использовании метода усреднения подынтегральной функции

N генераций случайных величин;
N вычислений значений функции;
N - 1 сложение.

2) при использовании геометрического метода

N генераций случайных величин;
N вычислений значений функции;
N сравнений.

Таким образом, алгоритм является линейным относительно количества случайных точек.

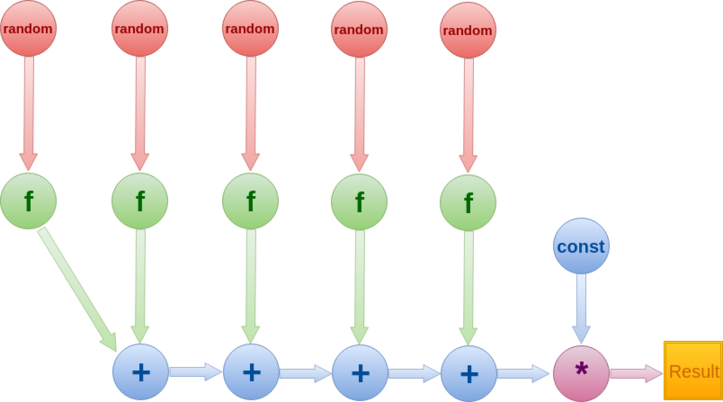
1.7 Информационный граф

Рисунок 1. Граф алгоритма при использовании метода усреднения подынтегральной функции

Рисунок 2. Граф алгоритма при использовании геометрического метода

1.8 Ресурс параллелизма алгоритма

Для вычисления интеграла методом Монте - Карло при использовании усреднения подынтегральной функции требуется последовательно выполнить следующие ярусы:

1 ярус генераций случайных величин (N * p генераций, где N - изначально выбранное количество точек, p - кратность интеграла);
1 ярус вычислений значений функции в полученных ранее случайных точках (N вычислений);
1 ярус сложений (N - 1 сложение);
1 ярус умножений (1 умножение на константу).

Для вычисления интеграла методом Монте - Карло при использовании геометрической интерпретации требуется последовательно выполнить следующие ярусы:

1 ярус генераций случайных величин (N * p генераций, где N - изначально выбранное количество точек, p - кратность интеграла);
1 ярус вычислений значений функции в полученных ранее случайных точках (N вычислений);
1 ярус сравнений (N сравнений);
1 ярус сложений (N - 1 сложений);
1 ярус умножений (1 умножение на константу).

Таким образом, алгоритм отлично поддается распараллеливанию, так как все вычисления функции f могут производиться независимо в общем случае.

При классификации по высоте ярусно-параллельной формы алгоритм метода Монте - Карло имеет сложность 4 или 5 в зависимости от конкретного выбора одного из двух предлагаемых вариантов. При классификации по ширине его сложность будет [math]O(N)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: подынтегральная функция [math]f[/math], кратность интеграла [math]p[/math], пределы интегрирования и количество генерируемых случайных точек [math]N[/math].

Выходные данные: число - искомое значение интеграла.

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным (отношение линейной сложности к константной).

При ограниченных ресурсах последовательная и параллельная реализации имеют линейную сложность относительно количества точек интегрирования. В данном случае соотношение последовательной и параллельной сложности равно константе, которая может быть достаточно значительной и приближаться к количеству доступных узлов.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна.

Алгоритм интегрирования методом Монте - Карло не является детерминированным, так он главным образом основывается на генерации случайных величин, в связи с чем невозможно получить точный и предопределенный заранее результат. Поэтому для достижения необходимой точности выбирается допустимая погрешность.

Выведем формулу для вычисления значения погрешности:

[math]\Delta I = \Delta(V_{par} * \tilde{g}_{mean} * \tilde{V_G}) = V_{par} * (\Delta g_{mean} * \tilde{V_G} + \Delta V_G * |\tilde{g}_{mean}|)[/math].

По центральной предельной теореме

[math] P \left\{ |g_{mean} - \tilde{g}_{mean}| \le t_{\beta}\sqrt{\frac{\sigma_{1}^2}{m}} \right\} \approx \beta [/math], [math] P \left\{ |V_G - \tilde{V}_G| \le t_{\beta}\sqrt{\frac{\sigma_{2}^2}{N}} \right\} \approx 2\Phi(t_{\beta}) = \beta [/math],

где [math]\beta[/math] - коэффициент доверия, [math]\Phi(t)[/math] - функция стандартного нормального распределения, [math]\sigma_{1}^2 = D[g(K)], \sigma_{2}^2 = D[V_G][/math].

То есть с вероятностью [math]\beta[/math]

[math]\Delta g_{mean} = t_{\beta} \sqrt{\frac{\sigma_{1}^2}{m}}, \Delta V_G = t_{\beta} \sqrt{\frac{\sigma_{2}^2}{N}}[/math].

При этом [math]\tilde{g}_{mean} = \frac{1}{m}\sum^{m}_{i=1}g(K_i), \tilde{V}_{G} = \frac{m}{N} [/math].

Таким образом,

[math]\Delta I = V_{par} * t_{\beta} (\sigma_1 * \frac{\tilde{V}_G}{m} + \sigma_2 * \frac{|\tilde{g}_{mean}|}{N})[/math].

Обычно величины [math]\sigma_1^2[/math] и [math]\sigma_2^2[/math] оказываются неизвестными, тогда их приближенные значения вычисляются по формулам

[math]\tilde{\sigma}_1^2 \approx (\tilde{g}^2)_{mean} - (|\tilde{g}_{mean}|)^2[/math], где [math](\tilde{g}^2)_{mean} = \frac{1}{m}\sum^{m}_{i=1}g^2(K_i)[/math];

[math]\tilde{\sigma}_2^2 \approx \tilde{V}_G (1 - \tilde{V}_G)[/math].

Таким образом, получаем следующее соотношение для погрешности интегрирования методом Монте - Карло:

[math]\Delta I = V_{par} * t_{\beta} (\tilde{\sigma}_1 * \frac{\sqrt{\tilde{V}_G}}{\sqrt{N}} + \tilde{\sigma}_2 * \frac{|\tilde{g}_{mean}|}{\sqrt{N}})[/math].

Если полученное значение погрешности велико, то можно назначить желаемую погрешность, на ее основании вычислить необходимое количество испытаний и затем определить значение интеграла с требуемым количеством испытаний.

Дуги информационного графа являются полностью локальными.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.1.1 Метод усреднения подынтегральной функции

Код последовательной реализации для случая использования метода усреднения подынтегральной функции на языке C может выглядеть так:

double integral(long int N, int order, double *limits, double *add_limits, double v_par)
{
    double coord[order], res;
    int n, i, ind;
    res = 0.0;
    for (n = 1; n <= N; n++) {
        ind = 0;
        for (i = 0; i < order; i++) {
            coord[i] = (double)(rand())/RAND_MAX;
            if (coord[i] > limits[2 * i + 1] || coord[i] < limits[2 * i]) {
                ind = 1;
                break;
            }
        }
        if (ind == 0)
            res = res + f(coord, order, add_limits);
    }
    return(res / (double)N * v_par);
}

2.1.2 Геометрический метод

Код последовательной реализации для случая использования геометрического метода на языке C может выглядеть так:

double integral(long int N, int order, double *limits, double *add_limits, double v_par)
{
    double coord[order];
    int n, i, ind, score;
    res = 0.0;
    for (n = 1; n <= N; n++) {
        ind = 0;
        for (i = 0; i < order; i++) {
            coord[i] = (double)(rand())/RAND_MAX;
            if (coord[i] > limits[2 * i + 1] || coord[i] < limits[2 * i]) {
                ind = 1;
                break;
            }
        }
        if (ind == 0)
            score++;
    }
    return(score / (double)N * v_par);
}

2.2 Локальность данных и вычислений

Локальность вычислений существенно определяется реализацией вычисления функции f. В предположении, что данная реализация уже имеется, будем считать, что в ней учтены требования эффективного использования памяти.

2.3 Возможные способы и особенности параллельной реализации алгоритма

Самым очевидным вариантом реализации параллельного алгоритма является независимое вычислении функции f в генерируемых случайных точках различными вычислительными узлами. Это может быть реализовано как при помощи технологии threads или OpenMP при запуске на одном узле, так и при использовании межпроцессорных обменов при помощи MPI. Головной узел передает остальным вычислительным узлам реализацию функции f и точки или наборы точек, в которых должна вычисляться функция.

Однако при такой реализации нужно уделять особое внимание генерации случайных чисел, которая должна быть независимой на каждом вычислительном узле. Поскольку при вычислениях методом Монте-Карло существенное количество операций расходуется для оперирования над случайными числами, то наличие простых и экономных способов формирования последовательности случайных чисел во многом определяет возможность практического использования этого метода. Обычно для подобных задач используется генерация равномерно распределенных на интервале (0, 1) случайных величин, так как такой способ требует мало машинного времени и обеспечивает простоту дальнейших преобразований. Но в связи с тем, что в языках программирования используются генераторы псевдослучайных чисел, важно, чтобы они имели достаточно длинный период, гарантирующий отсутствие зацикливания последовательности в пределах решаемой задачи.

Для более эффективной и быстрой работы алгоритма возможно использование более сложных реализаций, которые будут требовать уточнения класса подынтегральных функций и следовательно соответствующей модификации алгоритма их вычисления.

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

↑ N. Metropolis, S. Ulam The Monte Carlo Method, — J. Amer. statistical assoc. 1949 44 № 247 335—341.
↑ Соболь И. М. Метод Монте-Карло. — М.: Наука, 1968. — 64 с. — (Популярные лекции по математике). — 79 000 экз.

[1] N. Metropolis, S. Ulam The Monte Carlo Method, — J. Amer. statistical assoc. 1949 44 № 247 335—341.

[2] Соболь И. М. Метод Монте-Карло. — М.: Наука, 1968. — 64 с. — (Популярные лекции по математике). — 79 000 экз.

[1]

[2]

@@ Строка 132: / Строка 132: @@
 Последовательность выполнения метода следующая:
-. Преобразование интеграла таким образом, чтобы новая область интегрирования G целиком находилась внутри единичного <math>n</math> - мерного куба с использованием замены переменных <math>x_k = a_k + (b_k - a_k) y_k</math>, <math>k = 1,...,n</math>.
+. Преобразование интеграла таким образом, чтобы новая область интегрирования <math>G</math> целиком находилась внутри единичного <math>n</math> - мерного куба с использованием замены переменных <math>x_k = a_k + (b_k - a_k) y_k</math>, <math>k = 1,...,n</math>.
 . Вычисление якобиана преобразования и получение следующего выражения получаем выражение <math>I = \frac{D(x_1,...x_n)}{D(y_1,...y_n)}I'</math>, где якобиан преобразования имеет вид
@@ Строка 138: / Строка 138: @@
 <math>\frac{D(x_1,...x_n)}{D(y_1,...y_n)} = (b_1 - a_1)...(b_n - a_n)</math>, <math>I' = {\int\limits_{G}{\ldots \int{g\left( {{y}_{1}},\ldots ,{{y}_{n}} \right)d{{y}_{1}}\ldots d{{y}_{n}}}}} = {\int\limits_{G}{\ldots \int{f\left( {a_1 + (b_1 - a_1)y_1},\ldots ,{a_n + (b_n - a_n)y_n} \right)d{{y}_{1}}\ldots d{{y}_{n}}}}}</math>.
-.Выбор N равномерно распределенных на отрезке <math>[0, 1]</math> последовательностей случайных величин <math>\vec y^{(i)} = ({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})</math>, <math>i = 1,...,N</math>, которые являются координатами случайных точек <math>K_i({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})</math>.
+.Выбор <math>N</math> равномерно распределенных на отрезке <math>[0, 1]</math> последовательностей случайных величин <math>\vec y^{(i)} = ({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})</math>, <math>i = 1,...,N</math>, которые являются координатами случайных точек <math>K_i({y^{(i)}}_{1}, ..., {y^{(i)}}_{n})</math>.
-. Определение того, какие из этих точек принадлежат области интегрирования G. Пусть таких точек всего m.
+. Определение того, какие из этих точек принадлежат области интегрирования <math>G</math>. Пусть таких точек всего <math>m</math>.
-. Вычисление <math>\mathbb{E} g(K) = \frac{1}{m}\sum^{m}_{i=1}g(K_i) </math>.
+. Вычисление <math>g_{mean} = \mathbb{E}g(K) \approx \tilde{g}_{mean} = \frac{1}{m}\sum^{m}_{i=1}g(K_i) </math>.
-. Получение оценки интеграла <math>I'</math>: <math>I' = \mathbb{E} g(K) * V_G</math>, где <math>V_G</math> - <math>n</math> - мерный объем области интегрирования G. Считаем, что <math>V_G = V_{G mean} = \frac{m}{N}</math>.
+. Получение оценки интеграла <math>I' = \tilde{g}_{mean} * V_G</math>, где <math>V_G</math> - <math>n</math> - мерный объем области интегрирования <math>G</math>. Считаем, что <math>V_G \approx \tilde{V}_G = \frac{m}{N}</math>.
+. Получение оценки искомого интеграла <math>I = V_{par} * \tilde{g}_{mean} * \tilde{V}_G = \frac{V_{par}}{N}\sum^{m}_{i=1}g(K_i)</math>, где <math>V_{par} = (b_1 - a_1)...(b_n - a_n)</math> - объем параллелепипеда, ограничивающего исходную область интегрирования <math>D</math>.
-. Получение оценки искомого интеграла <math>I = V_{par} * \mathbb{E} g(K) * V_{G mean} = \frac{V_{par}}{N}\sum^{m}_{i=1}g(K_i)</math>, где <math>V_{par} = (b_1 - a_1)...(b_n - a_n)</math> - объем параллепипеда, ограничивающего исходную область интегрирования D.
 ==== Геометрический метод ====
 Схема реализации последовательного алгоритма аналогична одномерному случаю.