Участник:Sveta: различия между версиями
Sveta (обсуждение | вклад) |
Sveta (обсуждение | вклад) |
||
| (не показаны 42 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | Основные авторы описания: [[Участник:Sveta|Закирова С.В.]] | |
| − | + | Поиск равновесия в дуополии Штакельберга | |
== Свойства и структура алгоритмов == | == Свойства и структура алгоритмов == | ||
| Строка 8: | Строка 8: | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| − | Есть множество стратегий первого игрока <math> X </math> и | + | Есть множество стратегий первого игрока <math> X </math> и множество стратегий <math> Y </math> второго игрока. |
| − | Первым ходит игрок, называемый лидером, его стратегия <math> x \in X </math>. Второй игрок, называемый подчиненным, ходит стратегией <math> y \in Y </math>. У каждого игрока есть своя функция выигрыша. Для лидера это функция <math> H(x,y) </math>. | + | Первым ходит игрок, называемый лидером, его стратегия <math> x \in X </math>. Второй игрок, называемый подчиненным, ходит стратегией <math> y \in Y </math>. У каждого игрока есть своя функция выигрыша. Для лидера это функция <math> H(x,y) </math>. |
| − | Для подчиненного <math> G(x,y) </math>. Оба хотят максимизировать свой выигрыш, при условии лояльности(лояльность, это когда при условии одинакового выигрыша для второго, он максимизирует выигрыш первого) второго игрока по отношении к первому. Набор стратегий <math> (x^*,y^*) </math> называется равновесием Штакельберга, если <math> y^* = R(x^*) </math> есть наилучший ответ подчиненного на стратегию лидера, которая находится как решение задачи <math> H(x^*, y^*) = max H(x,R(x)) </math> | + | Для подчиненного <math> G(x,y) </math>. Оба хотят максимизировать свой выигрыш, при условии лояльности(лояльность, это когда при условии одинакового выигрыша для второго, он максимизирует выигрыш первого) второго игрока по отношении к первому. Набор стратегий <math> (x^*,y^*) </math> называется равновесием Штакельберга<ref> Васин А.А., Морозов В.В. "Введение в теорию игр с приложениями в экономике"(учебное пособие). - М.: 2003. - 278 с. Pages 131-132 </ref>, если <math> y^* = R(x^*) </math> есть наилучший ответ подчиненного на стратегию лидера, которая находится как решение задачи <math> H(x^*, y^*) = max H(x,R(x)) </math> (максимум берется по всем стратегиям <math>x</math> из <math>X</math>) |
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | + | Вычислительным ядром данного алгоритма является поиск максимума в строке. Таким образом мы находим наилучший ответ второго игрока. | |
| − | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | + | Как уже сказано в пункте выше, основнуая составляющая часть алгоритма это поиск максимума в строке. | |
| + | Алгоритм можно представить как многократное повторение(по количеству строк) поиска максимума в строках первой матрицы. После этого поиск максимума по элементам второй матрицы, индексы которых уже были найдены в первой итерации. | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| Строка 32: | Строка 32: | ||
int main(int argc, char *argv[]) | int main(int argc, char *argv[]) | ||
{ | { | ||
| + | //считиываем m и n | ||
int n = strtol(argv[1], NULL, 10); | int n = strtol(argv[1], NULL, 10); | ||
int m = strtol(argv[2], NULL, 10); | int m = strtol(argv[2], NULL, 10); | ||
| + | //создаем матрицы G и H | ||
vector<vector<double>> H(n, vector<double>(m)); | vector<vector<double>> H(n, vector<double>(m)); | ||
vector<vector<double>> G(n, vector<double>(m)); | vector<vector<double>> G(n, vector<double>(m)); | ||
| + | //инициализируем матрицы G и H | ||
srand(time(NULL)); | srand(time(NULL)); | ||
for(int i = 0; i < n; ++i) { | for(int i = 0; i < n; ++i) { | ||
| Строка 46: | Строка 49: | ||
} | } | ||
| + | //ищем максимум в G благожелательно к лидеру на каждую его стратегию | ||
vector<int> ind(n); | vector<int> ind(n); | ||
for(int i = 0; i < n; ++i){ | for(int i = 0; i < n; ++i){ | ||
| Строка 64: | Строка 68: | ||
} | } | ||
| + | //ищем с учетом ответа второго наилучшую тратегию для лидера | ||
int str_h = 0; | int str_h = 0; | ||
for(int i = 0; i < n; ++i) { | for(int i = 0; i < n; ++i) { | ||
| Строка 73: | Строка 78: | ||
} | } | ||
| + | |||
</source> | </source> | ||
| − | |||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 81: | Строка 86: | ||
Для второй части - поиска наилучших стратегий первого потребуется <math> n </math> операций сравнения. | Для второй части - поиска наилучших стратегий первого потребуется <math> n </math> операций сравнения. | ||
| − | Таким образом результирующая сложность алгоритма - <math> n * m </math> операций. | + | Таким образом результирующая сложность алгоритма - <math> О(n * m) </math> операций. |
=== Информационный граф === | === Информационный граф === | ||
Опишем граф алгоритма в виде рисунка. | Опишем граф алгоритма в виде рисунка. | ||
| − | [[ | + | [[File:Информационный граф РШ.png]] |
| + | |||
| + | Круглые элеменеты графа - элементы матрицы G. Под max, имеется в виду функция поиска максимума в строке (причем с уметом благожелательности). | ||
| + | max2 - опять же функция поиска максимума для первого, исходя из ответов второго. | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | Каждую строку можно обрабатывать отдельным процессором. Таким образом каждый процессор бежит по строке и ищет там максимум (с условием благосклонности к лидеру). После этого процессоры синхронизируются и мы ищем максимум из уже найденых значений, таким образом мы получаем наибольший выигрыш для лидера, после чего находим все равновесия по Штакельбергу. | ||
| + | Параллельная сложность: <math>О(m)</math>, где <math>m</math> число столбцов а нашей матрице. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
Входными данными являются пара матриц <math> H(x,y) </math>, <math> G(x,y) </math> одинакового размера <math>n * m </math> (стратегии обоих игроков). Выходные данные это множество пар чисел <math> (x^*,y^*) </math>, где каждая из пар является равновесием по Штакельбергу в нашей дуаполии. | Входными данными являются пара матриц <math> H(x,y) </math>, <math> G(x,y) </math> одинакового размера <math>n * m </math> (стратегии обоих игроков). Выходные данные это множество пар чисел <math> (x^*,y^*) </math>, где каждая из пар является равновесием по Штакельбергу в нашей дуаполии. | ||
| + | == Программная реализация алгоритма == | ||
| + | |||
| + | === Особенности реализации последовательного алгоритма === | ||
| − | == | + | === Локальность данных и вычислений === |
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
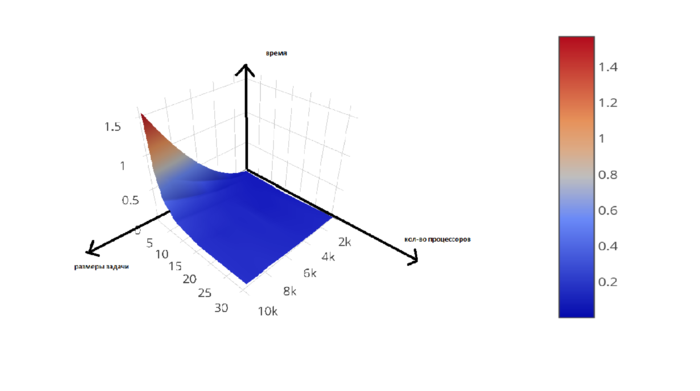
| + | Проведём исследование масштабируемости параллельной реализации алгоритма. Набор и границы значений изменяемых параметров запуска реализации алгоритма: | ||
| + | |||
| + | число процессоров [1,2 4, 8 : 32] со значениями квадрата целого числа; | ||
| + | |||
| + | размер матрицы(для тестов бралась квадратная матрица) [1000:10000] с шагом 1000. | ||
| + | |||
| + | На следующем рисунке приведен график производительности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска. | ||
| + | [[Файл:График_РШ.png |thumb|center|700px|Рис.1. График маштабируемости]] | ||
| + | |||
| + | '''сведения о программно-аппаратной среде''' | ||
| + | |||
| + | компьютер: суперкомпьютор Ломоносов | ||
| + | |||
| + | компилятор с использованными опциями оптимизации: mpicxx версии openmpi/1.8.4-gcc | ||
| + | |||
| + | библиотеки: #include <mpi.h>, #include <iostream>, #include <cstdlib>, #include <ctime>, #include <vector> | ||
| + | |||
| + | '''выводы о масштабируемости''' | ||
| + | |||
| + | Мы получили ожидаемые результаты(в целом), что производительность увеличивается с | ||
| + | увеличеснием количества процессоров и уменьшается с увеличеннием количества строк. | ||
| + | Это можно объяснить тем, что выбранный алгоритм очень хорошо распараллеливается, а | ||
| + | «общение» процессоров почти не требуется (это важно так как эта процедура достаточно | ||
| + | ресурсозатратна). | ||
| + | |||
| + | === Динамические характеристики и эффективность реализации алгоритма === | ||
| + | |||
| + | === Выводы для классов архитектур === | ||
| + | |||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | Написанная мной, текущая реализация алгоритма: | ||
| + | <source lang="C++"> | ||
| + | |||
| + | #include <mpi.h> | ||
| + | #include <iostream> | ||
| + | #include <cstdlib> | ||
| + | #include <ctime> | ||
| + | #include <vector> | ||
| + | |||
| + | using namespace std; | ||
| + | |||
| + | |||
| + | int main(int argc, char * argv[]) | ||
| + | { | ||
| + | |||
| + | int comm_sz, my_rank; | ||
| + | MPI_Init(&argc, &argv); | ||
| + | MPI_Comm comm = MPI_COMM_WORLD; | ||
| + | MPI_Comm_size(comm, &comm_sz); | ||
| + | MPI_Comm_rank(comm, &my_rank); | ||
| + | |||
| + | //считываем размеры матрицы | ||
| + | int n,m; | ||
| + | if (my_rank == 0) { | ||
| + | n = strtol(argv[1], NULL, 10); | ||
| + | m = strtol(argv[2], NULL, 10); | ||
| + | } | ||
| + | |||
| + | MPI_Bcast(&m, 1, MPI_INT, 0, comm); | ||
| + | MPI_Bcast(&n, 1, MPI_INT, 0, comm); | ||
| + | |||
| + | //делим матрицу | ||
| + | int local_n = n / comm_sz; | ||
| + | int rem = n % comm_sz; | ||
| + | if(my_rank < rem) { | ||
| + | local_n++; | ||
| + | } | ||
| + | |||
| + | vector<vector<double> > G(local_n, vector<double> (m, -5)) , H(local_n, vector<double> (m, -5)); | ||
| + | |||
| + | //генирируем мартицу | ||
| + | srand(time(NULL)); | ||
| + | for(int i = 0; i < local_n; ++i) { | ||
| + | for(int j = 0; j < m; ++j) { | ||
| + | H[i][j] = rand(); | ||
| + | G[i][j] = rand(); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | double s_time = 0; | ||
| + | if (rank == 0) { | ||
| + | s_time = MPI_Wtime(); | ||
| + | } | ||
| + | |||
| + | //ищем максимум в G благожелательно к лидеру на каждую его стратегию | ||
| + | vector<int> local_ind(local_n); | ||
| + | vector<double> local_max(local_n); | ||
| + | for(int i = 0; i < local_n; ++i){ | ||
| + | double max_in_line = G[i][0]; | ||
| + | int ind_max = 0; | ||
| + | for(int j = 0; j < m; ++j){ | ||
| + | if (G[i][j] > max_in_line) { | ||
| + | max_in_line = G[i][j]; | ||
| + | ind_max = j; | ||
| + | } else if (G[i][j] == max_in_line) { | ||
| + | if (H[i][j] > H[i][ind_max]) { | ||
| + | ind_max = j; | ||
| + | max_in_line = G[i][j]; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | local_ind[i] = ind_max; | ||
| + | local_max[i] = H[i][ind_max]; | ||
| + | } | ||
| + | |||
| + | //ищем с учетом ответа второго наилучшую тратегию для лидера | ||
| + | double max_in_proc = local_max[0]; | ||
| + | for (int i = 0; i < local_n; ++i) { | ||
| + | if(max_in_proc < local_max[i]) { | ||
| + | max_in_proc = local_max[i]; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | double res_max; | ||
| + | |||
| + | MPI_Allreduce(&max_in_proc, &res_max, 1, MPI_DOUBLE, MPI_MAX, comm); | ||
| + | |||
| + | //ищем все равновесия по Штакельбергу | ||
| + | for (int i = 0; i < local_n; ++i) { | ||
| + | if(res_max == local_max[i]) { | ||
| + | //i, max_ind[i] равновесие по Штакельбергу | ||
| + | } | ||
| + | } | ||
| + | |||
| + | //выводим время | ||
| + | double f_time = 0; | ||
| + | if (rank == 0) { | ||
| + | f_time = MPI_Wtime(); | ||
| + | cout << n << ' ' << f_time - s_time << endl; | ||
| + | } | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | MPI_Finalize(); | ||
| + | |||
| + | } | ||
| + | </source> | ||
== Литература == | == Литература == | ||
Текущая версия на 00:44, 6 декабря 2017
Основные авторы описания: Закирова С.В. Поиск равновесия в дуополии Штакельберга
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Модель дуополии Штакельберга является развитием модели дуополии Курно. Если в модели Курно считается, что участники рынка не прогнозируют отклика конкурента на собственные действия, то в модели Штакельберга один участник рынка не прогнозирует поведения конкурента, а второй учитывает поведение первого, зная, что конкурент не ответит на его действия. Другими словами, второй участник рынка знает, что первый участник рынка ведет себя в соответствии с моделью Курно. [1]
1.2 Математическое описание алгоритма
Есть множество стратегий первого игрока [math] X [/math] и множество стратегий [math] Y [/math] второго игрока. Первым ходит игрок, называемый лидером, его стратегия [math] x \in X [/math]. Второй игрок, называемый подчиненным, ходит стратегией [math] y \in Y [/math]. У каждого игрока есть своя функция выигрыша. Для лидера это функция [math] H(x,y) [/math]. Для подчиненного [math] G(x,y) [/math]. Оба хотят максимизировать свой выигрыш, при условии лояльности(лояльность, это когда при условии одинакового выигрыша для второго, он максимизирует выигрыш первого) второго игрока по отношении к первому. Набор стратегий [math] (x^*,y^*) [/math] называется равновесием Штакельберга[2], если [math] y^* = R(x^*) [/math] есть наилучший ответ подчиненного на стратегию лидера, которая находится как решение задачи [math] H(x^*, y^*) = max H(x,R(x)) [/math] (максимум берется по всем стратегиям [math]x[/math] из [math]X[/math])
1.3 Вычислительное ядро алгоритма
Вычислительным ядром данного алгоритма является поиск максимума в строке. Таким образом мы находим наилучший ответ второго игрока.
1.4 Макроструктура алгоритма
Как уже сказано в пункте выше, основнуая составляющая часть алгоритма это поиск максимума в строке.
Алгоритм можно представить как многократное повторение(по количеству строк) поиска максимума в строках первой матрицы. После этого поиск максимума по элементам второй матрицы, индексы которых уже были найдены в первой итерации.
1.5 Схема реализации последовательного алгоритма
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
int main(int argc, char *argv[])
{
//считиываем m и n
int n = strtol(argv[1], NULL, 10);
int m = strtol(argv[2], NULL, 10);
//создаем матрицы G и H
vector<vector<double>> H(n, vector<double>(m));
vector<vector<double>> G(n, vector<double>(m));
//инициализируем матрицы G и H
srand(time(NULL));
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
H[i][j] = rand();
G[i][j] = rand();
}
}
//ищем максимум в G благожелательно к лидеру на каждую его стратегию
vector<int> ind(n);
for(int i = 0; i < n; ++i){
double max_in_line = H[i][0];
int ind_max = 0;
for(int j = 0; j < m; ++j){
if (G[i][j] > max_in_line) {
max_in_line = G[i][j];
ind_max = j;
} else if (G[i][j] == max_in_line) {
if (H[i][j] > H[i][ind_max]) {
ind_max = j;
max_in_line = G[i][j];
}
}
}
ind[i] = ind_max;
}
//ищем с учетом ответа второго наилучшую тратегию для лидера
int str_h = 0;
for(int i = 0; i < n; ++i) {
if (H[i][ind[i]] > H[str_h][ind[str_h]]) {
str_h = i;
}
}
}
1.6 Последовательная сложность алгоритма
Для первой части - поиска наилучших стратегий для воторого потребуется [math] m * n [/math] операций сравенения.
Для второй части - поиска наилучших стратегий первого потребуется [math] n [/math] операций сравнения.
Таким образом результирующая сложность алгоритма - [math] О(n * m) [/math] операций.
1.7 Информационный граф
Опишем граф алгоритма в виде рисунка.
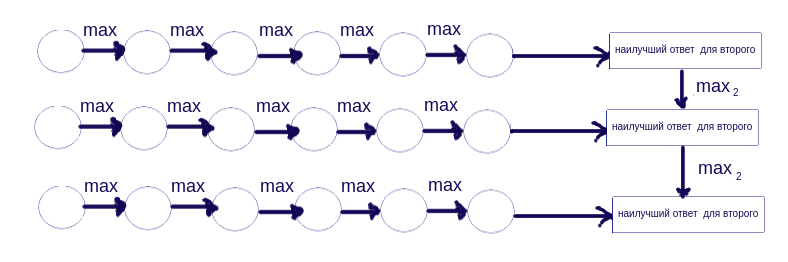
Круглые элеменеты графа - элементы матрицы G. Под max, имеется в виду функция поиска максимума в строке (причем с уметом благожелательности).
max2 - опять же функция поиска максимума для первого, исходя из ответов второго.
1.8 Ресурс параллелизма алгоритма
Каждую строку можно обрабатывать отдельным процессором. Таким образом каждый процессор бежит по строке и ищет там максимум (с условием благосклонности к лидеру). После этого процессоры синхронизируются и мы ищем максимум из уже найденых значений, таким образом мы получаем наибольший выигрыш для лидера, после чего находим все равновесия по Штакельбергу.
Параллельная сложность: [math]О(m)[/math], где [math]m[/math] число столбцов а нашей матрице.
1.9 Входные и выходные данные алгоритма
Входными данными являются пара матриц [math] H(x,y) [/math], [math] G(x,y) [/math] одинакового размера [math]n * m [/math] (стратегии обоих игроков). Выходные данные это множество пар чисел [math] (x^*,y^*) [/math], где каждая из пар является равновесием по Штакельбергу в нашей дуаполии.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Проведём исследование масштабируемости параллельной реализации алгоритма. Набор и границы значений изменяемых параметров запуска реализации алгоритма:
число процессоров [1,2 4, 8 : 32] со значениями квадрата целого числа;
размер матрицы(для тестов бралась квадратная матрица) [1000:10000] с шагом 1000.
На следующем рисунке приведен график производительности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.
сведения о программно-аппаратной среде
компьютер: суперкомпьютор Ломоносов
компилятор с использованными опциями оптимизации: mpicxx версии openmpi/1.8.4-gcc
библиотеки: #include <mpi.h>, #include <iostream>, #include <cstdlib>, #include <ctime>, #include <vector>
выводы о масштабируемости
Мы получили ожидаемые результаты(в целом), что производительность увеличивается с увеличеснием количества процессоров и уменьшается с увеличеннием количества строк. Это можно объяснить тем, что выбранный алгоритм очень хорошо распараллеливается, а «общение» процессоров почти не требуется (это важно так как эта процедура достаточно ресурсозатратна).
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Написанная мной, текущая реализация алгоритма:
#include <mpi.h>
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>
using namespace std;
int main(int argc, char * argv[])
{
int comm_sz, my_rank;
MPI_Init(&argc, &argv);
MPI_Comm comm = MPI_COMM_WORLD;
MPI_Comm_size(comm, &comm_sz);
MPI_Comm_rank(comm, &my_rank);
//считываем размеры матрицы
int n,m;
if (my_rank == 0) {
n = strtol(argv[1], NULL, 10);
m = strtol(argv[2], NULL, 10);
}
MPI_Bcast(&m, 1, MPI_INT, 0, comm);
MPI_Bcast(&n, 1, MPI_INT, 0, comm);
//делим матрицу
int local_n = n / comm_sz;
int rem = n % comm_sz;
if(my_rank < rem) {
local_n++;
}
vector<vector<double> > G(local_n, vector<double> (m, -5)) , H(local_n, vector<double> (m, -5));
//генирируем мартицу
srand(time(NULL));
for(int i = 0; i < local_n; ++i) {
for(int j = 0; j < m; ++j) {
H[i][j] = rand();
G[i][j] = rand();
}
}
double s_time = 0;
if (rank == 0) {
s_time = MPI_Wtime();
}
//ищем максимум в G благожелательно к лидеру на каждую его стратегию
vector<int> local_ind(local_n);
vector<double> local_max(local_n);
for(int i = 0; i < local_n; ++i){
double max_in_line = G[i][0];
int ind_max = 0;
for(int j = 0; j < m; ++j){
if (G[i][j] > max_in_line) {
max_in_line = G[i][j];
ind_max = j;
} else if (G[i][j] == max_in_line) {
if (H[i][j] > H[i][ind_max]) {
ind_max = j;
max_in_line = G[i][j];
}
}
}
local_ind[i] = ind_max;
local_max[i] = H[i][ind_max];
}
//ищем с учетом ответа второго наилучшую тратегию для лидера
double max_in_proc = local_max[0];
for (int i = 0; i < local_n; ++i) {
if(max_in_proc < local_max[i]) {
max_in_proc = local_max[i];
}
}
double res_max;
MPI_Allreduce(&max_in_proc, &res_max, 1, MPI_DOUBLE, MPI_MAX, comm);
//ищем все равновесия по Штакельбергу
for (int i = 0; i < local_n; ++i) {
if(res_max == local_max[i]) {
//i, max_ind[i] равновесие по Штакельбергу
}
}
//выводим время
double f_time = 0;
if (rank == 0) {
f_time = MPI_Wtime();
cout << n << ' ' << f_time - s_time << endl;
}
MPI_Finalize();
}