Участник:Nikkou/Фильтр Собеля: различия между версиями
Nikkou (обсуждение | вклад) (Новая страница: «Описание параллельной реализации алгоритма фильтрации Собеля. Автор: А.Г.Лыжов (401 групп…») |
Nikkou (обсуждение | вклад) |
||
| (не показано 15 промежуточных версий этого же участника) | |||
| Строка 22: | Строка 22: | ||
Это матрицы такого же размера, как исходное изображение, так как параметры градиента вычисляются для каждого пикселя изображения. | Это матрицы такого же размера, как исходное изображение, так как параметры градиента вычисляются для каждого пикселя изображения. | ||
| − | Промежуточные горизонтальные и вертикальные производные вычисляются с помощью следующих двумерных сверток: | + | Промежуточные горизонтальные и вертикальные производные (а точнее, их аппроксимации) вычисляются с помощью следующих двумерных сверток: |
<math> | <math> | ||
| Строка 48: | Строка 48: | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| + | Макроструктуру в основном составляют: | ||
| + | |||
| + | 1) двумерные свертки, приведенные в математическом описании; | ||
| + | |||
| + | 2) операция поэлементного геометрического среднего между промежуточными аппроксимациями. | ||
| + | |||
| + | Эти элементы алгоритма приведены в разделе с математическим описанием. | ||
| + | |||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| + | Запись на C++-подобном псевдокоде: | ||
| + | <pre>float *sobel(float *img) { | ||
| + | // Оператор собеля разложим на одномерные свертки с ядрами [1, 0, -1] и [1, 2, 1] | ||
| + | // Здесь они обозначены как соответственно diff_kernel и sum_kernel | ||
| + | horiz_der = conv(img, diff_kernel, sum_kernel); // Аппроксимация производной по горизонтальному направлению | ||
| + | vert_der = conv(img, sum_kernel, diff_kernel); // Аппроксимация производной по вертикальному направлению | ||
| + | return combine_horiz_vert(horiz_der, vert_der); | ||
| + | } | ||
| + | |||
| + | for (int i = 0; i < n_images; i++) { | ||
| + | img = get_input(i); // Чтение изображения с диска | ||
| + | res = sobel(img); | ||
| + | write_result(res); // Запись результата на диск | ||
| + | }</pre> | ||
| + | |||
| + | Для повышения производительности в последовательной реализации всегда следует использовать сепарабельность свертки и считать двумерную свертку как композицию из одномерных. | ||
| + | |||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | <math>O(M\cdot N \cdot K)</math> при обработке K изображений размером M*N, так как все макроэлементы, составляющие структуру алгоритма, выполняются за константу для одного пикселя. | ||
| + | |||
=== Информационный граф === | === Информационный граф === | ||
| + | [[Файл:Graph.png]] | ||
| + | |||
| + | Группы вершин: | ||
| + | |||
| + | 1) выполняет операцию чтения изображения с диска. Количество вершин равно количеству изображений K. | ||
| + | |||
| + | 2) выполняет горизонтальную свертку каждого изображения. | ||
| + | |||
| + | 3) выполняет вертикальную свертку каждого изображения. | ||
| + | |||
| + | 4) комбинирует частичные результаты. | ||
| + | |||
| + | 5) записывает результат на диск. | ||
| + | |||
| + | Группы вершин в графе соединены последовательно, и каждая вершина соединена только с вершинами соседних групп, соответствующих одному и тому же изображению. | ||
| + | |||
| + | Граф альтернативно можно представить и более детально, например, раскрыв макрооперации сверток изображения по строкам, столбцам, элементам ядер. | ||
| + | |||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | Группы параллельных ветвей: | ||
| + | |||
| + | 1) Операции над разными изображениями независимы и образуют массово параллельные ветви. | ||
| + | |||
| + | 2) Одномерные свертки в разложении двумерной могут считаться независимо. Это конечный параллелизм. | ||
| + | |||
| + | 3) Одномерные свертки можно считать независимо по каждому пикселю - массовый параллелизм. Можно сделать их вычисление параллельным на практике если и не по пикселям, то по крайней мере по специально сконструированным блокам изображения для оптимального выполнения на GPU. | ||
| + | |||
| + | В предположении неограниченной доступности вычислительных узлов алгоритм выполняется за константное время. Последовательными операциями в таком случае являются только чтение, подсчет сверток по направлениям, их комбинация и запись результата на диск. | ||
| + | |||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| + | Входные данные: K вещественных матриц размером N*M с диапазоном значений от 0 до 1. О структуре данных нельзя делать предположений. | ||
| + | Выходные данныые: K вещественных матриц размером N*M. Дополнительно можно отнормировать диапазон значений результата для визуализации. | ||
| + | |||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| Строка 65: | Строка 123: | ||
==== Масштабируемость алгоритма ==== | ==== Масштабируемость алгоритма ==== | ||
==== Масштабируемость реализации алгоритма ==== | ==== Масштабируемость реализации алгоритма ==== | ||
| + | При обилии входных данных очень легко распределить различные изображения на различные процессы. Но при параллельной обработке одного изображения возникают тонкости, связанные с барьерными синхронизациями между операциями, эффективным использованием быстрой памяти и "разогревом" GPU. | ||
| + | |||
| + | В целом значительных препятствий для распараллеливания нет, что можно видеть по графику слабой масштабируемости. | ||
| + | |||
| + | График сильной масштабируемости: | ||
| + | |||
| + | [[Файл:Strong.PNG]] | ||
| + | |||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | В силу возможности эффективно распараллелить фильтрацию с ядром Собеля и широких возможностей практического применения, есть | ||
| + | |||
| + | - последовательные реализации (OpenCV) | ||
| + | |||
| + | - параллельные реализации на CUDA для GPU: [https://github.com/JoeLoser/Sobel-Filter-CUDA 1], [https://github.com/JakubDziworski/Cuda-Sobel 2] | ||
| + | |||
| + | - параллельная реализация на MPI для CPU: [https://github.com/cnavarropalos/sobel-mpi ссылка]. | ||
| + | |||
| + | Автор статьи написал параллельную реализацию, которая использует и MPI для распределения входных данных по GPU на узлах, и CUDA для эффективного просчета на GPU. За основу был взят [https://github.com/phrb/intro-cuda/tree/master/src/cuda-samples/3_Imaging/convolutionSeparable код примера эффективной реализации сепарабельной двумерной свертки над CUDA] от NVIDIA. | ||
== Литература == | == Литература == | ||
| + | |||
| + | Podlozhnyuk, V. (2007). Image convolution with CUDA. NVIDIA Corporation white paper, June, 2097(3). | ||
| + | |||
| + | Ogawa, K., Ito, Y., & Nakano, K. (2010, November). Efficient Canny edge detection using a GPU. In Networking and Computing (ICNC), 2010 First International Conference on (pp. 279-280). IEEE. | ||
| + | |||
| + | Luo, Y., & Duraiswami, R. (2008, June). Canny edge detection on NVIDIA CUDA. In Computer Vision and Pattern Recognition Workshops, 2008. CVPRW'08. IEEE Computer Society Conference on (pp. 1-8). IEEE. | ||
[[Категория:Начатые статьи]] | [[Категория:Начатые статьи]] | ||
Текущая версия на 11:48, 8 декабря 2017
Описание параллельной реализации алгоритма фильтрации Собеля.
Автор: А.Г.Лыжов (401 группа).
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Фильтр Собеля - дискретный дифференциальный оператор, который используется для приближения градиента яркости изображения. Он часто используется в алгоритмах выделения границ при обработке изображений. Фильтр Собеля был предложен Ирвином Собелем и Гэри Фелдманом в лаборатории искусственного интеллекта Стэнфорда в 1968.
Фильтр Собеля легко вычислять, так как он основан на свертках изображения с небольшими ядрами. Из-за этого он аппроксимирует градиент со значительной погрешностью, но качество аппроксимации оказывается достаточным для многих практических приложений.
1.2 Математическое описание алгоритма
Исходные данные:
- изображение [math]A^{N\cdot M}[/math]
Вычисляемые данные:
- матрица аппроксимации модуля градиента [math]G^{N\cdot M}[/math]
- матрица аппроксимации направления градиента [math]\Theta^{N\cdot M}[/math]
Это матрицы такого же размера, как исходное изображение, так как параметры градиента вычисляются для каждого пикселя изображения.
Промежуточные горизонтальные и вертикальные производные (а точнее, их аппроксимации) вычисляются с помощью следующих двумерных сверток:
[math] \mathbf{G}_x = \begin{bmatrix} +1 & 0 & -1 \\ +2 & 0 & -2 \\ +1 & 0 & -1 \end{bmatrix} * \mathbf{A} ,\ \mathbf{G}_y = \begin{bmatrix} +1 & +2 & +1\\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix} * \mathbf{A} [/math]
Аппроксимации для модуля и направления градиента можно получить, скомбинировав эти производные:
[math]\mathbf{G} = \sqrt{ {\mathbf{G}_x}^2 + {\mathbf{G}_y}^2 }[/math]
[math]\mathbf{\Theta} = \operatorname{atan}\left({ \mathbf{G}_y \over \mathbf{G}_x }\right)[/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро совпадает с алгоритмом, так как все описанные операции выполняются за [math]O(M\cdot N)[/math] на одном изображении.
1.4 Макроструктура алгоритма
Макроструктуру в основном составляют:
1) двумерные свертки, приведенные в математическом описании;
2) операция поэлементного геометрического среднего между промежуточными аппроксимациями.
Эти элементы алгоритма приведены в разделе с математическим описанием.
1.5 Схема реализации последовательного алгоритма
Запись на C++-подобном псевдокоде:
float *sobel(float *img) {
// Оператор собеля разложим на одномерные свертки с ядрами [1, 0, -1] и [1, 2, 1]
// Здесь они обозначены как соответственно diff_kernel и sum_kernel
horiz_der = conv(img, diff_kernel, sum_kernel); // Аппроксимация производной по горизонтальному направлению
vert_der = conv(img, sum_kernel, diff_kernel); // Аппроксимация производной по вертикальному направлению
return combine_horiz_vert(horiz_der, vert_der);
}
for (int i = 0; i < n_images; i++) {
img = get_input(i); // Чтение изображения с диска
res = sobel(img);
write_result(res); // Запись результата на диск
}
Для повышения производительности в последовательной реализации всегда следует использовать сепарабельность свертки и считать двумерную свертку как композицию из одномерных.
1.6 Последовательная сложность алгоритма
[math]O(M\cdot N \cdot K)[/math] при обработке K изображений размером M*N, так как все макроэлементы, составляющие структуру алгоритма, выполняются за константу для одного пикселя.
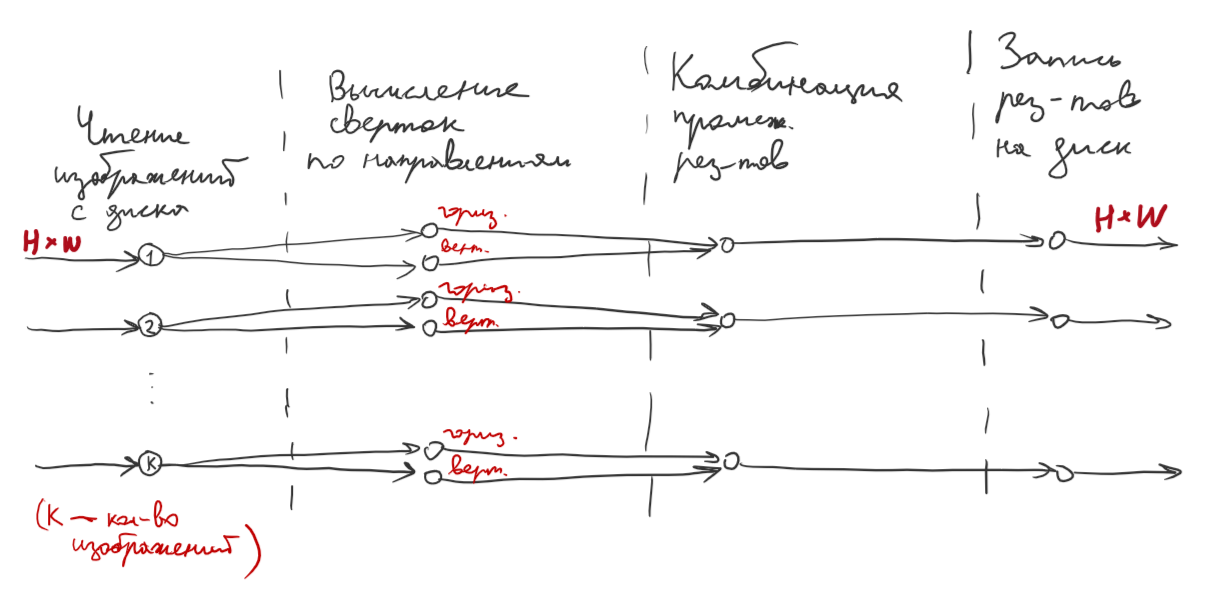
1.7 Информационный граф
Группы вершин:
1) выполняет операцию чтения изображения с диска. Количество вершин равно количеству изображений K.
2) выполняет горизонтальную свертку каждого изображения.
3) выполняет вертикальную свертку каждого изображения.
4) комбинирует частичные результаты.
5) записывает результат на диск.
Группы вершин в графе соединены последовательно, и каждая вершина соединена только с вершинами соседних групп, соответствующих одному и тому же изображению.
Граф альтернативно можно представить и более детально, например, раскрыв макрооперации сверток изображения по строкам, столбцам, элементам ядер.
1.8 Ресурс параллелизма алгоритма
Группы параллельных ветвей:
1) Операции над разными изображениями независимы и образуют массово параллельные ветви.
2) Одномерные свертки в разложении двумерной могут считаться независимо. Это конечный параллелизм.
3) Одномерные свертки можно считать независимо по каждому пикселю - массовый параллелизм. Можно сделать их вычисление параллельным на практике если и не по пикселям, то по крайней мере по специально сконструированным блокам изображения для оптимального выполнения на GPU.
В предположении неограниченной доступности вычислительных узлов алгоритм выполняется за константное время. Последовательными операциями в таком случае являются только чтение, подсчет сверток по направлениям, их комбинация и запись результата на диск.
1.9 Входные и выходные данные алгоритма
Входные данные: K вещественных матриц размером N*M с диапазоном значений от 0 до 1. О структуре данных нельзя делать предположений. Выходные данныые: K вещественных матриц размером N*M. Дополнительно можно отнормировать диапазон значений результата для визуализации.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
При обилии входных данных очень легко распределить различные изображения на различные процессы. Но при параллельной обработке одного изображения возникают тонкости, связанные с барьерными синхронизациями между операциями, эффективным использованием быстрой памяти и "разогревом" GPU.
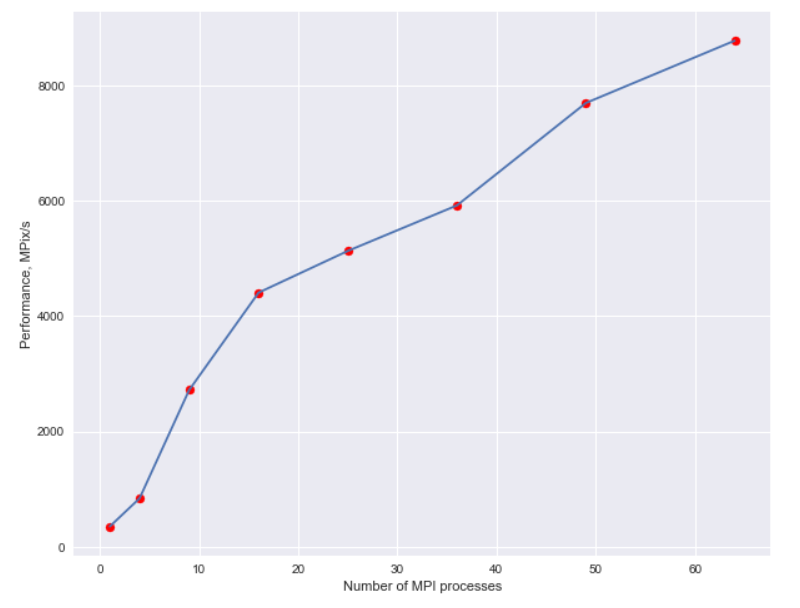
В целом значительных препятствий для распараллеливания нет, что можно видеть по графику слабой масштабируемости.
График сильной масштабируемости:
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В силу возможности эффективно распараллелить фильтрацию с ядром Собеля и широких возможностей практического применения, есть
- последовательные реализации (OpenCV)
- параллельные реализации на CUDA для GPU: 1, 2
- параллельная реализация на MPI для CPU: ссылка.
Автор статьи написал параллельную реализацию, которая использует и MPI для распределения входных данных по GPU на узлах, и CUDA для эффективного просчета на GPU. За основу был взят код примера эффективной реализации сепарабельной двумерной свертки над CUDA от NVIDIA.
3 Литература
Podlozhnyuk, V. (2007). Image convolution with CUDA. NVIDIA Corporation white paper, June, 2097(3).
Ogawa, K., Ito, Y., & Nakano, K. (2010, November). Efficient Canny edge detection using a GPU. In Networking and Computing (ICNC), 2010 First International Conference on (pp. 279-280). IEEE.
Luo, Y., & Duraiswami, R. (2008, June). Canny edge detection on NVIDIA CUDA. In Computer Vision and Pattern Recognition Workshops, 2008. CVPRW'08. IEEE Computer Society Conference on (pp. 1-8). IEEE.