Стандарт визуализации ГА: различия между версиями
| [выверенная версия] | [выверенная версия] |
| Строка 41: | Строка 41: | ||
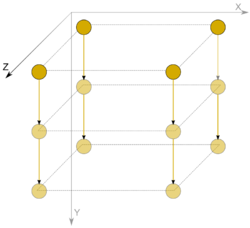
* Первый предлагаемый метод отображения ярусно-параллельной формы - построение набора последовательных изображений графа алгоритма, на каждом из которых некоторым образом, например, насыщенностью цвета, выделен ярус ГА, соответствующий номеру изображения в наборе. | * Первый предлагаемый метод отображения ярусно-параллельной формы - построение набора последовательных изображений графа алгоритма, на каждом из которых некоторым образом, например, насыщенностью цвета, выделен ярус ГА, соответствующий номеру изображения в наборе. | ||
| − | [[Файл:Dense mtrx product layer1.png|250px|thumb|center|Пример отображения графа алгоритма в ярусно-параллельной форме с помощью набора изображений - выделен первый ярус.]][[Файл:Dense mtrx product layer2.png|250px|thumb|center|Пример отображения графа алгоритма в ярусно-параллельной форме с помощью набора изображений - выделен второй ярус.]] | + | [[Файл:Dense mtrx product layer1.png|250px|thumb|center|Пример отображения графа алгоритма в ярусно-параллельной форме с помощью набора изображений - выделен первый ярус.]] |
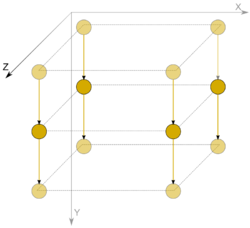
| + | [[Файл:Dense mtrx product layer2.png|250px|thumb|center|Пример отображения графа алгоритма в ярусно-параллельной форме с помощью набора изображений - выделен второй ярус.]] | ||
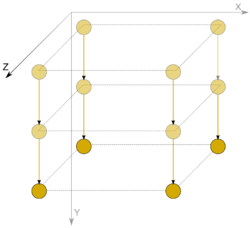
| + | [[Файл:Dense mtrx product layer3.png|250px|thumb|center|Пример отображения графа алгоритма в ярусно-параллельной форме с помощью набора изображений - выделен третий ярус.]] | ||
* Второй способ - построение отдельного изображения графа алгоритма, на котором все вершины, соответствующие одному ярусу, объединены в отдельный кластер. Рекомендуется в этом случае использовать предложенную схему визуализации с трёхмерной декартовой системой координат - тогда логично расположить на одной плоскости вершины, соответствующие одному ярусу. | * Второй способ - построение отдельного изображения графа алгоритма, на котором все вершины, соответствующие одному ярусу, объединены в отдельный кластер. Рекомендуется в этом случае использовать предложенную схему визуализации с трёхмерной декартовой системой координат - тогда логично расположить на одной плоскости вершины, соответствующие одному ярусу. | ||
Версия 17:55, 5 ноября 2015
Каждый алгоритм, о котором рассказывается на страницах этой вики согласно предлагаемой авторами проекта схеме, содержит в своём описании пункт под названием "Информационный граф". Данное руководство представляет собой набор правил, в соответствии с которыми рекомендуется изображать граф алгоритма при заполнении этого пункта описания. Поскольку авторы проекта ставят своей целью описание произвольных алгоритмов по единой схеме, эти правила направлены на построение изображений графа алгоритма в едином, узнаваемом стиле, который был бы прост для восприятия. В рамках этого руководства под словами "Визуализация алгоритма" понимается совокупность всех изображений, пояснений к ним и возможной дополнительной информации, обеспечивающая удовлетворительное наполнение вышеозначенного пункта описания алгоритма.
Содержание
1 Необходимый минимум изображений и описаний
- Визуализация алгоритма должна состоять как минимум из одного изображения , содержащего граф алгоритма.
- Граф алгоритма на этом изображении рекомендуется представлять для частного случая алгоритма, то есть для фиксированного объёма входных данных и однозначного выбора версии алгоритма в тех его частях, где возможна некоторая вариативность ( например, нахождение равномерной нормы вектора с экономией вызовов функции максимума или без неё ). Однако этот частный случай должен давать полное представление о структуре алгоритма и его характерных особенностях. ГА имеет потенциально бесконечный размер, но графы одного алгоритма для разных объёмов входных данных, как правило, имеют одну и ту же структуру и различаются лишь масштабами, поэтому в качестве частного случая рекомендует выбрать ГА для небольшого объёма входных данных, так как малые изображения проще для восприятия.
- Визуализация не должна содержать графов, не имеющих отношения к описываемому алгоритму. Также не рекомендуется включать в визуализацию графы, не соответствующие определению графа алгоритма ( Граф алгоритма - ориентированный граф, состоящий из вершин, соответствующих операциям алгоритма, и направленных дуг, соответствующих передаче данных между ними ), за исключением возможных форм представления ГА и его видоизменений, описанных в последующих пунктах. Приветствуются пояснения, дающие дополнительную информацию о структуре графа, например, информацию о вычислительной сложности отдельных вершин графа алгоритма или оси декартовой системы координат, помогающие понять взаимное расположение вершин графа алгоритма.
2 Особенности изображения ГА
2.1 Структурная схема визуализации ГА
- В качестве инструмента визуализации может быть использован любой редактор векторной графики, например CorelDRAW, Inkscape и им подобные. Финальные версии построенных схем визуализации можно публиковать в виде изображений любого формата, поддерживаемого движком MediaWiki.
- Вершины графа обозначаются кругами, размер которых должен совпадать для всех операций одного вида. Требований к относительному размеру вершин, соответствующих разным операциям, нет, но рекомендуется обозначать крупнее вершины, соответствующие макроблокам либо вызовам процедур, а все базовые операции обозначать вершинами одного размера.
- Каждая вершина графа должна быть помечена некоторым текстом, обозначающим операцию, соответствующую этой вершине, и одинаковым для всех вершин, содержащих одну и ту же операцию. В случае наличия дополнительных изображений с разъяснением структуры операций, соответствующим этой операции текстом помечаются и поясняющие изображения.
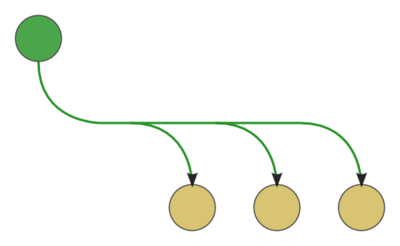
- Дуги графа обозначаются линиями со стрелками на концах, соответствующих "адресату" данных. Возможно использование одной линии с ответвлениями для изображения рассылки данных от одной вершины нескольким. В этом случае такая "магистраль" данных должна иметь на изображении большую толщину, нежели одиночные пересылки. Аналогично, допускается та же техника для изображения пересылки результатов нескольких операций для одной операции.
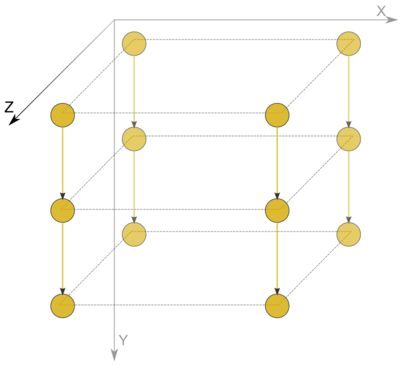
- Рекомендуется использовать следующую общую схему визуализации ГА: ввести трёхмерную декартову систему координат, а также набор плоскостей, параллельных одной из координатных, например oXZ. На каждой такой плоскости вводится одна и та же равномерная сетка, после чего все вершины ГА располагаются на этих плоскостях в узлах сетки.
2.2 Цветовая схема визуализации ГА
- Одинаковые по смыслу и структуре операции рекомендуется обозначать одним цветом вне зависимости от входных данных. Разные операции обозначаются разными цветами, опять же независимо от входных данных.
- Выбор цветовой палитры остаётся за тем, кто строит конкрентную визуализацию. В случае построения псевдотрёхмерного изображения, рекомендуется использовать полупрозрачные цвета, чтобы исключить перекрытие обзора вершин, наиболее удаленных от пользователя.
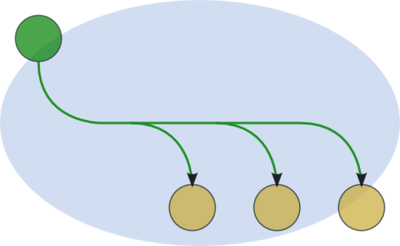
- В случае наличия дополнительных изображений, поясняющих структуру конкретных операций в графе алгоритма, задний фон этих изображений предлагается представлять в виде эллипаса того же цвета, каким обозначается операция в исходном графе алгоритма.
- Цвет любой дуги графа рекомендуется задавать в соответствии с цветом вершины операции, из которой выходит эта дуга.
- Если используется методика псевдотрёхмерного отображения графа алгоритма ( возможно, с использованием трёхмерной декартовой системы коордитнат ), то набор плоскостей графа алгоритма рекомендуется изображать с использованием цветов разной насыщенности для разных плоскостей графа и одной насыщенности для всех вершин и дуг, расположенных на одном слое. Приветствуется использование градиентной окраски дуг, соединяющих вершины на разных слоях.
2.3 Построение ярусно-параллельной формы ГА
- Первый предлагаемый метод отображения ярусно-параллельной формы - построение набора последовательных изображений графа алгоритма, на каждом из которых некоторым образом, например, насыщенностью цвета, выделен ярус ГА, соответствующий номеру изображения в наборе.
- Второй способ - построение отдельного изображения графа алгоритма, на котором все вершины, соответствующие одному ярусу, объединены в отдельный кластер. Рекомендуется в этом случае использовать предложенную схему визуализации с трёхмерной декартовой системой координат - тогда логично расположить на одной плоскости вершины, соответствующие одному ярусу.
2.4 Визуализация входных и выходных данных алгоритма
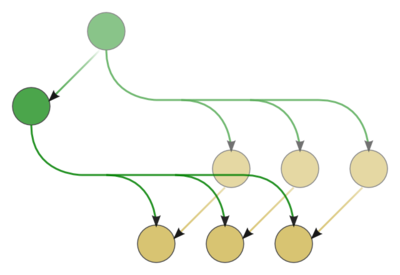
- Поскольку сам ГА по определению не содержит информации о входных и выходных данных алгоритма, удобно дополнить визуализацию надграфом ГА, который отображает так же входные и выходные данные в алгоритме.
- Вершины, соответствующие входным и выходным данным, отображаются иными геометрическими фигурами ( например, квадратами ), в остальном правила и рекомендации по визуализации аналогичны таковым для самого ГА.
3 Методы визуализации сложных алгоритмов
3.1 Многомерные алгоритмы
Размерностью алгоритма в контексте этого пункта будем называть максимальную вложенность операций, встречающуюся в алгоритме.
Более чем трёхмерные структуры трудны для восприятия именно как структуры в n-мерном пространстве. Поэтому многомерная структура конкретного алгоритма воспринимается как трёхмерная, что ведёт к непониманию того , как именно работает приведенный алгоритм. Для решения проблемы предлагается следующий набор правил визуализации.
- Многомерные структуры удобно воспринимать в качестве некой иерархии, где любая n – k -мерная гиперплоскость в исходном n-мерном пространстве представляется как единый макроблок, то есть n-мерная структура сводится к k-мерной структуре из макроблоков, где k <= 3. Далее каждый макроблок, представляющий собой n-k мерное пространство, аналогично разбивается на гиперплоскости. Процесс продолжается, пока n-k > 3. k на каждом шаге выбирается равным 1-3 в зависимости от структуры собственно алгоритма.
- В визуализации алгоритма не используется изображение графа алгоритма в полном виде. Вместо этого исходный граф алгоритма представляется в виде типовых макроблоков в качестве вершин графа алгоритма. Каждый макроблок опять же изображается в виде графа алгоритма в соответствии с построенной на предыдущем этапе иерархической структурой, пока не будет достигнут уровень базовых вычислительных операций. Таким образом , получается набор изображений. Кроме того, на каждом этапе решается проблема большого числа дуг в графе алгоритма по методу, описанному пунктом выше.
3.2 Алгоритмы с множественными связями
Иначе выражаясь, большое количество дуг в графе алгоритма. Основная возникающая при этом визуальная проблема — дуги перекрывают друг друга и определение того, каким вершинам инцидентна конкретная дуга, становится затруднительным. Для решения этой проблемы используется следующая методика, основанная на предположении о использовании для визуализации предложенной схемы с трёхмерной декартовой системой координат.
- Изображается проекция графа на плоскость Oxz в предположении, что вершины на разных параллельных плоскостях, соответствующие характерным блокам операций, имеют одинаковые значения ординат и аппликат.
- Вершины графа алгоритма в трёхмерной модели распологаются так, чтобы сохранилось распложение относительно Oxz и при этом образовался аналогичный набор параллельных плоскостей относительно плоскости Oyz.
- Изображается аналогичная проекция на плоскость Oyz.
- В графе алгоритма выделяются характерные по своей структуре блоки, которые изображаются отдельно с индексацией вершин, позволяющей определить, как именно этот блок расположен в графе алгоритма.
- Все полученные дополнительные изображения включаются в визуализацию алгоритма.