Сети сортировки: различия между версиями
| [непроверенная версия] | [выверенная версия] |
Lira (обсуждение | вклад) |
Lira (обсуждение | вклад) |
||
| (не показано 11 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | == Свойства и структура алгоритма == |
| − | === | + | === Общее описание алгоритма === |
| − | '''Сети сортировки''' используются для | + | '''Сети сортировки''' используются для упорядочивания больших массивов данных с помощью многопроцессорных вычислительных систем. Использование многопроцессорных систем, в ом числе с распределенной оперативной памятью, позволяет достигнуть двух основных целей: 1) снизить время выполнения сортировки; 2) благодаря использованию систем с распределенной оперативной памятью снять ограничение на размер обрабатываемого массива, за счет использования совокупной оперативной памяти всех вычислительных узлов. |
| − | расписание, обеспечивающее | + | Каждая сеть сортировки задаёт расписание, обеспечивающее согласованную параллельную работу нескольких процессоров над общей задачей упорядочивания множества элементов массива. Сети сортировки неэффективны, с точки зрения последовательного выполнения, но обеспечивают эффективную параллельную сортировку. Можно выделить масштабируемые сети сортировки, правила создания которых известны для произвольного числа процессоров, и немасштабируемые сети, предназначенные для выполнения только на вычислительных системах некоторых фиксированных размеров. |
| − | К первым следует отнести [[сеть сортировки простой вставкой]], [[сеть | + | К первым следует отнести [[сеть сортировки простой вставкой]], [[сеть нечетно-четной перестановки]], [[сеть четно-нечетного слияния Бетчера]] и [[сеть битонной сортировки]]. Среди немасштабируемых известны [[оптимальные сети сортировки| оптимальных]], с точки зрения времени выполнения сортировки, сетей для 6, 10 элементов<ref>Кнут Д.Э. Искусство программирования. – Т.3. – Сортировка и поиск 2-е изд.: Пер. с английского – М.: Вильямс, 2001. – 824 с.</ref>, а так же наилучшие из известных сегодня сетей для 12 и 16 элементов. |
| − | === Математическое описание === | + | === Математическое описание алгоритма === |
| − | Исходные данные: одномерный массив <math>n</math> | + | Исходные данные: одномерный массив <math>A</math>, содержащий <math>n</math> элементов, <math>|A|=n</math>. |
| − | Вычисляемые данные: упорядоченный массив. | + | Вычисляемые данные: упорядоченный массив <math>B=sort(A)</math>. |
| − | Постановка задачи | + | ==== Постановка задачи ==== |
''Сортировкой'', или упорядочиванием элементов, называется процесс их расположения согласно определенному линейному отношению порядка, такому как отношение «меньше или равно» для чисел. | ''Сортировкой'', или упорядочиванием элементов, называется процесс их расположения согласно определенному линейному отношению порядка, такому как отношение «меньше или равно» для чисел. | ||
Если не оговорено иное, будем считать, что сортировка выполняется на вычислительной системе с распределенной памятью. Данное предположение, благодаря потенциальной возможности обработки произвольно большого набора данных, существенно расширяет область применимости рассматриваемых методов. | Если не оговорено иное, будем считать, что сортировка выполняется на вычислительной системе с распределенной памятью. Данное предположение, благодаря потенциальной возможности обработки произвольно большого набора данных, существенно расширяет область применимости рассматриваемых методов. | ||
| − | + | Без ограничения общности рассмотрим задачу расположения <math>n</math> элементов массива в порядке неубывания. | |
| + | Пусть <math>B^i</math> – <math>i</math>-ый элемент массива <math>B</math>. | ||
| + | Тогда, массив <math>B</math> упорядочен, если выполняется соотношение<nowiki>:</nowiki> | ||
| − | + | <math>B^i\le B^j</math> , для любых допустимых <math>i,j</math>, при <math>i \lt j</math>. | |
| − | + | Уточним, что будет пониматься под упорядоченным массивом в том случае, когда его части распределены по нескольким процессорам. Пусть элементы массива распределены по процессорам некоторыми порциями <math>B_i</math>, <math>B=\bigcup\limits_{i} B_i</math>. | |
| − | <math>B_i^k | + | Пусть <math>B_i^k</math> – <math>k</math>-ый элемент <math>i</math>-го фрагмента массива <math>B</math> (фрагмента, расположенного на процессоре <math>i</math>). |
| − | + | Тогда, массив <math>B</math> упорядочен, если выполняются следующие соотношения<nowiki>:</nowiki> | |
| − | + | <math>B_i^k\le B_i^j</math> , для любых <math>i</math>, при <math>k \lt j</math>, | |
| − | |||
| − | + | <math>B_i^k\le B_l^j</math> , для любых <math>k,j</math>, при <math>i \lt l</math>. | |
| + | |||
| + | Пусть число используемых процессоров равно <math>p</math>. Будем предполагать, что исходный массив <math>A</math> распределен по процессорам некоторыми порциями <math>A_i</math>, где <math>0 \le i \le p-1</math> – номер процессора, <math>A=\bigcup\limits_{i} A_i</math>. | ||
| + | Потребуем, чтобы размеры всех порций были одинаковы<nowiki>:</nowiki> <math>|A_i|=|A_j|, |A_i|=|B_i|</math>, для любых <math>i,j</math>. Как будет показано ниже, только при выполнении этого условия, рассматриваемые параллельные алгоритмы, основанные на сетях сортировки, дают верный результат для любого исходного расположения элементов массива <math>A</math>. В случае, если число элементов сортируемого массива не делится нацело на число процессоров, можно дополнить исходный массив фиктивными элементами, исключив их после окончания сортировки. | ||
| + | |||
| + | ==== Временные материалы (в таком виде их не следует включать) ==== | ||
| + | |||
| + | Можно указать три больших класса последовательных алгоритмов сортировки, отличающихся [[оценкой вычислительной сложности]] (видом зависимости числа выполняемых операций от размера массива). Алгоритмы сортировки, основанные на сравнении элементов, имеют сложность порядка <math>O(n^2)</math> операций, где <math>n</math> – число сортируемых элементов, что неприемлемо при больших значениях n, либо <math>O(n log_2(n))</math> операций. Эти методы отличаются универсальностью. Последние из них взяты за основу «наилучшего» последовательного алгоритма сортировки. Известны методы поразрядной сортировки, обеспечивающие выполнение сортировки за <math>O(nk)</math> операций, где <math>k</math> – разрядность сортируемых данных, но их реализация существенно зависит от типа сортируемых данных, в связи с чем далее они не рассматриваются. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | === | + | |
| + | Рассмотрим ряд сетей сортировки в предположении, что на каждой линии сети расположен ровно один элемент массива: <math>n = p</math>: | ||
| + | |||
| + | [[сеть сортировки простой вставкой]] | ||
| + | |||
| + | [[сеть нечетно-четной перестановки]] | ||
| + | |||
| + | [[сеть четно-нечетного слияния Бетчера]] | ||
| + | |||
| + | [[сеть битонной сортировки]] | ||
| + | |||
| + | === Макроструктура алгоритма === | ||
| + | === Схема реализации последовательного алгоритма === | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
=== Информационный граф === | === Информационный граф === | ||
| − | === | + | === Ресурс параллелизма алгоритма === |
| − | === | + | === Входные и выходные данные алгоритма === |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | == Программная реализация == | + | |
| + | == Программная реализация алгоритма == | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | === | + | === Локальность данных и вычислений === |
| − | ==== | + | ==== Локальность реализации алгоритма ==== |
| − | + | ===== Структура обращений в память и качественная оценка локальности ===== | |
| − | ===== | ||
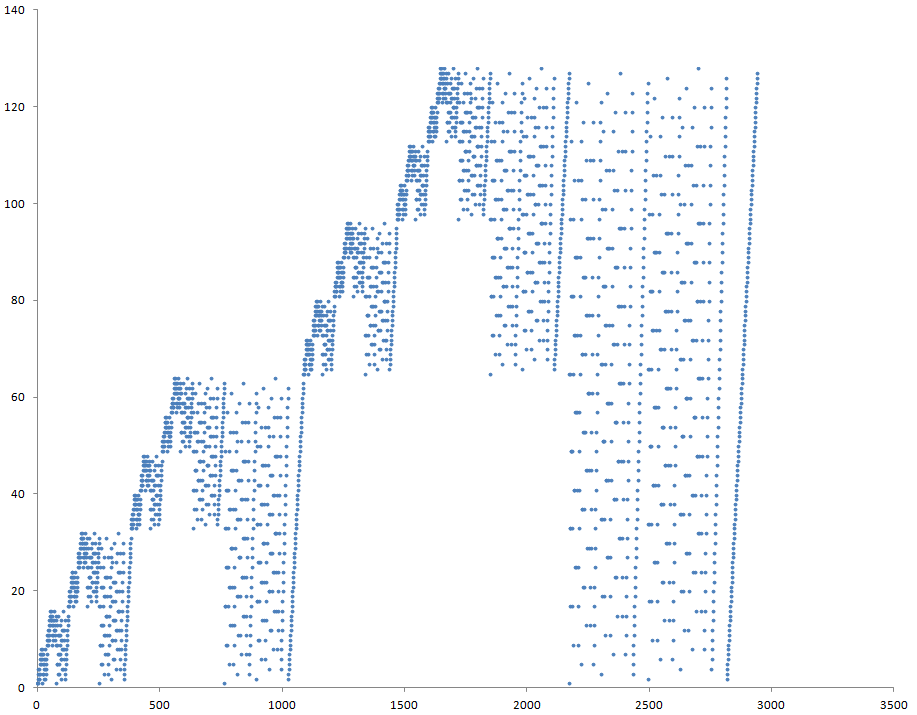
[[Файл:Sort01.png|thumb|center|1110px|Профиль доступа к памяти]] | [[Файл:Sort01.png|thumb|center|1110px|Профиль доступа к памяти]] | ||
| − | + | === Возможные способы и особенности параллельной реализации алгоритма === | |
| − | |||
| − | === Возможные способы и особенности реализации | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| − | ==== | + | ==== Масштабируемость алгоритма ==== |
| − | ==== | + | ==== Масштабируемость реализации алгоритма ==== |
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | |||
== Литература == | == Литература == | ||
| − | + | <references /> | |
| + | |||
| + | |||
# Седжвик Роберт. Фундаментальные алгоритмы на С++. Анализ/Структуры данных/Сортировка/Поиск: Пер. с англ./Роберт Седжвик. - СПб.: ООО "ДиаСофтЮП", 2002.-688с. | # Седжвик Роберт. Фундаментальные алгоритмы на С++. Анализ/Структуры данных/Сортировка/Поиск: Пер. с англ./Роберт Седжвик. - СПб.: ООО "ДиаСофтЮП", 2002.-688с. | ||
| + | |||
| + | |||
| + | [[Категория:Начатые статьи]] | ||
| + | [[Категория:Алгоритмы сортировки]] | ||
Текущая версия на 21:50, 9 мая 2019
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Сети сортировки используются для упорядочивания больших массивов данных с помощью многопроцессорных вычислительных систем. Использование многопроцессорных систем, в ом числе с распределенной оперативной памятью, позволяет достигнуть двух основных целей: 1) снизить время выполнения сортировки; 2) благодаря использованию систем с распределенной оперативной памятью снять ограничение на размер обрабатываемого массива, за счет использования совокупной оперативной памяти всех вычислительных узлов. Каждая сеть сортировки задаёт расписание, обеспечивающее согласованную параллельную работу нескольких процессоров над общей задачей упорядочивания множества элементов массива. Сети сортировки неэффективны, с точки зрения последовательного выполнения, но обеспечивают эффективную параллельную сортировку. Можно выделить масштабируемые сети сортировки, правила создания которых известны для произвольного числа процессоров, и немасштабируемые сети, предназначенные для выполнения только на вычислительных системах некоторых фиксированных размеров.
К первым следует отнести сеть сортировки простой вставкой, сеть нечетно-четной перестановки, сеть четно-нечетного слияния Бетчера и сеть битонной сортировки. Среди немасштабируемых известны оптимальных, с точки зрения времени выполнения сортировки, сетей для 6, 10 элементов[1], а так же наилучшие из известных сегодня сетей для 12 и 16 элементов.
1.2 Математическое описание алгоритма
Исходные данные: одномерный массив [math]A[/math], содержащий [math]n[/math] элементов, [math]|A|=n[/math].
Вычисляемые данные: упорядоченный массив [math]B=sort(A)[/math].
1.2.1 Постановка задачи
Сортировкой, или упорядочиванием элементов, называется процесс их расположения согласно определенному линейному отношению порядка, такому как отношение «меньше или равно» для чисел.
Если не оговорено иное, будем считать, что сортировка выполняется на вычислительной системе с распределенной памятью. Данное предположение, благодаря потенциальной возможности обработки произвольно большого набора данных, существенно расширяет область применимости рассматриваемых методов.
Без ограничения общности рассмотрим задачу расположения [math]n[/math] элементов массива в порядке неубывания. Пусть [math]B^i[/math] – [math]i[/math]-ый элемент массива [math]B[/math]. Тогда, массив [math]B[/math] упорядочен, если выполняется соотношение:
[math]B^i\le B^j[/math] , для любых допустимых [math]i,j[/math], при [math]i \lt j[/math].
Уточним, что будет пониматься под упорядоченным массивом в том случае, когда его части распределены по нескольким процессорам. Пусть элементы массива распределены по процессорам некоторыми порциями [math]B_i[/math], [math]B=\bigcup\limits_{i} B_i[/math].
Пусть [math]B_i^k[/math] – [math]k[/math]-ый элемент [math]i[/math]-го фрагмента массива [math]B[/math] (фрагмента, расположенного на процессоре [math]i[/math]).
Тогда, массив [math]B[/math] упорядочен, если выполняются следующие соотношения:
[math]B_i^k\le B_i^j[/math] , для любых [math]i[/math], при [math]k \lt j[/math],
[math]B_i^k\le B_l^j[/math] , для любых [math]k,j[/math], при [math]i \lt l[/math].
Пусть число используемых процессоров равно [math]p[/math]. Будем предполагать, что исходный массив [math]A[/math] распределен по процессорам некоторыми порциями [math]A_i[/math], где [math]0 \le i \le p-1[/math] – номер процессора, [math]A=\bigcup\limits_{i} A_i[/math]. Потребуем, чтобы размеры всех порций были одинаковы: [math]|A_i|=|A_j|, |A_i|=|B_i|[/math], для любых [math]i,j[/math]. Как будет показано ниже, только при выполнении этого условия, рассматриваемые параллельные алгоритмы, основанные на сетях сортировки, дают верный результат для любого исходного расположения элементов массива [math]A[/math]. В случае, если число элементов сортируемого массива не делится нацело на число процессоров, можно дополнить исходный массив фиктивными элементами, исключив их после окончания сортировки.
1.2.2 Временные материалы (в таком виде их не следует включать)
Можно указать три больших класса последовательных алгоритмов сортировки, отличающихся оценкой вычислительной сложности (видом зависимости числа выполняемых операций от размера массива). Алгоритмы сортировки, основанные на сравнении элементов, имеют сложность порядка [math]O(n^2)[/math] операций, где [math]n[/math] – число сортируемых элементов, что неприемлемо при больших значениях n, либо [math]O(n log_2(n))[/math] операций. Эти методы отличаются универсальностью. Последние из них взяты за основу «наилучшего» последовательного алгоритма сортировки. Известны методы поразрядной сортировки, обеспечивающие выполнение сортировки за [math]O(nk)[/math] операций, где [math]k[/math] – разрядность сортируемых данных, но их реализация существенно зависит от типа сортируемых данных, в связи с чем далее они не рассматриваются.
1.3 Вычислительное ядро алгоритма
Рассмотрим ряд сетей сортировки в предположении, что на каждой линии сети расположен ровно один элемент массива: [math]n = p[/math]:
сеть сортировки простой вставкой
сеть нечетно-четной перестановки
сеть четно-нечетного слияния Бетчера
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Кнут Д.Э. Искусство программирования. – Т.3. – Сортировка и поиск 2-е изд.: Пер. с английского – М.: Вильямс, 2001. – 824 с.
- Седжвик Роберт. Фундаментальные алгоритмы на С++. Анализ/Структуры данных/Сортировка/Поиск: Пер. с англ./Роберт Седжвик. - СПб.: ООО "ДиаСофтЮП", 2002.-688с.