Участник:RandomAtHome/Блочная cортировка: различия между версиями
(Скопирован шаблон описания алгоритма) |
(Доделана страница в вики для задания) |
||
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | Автор - студент 401 группы факультета ВМК Чухарев Фёдор Сергеевич. | |
| − | |||
| − | |||
Общая схема описания алгоритмов имеет следующий вид: | Общая схема описания алгоритмов имеет следующий вид: | ||
== Свойства и структура алгоритмов == | == Свойства и структура алгоритмов == | ||
| − | |||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | + | Блочная сортировка (Карманная сортировка, корзинная сортировка, англ. Bucket sort) — алгоритм сортировки, в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо любой другой сортировкой. Затем элементы помещаются обратно в массив. Данный алгоритм требует знаний о природе сортируемых данных, выходящих за рамки функций "сравнить" и "поменять местами", достаточных для большинства других сортировок - например сортировки слиянием, сортировки пирамидой, быстрой сортировки, сортировки Шелла, сортировки вставкой и т.д. В данном случае, дополнительные знания о данных нужны для того, чтобы правильно составить функцию распределяющую элементы по блокам, чтобы количество элементов в каждом блоке было примерно одинаковым. | |
| − | = | + | Особенностью блочной сортировки является то, что она может обладать линейным временем исполнения на удачных входных данных <ref name="ref1">Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клифорд. Глава 8. Сортировка за линейное время // Алгоритмы: построение и анализ, 2-е издание = Introduction to Algorithms second edition. — М.: «Вильямс», 2005. — С. 230 - 234</ref>, а также очень сильно деградировать на неудачных, в зависимости от алгоритма использующегося внутри блока сортировки. Например, в случае если блок сортируется с помощью сортировки вставками, то сложность становится равной <math>O(n^2)</math>. |
| − | |||
| − | = | + | Другим интересным примером является случай если число блоков <math>n = 2</math> и используется рекурсивная блочная сортировка - тогда алгоритм, по сути, становится эквивалентен сортировке Хоара. |
| − | |||
| − | + | Лучше всего алгоритм работает, когда для входных данных удается построить функцию, равномерно распределяющую их по блокам. Хороший пример - набор чисел с фиксированной точкой равномерно распределенный на отрезке <math>[0, 1)</math>. Иными словами, сортировка отлично подходит для случаев когда данные случайны и равномерно распределены по диапазону с известными границах. | |
| − | |||
| − | + | Еще стоит отметить, что в алгоритме в качестве внутренней сортировки часто используется сортировка вставками из-за некоторых ее свойств: | |
| − | + | * Сортировка вставками может работать по мере поступления данных, в отличие от той же сортировки Хоара или сортировки слиянием | |
| + | * Из-за константных множителей и членов более низкого порядка сортировка вставками может выполняться для небольших входных данных быстрее, чем другие сортировки с более низким порядком роста<ref>Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. 2.1. Сортировка вставкой // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 3-е изд. — М.: Вильямс, 2013. — С. 51.</ref> | ||
| + | |||
| + | === Математическое описание алгоритма === | ||
| + | Пусть у нас есть массив из <math>n</math> элементов распределенных равномерно в каком-то неизвестном нам диапазоне и <math>k</math> блоков, по которым мы распределяем эти элементы. | ||
| + | Оценим среднее время работы алгоритма блочной сортировки для случая, при котором в качестве алгоритма сортировки блоков используется сортировка вставками. | ||
| − | + | Первый шаг - проиницилизировать блоки, найдя наибольший и наименьший элементы. Это возможно сделать за <math>O(n)</math>, за один проход по массиву. Второй шаг, распределение элементов по блокам, вообще говоря, тоже занимает <math>O(n)</math> времени. Так как мы предположили, что внутренней сортировкой является сортировка вставками, то внутренняя сортировка займет <math>O(\textstyle \sum_{i=1}^k \displaystyle n_i^2)</math> времени, где <math>n_i</math> - размер блока с индексом <math>i</math>. | |
| − | + | Так как мы считаем среднее время, то надо вычислить математическое ожидание <math>E(n_i^2)</math>. | |
| − | + | Введем случайную величину <math>X_{ij}</math>, которая равна <big>1</big>, если <code>A[j]</code> попадает в ''i''-й карман, и <big>0</big> в противном случае. | |
| + | Очевидно, что <math>n_i = \sum_{j=1}^n X_{ij}</math>. Тогда, | ||
| − | + | :<math>\begin{align} | |
| + | E(n_i^2) & = E\left(\sum_{j=1}^n X_{ij} \sum_{k=1}^n X_{ik}\right) \\ | ||
| + | & = E\left(\sum_{j=1}^n \sum_{k=1}^n X_{ij}X_{ik}\right) \\ | ||
| + | & = E\left(\sum_{j=1}^n X_{ij}^2\right) + E\left(\sum_{1\leq j,k\leq n}\sum_{j\neq k}X_{ij}X_{ik}\right) | ||
| + | \end{align} </math> | ||
| − | = | + | В последней строчке сумма разделяется на случай <math>j=k</math> и случай <math>j\neq k</math>. Так как вероятность того, что элемент попадет в блок с индексом <math>i</math> равна <math>1/k</math>, <math>X_{ij} </math> равна 1 с вероятностью <math>1/k</math> и равна 0 иначе. |
| − | |||
| − | + | :<math>E(X_{ij}^2) = 1^2\cdot \left(\frac{1}{k}\right) + 0^2\cdot \left(1-\frac{1}{k}\right) = \frac{1}{k}</math> | |
| + | :<math>E(X_{ij}X_{ik}) = 1\cdot \left(\frac{1}{k}\right)\left(\frac{1}{k}\right) = \frac{1}{k^2} </math> | ||
| − | + | Подставим эти выражения в сумму и получим: | |
| − | == | + | :<math>E\left(\sum_{j=1}^n X_{ij}^2\right) + E\left(\sum_{1\leq j,k\leq n}\sum_{j\neq k}X_{ij}X_{ik}\right) = n\cdot\frac{1}{k} + n(n-1)\cdot\frac{1}{k^2} = \frac{n^2+nk-n}{k^2}</math> |
| − | |||
| − | + | Следовательно, вычислительная сложность алгоритма равна <math>O\left(\sum_{i=1}^kE(n_i^2)\right) = O\left(\sum_{i=1}^k \frac{n^2+nk-n}{k^2}\right) = O\left(\frac{n^2}{k}+n\right) </math>. | |
| − | + | Последний шаг алгоритма, объединение всех блоков в один массив занимает <math>O(k)</math> времени. Следовательно, общая сложность алгоритма равна <math>O\left(n+\frac{n^2}{k}+k\right)</math>. Если k выбрать как некоторую функцию от <math>n</math>, <math>k = \Theta(n)</math>, то вообще говоря среднее время будет равно <math>O(n)</math>, при условии что входные данные равномерно распределены. | |
| − | |||
| − | + | === Вычислительное ядро алгоритма === | |
| + | Вычислительное ядро, в данном случае, целиком совпадает с математическим описанием алгоритма. Большая часть работы уходит на внутренние сортировки в каждом блоке, при условии что общее время работы равно, по сути, самому худшему времени сортировки среди блоков, к которому прибавляется относительно стабильное время рассылки и сбора отсортированных данных. | ||
| − | + | === Макроструктура алгоритма === | |
| + | В качестве элементов макроструктуры в данном алгоритме можно указать внутренние сортировки в блоках. В них возможны вариации. Как было написано в общем описании алгоритма, существуют варианты когда в качестве внутренней сортировки используется не быстрый в среднем qsort или другие логарифмические сортировки, а сортировка вставками. Такое бывает, если число сортируемых данных мало или когда данные распределяются в режиме реального времени порциями. | ||
| − | + | === Схема реализации последовательного алгоритма === | |
| − | + | Опишем схему последовательного алгоритма. | |
| + | Пусть у нас есть N элементов, p массивов-блоков и заранее известная функция распределения f, которая определяет в какой блок надо отправить элемент. | ||
| − | + | 1) Подготовим p массивов, по которым мы будем распределять элементы | |
| − | |||
| − | + | 2) Пройдем по всем N элементам, распределяя их по блокам с помощью функции f | |
| − | + | 3) Пройдем последовательно по всем блокам, отсортировывая их некоторой внутренней сортировкой | |
| − | + | 4) Соединим все блоки назад в один массив | |
| − | + | Таким образом, мы последовательно отсортировали последовательность из N элементов, используя блочную сортировку. | |
| − | |||
| − | === | + | === Последовательная сложность алгоритма === |
| − | + | К сожалению последовательная сложность алгоритма может быть оценена только асимптотически, так как реальная сложность операций зависит от типа входных данных и от их распределения. При достаточно хорошем случае и правильно подобранном числе вычислительных блоков сложность может быть асимптотически равна <math>O(n)</math>, за счет малого числа элементов внутри блока для сортировки, однако есть шанс, что эта асимптотика деградирует асимптотики внутренней сортировки, например <math>O(n^2)</math> или <math>O(nlog(n))</math> - например в частном случае, если все элементы попали в один блок. | |
| − | + | === Информационный граф === | |
| + | За неимением изображения графа, ограничимся его словесным описанием. | ||
| − | + | Информационным графом здесь будет трехярусный граф, у которого на 1м ярусе и на 3м по одной вершине, вершина с 1ого яруса соединена со всеми вершинами со 2го, все вершины соединены с вершиной 3его. | |
| − | + | Вершина 1го яруса представляет собой последовательную часть с предобработкой и распределением данных, 2ой ярус это независимая сортировка блоков, 3ий ярус это сбор всех результатов сортировок блоков. | |
| − | + | Таким образом становится явно видно, что в алгоритме хорошо разделяется информация. | |
| − | + | === Ресурс параллелизма алгоритма === | |
| + | Как было видно из информационного графа, есть три этапа данного алгоритма - распределение данных, внутренние сортировки и сбор данных. Если первый и последний шаги требует все тех же N действий, то есть проход по всем исходным данным, то второй этап отлично параллелизуется - в предельном случае, если каждый блок будет соответствовать одному значению элемента, то само выполнение распределения по блокам будет являть собой, по сути, полную сортировку, так как массив из одинаковых элементов даже не нужно сортировать. Большую роль для параллелизма сортировок играет, опять же, полная независимость данных каждого из блоков. | ||
| − | + | === Входные и выходные данные алгоритма === | |
| + | Для эффективной работы алгоритма на входные данные накладывается существенные ограничения: | ||
| + | * Данные должны быть достаточно равномерно распределены по тому параметру, по которому производится сортировка | ||
| + | * На начало работы алгоритма должны быть известны верхняя и нижние границы, внутри которых находятся все сортируемые элементы | ||
| + | На самом деле второе условие за может быть достигнуто за дополнительный линейный проход по всем исходным данным, а несоблюдение первого приведет к ухудшению асимптотики и времени работы | ||
| + | алгоритма, вплоть до худшего случая когда практически все элементы находятся в одном блоке. | ||
| − | + | Результатом работы алгоритма является отсортированный набор данных. | |
| − | + | === Свойства алгоритма === | |
| + | Алгоритм содержит последовательную часть в самом начале, связанную с распределением данных. | ||
| − | + | Устойчивость алгоритма в смысле устойчивости сортировки зависит от устойчивости внутренней сортировки - при передаче данных их относительный порядок сохраняется. При этом алгоритм детерминирован. | |
| − | + | Вычислительную мощность можно оценить так - на передаваемый туда и обратно массив из N элементов приходится порядка <math>N*log(N)</math> операций, делаемых внутренней сортировкой. Так данные передаются назад в том же объеме, можно оценить что вычислительная мощность ~= <math>log(N)/2</math> в среднем. В зависимости от сортировки, если у нее асимптотика <math>O(N^2)</math>, то вычислительная мощность равна <math>N/2</math>. То есть, параллелизация может дать большой выигрыш по сравнению с последовательной версией. | |
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| − | |||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Локальность данных и вычислений === | === Локальность данных и вычислений === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
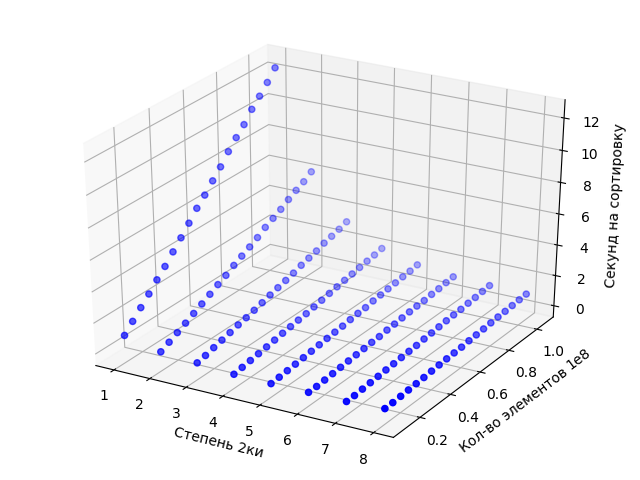
| − | + | На рис.1 продемонстрирована масштабируемость алгоритма, полученная опытным путем. Шкала по числу процессов логарифмирована, то есть реально использованное число процессов равно <math>2^s</math>. Стоит отметить, что с ростом числа процессов p время на сортировку уменьшается с асимптотикой <math>p^{-1}</math>, или же со скоростью <math>e^-s</math>, где <math>s = ln(p)</math>. Это явно видно на рис.2. Графики функции оценки ниже фактически получившихся значений времени, так как не учитывается overhead и затраты на пересылку и сбор данных, а лишь оценивается скорость падения времени. Зная асимптотику от числа процессов, легко оценить, с какого момента добавление новых процессов будет не столь эффективно. Так, по рис.2 видно что переход от 8 к 16 процессам (от 3ей степени к 4ой) и далее уже далеко не столь эффективны. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[File:Масштабируемость блочной сортировки.png|thumb|center|700px|Рис.1 Масштабируемость блочной сортировки]] | ||
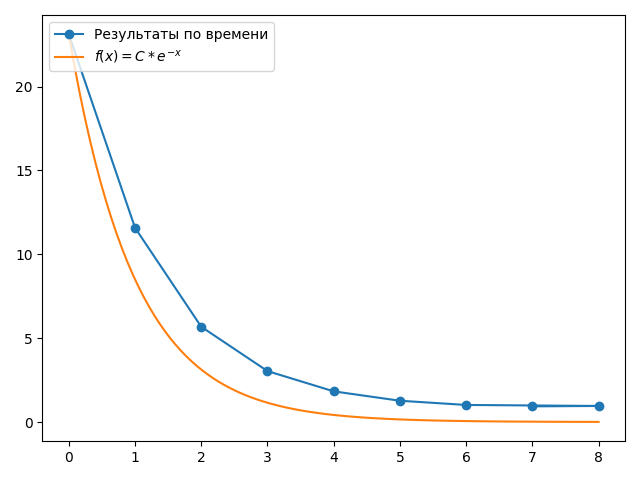
| + | [[File:Срез по числу элементов для блочной сортировки.png|thumb|center|700px|Рис.2 Cрез для числа элементов равного <math>10^{8}</math>]] | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
| − | |||
| − | |||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | |||
| − | |||
| − | |||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| − | + | Реализаций этого алгоритма и его подвидов не так много, так как они требуют дополнительной памяти и достаточно чувствительны к "хорошести" входных данных. | |
| + | Смешанную с блочной сортировкой реализацию имеет SpreadSort, использующийся в библиотеке Boost для C++. (https://www.boost.org/doc/libs/1_58_0/libs/sort/doc/html/index.html) | ||
| + | == Литература == | ||
| − | |||
<references /> | <references /> | ||
| − | |||
| − | |||
Текущая версия на 06:43, 4 декабря 2019
Автор - студент 401 группы факультета ВМК Чухарев Фёдор Сергеевич.
Общая схема описания алгоритмов имеет следующий вид:
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Блочная сортировка (Карманная сортировка, корзинная сортировка, англ. Bucket sort) — алгоритм сортировки, в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо любой другой сортировкой. Затем элементы помещаются обратно в массив. Данный алгоритм требует знаний о природе сортируемых данных, выходящих за рамки функций "сравнить" и "поменять местами", достаточных для большинства других сортировок - например сортировки слиянием, сортировки пирамидой, быстрой сортировки, сортировки Шелла, сортировки вставкой и т.д. В данном случае, дополнительные знания о данных нужны для того, чтобы правильно составить функцию распределяющую элементы по блокам, чтобы количество элементов в каждом блоке было примерно одинаковым.
Особенностью блочной сортировки является то, что она может обладать линейным временем исполнения на удачных входных данных [1], а также очень сильно деградировать на неудачных, в зависимости от алгоритма использующегося внутри блока сортировки. Например, в случае если блок сортируется с помощью сортировки вставками, то сложность становится равной O(n^2).
Другим интересным примером является случай если число блоков n = 2 и используется рекурсивная блочная сортировка - тогда алгоритм, по сути, становится эквивалентен сортировке Хоара.
Лучше всего алгоритм работает, когда для входных данных удается построить функцию, равномерно распределяющую их по блокам. Хороший пример - набор чисел с фиксированной точкой равномерно распределенный на отрезке [0, 1). Иными словами, сортировка отлично подходит для случаев когда данные случайны и равномерно распределены по диапазону с известными границах.
Еще стоит отметить, что в алгоритме в качестве внутренней сортировки часто используется сортировка вставками из-за некоторых ее свойств:
- Сортировка вставками может работать по мере поступления данных, в отличие от той же сортировки Хоара или сортировки слиянием
- Из-за константных множителей и членов более низкого порядка сортировка вставками может выполняться для небольших входных данных быстрее, чем другие сортировки с более низким порядком роста[2]
1.2 Математическое описание алгоритма
Пусть у нас есть массив из n элементов распределенных равномерно в каком-то неизвестном нам диапазоне и k блоков, по которым мы распределяем эти элементы. Оценим среднее время работы алгоритма блочной сортировки для случая, при котором в качестве алгоритма сортировки блоков используется сортировка вставками.
Первый шаг - проиницилизировать блоки, найдя наибольший и наименьший элементы. Это возможно сделать за O(n), за один проход по массиву. Второй шаг, распределение элементов по блокам, вообще говоря, тоже занимает O(n) времени. Так как мы предположили, что внутренней сортировкой является сортировка вставками, то внутренняя сортировка займет O(\textstyle \sum_{i=1}^k \displaystyle n_i^2) времени, где n_i - размер блока с индексом i. Так как мы считаем среднее время, то надо вычислить математическое ожидание E(n_i^2).
Введем случайную величину X_{ij}, которая равна 1, если A[j] попадает в i-й карман, и 0 в противном случае.
Очевидно, что n_i = \sum_{j=1}^n X_{ij}. Тогда,
- \begin{align} E(n_i^2) & = E\left(\sum_{j=1}^n X_{ij} \sum_{k=1}^n X_{ik}\right) \\ & = E\left(\sum_{j=1}^n \sum_{k=1}^n X_{ij}X_{ik}\right) \\ & = E\left(\sum_{j=1}^n X_{ij}^2\right) + E\left(\sum_{1\leq j,k\leq n}\sum_{j\neq k}X_{ij}X_{ik}\right) \end{align}
В последней строчке сумма разделяется на случай j=k и случай j\neq k. Так как вероятность того, что элемент попадет в блок с индексом i равна 1/k, X_{ij} равна 1 с вероятностью 1/k и равна 0 иначе.
- E(X_{ij}^2) = 1^2\cdot \left(\frac{1}{k}\right) + 0^2\cdot \left(1-\frac{1}{k}\right) = \frac{1}{k}
- E(X_{ij}X_{ik}) = 1\cdot \left(\frac{1}{k}\right)\left(\frac{1}{k}\right) = \frac{1}{k^2}
Подставим эти выражения в сумму и получим:
- E\left(\sum_{j=1}^n X_{ij}^2\right) + E\left(\sum_{1\leq j,k\leq n}\sum_{j\neq k}X_{ij}X_{ik}\right) = n\cdot\frac{1}{k} + n(n-1)\cdot\frac{1}{k^2} = \frac{n^2+nk-n}{k^2}
Следовательно, вычислительная сложность алгоритма равна O\left(\sum_{i=1}^kE(n_i^2)\right) = O\left(\sum_{i=1}^k \frac{n^2+nk-n}{k^2}\right) = O\left(\frac{n^2}{k}+n\right) .
Последний шаг алгоритма, объединение всех блоков в один массив занимает O(k) времени. Следовательно, общая сложность алгоритма равна O\left(n+\frac{n^2}{k}+k\right). Если k выбрать как некоторую функцию от n, k = \Theta(n), то вообще говоря среднее время будет равно O(n), при условии что входные данные равномерно распределены.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро, в данном случае, целиком совпадает с математическим описанием алгоритма. Большая часть работы уходит на внутренние сортировки в каждом блоке, при условии что общее время работы равно, по сути, самому худшему времени сортировки среди блоков, к которому прибавляется относительно стабильное время рассылки и сбора отсортированных данных.
1.4 Макроструктура алгоритма
В качестве элементов макроструктуры в данном алгоритме можно указать внутренние сортировки в блоках. В них возможны вариации. Как было написано в общем описании алгоритма, существуют варианты когда в качестве внутренней сортировки используется не быстрый в среднем qsort или другие логарифмические сортировки, а сортировка вставками. Такое бывает, если число сортируемых данных мало или когда данные распределяются в режиме реального времени порциями.
1.5 Схема реализации последовательного алгоритма
Опишем схему последовательного алгоритма. Пусть у нас есть N элементов, p массивов-блоков и заранее известная функция распределения f, которая определяет в какой блок надо отправить элемент.
1) Подготовим p массивов, по которым мы будем распределять элементы
2) Пройдем по всем N элементам, распределяя их по блокам с помощью функции f
3) Пройдем последовательно по всем блокам, отсортировывая их некоторой внутренней сортировкой
4) Соединим все блоки назад в один массив
Таким образом, мы последовательно отсортировали последовательность из N элементов, используя блочную сортировку.
1.6 Последовательная сложность алгоритма
К сожалению последовательная сложность алгоритма может быть оценена только асимптотически, так как реальная сложность операций зависит от типа входных данных и от их распределения. При достаточно хорошем случае и правильно подобранном числе вычислительных блоков сложность может быть асимптотически равна O(n), за счет малого числа элементов внутри блока для сортировки, однако есть шанс, что эта асимптотика деградирует асимптотики внутренней сортировки, например O(n^2) или O(nlog(n)) - например в частном случае, если все элементы попали в один блок.
1.7 Информационный граф
За неимением изображения графа, ограничимся его словесным описанием.
Информационным графом здесь будет трехярусный граф, у которого на 1м ярусе и на 3м по одной вершине, вершина с 1ого яруса соединена со всеми вершинами со 2го, все вершины соединены с вершиной 3его.
Вершина 1го яруса представляет собой последовательную часть с предобработкой и распределением данных, 2ой ярус это независимая сортировка блоков, 3ий ярус это сбор всех результатов сортировок блоков.
Таким образом становится явно видно, что в алгоритме хорошо разделяется информация.
1.8 Ресурс параллелизма алгоритма
Как было видно из информационного графа, есть три этапа данного алгоритма - распределение данных, внутренние сортировки и сбор данных. Если первый и последний шаги требует все тех же N действий, то есть проход по всем исходным данным, то второй этап отлично параллелизуется - в предельном случае, если каждый блок будет соответствовать одному значению элемента, то само выполнение распределения по блокам будет являть собой, по сути, полную сортировку, так как массив из одинаковых элементов даже не нужно сортировать. Большую роль для параллелизма сортировок играет, опять же, полная независимость данных каждого из блоков.
1.9 Входные и выходные данные алгоритма
Для эффективной работы алгоритма на входные данные накладывается существенные ограничения:
- Данные должны быть достаточно равномерно распределены по тому параметру, по которому производится сортировка
- На начало работы алгоритма должны быть известны верхняя и нижние границы, внутри которых находятся все сортируемые элементы
На самом деле второе условие за может быть достигнуто за дополнительный линейный проход по всем исходным данным, а несоблюдение первого приведет к ухудшению асимптотики и времени работы алгоритма, вплоть до худшего случая когда практически все элементы находятся в одном блоке.
Результатом работы алгоритма является отсортированный набор данных.
1.10 Свойства алгоритма
Алгоритм содержит последовательную часть в самом начале, связанную с распределением данных.
Устойчивость алгоритма в смысле устойчивости сортировки зависит от устойчивости внутренней сортировки - при передаче данных их относительный порядок сохраняется. При этом алгоритм детерминирован.
Вычислительную мощность можно оценить так - на передаваемый туда и обратно массив из N элементов приходится порядка N*log(N) операций, делаемых внутренней сортировкой. Так данные передаются назад в том же объеме, можно оценить что вычислительная мощность ~= log(N)/2 в среднем. В зависимости от сортировки, если у нее асимптотика O(N^2), то вычислительная мощность равна N/2. То есть, параллелизация может дать большой выигрыш по сравнению с последовательной версией.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
На рис.1 продемонстрирована масштабируемость алгоритма, полученная опытным путем. Шкала по числу процессов логарифмирована, то есть реально использованное число процессов равно 2^s. Стоит отметить, что с ростом числа процессов p время на сортировку уменьшается с асимптотикой p^{-1}, или же со скоростью e^-s, где s = ln(p). Это явно видно на рис.2. Графики функции оценки ниже фактически получившихся значений времени, так как не учитывается overhead и затраты на пересылку и сбор данных, а лишь оценивается скорость падения времени. Зная асимптотику от числа процессов, легко оценить, с какого момента добавление новых процессов будет не столь эффективно. Так, по рис.2 видно что переход от 8 к 16 процессам (от 3ей степени к 4ой) и далее уже далеко не столь эффективны.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Реализаций этого алгоритма и его подвидов не так много, так как они требуют дополнительной памяти и достаточно чувствительны к "хорошести" входных данных. Смешанную с блочной сортировкой реализацию имеет SpreadSort, использующийся в библиотеке Boost для C++. (https://www.boost.org/doc/libs/1_58_0/libs/sort/doc/html/index.html)
3 Литература
- ↑ Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клифорд. Глава 8. Сортировка за линейное время // Алгоритмы: построение и анализ, 2-е издание = Introduction to Algorithms second edition. — М.: «Вильямс», 2005. — С. 230 - 234
- ↑ Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. 2.1. Сортировка вставкой // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 3-е изд. — М.: Вильямс, 2013. — С. 51.