Участник:One/Алгоритм распределения булевых функций на гиперсфере: различия между версиями
One (обсуждение | вклад) |
One (обсуждение | вклад) |
||
| (не показано 18 промежуточных версий этого же участника) | |||
| Строка 18: | Строка 18: | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| + | Вычислительным ядром данного алгоритма является перебор всех возможных функций от заданного количества переменных, так как количество таких функций равно [math]2^{2^n}[/math]. Функции можно отождествить с их вектором значений, который в свою очередь можно перевести в число из двоичной системы в десятичную. Таким образом, генерация или перебор всех возможных булевых функций от [math]n[/math] переменных сводится к перебору всех возможных чисел в диапазоне от [math]0[/math] до [math]2^{2^n}[/math], не включая последнее значение. | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| + | Распределение функций на гиперсферу Евклидового пространства производится несколько этапов: | ||
| + | # Генерация и перебор всех возможных булевых функций от заданного числа переменных. | ||
| + | # Вычисление спектра Уолша для каждой функции по указанной ранее формуле. | ||
| + | # На основе спектра Уолша создание вектора значений функции-номера секции. | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| + | В данном разделе представлена схема реализации последовательного алгоритма на языке Python. | ||
| + | |||
| + | '''1 этап''' Прямой перебор по порядку чисел в диапазоне [math][0, 2^{2^n}][/math]. | ||
| + | |||
| + | '''2 этап''' Перевод числа в вектор значений функции: | ||
| + | vv = bin(value) | ||
| + | vv = vv[2:] | ||
| + | vv = vv.rjust(2**n, '0') | ||
| + | |||
| + | '''3 этап''' Вычисление спектра Уолша (ws): (на данном этапе [math]scalar(x, y, n)[/math] - скалярное произведение векторов [math]x[/math] и [math]y[/math] в пространстве [math]V_n[/math]) | ||
| + | ws = [0] * (2**n) | ||
| + | for u in range(0, 2**n): | ||
| + | res = 0 | ||
| + | for x in range(0, 2**n): | ||
| + | power = 0 | ||
| + | power += scalar(x, u, n) | ||
| + | power += int(vv[x]) | ||
| + | power %= 2 | ||
| + | if power == 0: | ||
| + | res += 1 | ||
| + | else: | ||
| + | res += (-1) | ||
| + | ws[u] = res | ||
| + | |||
| + | '''4 этап''' Вычисление вектора значений функции-номера секции на основе спектра Уолша: | ||
| + | section_number = [0] * (2**n) | ||
| + | for index in range(0, 2**n): | ||
| + | if ws[index] > 0: | ||
| + | section_number[index] = 0 | ||
| + | if ws[index] < 0: | ||
| + | section_number[index] = 1 | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | Обозначим через [math]w[/math] значение, равное [math]2^n[/math]. | ||
| + | |||
| + | Тогда сложность вычисления коэффициента Уолша для определенной функции: [math]w[/math] вычислений скалярного произведения, затем суммирование полученных величин -> сложность: [math]w-1[/math]. Т.е. общая сложность равна [math]2w-1[/math]. | ||
| + | |||
| + | Следовательно вычисление спектра Уолша зафиксированной функции имеет сложность: [math]w*(2w-1) = 2w^2-w[/math]. | ||
| + | |||
| + | Всего нужно вычислить спектр Уолша для каждой функции, т.е. [math](2w^2-w)*2^w = O(w^2 * 2^w)[/math]. | ||
| + | |||
| + | А генерация вектора значения функции-номера секции просто генерируется на основе значений спектра Уолша. Таким образом, общая сложность последовательной реализации алгоритма составляет [math]O(2^{2^n}*2^{2n})[/math] | ||
=== Информационный граф === | === Информационный граф === | ||
| + | Так как весь алгоритм 'сосредоточен' в главном цикле перебора всех возможных чисел, то именно для этого фрагмента реализации алгоритма построим информационный граф. | ||
| + | |||
| + | Подграф желаемого графа указан на рисунке 1, где: | ||
| + | |||
| + | [VV] - преобразование числа в вектор значение булевой функции, т.е. фактически перевод десятичного числа в двоичную систему счисления. | ||
| + | |||
| + | [WS] - нахождение спектра Уолша на основе вектора значений. | ||
| + | |||
| + | [F-N S] - генерация вектора значений функции-номера секции на основе спектра Уолша. | ||
| + | |||
| + | [[file:BoolFunc_IG.png|thumb|center|500px|Рисунок 1. Подграф информационного графа алгоритма распределения булевых функций на гиперсфере.]] | ||
| + | |||
| + | Действительно, очевидно, что данный подграф отображает лишь одну итерацию всего цикла, т.е. весь информационный граф этого цикла будет состоять из [math]2^{2^n}[/math] одинаковых несвязных подграфов вида как на рисунке 1. | ||
| + | Из вида информационного графа сразу понятен ресурс параллелизма данного алгоритма - блочное (или циклическое) распределение итерация цикла между процессорами. | ||
| + | |||
| + | Обоснование, почему операцию нахождения спектра Уолша можно считать за работу оператора: в данной реализации алгоритма вычисление спектра Уолша производилось прямо по определению, однако в теории криптографии существует быстрое преобразование Адамара. Оно заключается в том, что существуют [https://ru.wikipedia.org/wiki/Матрица_Адамара матрицы Адамара] специального вида, обозначаемые [math]H_{2^n}[/math], которые используются для вычисления спектра Уолша по формуле: [math]WS = (-1)^f * H_{2^n}[/math], где [math](-1)^f[/math] - вектор вида [math]((-1)^{f(0)}, ..., (-1)^{f(1^n)})[/math]. | ||
=== Ресурс параллелелизма алгоритма === | === Ресурс параллелелизма алгоритма === | ||
| + | При параллелизации алгоритма был использован лишь одни доступный для этого ресурс - цикл перебора, использующийся для генерации векторов значений булевых функций. А именно - был использован блочный метод распределения итераций цикла. | ||
| + | То есть, был задан параметр, равный количеству доступных процессоров на используемой машине. На основе этого значения вычисляется размер 'порции' данных для каждого процессора по формуле: | ||
| + | portion = 2**(2**n) / num_procs | ||
| + | |||
| + | И каждый процессор в итоге обрабатывает лишь часть данных, которая вычисляется на основании номера процессора в коммуникаторе. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| + | |||
| + | '''Входные данные:''' Количество переменных, от которых зависят булевы функции. Предпочтительно задавать нечетные значения, значения [math]\ge 3[/math], но [math]\le 11[/math]. (т.к. именно для значений [math]n \le 11[/math] существуют [https://dspace.spbu.ru/bitstream/11701/4477/1/VKR_Anoxin_I_A_.pdf оценки максимальной нелинейности булевой функции.] , которые можно использовать для хотя бы частичной проверки корректности работы алгоритма) | ||
| + | |||
| + | '''Выходные данные:''' Словарь (в понятии языка Python), где ключу будет соответствовать вектор значений функции-номера секции, а значению соответствует количество функций в данной секции. | ||
| + | |||
| + | === Свойства алгоритма === | ||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| Строка 40: | Строка 112: | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | |||
| + | Для наглядной масштабируемости алгоритма представлен график (Рисунок 2) зависимости времени выполнения от количества переменных в булевой функции и от количества используемых процессоров. | ||
| + | |||
| + | [[file:BoolFunc_Chart.jpg|thumb|center|700px|Рисунок 2. График зависимости времени от количества входных переменных и степени распараллеливания.]] | ||
| + | |||
| + | |||
| + | Наглядно видно, что время при увеличении количества переменных увеличивается экспоненциально. Однако увеличение количества используемых процессоров немного улучшает ситуацию. Тем не менее, нельзя просто при любом количестве переменных брать максимально доступное число процессоров, ибо как видно при [math]n = 3[/math] такой выбор лишь усугубляет ситуацию - очень много времени уходит на сбор информации со всех процессоров, что в несколько раз увеличивает время работы алгоритма. Однако при увеличении [math]n[/math] увеличение количества используемых процессоров немного улучшает ситуацию со временем, но это далеко не панацея. | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
| Строка 46: | Строка 125: | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| − | + | В открытом доступе не было найдено реализаций данного алгоритма. | |
== Литература == | == Литература == | ||
Текущая версия на 10:27, 4 декабря 2020
Автор - Бартель Артем.
Одним из самых интересных свойств булевых функций, часто используемых в криптографии, является нелинейность. Для булевых функций, зависящих от четного количества переменных существует точная формула для подсчета нелинейности, а вот с функциями, зависящими от нечетного числа переменных такой формулы нет. Конечно же, существует общая формула вычисления нелинейности, но при достаточно больших [math]n[/math] (количество переменных) ей практически невозможно пользоваться, так как она подразумевает перебор всех возможных векторов длины [math]n[/math]. Именно поэтому хочется попытаться расширить используемый математический аппарат, чтобы получить более удобное решение поставленной проблемы. В данной статье будет рассматриваться метод распределения булевых функций на гиперсфере. На основе этого метода будут предприняты попытки нахождения закономерностей и связей между степенью нелинейности булевой функции и ее расположением на гиперсфере в евклидовом пространстве.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Объекты, с которыми работает данный алгоритм - булевы функции. Фактически, при задании [math]n[/math] - количество переменных, от которых зависит функция - будет выполнен полный перебор всех возможных векторов длины [math]2^{n}[/math] (это вектора, которые соответствуют значениям, которые функция принимает на всевозможных лексико-графически упорядоченных наборах длины [math]n[/math]), количество коих равно [math]2^{2^{n}}[/math]. Для каждого такого вектора будет подсчитана нужная характеристика - спектр Уолша, на основе которой будет составляться вектор так называемой функции-сектора, которая отвечает за то, в каком секторе гиперсферы находится исследуемая функция. На основе полученного распределения булевых функций на гиперсфере будут предприняты попытки нахождения зависимостей между функцией-сектором данной булевой функции и ее показателем нелинейности. Конечно же, особое внимание уделяется функциям, зависящим от нечетного числа переменных.
1.2 Математическое описание алгоритма
Через [math]V_{n}[/math] обозначим множество всевозможных двоичных векторов длины [math]n[/math]. Тогда отображение [math]f: V_{n} → V_{n}[/math] - булева функция. Коэффициентом Уолша заданной функции на векторе [math]u[/math] называется величина [math]W_{f}(u)[/math], определяемая формулой:
где [math]\lt u,x\gt [/math] - скалярное произведение соответствующих векторов: [math]\lt u,x\gt = Σ_{i=1}^{n}x_{i}u_{i}[/math], где [math]Σ[/math] - сложение по модулю 2. Соответственно спектром Уолша данной функции называется вектор вида [math](W_{f}(0^{n}), ..., W_{f}(1^{n}))[/math].
На основе данного вектора составляется вектор значений функции-сектора [math]g(x)[/math] по правилу:
Таким образом, мы получаем вектор значений функции, которая 'нумерует' определенную секцию гиперсферы. Легко видеть, что для булевых функций, у которых существует хотя бы один нулевой коэффициент Уолша, невозможно точно и однозначно определить секцию, в которой они лежат, то есть они находятся на стыке двух секторов. В дальнейшем будут исследоваться свойства полученных функций-секторов и их взаимосвязь с исходными булевыми функциями.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром данного алгоритма является перебор всех возможных функций от заданного количества переменных, так как количество таких функций равно [math]2^{2^n}[/math]. Функции можно отождествить с их вектором значений, который в свою очередь можно перевести в число из двоичной системы в десятичную. Таким образом, генерация или перебор всех возможных булевых функций от [math]n[/math] переменных сводится к перебору всех возможных чисел в диапазоне от [math]0[/math] до [math]2^{2^n}[/math], не включая последнее значение.
1.4 Макроструктура алгоритма
Распределение функций на гиперсферу Евклидового пространства производится несколько этапов:
- Генерация и перебор всех возможных булевых функций от заданного числа переменных.
- Вычисление спектра Уолша для каждой функции по указанной ранее формуле.
- На основе спектра Уолша создание вектора значений функции-номера секции.
1.5 Схема реализации последовательного алгоритма
В данном разделе представлена схема реализации последовательного алгоритма на языке Python.
1 этап Прямой перебор по порядку чисел в диапазоне [math][0, 2^{2^n}][/math].
2 этап Перевод числа в вектор значений функции:
vv = bin(value) vv = vv[2:] vv = vv.rjust(2**n, '0')
3 этап Вычисление спектра Уолша (ws): (на данном этапе [math]scalar(x, y, n)[/math] - скалярное произведение векторов [math]x[/math] и [math]y[/math] в пространстве [math]V_n[/math])
ws = [0] * (2**n)
for u in range(0, 2**n):
res = 0
for x in range(0, 2**n):
power = 0
power += scalar(x, u, n)
power += int(vv[x])
power %= 2
if power == 0:
res += 1
else:
res += (-1)
ws[u] = res
4 этап Вычисление вектора значений функции-номера секции на основе спектра Уолша:
section_number = [0] * (2**n)
for index in range(0, 2**n):
if ws[index] > 0:
section_number[index] = 0
if ws[index] < 0:
section_number[index] = 1
1.6 Последовательная сложность алгоритма
Обозначим через [math]w[/math] значение, равное [math]2^n[/math].
Тогда сложность вычисления коэффициента Уолша для определенной функции: [math]w[/math] вычислений скалярного произведения, затем суммирование полученных величин -> сложность: [math]w-1[/math]. Т.е. общая сложность равна [math]2w-1[/math].
Следовательно вычисление спектра Уолша зафиксированной функции имеет сложность: [math]w*(2w-1) = 2w^2-w[/math].
Всего нужно вычислить спектр Уолша для каждой функции, т.е. [math](2w^2-w)*2^w = O(w^2 * 2^w)[/math].
А генерация вектора значения функции-номера секции просто генерируется на основе значений спектра Уолша. Таким образом, общая сложность последовательной реализации алгоритма составляет [math]O(2^{2^n}*2^{2n})[/math]
1.7 Информационный граф
Так как весь алгоритм 'сосредоточен' в главном цикле перебора всех возможных чисел, то именно для этого фрагмента реализации алгоритма построим информационный граф.
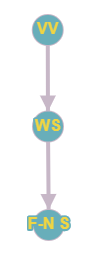
Подграф желаемого графа указан на рисунке 1, где:
[VV] - преобразование числа в вектор значение булевой функции, т.е. фактически перевод десятичного числа в двоичную систему счисления.
[WS] - нахождение спектра Уолша на основе вектора значений.
[F-N S] - генерация вектора значений функции-номера секции на основе спектра Уолша.
Действительно, очевидно, что данный подграф отображает лишь одну итерацию всего цикла, т.е. весь информационный граф этого цикла будет состоять из [math]2^{2^n}[/math] одинаковых несвязных подграфов вида как на рисунке 1. Из вида информационного графа сразу понятен ресурс параллелизма данного алгоритма - блочное (или циклическое) распределение итерация цикла между процессорами.
Обоснование, почему операцию нахождения спектра Уолша можно считать за работу оператора: в данной реализации алгоритма вычисление спектра Уолша производилось прямо по определению, однако в теории криптографии существует быстрое преобразование Адамара. Оно заключается в том, что существуют матрицы Адамара специального вида, обозначаемые [math]H_{2^n}[/math], которые используются для вычисления спектра Уолша по формуле: [math]WS = (-1)^f * H_{2^n}[/math], где [math](-1)^f[/math] - вектор вида [math]((-1)^{f(0)}, ..., (-1)^{f(1^n)})[/math].
1.8 Ресурс параллелелизма алгоритма
При параллелизации алгоритма был использован лишь одни доступный для этого ресурс - цикл перебора, использующийся для генерации векторов значений булевых функций. А именно - был использован блочный метод распределения итераций цикла. То есть, был задан параметр, равный количеству доступных процессоров на используемой машине. На основе этого значения вычисляется размер 'порции' данных для каждого процессора по формуле:
portion = 2**(2**n) / num_procs
И каждый процессор в итоге обрабатывает лишь часть данных, которая вычисляется на основании номера процессора в коммуникаторе.
1.9 Входные и выходные данные алгоритма
Входные данные: Количество переменных, от которых зависят булевы функции. Предпочтительно задавать нечетные значения, значения [math]\ge 3[/math], но [math]\le 11[/math]. (т.к. именно для значений [math]n \le 11[/math] существуют оценки максимальной нелинейности булевой функции. , которые можно использовать для хотя бы частичной проверки корректности работы алгоритма)
Выходные данные: Словарь (в понятии языка Python), где ключу будет соответствовать вектор значений функции-номера секции, а значению соответствует количество функций в данной секции.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
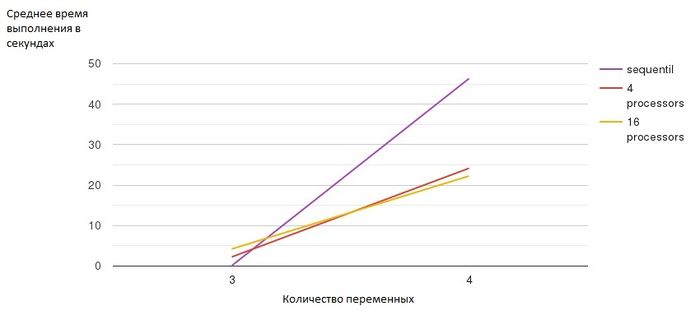
Для наглядной масштабируемости алгоритма представлен график (Рисунок 2) зависимости времени выполнения от количества переменных в булевой функции и от количества используемых процессоров.
Наглядно видно, что время при увеличении количества переменных увеличивается экспоненциально. Однако увеличение количества используемых процессоров немного улучшает ситуацию. Тем не менее, нельзя просто при любом количестве переменных брать максимально доступное число процессоров, ибо как видно при [math]n = 3[/math] такой выбор лишь усугубляет ситуацию - очень много времени уходит на сбор информации со всех процессоров, что в несколько раз увеличивает время работы алгоритма. Однако при увеличении [math]n[/math] увеличение количества используемых процессоров немного улучшает ситуацию со временем, но это далеко не панацея.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В открытом доступе не было найдено реализаций данного алгоритма.
3 Литература
- ↑ О.А. Логачев, С.Н. Федоров, В.В. Ященко. Булевы функции как точки гиперсферы в евклидовом пространстве // Общероссийский математический портал Math-Net.ru. 2018, том 30, выпуск 1, стр. 39-55
- ↑ О.А. Логачев, А.А. Сальников, С.В. Смышляев, В.В. Ященко. Булевы функции в теории кодирования и криптологии. 2012.
- ↑ Tomas Cusick, Pantelimon Stanica. Cryptographic Boolean Functions and Applications. 2009.