Дифференацильная атака: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Demiandr (обсуждение | вклад) |
Demiandr (обсуждение | вклад) |
||
| Строка 67: | Строка 67: | ||
=== Информационный граф === | === Информационный граф === | ||
| − | + | Рассмотрим [[глоссарий#Граф алгоритма|граф алгоритма]] для обработки одного текста как аналитически, так и в виде рисунка. | |
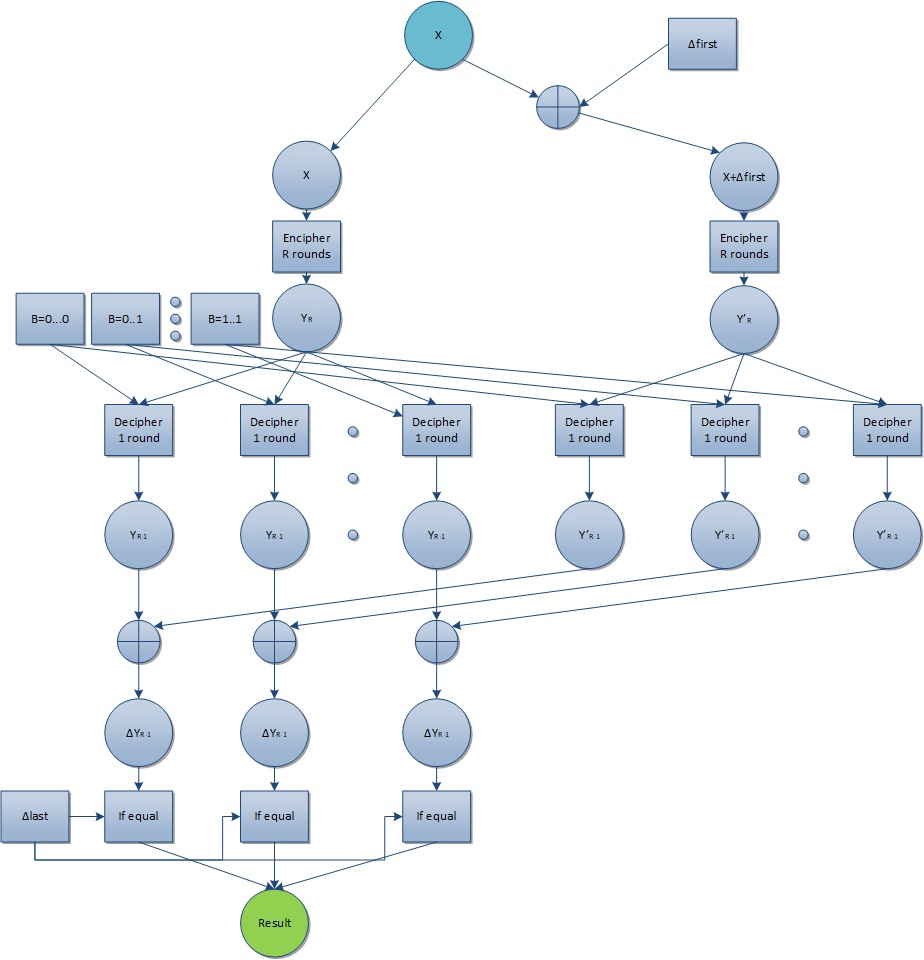
| − | [[Файл: | + | [[Файл:Graphdifferential.jpg|обрамить|центр|Информационная схема работы алгоритма]] |
| − | |||
| − | + | Как видно из рисунка, для каждого текста <math>X</math> сначала генерируется второй текст при помощи добавления к нему разницы <math>Δfirst</math>, взятой из дифференциальной характеристики, после чего происходит шифрование на протяжение <math>R</math> раундов для обеих текстов из пары. После получения шифртекстов <math>Y_R</math> и <math>Y'_R</math> в результате последнего раунда, для всех возможных <math>b</math> бит последнего раундового ключа происходит частичное расшифрование, после чего в каждой паре тексты складываются и их разница <math>ΔY_{R-1}</math> сравнивается с искомой <math>Δlast</math> в характеристике. Если разницы текстов совпадают, данные значения бит раундового ключа заносятся в результат. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
Версия 15:13, 4 ноября 2021
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Дифференциальный криптоанализ — метод криптоанализа симметричных блочных шифров (и других криптографических примитивов, в частности, хеш-функций и поточных шифров). Дифференциальный криптоанализ основан на изучении преобразования разностей между шифруемыми значениями на различных раундах шифрования. В качестве разности, как правило, применяется операция побитового суммирования по модулю 2, хотя существуют атаки и с вычислением разности по модулю {\displaystyle 2^{32}}2^{32}. Является статистической атакой. Применим для взлома DES, FEAL и некоторых других шифров, как правило, разработанных ранее начала 90-х. Количество раундов современных шифров (AES, Camellia и др.) рассчитывалось с учётом обеспечения стойкости, в том числе и к дифференциальному криптоанализу. Все существующие блочные алгоритмы шифрования являются итеративными алгоритмами, то есть при шифровании информация подвергается большому числу одних и тех же подряд идущих преобразований (раундов). В начале алгоритма шифрования из одного длинного секретного ключа при помощи алгоритма генерации раундовых ключей создаются мини-ключи, которые применяются на каждом раунде шифрования. Дифференциальный криптоанализ направлен на нахождение таких раундовых ключей, для последующего определения по ним основного секретного ключа криптосистемы, причем первым определяемым раундовым ключом является ключ последнего раунда шифрования.
1.2 Математическое описание алгоритма
Пусть [math]ΔX=({ΔX_1}{ΔX_2}{ΔX_3}...{ΔX_3})[/math] Задачей криптоаналитика является нахождение Пусть [math]{p}[/math] - вероя
1.3 Вычислительное ядро алгоритма
Вычислительное ядром алгоритма является генерация и шифрование большого числа входных пар текстов алгоритма шифрования с заданной разницей [math]ΔX[/math], получая в итоге пары шифртекстов. После генерации текстов для каждой комбинации пары шифртекстов и возможного значения бит раундового ключа последнего раунда найденной характеристики происходит частичное расшифрование шифртекстов. Если разница между парами текстов [math]ΔY_{R-1}[/math] на [math]{R-1}[/math] раунде совпадает с искомой разницей [math]ΔU[/math], счетчик данного значения бит раундового ключа последнего раунда инкрементируется. Результатом является значение раундового ключа с наибольшим счетчиком.
1.4 Макроструктура алгоритма
Как уже определено в описании ядра алгоритма, основную часть сложность алгоритма составляет большое количество операций шифрования определенных значений текстов.
1.5 Схема реализации последовательного алгоритма
В данном пункте приведены
double p = 0.000001;//вероятность найденной характеристики
int c = 2;//константа
int R = 12;//число раундов шифра
int b = 4;//число бит раундового ключа, которые можно определить найденной характеристикой
__uint64 deltafirst=(2^34);// найденная характеристика (разница между парой текстов)
__uint64 deltalast=1;(найденная разница между текстами на предпоследнем раунде_
__uint64 firsttext;//первый текст из пары
__uint64 secondtext;//второй текст из пары
int result[pow(2,b)]={};//массив возможных значений бит раундового ключа
for (__uint64 i=0; i<(c/p);i++)
{
firsttext=i;//генерация первого текста пары
secondtext=i^deltafirst;//генерация второго текста пары
for (int j=0; j<R;j++)
{
firsttext = cipher(firsttext);
secondtext = cipher(secondtext);
}
for (int k=0; k< pow(2,b);k++)
{
firsttext = decipher(firsttext,k)
secondtext = decipher(secondtext,k)
if (deltalast == firsttext ^ secondtext)
{
result[k]++
}
}
}
int max=0
for (int k=0; k< pow(2,b);k++)
{
if (result[k] > max) max=result[k]
}
1.6 Последовательная сложность алгоритма
Cчитая базовой операцией операцию шифрования текста на одном раунде с использование дифференциальной характеристики с вероятностью [math]p[/math], на нахождение [math]b[/math] бит раундового ключа [math]R-1[/math] раунда шифрования потребуется около [math](2c/p)(R+2^b)[/math] операций шифрования, где [math]с[/math] - некоторая небольшая константа. Так как основным параметром является вероятность [math]p[/math], от которой зависит числе пар текстов, данный алгоритм имеет линейную сложность.
1.7 Информационный граф
Рассмотрим граф алгоритма для обработки одного текста как аналитически, так и в виде рисунка.
Как видно из рисунка, для каждого текста [math]X[/math] сначала генерируется второй текст при помощи добавления к нему разницы [math]Δfirst[/math], взятой из дифференциальной характеристики, после чего происходит шифрование на протяжение [math]R[/math] раундов для обеих текстов из пары. После получения шифртекстов [math]Y_R[/math] и [math]Y'_R[/math] в результате последнего раунда, для всех возможных [math]b[/math] бит последнего раундового ключа происходит частичное расшифрование, после чего в каждой паре тексты складываются и их разница [math]ΔY_{R-1}[/math] сравнивается с искомой [math]Δlast[/math] в характеристике. Если разницы текстов совпадают, данные значения бит раундового ключа заносятся в результат.
1.8 Ресурс параллелизма алгоритма
Для алгоритма умножения квадратной матрицы на вектор порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы:
- по [math]n[/math] ярусов умножений и сложений (в каждом из ярусов — [math]n[/math] операций).
Для умножения матрицы размером [math]m[/math] строк на [math]n[/math] столбцов на вектор порядка [math]n[/math] в последовательном (наиболее быстром) варианте требуется:
- по [math]n[/math] ярусов умножений и сложений (в каждом из ярусов — [math]m[/math] операций).
При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.
При классификации по высоте ЯПФ, таким образом, алгоритм умножения матрицы на вектор относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.
1.9 Входные и выходные данные алгоритма
Входные данные: алгоритм шифрования, константа [math]c[/math], вероятность характеристики [math]p[/math], число бит раундового ключа [math]b[/math], число раундов шифрования [math]R[/math], входная разница между парами текстов [math]deltafirst[/math], выходная разница между парами текстов [math]deltalast[/math]
Объём входных данных: Объем входных не изменяется, изменяются только сами входные данные.
Выходные данные: Биты раундового ключа последнего раунда.
Объём выходных данных: [math]b[/math].