Участник:Малков Кирилл/Алгоритм бидиагонализации матрицы методом отражений: различия между версиями
| (не показана 21 промежуточная версия этого же участника) | |||
| Строка 5: | Строка 5: | ||
где <math>P</math> и <math>Q</math> - произведения конечного числа матриц отражения(или вращения). | где <math>P</math> и <math>Q</math> - произведения конечного числа матриц отражения(или вращения). | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| − | Пусть дана матрица A размера <math>n \times n</math>. Вычисляется | + | Пусть дана матрица <math>A</math> размера <math>n \times n</math>. Вычисляется бидиагональная матрица <math>D</math> размера <math>n \times n</math>, такая что <math>A = PDQ</math> для некоторых матриц <math>P</math> и <math>Q</math>, являющихся произведением некоторого числа матриц отражения.Сначала мы умножаем A слева на матрицу отражения, аннулирующую все поддиагональные элементы первого столбца. Затем умножаем результат справа на матрицу отражения, аннулирующую элементы первой строки в позициях с 3-й по n-ю. Далее умножением слева аннулируем все поддиагональные элементы второго столбца, затем умножением справа аннулируем получаем нули во второй строке в позициях с 4-й по n-ю и т.д. После каждого умножения на матрицу отражения все ранее полученные нули остаются. |
Формулы метода: | Формулы метода: | ||
| − | Пусть <math>A = [a_1, a_2, ..., a_n]</math> | + | Пусть <math>A = [a_1, a_2, ..., a_n],</math> |
<math>D_1 = A, P_1 = I, Q_1 = I.</math> | <math>D_1 = A, P_1 = I, Q_1 = I.</math> | ||
| − | <math> | + | <br>Если <math>i</math> четное, то <math>D_i = D_{i-1} * (I - 2 * u_{i-1} * u_{i-1}^*)</math> |
| − | <math>u_i = frac{[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]}{||[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]||_2}, Q_i = (I - 2 * u_{i} * u_{i}^*) * Q_{i-1}, P_i = P_{i-1}.</math> | + | <br><math>u_i = \frac{[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]}{||[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]||_2}, Q_i = (I - 2 * u_{i} * u_{i}^*) * Q_{i-1}, P_i = P_{i-1}.</math> |
| − | <math> | + | <br>Если <math>i</math> нечетное, то <math>D_i = (I - 2 * u_{i-1} * u_{i-1}^*) * D_{i-1},</math> |
| − | <math>u_i = frac{[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]}{||[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]||_2}, Q_i = Q_{i-1}, P_i = P_{i-1} * (I - 2 * u_{i} * u_{i}^*).</math> | + | <br><math>u_i = \frac{[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]}{||[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]||_2}, Q_i = Q_{i-1}, P_i = P_{i-1} * (I - 2 * u_{i} * u_{i}^*).</math> |
| + | |||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | Вычислительное ядро алгоритма составляет нахождение на каждом этапе матрицы отражения(всего <math> | + | Вычислительное ядро алгоритма составляет нахождение на каждом этапе матрицы отражения(всего <math>2n - 2</math>). |
| + | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
Операции скалярного произведения, умножения матрицы на вектор | Операции скалярного произведения, умножения матрицы на вектор | ||
| Строка 24: | Строка 26: | ||
<math> для нечетного i : u_i = \frac{[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]}{||[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]||_2}.</math> | <math> для нечетного i : u_i = \frac{[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]}{||[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]||_2}.</math> | ||
=== Последовательная сложность === | === Последовательная сложность === | ||
| − | Для | + | Для бидиагонализации матрицы порядка n методом отражений при последовательном варианте требуется: |
| − | <math>1) 2 * n - 2 вычислений квадратного корня, | + | <math>1) 2 * n - 2</math> вычислений квадратного корня, |
| − | 2) 4 * n - 4 делений, | + | <math>2) 4 * n - 4 </math>делений, |
| − | 3) (4 * n - 4)(1 + n + n^2) умножений, | + | <math>3) (4 * n - 4)(1 + n + n^2)</math> умножений, |
| − | 4) (4 * n - 4)(1 + n + n^2) сложений. | + | <math>4) (4 * n - 4)(1 + n + n^2)</math> сложений. |
| − | Сложность последовательного алгоритма есть <math>O(n^3)< | + | Сложность последовательного алгоритма есть <math>O(n^3)</math>. |
| + | |||
=== Информационный граф === | === Информационный граф === | ||
| − | === При параллельном вычислении двухдиагональной матрицы методом отражений требуется последовательно выполнить следующие ярусы: | + | Информационный граф для количества процессов равного 4. |
| − | < | + | [[Файл:Diagram.png|Информационный граф]] |
| − | -- k ярусов с вычислением (4 * (n/k) - 4)(1 + n + n^2) умножений, | + | <br><math>I-2uu^*</math> - вычисление матрицы отражения; |
| − | -- k ярусов с вычислением (4 * (n/k) - 4)(1 + n + n^2) сложений. | + | <br><math>D, P, Q</math> - умножение матрицы отражения на матрицы D, P, Q; |
| − | Получим, что параллельная сложность алгоритма есть <math>O(n^2)< | + | <br><math>TRANS</math> - транспонирование матрицы D; |
| + | |||
| + | === Ресурс параллелизма алгоритма === | ||
| + | При параллельном вычислении двухдиагональной матрицы методом отражений требуется последовательно выполнить следующие ярусы: | ||
| + | <br>-- k ярусов с вычислением <math>4 * (n/k) - 4</math> делений, | ||
| + | <br>-- k ярусов с вычислением <math>(4 * (n/k) - 4)(1 + n + n^2)</math> умножений, | ||
| + | <br>-- k ярусов с вычислением <math>(4 * (n/k) - 4)(1 + n + n^2)</math> сложений. | ||
| + | <br>Получим, что параллельная сложность алгоритма есть <math>O(n^2)</math>. | ||
| + | |||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | На вход подается матрица A и ее размер n. Выходные данные -- матрицы P, Q, D, такие что <math>A = | + | На вход подается матрица <math>A</math> и ее размер <math>n</math>. Выходные данные -- матрицы <math>P, Q, D,</math> такие что <math>A = PDQ </math> |
| + | |||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным. | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным. | ||
Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна. | Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна. | ||
| + | |||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| + | <source lang="cpp"> | ||
| + | #include <stdio.h> | ||
| + | #include <stdlib.h> | ||
| + | #include <math.h> | ||
| + | #include <mpi.h> | ||
| + | #include <mkl.h> | ||
| + | #include <time.h> | ||
| + | #include <omp.h> | ||
| + | |||
| + | void matrixA_gen(double *A, int num, int n, int m) | ||
| + | { | ||
| + | int r1 = 0, r2 = 0; | ||
| + | for(int i = 0; i < n; i++) | ||
| + | for(int j = 0; j < m; j++) | ||
| + | { | ||
| + | //A[i * m + j] = -1.0 * num * rand() / (double) RAND_MAX * i * j + 2.0 * rand() / (double) RAND_MAX; | ||
| + | A[i*m + j] = i + 1 + num; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | void matrixP_gen(double *P, int num, int n, int m) | ||
| + | { | ||
| + | for(int i = 0; i < n; i++) | ||
| + | { | ||
| + | for(int j = 0; j < m; j++) | ||
| + | { | ||
| + | if((i % m) == j && i >= num * m && i < (num + 1) * m) | ||
| + | { | ||
| + | P[i * m + j] = 1; | ||
| + | } else { | ||
| + | P[i * m + j] = 0; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | double sc_mult(double *a, double *b, int n) | ||
| + | { | ||
| + | double sum = 0; | ||
| + | for(int i = 0; i < n; i++) | ||
| + | sum += a[i] * b[i]; | ||
| + | return sum; | ||
| + | }; | ||
| + | |||
| + | double norm(double *a, int n) | ||
| + | { | ||
| + | return sqrt(sc_mult(a, a, n)); | ||
| + | }; | ||
| + | |||
| + | |||
| + | void mult_vec(double *A, double *u, int n, int m) | ||
| + | { | ||
| + | char t = 'n'; | ||
| + | int int_one = 1; | ||
| + | double *a, one = 1.0, zero = 0.0, min_two = -2.0; | ||
| + | a = (double *)calloc(m, sizeof(*a)); | ||
| + | dgemv(&t, &m, &n, &one, A, &m, u, &int_one, &zero, a, &int_one); | ||
| + | dger(&m, &n, &min_two, a, &int_one, u, &int_one, A, &m); | ||
| + | }; | ||
| + | |||
| + | void mult(double *A, double *B, int l, int n) | ||
| + | { | ||
| + | double *G; | ||
| + | G = (double *)calloc(n * n, sizeof(*G)); | ||
| + | if(l) | ||
| + | { | ||
| + | for(int i = 0; i < n; i++) | ||
| + | for(int j = 0; j < n; j++) | ||
| + | for (int k = 0; k < n; k++) | ||
| + | G[i * n + j] += A[i * n + k] * B[k * n + j]; | ||
| + | } else { | ||
| + | for(int i = 0; i < n; i++) | ||
| + | for(int j = 0; j < n; j++) | ||
| + | for (int k = 0; k < n; k++) | ||
| + | G[i * n + j] += B[i * n + k] * A[k * n + j]; | ||
| + | } | ||
| + | for (int i = 0; i < n; i++) | ||
| + | for(int j = 0; j < n; j++) | ||
| + | A[i*n + j] = G[i*n +j]; | ||
| + | free(G); | ||
| + | }; | ||
| + | |||
| + | |||
| + | void reflect(double *u, double *a, int n, int j) | ||
| + | { | ||
| + | for (int i = 0; i < n; i++) | ||
| + | { | ||
| + | if (i < j) | ||
| + | { | ||
| + | u[i] = 0; | ||
| + | } else { | ||
| + | if (i == j){ | ||
| + | u[i] = a[i] - norm(a, n); | ||
| + | } else { | ||
| + | u[i] = a[i]; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | double sc = norm(u, n); | ||
| + | if(sc != 0) | ||
| + | { | ||
| + | for(int i = 0; i < n; i++) | ||
| + | { | ||
| + | u[i] /= sc; | ||
| + | } | ||
| + | } | ||
| + | }; | ||
| + | |||
| + | void trans(double *A, int n) | ||
| + | { | ||
| + | double *B; | ||
| + | B = (double *) calloc(n * n, sizeof(*B)); | ||
| + | for(int i = 0; i < n; i++) | ||
| + | for(int j = 0; j < n; j++) | ||
| + | B[i * n + j] = A[j * n + i]; | ||
| + | for(int i = 0; i < n; i++) | ||
| + | for(int j = 0; j < n; j++) | ||
| + | A[i * n + j] = B[i * n + j]; | ||
| + | free(B); | ||
| + | return; | ||
| + | } | ||
| + | |||
| + | int main(int argc, char **argv) | ||
| + | { | ||
| + | MPI_Init(&argc, &argv); | ||
| + | int size, num, error, n, m, i = 0; | ||
| + | double d_norm = 0; | ||
| + | MPI_Comm_size(MPI_COMM_WORLD, &size); | ||
| + | MPI_Comm_rank(MPI_COMM_WORLD, &num); | ||
| + | n = 64; | ||
| + | srand(time(NULL)); | ||
| + | if(size != 0) | ||
| + | { | ||
| + | m = n/size; | ||
| + | } | ||
| + | MPI_Request req; | ||
| + | MPI_Status status; | ||
| + | double *M, *A, *P, *Q, *C, *D, *Df, *Pf, *Qf, *V, *A1, *W; | ||
| + | double *u, *a; | ||
| + | A1 = (double *) calloc(m * n, sizeof(*A1)); | ||
| + | V = (double *)calloc(n * n, sizeof(*V)); | ||
| + | W = (double *)calloc(n * n, sizeof(*W)); | ||
| + | Qf = (double *)calloc(n * n, sizeof(*Qf)); | ||
| + | M = (double *)calloc(n * n, sizeof(*M)); | ||
| + | Pf = (double *)calloc(n * n, sizeof(*Pf)); | ||
| + | A = (double *)calloc(n * m, sizeof(*A)); | ||
| + | P = (double *)calloc(n * m, sizeof(*P)); | ||
| + | Q = (double *)calloc(n * m, sizeof(*Q)); | ||
| + | C = (double *)calloc(m * m, sizeof(*C)); | ||
| + | D = (double *)calloc(n * n, sizeof(*D)); | ||
| + | Df = (double *)calloc(n * n, sizeof(*Df)); | ||
| + | u = (double *)calloc(n, sizeof(*u)); | ||
| + | a = (double *)calloc(n, sizeof(*a)); | ||
| + | matrixA_gen(A, num, n, m); | ||
| + | matrixP_gen(P, num, n, m); | ||
| + | matrixP_gen(Q, num, n, m); | ||
| + | MPI_Gather(A, n * m, MPI_DOUBLE, D, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD); | ||
| + | if(num == 0) | ||
| + | { | ||
| + | for(int k = 0; k < size; k++) | ||
| + | for(int j = 0; j < n; j++) | ||
| + | for(int h = 0; h < m; h++) | ||
| + | { | ||
| + | M[h + k * m + j * n] = D[k * m * n + j * m + h]; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | double t1 = MPI_Wtime(); | ||
| + | |||
| + | for(int f = 0; f < 2 * n - 2; f++) | ||
| + | { | ||
| + | i = f / 2; | ||
| + | if(i < num * m || i >= (num + 1) * m ) | ||
| + | { | ||
| + | MPI_Recv(u, n, MPI_DOUBLE, (i / m), 0, MPI_COMM_WORLD, &status); | ||
| + | mult_vec(A, u, n, m); | ||
| + | if(!(f%2)) | ||
| + | mult_vec(P, u, n, m); | ||
| + | else | ||
| + | mult_vec(Q, u, n, m); | ||
| + | } else { | ||
| + | if(!(f%2)) | ||
| + | { | ||
| + | for(int k = 0; k < n; k++) | ||
| + | { | ||
| + | if(k < i) | ||
| + | { | ||
| + | a[k] = 0; | ||
| + | } else { | ||
| + | a[k] = A[(i % m) + k * m]; | ||
| + | } | ||
| + | } | ||
| + | reflect(u, a, n, i); | ||
| + | for(int l = 0; l < size; l++) | ||
| + | { | ||
| + | if(l != num) | ||
| + | { | ||
| + | MPI_Isend(u, n, MPI_DOUBLE, l, 0, MPI_COMM_WORLD, &req); | ||
| + | } | ||
| + | } | ||
| + | } else { | ||
| + | for(int k = 0; k < n; k++) | ||
| + | { | ||
| + | if(k < i+1) | ||
| + | { | ||
| + | a[k] = 0; | ||
| + | } else { | ||
| + | a[k] = A[(i % m) + k * m]; | ||
| + | } | ||
| + | } | ||
| + | reflect(u, a, n, i+1); | ||
| + | for(int l = 0; l < size; l++) | ||
| + | { | ||
| + | if(l != num) | ||
| + | { | ||
| + | MPI_Isend(u, n, MPI_DOUBLE, l, 0, MPI_COMM_WORLD, &req); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | mult_vec(A, u, n, m); | ||
| + | if(!(f%2)) | ||
| + | mult_vec(P, u, n, m); | ||
| + | else | ||
| + | mult_vec(Q, u, n, m); | ||
| + | } | ||
| + | for(int k = 0; k < n; k++) | ||
| + | for(int j = 0; j < m; j++) | ||
| + | A1[k * m + j] = A[k * m + j]; | ||
| + | |||
| + | for(int j = 0; j < size; j++) | ||
| + | { | ||
| + | if(j != num) | ||
| + | { | ||
| + | for(int l = 0; l < m; l++) | ||
| + | for(int h = 0; h < m; h++) | ||
| + | C[h * m + l] = A1[j * m * m + h + l * m]; | ||
| + | MPI_Isend(C, m * m, MPI_DOUBLE, j, 0, MPI_COMM_WORLD, &req); | ||
| + | } else { | ||
| + | for(int l = 0; l < m; l++) | ||
| + | for(int h = 0; h < m; h++) | ||
| + | C[h * m + l] = A1[j * m * m + h + l * m]; | ||
| + | |||
| + | for(int l = 0; l < m; l++) | ||
| + | for(int h = 0; h < m; h++) | ||
| + | A1[j * m * m + h + l * m] = C[h + l * m]; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | for(int k = 0; k < size; k++) | ||
| + | { | ||
| + | if(k != num) | ||
| + | { | ||
| + | MPI_Recv(C, m * m, MPI_DOUBLE, k, 0, MPI_COMM_WORLD, &status); | ||
| + | |||
| + | for(int l = 0; l < m; l++) | ||
| + | { | ||
| + | for(int h = 0; h < m; h++) | ||
| + | { | ||
| + | A1[k * m * m + l + h * m] = C[h * m + l]; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | for(int k = 0; k < n; k++) | ||
| + | for(int j = 0; j < m; j++) | ||
| + | A[k * m + j] = A1[k * m + j]; | ||
| + | } | ||
| + | double t2 = MPI_Wtime(); | ||
| + | MPI_Gather(P, n * m, MPI_DOUBLE, D, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD); | ||
| + | MPI_Gather(Q, n * m, MPI_DOUBLE, W, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD); | ||
| + | MPI_Gather(A, n * m, MPI_DOUBLE, V, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD); | ||
| + | return 0; | ||
| + | } | ||
| + | </source> | ||
| + | |||
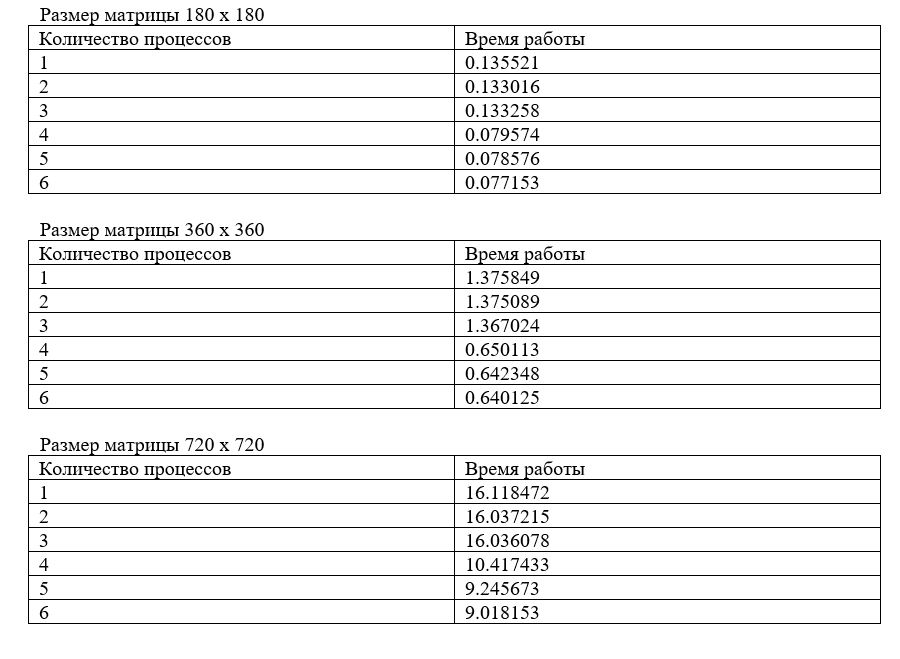
| + | [[Файл:Безымянный777.png|Результаты тестирования алгоритма на кластере ИВМ РАН]] | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| + | Для оптимальности работы алгоритма следует реализовать функцию умножения матрицы отражения матрицы отражения на произвольную матрицу, это заметно сократит время время его работы. | ||
=== Локальность данных и вычислений === | === Локальность данных и вычислений === | ||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | Алгоритм бидиагонализации матрицы довольно последователен: на каждом шаге считается матрица отражения, и распараллелить прямым образом алгоритм нельзя, поскольку каждый раз матрица отражения строится к новой матрице. Однако можно разбить Матрицу <math> D</math> на блоки, и каждый процесс будет занят умножением матрицы отражения на соответствующий блок. | ||
| + | |||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | === Существующие реализации | + | Параллельная реализация алгоритма наиболее эффективна на машинах с быстрым обменом данных меду процессами |
| + | === Существующие реализации алгоритма === | ||
== Литература == | == Литература == | ||
Е. Е. Тыртышников, "Методы численного анализа". | Е. Е. Тыртышников, "Методы численного анализа". | ||
Текущая версия на 23:43, 12 декабря 2021
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Матрица [math]B = [b_{ij}][/math] называется (верхней) двухдиагональной, или бидиагональной, если [math]b_{ij} = 0[/math], [math]i \gt j[/math] или [math]i + 1 \lt j[/math]. Алгоритм бидиагонализации матрицы методом отражений приводит произвольную [math]n \times n[/math] матрицу A к бидиагональному виду [math]B = PAQ[/math], где [math]P[/math] и [math]Q[/math] - произведения конечного числа матриц отражения(или вращения).
1.2 Математическое описание алгоритма
Пусть дана матрица [math]A[/math] размера [math]n \times n[/math]. Вычисляется бидиагональная матрица [math]D[/math] размера [math]n \times n[/math], такая что [math]A = PDQ[/math] для некоторых матриц [math]P[/math] и [math]Q[/math], являющихся произведением некоторого числа матриц отражения.Сначала мы умножаем A слева на матрицу отражения, аннулирующую все поддиагональные элементы первого столбца. Затем умножаем результат справа на матрицу отражения, аннулирующую элементы первой строки в позициях с 3-й по n-ю. Далее умножением слева аннулируем все поддиагональные элементы второго столбца, затем умножением справа аннулируем получаем нули во второй строке в позициях с 4-й по n-ю и т.д. После каждого умножения на матрицу отражения все ранее полученные нули остаются.
Формулы метода:
Пусть [math]A = [a_1, a_2, ..., a_n],[/math]
[math]D_1 = A, P_1 = I, Q_1 = I.[/math]
Если [math]i[/math] четное, то [math]D_i = D_{i-1} * (I - 2 * u_{i-1} * u_{i-1}^*)[/math]
[math]u_i = \frac{[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]}{||[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]||_2}, Q_i = (I - 2 * u_{i} * u_{i}^*) * Q_{i-1}, P_i = P_{i-1}.[/math]
Если [math]i[/math] нечетное, то [math]D_i = (I - 2 * u_{i-1} * u_{i-1}^*) * D_{i-1},[/math]
[math]u_i = \frac{[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]}{||[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]||_2}, Q_i = Q_{i-1}, P_i = P_{i-1} * (I - 2 * u_{i} * u_{i}^*).[/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма составляет нахождение на каждом этапе матрицы отражения(всего [math]2n - 2[/math]).
1.4 Макроструктура алгоритма
Операции скалярного произведения, умножения матрицы на вектор
1.5 Схема реализации последовательного алгоритма
[math]D_1 = A, P_1 = I, Q_1 = I.[/math] [math]1) для четного i : D_i = D_{i-1} * (I - 2 * u_{i-1} * u_{i-1}^*), Q_i = (I - 2 * u_{i} * u_{i}^*) * Q_{i-1}, P_i = P_{i-1};[/math] [math] для нечетного i : D_i = (I - 2 * u_{i-1} * u_{i-1}^*) * D_{i-1}, Q_i = Q_{i-1}, P_i = P_{i-1} * (I - 2 * u_{i} * u_{i}^*).[/math] [math]2) для четного i : u_i = \frac{[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]}{||[0, 0, ..., 0, d_{i+1} - ||d_{i+1}||_2, d_{i+2}, ..., d_n]||_2},[/math] [math] для нечетного i : u_i = \frac{[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]}{||[0, 0, ..., 0, d_i - ||d_i||_2, d_{i+1}, ..., d_n]||_2}.[/math]
1.6 Последовательная сложность
Для бидиагонализации матрицы порядка n методом отражений при последовательном варианте требуется: [math]1) 2 * n - 2[/math] вычислений квадратного корня, [math]2) 4 * n - 4 [/math]делений, [math]3) (4 * n - 4)(1 + n + n^2)[/math] умножений, [math]4) (4 * n - 4)(1 + n + n^2)[/math] сложений. Сложность последовательного алгоритма есть [math]O(n^3)[/math].
1.7 Информационный граф
Информационный граф для количества процессов равного 4.
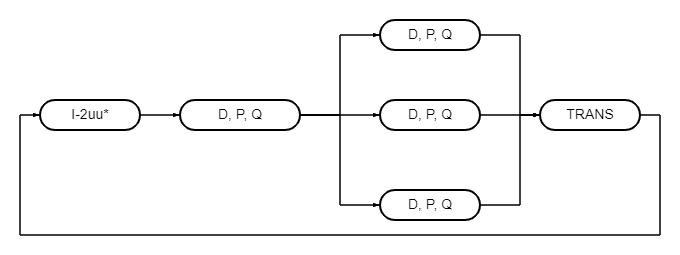
[math]I-2uu^*[/math] - вычисление матрицы отражения;
[math]D, P, Q[/math] - умножение матрицы отражения на матрицы D, P, Q;
[math]TRANS[/math] - транспонирование матрицы D;
1.8 Ресурс параллелизма алгоритма
При параллельном вычислении двухдиагональной матрицы методом отражений требуется последовательно выполнить следующие ярусы:
-- k ярусов с вычислением [math]4 * (n/k) - 4[/math] делений,
-- k ярусов с вычислением [math](4 * (n/k) - 4)(1 + n + n^2)[/math] умножений,
-- k ярусов с вычислением [math](4 * (n/k) - 4)(1 + n + n^2)[/math] сложений.
Получим, что параллельная сложность алгоритма есть [math]O(n^2)[/math].
1.9 Входные и выходные данные алгоритма
На вход подается матрица [math]A[/math] и ее размер [math]n[/math]. Выходные данные -- матрицы [math]P, Q, D,[/math] такие что [math]A = PDQ [/math]
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным. Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна.
2 Программная реализация алгоритма
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <mpi.h>
#include <mkl.h>
#include <time.h>
#include <omp.h>
void matrixA_gen(double *A, int num, int n, int m)
{
int r1 = 0, r2 = 0;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
{
//A[i * m + j] = -1.0 * num * rand() / (double) RAND_MAX * i * j + 2.0 * rand() / (double) RAND_MAX;
A[i*m + j] = i + 1 + num;
}
}
void matrixP_gen(double *P, int num, int n, int m)
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
if((i % m) == j && i >= num * m && i < (num + 1) * m)
{
P[i * m + j] = 1;
} else {
P[i * m + j] = 0;
}
}
}
}
double sc_mult(double *a, double *b, int n)
{
double sum = 0;
for(int i = 0; i < n; i++)
sum += a[i] * b[i];
return sum;
};
double norm(double *a, int n)
{
return sqrt(sc_mult(a, a, n));
};
void mult_vec(double *A, double *u, int n, int m)
{
char t = 'n';
int int_one = 1;
double *a, one = 1.0, zero = 0.0, min_two = -2.0;
a = (double *)calloc(m, sizeof(*a));
dgemv(&t, &m, &n, &one, A, &m, u, &int_one, &zero, a, &int_one);
dger(&m, &n, &min_two, a, &int_one, u, &int_one, A, &m);
};
void mult(double *A, double *B, int l, int n)
{
double *G;
G = (double *)calloc(n * n, sizeof(*G));
if(l)
{
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
for (int k = 0; k < n; k++)
G[i * n + j] += A[i * n + k] * B[k * n + j];
} else {
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
for (int k = 0; k < n; k++)
G[i * n + j] += B[i * n + k] * A[k * n + j];
}
for (int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
A[i*n + j] = G[i*n +j];
free(G);
};
void reflect(double *u, double *a, int n, int j)
{
for (int i = 0; i < n; i++)
{
if (i < j)
{
u[i] = 0;
} else {
if (i == j){
u[i] = a[i] - norm(a, n);
} else {
u[i] = a[i];
}
}
}
double sc = norm(u, n);
if(sc != 0)
{
for(int i = 0; i < n; i++)
{
u[i] /= sc;
}
}
};
void trans(double *A, int n)
{
double *B;
B = (double *) calloc(n * n, sizeof(*B));
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
B[i * n + j] = A[j * n + i];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
A[i * n + j] = B[i * n + j];
free(B);
return;
}
int main(int argc, char **argv)
{
MPI_Init(&argc, &argv);
int size, num, error, n, m, i = 0;
double d_norm = 0;
MPI_Comm_size(MPI_COMM_WORLD, &size);
MPI_Comm_rank(MPI_COMM_WORLD, &num);
n = 64;
srand(time(NULL));
if(size != 0)
{
m = n/size;
}
MPI_Request req;
MPI_Status status;
double *M, *A, *P, *Q, *C, *D, *Df, *Pf, *Qf, *V, *A1, *W;
double *u, *a;
A1 = (double *) calloc(m * n, sizeof(*A1));
V = (double *)calloc(n * n, sizeof(*V));
W = (double *)calloc(n * n, sizeof(*W));
Qf = (double *)calloc(n * n, sizeof(*Qf));
M = (double *)calloc(n * n, sizeof(*M));
Pf = (double *)calloc(n * n, sizeof(*Pf));
A = (double *)calloc(n * m, sizeof(*A));
P = (double *)calloc(n * m, sizeof(*P));
Q = (double *)calloc(n * m, sizeof(*Q));
C = (double *)calloc(m * m, sizeof(*C));
D = (double *)calloc(n * n, sizeof(*D));
Df = (double *)calloc(n * n, sizeof(*Df));
u = (double *)calloc(n, sizeof(*u));
a = (double *)calloc(n, sizeof(*a));
matrixA_gen(A, num, n, m);
matrixP_gen(P, num, n, m);
matrixP_gen(Q, num, n, m);
MPI_Gather(A, n * m, MPI_DOUBLE, D, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD);
if(num == 0)
{
for(int k = 0; k < size; k++)
for(int j = 0; j < n; j++)
for(int h = 0; h < m; h++)
{
M[h + k * m + j * n] = D[k * m * n + j * m + h];
}
}
double t1 = MPI_Wtime();
for(int f = 0; f < 2 * n - 2; f++)
{
i = f / 2;
if(i < num * m || i >= (num + 1) * m )
{
MPI_Recv(u, n, MPI_DOUBLE, (i / m), 0, MPI_COMM_WORLD, &status);
mult_vec(A, u, n, m);
if(!(f%2))
mult_vec(P, u, n, m);
else
mult_vec(Q, u, n, m);
} else {
if(!(f%2))
{
for(int k = 0; k < n; k++)
{
if(k < i)
{
a[k] = 0;
} else {
a[k] = A[(i % m) + k * m];
}
}
reflect(u, a, n, i);
for(int l = 0; l < size; l++)
{
if(l != num)
{
MPI_Isend(u, n, MPI_DOUBLE, l, 0, MPI_COMM_WORLD, &req);
}
}
} else {
for(int k = 0; k < n; k++)
{
if(k < i+1)
{
a[k] = 0;
} else {
a[k] = A[(i % m) + k * m];
}
}
reflect(u, a, n, i+1);
for(int l = 0; l < size; l++)
{
if(l != num)
{
MPI_Isend(u, n, MPI_DOUBLE, l, 0, MPI_COMM_WORLD, &req);
}
}
}
mult_vec(A, u, n, m);
if(!(f%2))
mult_vec(P, u, n, m);
else
mult_vec(Q, u, n, m);
}
for(int k = 0; k < n; k++)
for(int j = 0; j < m; j++)
A1[k * m + j] = A[k * m + j];
for(int j = 0; j < size; j++)
{
if(j != num)
{
for(int l = 0; l < m; l++)
for(int h = 0; h < m; h++)
C[h * m + l] = A1[j * m * m + h + l * m];
MPI_Isend(C, m * m, MPI_DOUBLE, j, 0, MPI_COMM_WORLD, &req);
} else {
for(int l = 0; l < m; l++)
for(int h = 0; h < m; h++)
C[h * m + l] = A1[j * m * m + h + l * m];
for(int l = 0; l < m; l++)
for(int h = 0; h < m; h++)
A1[j * m * m + h + l * m] = C[h + l * m];
}
}
for(int k = 0; k < size; k++)
{
if(k != num)
{
MPI_Recv(C, m * m, MPI_DOUBLE, k, 0, MPI_COMM_WORLD, &status);
for(int l = 0; l < m; l++)
{
for(int h = 0; h < m; h++)
{
A1[k * m * m + l + h * m] = C[h * m + l];
}
}
}
}
for(int k = 0; k < n; k++)
for(int j = 0; j < m; j++)
A[k * m + j] = A1[k * m + j];
}
double t2 = MPI_Wtime();
MPI_Gather(P, n * m, MPI_DOUBLE, D, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Gather(Q, n * m, MPI_DOUBLE, W, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Gather(A, n * m, MPI_DOUBLE, V, n * m, MPI_DOUBLE, 0, MPI_COMM_WORLD);
return 0;
}
2.1 Особенности реализации последовательного алгоритма
Для оптимальности работы алгоритма следует реализовать функцию умножения матрицы отражения матрицы отражения на произвольную матрицу, это заметно сократит время время его работы.
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
Алгоритм бидиагонализации матрицы довольно последователен: на каждом шаге считается матрица отражения, и распараллелить прямым образом алгоритм нельзя, поскольку каждый раз матрица отражения строится к новой матрице. Однако можно разбить Матрицу [math] D[/math] на блоки, и каждый процесс будет занят умножением матрицы отражения на соответствующий блок.
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
Параллельная реализация алгоритма наиболее эффективна на машинах с быстрым обменом данных меду процессами
2.7 Существующие реализации алгоритма
3 Литература
Е. Е. Тыртышников, "Методы численного анализа".