Уровень алгоритма

Алгоритм Борувки: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
[непроверенная версия][досмотренная версия]
 
(не показана 61 промежуточная версия 7 участников)
Строка 1: Строка 1:
−
== Свойства и структура алгоритмов ==
+
{{algorithm
 +
| name              = Алгоритм Борувки
 +
| serial_complexity = <math>O(|E|ln(|V|))</math>
 +
| pf_height        = <math>max O(ln(|V|)) </math>
 +
| pf_width          = <math>O(|E|)</math>
 +
| input_data        = <math>O(|V| + |E|)</math>
 +
| output_data      = <math>O(|V|)</math>
 +
}}
 +
 
 +
== Свойства и структура алгоритма ==
 
=== Общее описание алгоритма ===
 
=== Общее описание алгоритма ===
  
 
'''Алгоритм Борувки'''<ref>Borůvka, Otakar. “O Jistém Problému Minimálním.” Práce Moravské Přírodovědecké Společnosti III, no. 3 (1926): 37–58.</ref><ref>Jarník, Vojtěch. “O Jistém Problému Minimálním (Z Dopisu Panu O. Borůvkovi).” Práce Moravské Přírodovědecké Společnosti 6, no. 4 (1930): 57–63.</ref> предназначен для решения [[Построение минимального остовного дерева (MST)|задачи о построении минимального остовного дерева]] во взвешенном неориентированном графе. Алгоритм хорошо параллелизуется и является основой для распределённого [[Алгоритм GHS|алгоритма GHS]].
 
'''Алгоритм Борувки'''<ref>Borůvka, Otakar. “O Jistém Problému Minimálním.” Práce Moravské Přírodovědecké Společnosti III, no. 3 (1926): 37–58.</ref><ref>Jarník, Vojtěch. “O Jistém Problému Minimálním (Z Dopisu Panu O. Borůvkovi).” Práce Moravské Přírodovědecké Společnosti 6, no. 4 (1930): 57–63.</ref> предназначен для решения [[Построение минимального остовного дерева (MST)|задачи о построении минимального остовного дерева]] во взвешенном неориентированном графе. Алгоритм хорошо параллелизуется и является основой для распределённого [[Алгоритм GHS|алгоритма GHS]].
  
−
=== Математическое описание ===
+
=== Математическое описание алгоритма ===
 +
 
 +
Пусть задан связный неориентированный граф <math>G = (V, E)</math> с весами рёбер <math>f(e)</math>. Предполагается, что веса всех рёбер различны (если это не так, то можно упорядочить рёбра сначала по весу, а потом по номеру).
 +
 
 +
Алгоритм Борувки основан на следующих двух свойствах задачи:
 +
* '''Минимальное ребро фрагмента'''. Пусть <math>F</math> – фрагмент минимального остовного дерева и <math>e_F</math> – ребро наименьшего веса, исходящее из <math>F</math> (т.е. ровно один его конец является вершиной из <math>F</math>). Если ребро <math>e_F</math> единственно, то оно принадлежит минимальному остовному дереву.
 +
* '''Схлопывание фрагментов'''. Пусть <math>F</math> – фрагмент минимального остовного дерева графа <math>G</math>, а граф <math>G'</math> получен из <math>G</math> склеиванием вершин, принадлежащих <math>F</math>. Тогда объединение <math>F</math> и минимального остовного дерева графа <math>G'</math> даёт минимальное остовное дерево исходного графа <math>G</math>.
 +
 
 +
В начале работы алгоритма каждая вершина графа <math>G</math> является отдельным фрагментом. На очередном шаге у каждого фрагмента выбирается исходящее ребро минимального веса (если такое ребро существует). Выбранные рёбра добавляются в минимальное остовное дерево, а соответствующие фрагменты склеиваются.
 +
 
 
=== Вычислительное ядро алгоритма ===
 
=== Вычислительное ядро алгоритма ===
 +
Основными операциями являются:
 +
# Поиск минимального по весу исходящего ребра в каждом фрагменте.
 +
# Объединение фрагментов.
 +
 
=== Макроструктура алгоритма ===
 
=== Макроструктура алгоритма ===
−
=== Описание схемы реализации последовательного алгоритма ===
+
В задаче требуется указать в данном связном взвешенном графе дерево, соединяющее все его вершины и имеющее наименьший возможный суммарный вес рёбер.
 +
 
 +
Классический пример (из статьи Борувки) – спроектировать наиболее дешёвую электрическую сеть, зная стоимость устройства каждого участка электрической линии.
 +
 
 +
Пусть задан связный граф <math>G=(V,E)</math> с вершинами <math>V = ( v_{1}, v_{2}, ..., v_{n} )</math> и рёбрами <math>E = ( e_{1}, e_{2}, ..., e_{m} )</math>. Каждому ребру <math>e \in E</math> приписан вес <math>w(e)</math>.
 +
 
 +
Требуется построить дерево <math>T^* \subseteq E</math>, связывающее все вершины и имеющее наименьший возможный вес среди всех таких деревьев:
 +
 
 +
<math> w(T^* )= \min_T( w(T)) </math>
 +
 
 +
где вес множества рёбер есть сумма их весов:
 +
 
 +
<math>w(T)=\sum_{e \in T} (w(T))</math>
 +
 
 +
Если граф <math>G</math> не является связным, то дерева, связывающего все вершины, не существует.
 +
 
 +
В этом случае необходимо найти минимальной остовное дерево для каждой компоненты связности <math>G</math>. Набор таких деревьев называется минимальным остовным лесом (сокращённо MSF – Minimum Spanning Forest).
 +
 
 +
==== Вспомогательный алгоритм: система непересекающихся множеств (Union-Find)====
 +
 
 +
Во всех алгоритмах решения задачи требуется отслеживать, каким уже построенным фрагментам дерева принадлежат те или иные вершины графа. Для этого используется структура данных «система непересекающихся множеств» (Union-Find). Данная структура поддерживает две операции:
 +
 
 +
1. <math>FIND(v) = w</math> – по вершине v возвращает вершину w – «корень» фрагмента, которому принадлежит вершина v. При этом гарантируется, что вершины u и v принадлежат одному и тому же фрагменту, тогда и только тогда, когда <math>FIND(u) = FIND(v)</math>.
 +
 
 +
2. <math>MERGE(u, v)</math> – объединяет два фрагмента, которым принадлежат вершины <math>u</math> и <math>v.</math> (Если они уже лежат в одном фрагменте, то ничего не происходит.) При практической реализации удобно, чтобы данная операция возвращала значение истина, если объединение фрагментов имело место, и ложь в противном случае.
 +
 
 +
==== Последовательная версия====
 +
 
 +
Классический последовательный алгоритм Union-Find описан в статье Тарьяна. Каждой вершине v приписывается указатель на вершину-родителя <math>parent(v)</math>.
 +
 
 +
1. Изначально <math>parent(v) := v</math> для всех вершин.
 +
 
 +
2. <math>FIND(v)</math> выполняется следующим образом: полагаем <math>u := v</math>, и далее следуем по указателям <math>u := parent(u)</math> до тех пор, пока не станет <math>u = parent(u)</math>. Это и будет результат операции. Дополнительно можно «схлопывать» дерево: присвоить всем посещённым вершинами: <math>parent(u_i) := u</math>, либо производить схлопывание по пути: <math>parent(u) := parent(parent(u)))</math>.
 +
 
 +
3. <math>MERGE(u, v)</math> выполняется следующим образом: вначале находим корневые вершины <math>u := FIND(u), v := FIND(v)</math>. Если <math>u = v</math>, то исходные вершины принадлежат одному фрагменту и объединения фрагментов не происходит. В противном случае полагаем одно из <math>parent(u) := v</math> или <math>parent(v) := u</math>. Дополнительно можно отслеживать количество вершин в каждом из фрагментов, чтобы меньший фрагмент подсоединять к большему, а не наоборот (оценки сложности доказываются именно при такой реализации, однако на практике алгоритм хорошо работает и без подсчёта количества вершин).
 +
 
 +
=== Схема реализации последовательного алгоритма ===
 +
В алгоритме Борувки фрагменты минимального остовного дерева наращиваются постепенно присоединением минимального ребра, выходящего из каждого фрагмента.
 +
 
 +
1. В самом начале каждая вершина является отдельным фрагментом.
 +
 
 +
2. На каждом шаге:
 +
 
 +
* Для каждого фрагмента определяется минимальное по весу исходящее ребро.
 +
 
 +
* Минимальные рёбра добавляются в минимальное остовное дерево, а соответствующие фрагменты объединяются.
 +
 
 +
3. Алгоритм останавливается, когда остаётся только один фрагмент либо когда ни у одного из фрагментов нет исходящих рёбер.
 +
 
 +
Поиск минимальных исходящих рёбер может выполняться независимо для каждого фрагмента. Таким образом, данную стадию вычислений можно эффективно параллелизовать (в том числе с использованием массового параллелизма графических ускорителей).
 +
 
 +
Объединение фрагментов также может быть реализовано параллельно с использованием параллельной версии описанного выше алгоритма Union-Find.
 +
 
 +
Аккуратный подсчёт количества активных фрагментов позволяет остановить алгоритм Борувки на один шаг раньше обычного:
 +
 
 +
1. В начале итерации счётчик активных фрагментов обнуляется.
 +
 
 +
2. На этапе поиска минимальных рёбер счётчик увеличивается на единицу для каждого фрагмента, у которого были исходящие рёбра.
 +
 
 +
3. На этапе объединения фрагментов счётчик уменьшается на единицу каждый раз, когда операция <math>MERGE(u, v)</math> вернула значение истина.
 +
 
 +
Если в конце итерации счётчик равен 0 или 1, то вычисления останавливаются.
 +
Параллелизм возможен на этапе сортировки рёбер по весу, однако основной ход алгоритма является последовательным.
 +
 
 
=== Последовательная сложность алгоритма ===
 
=== Последовательная сложность алгоритма ===
 +
Последовательная сложность алгоритма Борувки для графа с <math>|V|</math> вершинами и <math>|E|</math> рёбрами составляет <math>O(|E| \ln(|V|))</math> операций.
 +
 
=== Информационный граф ===
 
=== Информационный граф ===
−
=== Описание ресурса параллелизма алгоритма ===
+
 
−
=== Описание входных и выходных данных ===
+
В описанном подходе существует два уровня параллелизма: параллелизм в классическом алгоритме Борувки (нижний) и параллелизм в алгоритме обработки графа, не помещающегося в память.
−
=== Свойства алгоритма===
+
−
== Программная реализация алгоритмов ==
+
'''Нижний уровень параллелизма''': поиск минимальных исходящих рёбер может выполняться независимо для каждого фрагмента, благодаря чему данную стадию вычислений можно эффективно параллелизовать (как на GPU, так и на CPU). Объединение фрагментов также может быть реализовано параллельно с использованием описанного выше алгоритма Union-Find.
 +
 
 +
'''Верхний уровень параллелизма''': построение отдельных минимальных основных деревьев для каждого из списков ребер может производиться параллельно. Например, список ребер может разбиваться на две части, одна из которых обрабатывается на GPU, а вторая параллельно на CPU.
 +
 
 +
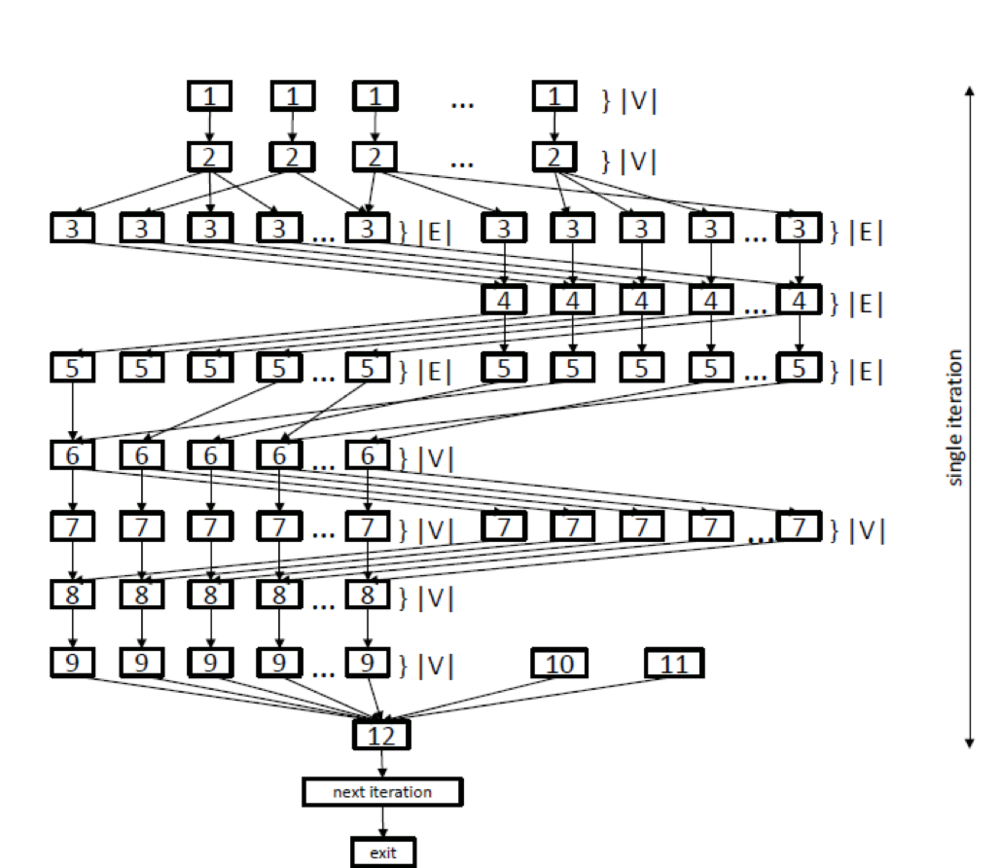
[[file:MST low.png|thumb|center|1000px|Рисунок 1. Информационный граф нижнего уровня параллелизма]]
 +
 
 +
Рассмотрим информационные графы и подробное описание каждого из них. Также можно считать, что на рисунке 1 представлен информационный граф классического алгоритма Борувки, а на рисунке 2 — алгоритма обработки графа.
 +
 
 +
Нижний уровень параллелизма на графе алгоритма (рисунок 1) расположен на уровнях {3, 4, 5}, соответствующих операциям параллельного поиска минимальных исходящих ребер, а также на уровнях {6, 7, 8}, соответствующих операциям параллельного объединения деревьев. Также  различные операции копирования {1, 2, 8, 9} выполняются параллельно. После выполнения тела цикла производится проверка {12} того, сколько деревьев осталось на текущем шаге, и если данное число не изменилось, то происходит выход из цикла, иначе переход к следующей итерации.
 +
 
 +
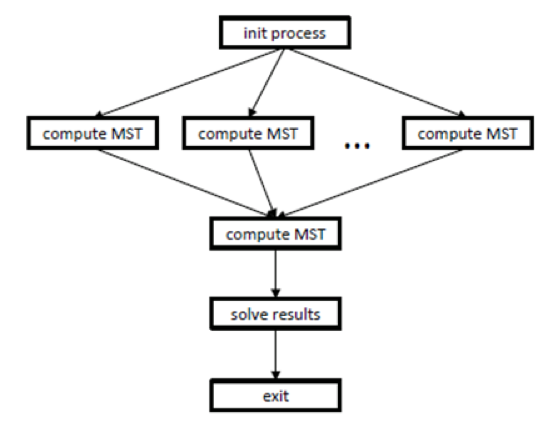
Верхний уровень параллелизма (рисунок 2), как уже говорилось, заключается в параллельном вычислении минимального остовного дерева (compute mst) для различных частей графа. Перед этим производится процесс инициализации (init process), данные которого используют последующие параллельные операции compute mst. Затем, после параллельных вычислений mst, происходит вычисление итогового основного дерева, после чего полученный результат сохраняется (save results).
 +
 
 +
[[file:MST up.png|thumb|center|1000px|Рисунок 2. Информационный граф верхнего уровня параллелизма]]
 +
 
 +
=== Ресурс параллелизма алгоритма ===
 +
 
 +
Итак, алгоритм Борувки обладает двумя уровнями параллелизма.
 +
 
 +
На верхнем уровне минимальные остовные деревья могут искаться для отдельных частей списка ребер графа (параллельные compute_MST на рисунке 2). Однако затем должно последовать финальное объединение полученных ребер и вычисление минимального остовного дерева для полученного графа, которое будет производиться последовательно.
 +
 
 +
Кроме того, вычисление каждого из минимальных остовных деревьев (параллельные compute_MST на рисунке 2) обладает внутренним ресурсом параллелизма, описанным далее. Операции инициализации и копирования данных ([1], [2], [9]  на рисунке 1) могут производиться параллельно за <math>O(|V|)</math> операций. Также параллельно могут производиться операции поиска минимальных исходящих ребер ([3],[4],[5]), при этом для каждой дуги и обратной к ней независимо, что даёт <math>2*O(|E|)</math> параллельных операций. Помимо этого, операции объединения деревьев [6], [7], [8] могут также производиться параллельно за <math>O(|V|)</math> операций.
 +
 
 +
В результате для классического алгоритма Борувки ширина ярусно-параллельной формы равна <math>O(|E|)</math>, а высота ЯПФ зависит от числа шагов алгоритма и ограничена сверху <math>O(ln(|V|))</math>.
 +
 
 +
=== Входные и выходные данные алгоритма ===
 +
'''Входные данные''': взвешенный граф <math>(V, E, W)</math> (<math>|V|</math> вершин <math>v_i</math> и <math>|E|</math> рёбер <math>e_j = (v^{(1)}_{j},
 +
v^{(2)}_{j})</math> с весами <math>f_j</math>).
 +
 
 +
'''Объём входных данных''': <math>O(|V| + |E|)</math>.
 +
 
 +
'''Выходные данные''': список рёбер минимального остовного дерева (для несвязного графа – список минимальных остовных деревьев для всех компонент связности).
 +
 
 +
'''Объём выходных данных''': <math>O(|V|)</math>.
 +
 
 +
=== Свойства алгоритма ===
 +
# Алгоритм останавливается за конечное число шагов, поскольку на каждом шаге становится по крайней мере на один фрагмент меньше.
 +
# Более того, число фрагментов на каждом шаге уменьшается как минимум вдвое, так что общее число шагов составляет не более <math>\log_2 n</math>. Отсюда следует и оценка сложности алгоритма.
 +
 
 +
== Программная реализация алгоритма ==
 
=== Особенности реализации последовательного алгоритма ===
 
=== Особенности реализации последовательного алгоритма ===
−
=== Описание локальности данных и вычислений ===
+
 
−
=== Возможные способы и особенности реализации параллельного алгоритма ===
+
=== Возможные способы и особенности параллельной реализации алгоритма ===
−
=== Масштабируемость алгоритма и его реализации ===
+
Программа, реализующая алгоритм Борувки, состоит из двух частей:
−
=== Динамические характеристики и эффективность реализации алгоритма ===
+
 
 +
1. части, отвечающей за общую координацию вычислений
 +
 
 +
2. части, отвечающей за параллельные вычисления на многоядерных CPU или GPU.
 +
 
 +
 
 +
Описанный выше последовательный алгоритм не может применяться в параллельной программе: в реализации <math>MERGE</math> результаты операций <math>FIND(u)</math> и <math>FIND(v)</math> могут постоянно меняться, что приведёт к race condition. Параллельный вариант алгоритма описан в статье.
 +
 
 +
1. Каждой вершине v соответствует запись <math>A[v] = { parent, rank }</math>. Изначально <math>A[v] := { v, 0 }</math>.
 +
 
 +
2. Вспомогательная операция <math>UPDATE(v, rank_v, u, rank_u)</math>:
 +
 
 +
old := A[v]
 +
 
 +
if old.parent != v or old.rank != rank_v then return false
 +
 
 +
new := { u, rank_u }
 +
 
 +
return CAS(A[v], old, new)
 +
 
 +
3. Операция <math>FIND(v)</math>:
 +
 
 +
    while v != A[v].parent do
 +
        u := A[v].parent
 +
        CAS(A[v].parent, u, A[u].parent)
 +
        v := A[u].parent
 +
    return v
 +
 
 +
4. Операция UNION(u, v):
 +
 
 +
    while true do
 +
        (u, v) := (FIND(u), FIND(v))
 +
        if u = v then return false
 +
        (rank_u, rank_v) := (A[u].rank, A[v].rank)
 +
        if (A[u].rank, u) > (A[v].rank, v) then
 +
            swap((u, rank_u), (v, rank_v))
 +
        if UPDATE(u, rank_u, v, rank_u) then
 +
            if rank_u = rank_v then
 +
                UPDATE(v, rank_v, v, rank_v + 1)
 +
            return true
 +
 
 +
Для описанной версии алгоритма гарантируется свойство wait-free. На практике может использоваться упрощённая версия без подсчёта рангов, обладающая более слабым свойством lock-free, но в ряде случаев выигрывающая по скорости.
 +
 
 +
=== Результаты прогонов ===
 
=== Выводы для классов архитектур ===
 
=== Выводы для классов архитектур ===
−
=== Существующие реализации алгоритма ===
 
−
 
−
* C++, MPI: [http://www.boost.org/libs/graph_parallel/doc/html/index.html Parallel Boost Graph Library]; функции <code>[http://www.boost.org/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#dense-boruvka-minimum-spanning-tree dense_boruvka_minimum_spanning_tree]</code>, <code>[http://www.boost.org/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#boruvka_then_merge boruvka_then_merge]</code>, <code>[http://www.boost.org/libs/graph_parallel/doc/html/dehne_gotz_min_spanning_tree.html#boruvka_mixed_merge boruvka_mixed_merge]</code> сочетают алгоритм Борувки и [[алгоритм Крускала]].
 
  
 
== Литература ==
 
== Литература ==
  
 
<references />
 
<references />
 +
 +
[[Категория:Статьи в работе]]
 +
 +
[[En:Boruvka's algorithm]]

Текущая версия на 13:52, 5 июля 2022


Алгоритм Борувки
Последовательный алгоритм
Последовательная сложность [math]O(|E|ln(|V|))[/math]
Объём входных данных [math]O(|V| + |E|)[/math]
Объём выходных данных [math]O(|V|)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]max O(ln(|V|)) [/math]
Ширина ярусно-параллельной формы [math]O(|E|)[/math]


1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Борувки[1][2] предназначен для решения задачи о построении минимального остовного дерева во взвешенном неориентированном графе. Алгоритм хорошо параллелизуется и является основой для распределённого алгоритма GHS.

1.2 Математическое описание алгоритма

Пусть задан связный неориентированный граф [math]G = (V, E)[/math] с весами рёбер [math]f(e)[/math]. Предполагается, что веса всех рёбер различны (если это не так, то можно упорядочить рёбра сначала по весу, а потом по номеру).

Алгоритм Борувки основан на следующих двух свойствах задачи:

  • Минимальное ребро фрагмента. Пусть [math]F[/math] – фрагмент минимального остовного дерева и [math]e_F[/math] – ребро наименьшего веса, исходящее из [math]F[/math] (т.е. ровно один его конец является вершиной из [math]F[/math]). Если ребро [math]e_F[/math] единственно, то оно принадлежит минимальному остовному дереву.
  • Схлопывание фрагментов. Пусть [math]F[/math] – фрагмент минимального остовного дерева графа [math]G[/math], а граф [math]G'[/math] получен из [math]G[/math] склеиванием вершин, принадлежащих [math]F[/math]. Тогда объединение [math]F[/math] и минимального остовного дерева графа [math]G'[/math] даёт минимальное остовное дерево исходного графа [math]G[/math].

В начале работы алгоритма каждая вершина графа [math]G[/math] является отдельным фрагментом. На очередном шаге у каждого фрагмента выбирается исходящее ребро минимального веса (если такое ребро существует). Выбранные рёбра добавляются в минимальное остовное дерево, а соответствующие фрагменты склеиваются.

1.3 Вычислительное ядро алгоритма

Основными операциями являются:

  1. Поиск минимального по весу исходящего ребра в каждом фрагменте.
  2. Объединение фрагментов.

1.4 Макроструктура алгоритма

В задаче требуется указать в данном связном взвешенном графе дерево, соединяющее все его вершины и имеющее наименьший возможный суммарный вес рёбер.

Классический пример (из статьи Борувки) – спроектировать наиболее дешёвую электрическую сеть, зная стоимость устройства каждого участка электрической линии.

Пусть задан связный граф [math]G=(V,E)[/math] с вершинами [math]V = ( v_{1}, v_{2}, ..., v_{n} )[/math] и рёбрами [math]E = ( e_{1}, e_{2}, ..., e_{m} )[/math]. Каждому ребру [math]e \in E[/math] приписан вес [math]w(e)[/math].

Требуется построить дерево [math]T^* \subseteq E[/math], связывающее все вершины и имеющее наименьший возможный вес среди всех таких деревьев:

[math] w(T^* )= \min_T( w(T)) [/math]

где вес множества рёбер есть сумма их весов:

[math]w(T)=\sum_{e \in T} (w(T))[/math]

Если граф [math]G[/math] не является связным, то дерева, связывающего все вершины, не существует.

В этом случае необходимо найти минимальной остовное дерево для каждой компоненты связности [math]G[/math]. Набор таких деревьев называется минимальным остовным лесом (сокращённо MSF – Minimum Spanning Forest).

1.4.1 Вспомогательный алгоритм: система непересекающихся множеств (Union-Find)

Во всех алгоритмах решения задачи требуется отслеживать, каким уже построенным фрагментам дерева принадлежат те или иные вершины графа. Для этого используется структура данных «система непересекающихся множеств» (Union-Find). Данная структура поддерживает две операции:

1. [math]FIND(v) = w[/math] – по вершине v возвращает вершину w – «корень» фрагмента, которому принадлежит вершина v. При этом гарантируется, что вершины u и v принадлежат одному и тому же фрагменту, тогда и только тогда, когда [math]FIND(u) = FIND(v)[/math].

2. [math]MERGE(u, v)[/math] – объединяет два фрагмента, которым принадлежат вершины [math]u[/math] и [math]v.[/math] (Если они уже лежат в одном фрагменте, то ничего не происходит.) При практической реализации удобно, чтобы данная операция возвращала значение истина, если объединение фрагментов имело место, и ложь в противном случае.

1.4.2 Последовательная версия

Классический последовательный алгоритм Union-Find описан в статье Тарьяна. Каждой вершине v приписывается указатель на вершину-родителя [math]parent(v)[/math].

1. Изначально [math]parent(v) := v[/math] для всех вершин.

2. [math]FIND(v)[/math] выполняется следующим образом: полагаем [math]u := v[/math], и далее следуем по указателям [math]u := parent(u)[/math] до тех пор, пока не станет [math]u = parent(u)[/math]. Это и будет результат операции. Дополнительно можно «схлопывать» дерево: присвоить всем посещённым вершинами: [math]parent(u_i) := u[/math], либо производить схлопывание по пути: [math]parent(u) := parent(parent(u)))[/math].

3. [math]MERGE(u, v)[/math] выполняется следующим образом: вначале находим корневые вершины [math]u := FIND(u), v := FIND(v)[/math]. Если [math]u = v[/math], то исходные вершины принадлежат одному фрагменту и объединения фрагментов не происходит. В противном случае полагаем одно из [math]parent(u) := v[/math] или [math]parent(v) := u[/math]. Дополнительно можно отслеживать количество вершин в каждом из фрагментов, чтобы меньший фрагмент подсоединять к большему, а не наоборот (оценки сложности доказываются именно при такой реализации, однако на практике алгоритм хорошо работает и без подсчёта количества вершин).

1.5 Схема реализации последовательного алгоритма

В алгоритме Борувки фрагменты минимального остовного дерева наращиваются постепенно присоединением минимального ребра, выходящего из каждого фрагмента.

1. В самом начале каждая вершина является отдельным фрагментом.

2. На каждом шаге:

  • Для каждого фрагмента определяется минимальное по весу исходящее ребро.
  • Минимальные рёбра добавляются в минимальное остовное дерево, а соответствующие фрагменты объединяются.

3. Алгоритм останавливается, когда остаётся только один фрагмент либо когда ни у одного из фрагментов нет исходящих рёбер.

Поиск минимальных исходящих рёбер может выполняться независимо для каждого фрагмента. Таким образом, данную стадию вычислений можно эффективно параллелизовать (в том числе с использованием массового параллелизма графических ускорителей).

Объединение фрагментов также может быть реализовано параллельно с использованием параллельной версии описанного выше алгоритма Union-Find.

Аккуратный подсчёт количества активных фрагментов позволяет остановить алгоритм Борувки на один шаг раньше обычного:

1. В начале итерации счётчик активных фрагментов обнуляется.

2. На этапе поиска минимальных рёбер счётчик увеличивается на единицу для каждого фрагмента, у которого были исходящие рёбра.

3. На этапе объединения фрагментов счётчик уменьшается на единицу каждый раз, когда операция [math]MERGE(u, v)[/math] вернула значение истина.

Если в конце итерации счётчик равен 0 или 1, то вычисления останавливаются. Параллелизм возможен на этапе сортировки рёбер по весу, однако основной ход алгоритма является последовательным.

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма Борувки для графа с [math]|V|[/math] вершинами и [math]|E|[/math] рёбрами составляет [math]O(|E| \ln(|V|))[/math] операций.

1.7 Информационный граф

В описанном подходе существует два уровня параллелизма: параллелизм в классическом алгоритме Борувки (нижний) и параллелизм в алгоритме обработки графа, не помещающегося в память.

Нижний уровень параллелизма: поиск минимальных исходящих рёбер может выполняться независимо для каждого фрагмента, благодаря чему данную стадию вычислений можно эффективно параллелизовать (как на GPU, так и на CPU). Объединение фрагментов также может быть реализовано параллельно с использованием описанного выше алгоритма Union-Find.

Верхний уровень параллелизма: построение отдельных минимальных основных деревьев для каждого из списков ребер может производиться параллельно. Например, список ребер может разбиваться на две части, одна из которых обрабатывается на GPU, а вторая параллельно на CPU.

Рисунок 1. Информационный граф нижнего уровня параллелизма

Рассмотрим информационные графы и подробное описание каждого из них. Также можно считать, что на рисунке 1 представлен информационный граф классического алгоритма Борувки, а на рисунке 2 — алгоритма обработки графа.

Нижний уровень параллелизма на графе алгоритма (рисунок 1) расположен на уровнях {3, 4, 5}, соответствующих операциям параллельного поиска минимальных исходящих ребер, а также на уровнях {6, 7, 8}, соответствующих операциям параллельного объединения деревьев. Также различные операции копирования {1, 2, 8, 9} выполняются параллельно. После выполнения тела цикла производится проверка {12} того, сколько деревьев осталось на текущем шаге, и если данное число не изменилось, то происходит выход из цикла, иначе переход к следующей итерации.

Верхний уровень параллелизма (рисунок 2), как уже говорилось, заключается в параллельном вычислении минимального остовного дерева (compute mst) для различных частей графа. Перед этим производится процесс инициализации (init process), данные которого используют последующие параллельные операции compute mst. Затем, после параллельных вычислений mst, происходит вычисление итогового основного дерева, после чего полученный результат сохраняется (save results).

Рисунок 2. Информационный граф верхнего уровня параллелизма

1.8 Ресурс параллелизма алгоритма

Итак, алгоритм Борувки обладает двумя уровнями параллелизма.

На верхнем уровне минимальные остовные деревья могут искаться для отдельных частей списка ребер графа (параллельные compute_MST на рисунке 2). Однако затем должно последовать финальное объединение полученных ребер и вычисление минимального остовного дерева для полученного графа, которое будет производиться последовательно.

Кроме того, вычисление каждого из минимальных остовных деревьев (параллельные compute_MST на рисунке 2) обладает внутренним ресурсом параллелизма, описанным далее. Операции инициализации и копирования данных ([1], [2], [9] на рисунке 1) могут производиться параллельно за [math]O(|V|)[/math] операций. Также параллельно могут производиться операции поиска минимальных исходящих ребер ([3],[4],[5]), при этом для каждой дуги и обратной к ней независимо, что даёт [math]2*O(|E|)[/math] параллельных операций. Помимо этого, операции объединения деревьев [6], [7], [8] могут также производиться параллельно за [math]O(|V|)[/math] операций.

В результате для классического алгоритма Борувки ширина ярусно-параллельной формы равна [math]O(|E|)[/math], а высота ЯПФ зависит от числа шагов алгоритма и ограничена сверху [math]O(ln(|V|))[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: взвешенный граф [math](V, E, W)[/math] ([math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] с весами [math]f_j[/math]).

Объём входных данных: [math]O(|V| + |E|)[/math].

Выходные данные: список рёбер минимального остовного дерева (для несвязного графа – список минимальных остовных деревьев для всех компонент связности).

Объём выходных данных: [math]O(|V|)[/math].

1.10 Свойства алгоритма

  1. Алгоритм останавливается за конечное число шагов, поскольку на каждом шаге становится по крайней мере на один фрагмент меньше.
  2. Более того, число фрагментов на каждом шаге уменьшается как минимум вдвое, так что общее число шагов составляет не более [math]\log_2 n[/math]. Отсюда следует и оценка сложности алгоритма.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Возможные способы и особенности параллельной реализации алгоритма

Программа, реализующая алгоритм Борувки, состоит из двух частей:

1. части, отвечающей за общую координацию вычислений

2. части, отвечающей за параллельные вычисления на многоядерных CPU или GPU.


Описанный выше последовательный алгоритм не может применяться в параллельной программе: в реализации [math]MERGE[/math] результаты операций [math]FIND(u)[/math] и [math]FIND(v)[/math] могут постоянно меняться, что приведёт к race condition. Параллельный вариант алгоритма описан в статье.

1. Каждой вершине v соответствует запись [math]A[v] = { parent, rank }[/math]. Изначально [math]A[v] := { v, 0 }[/math].

2. Вспомогательная операция [math]UPDATE(v, rank_v, u, rank_u)[/math]:

old := A[v]

if old.parent != v or old.rank != rank_v then return false

new := { u, rank_u }

return CAS(A[v], old, new)

3. Операция [math]FIND(v)[/math]: 

   while v != A[v].parent do
       u := A[v].parent
       CAS(A[v].parent, u, A[u].parent)
       v := A[u].parent
   return v

4. Операция UNION(u, v): 

   while true do
       (u, v) := (FIND(u), FIND(v))
       if u = v then return false
       (rank_u, rank_v) := (A[u].rank, A[v].rank)
       if (A[u].rank, u) > (A[v].rank, v) then
           swap((u, rank_u), (v, rank_v))
       if UPDATE(u, rank_u, v, rank_u) then
           if rank_u = rank_v then
               UPDATE(v, rank_v, v, rank_v + 1)
           return true

Для описанной версии алгоритма гарантируется свойство wait-free. На практике может использоваться упрощённая версия без подсчёта рангов, обладающая более слабым свойством lock-free, но в ряде случаев выигрывающая по скорости.

2.3 Результаты прогонов

2.4 Выводы для классов архитектур

3 Литература

  1. ↑ Borůvka, Otakar. “O Jistém Problému Minimálním.” Práce Moravské Přírodovědecké Společnosti III, no. 3 (1926): 37–58.
  2. ↑ Jarník, Vojtěch. “O Jistém Problému Minimálním (Z Dopisu Panu O. Borůvkovi).” Práce Moravské Přírodovědecké Společnosti 6, no. 4 (1930): 57–63.
Источник — https://algowiki-project.org/w/ru/index.php?title=Алгоритм_Борувки&oldid=28956