Нахождение частных сумм элементов массива сдваиванием: различия между версиями
| [выверенная версия] | [досмотренная версия] |
Frolov (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 16 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
Основные авторы описания: [[Участник:Frolov|А.В.Фролов]] | Основные авторы описания: [[Участник:Frolov|А.В.Фролов]] | ||
| + | |||
| + | {{level-a}} | ||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 5: | Строка 7: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | '''Метод сдваивания''' используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового получения частичных сумм). Получил распространение благодаря наименьшей из возможных высоте алгоритма. | + | '''Метод сдваивания'''<ref>Фролов А.В. Использование последовательно-параллельного метода для распараллеливания алгоритмов с ассоциативными операциями // Принята в качестве доклада на первую объединенную международную конференцию "Суперкомпьютерные дни в России", Москва, 28-29 сентября 2015 г.</ref> используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового получения частичных сумм). Получил распространение благодаря наименьшей из возможных высоте алгоритма. Данный алгоритм (нахождение частных сумм элементов массива сдваиванием) является только наиболее простой моделью для показа свойств алгоритма сдваивания. |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 15: | Строка 17: | ||
Формулы метода: элементы на первом этапе алгоритма разбиваются на пары. В каждой из пар находится сумма составляющих её соседних элементов. | Формулы метода: элементы на первом этапе алгоритма разбиваются на пары. В каждой из пар находится сумма составляющих её соседних элементов. | ||
На следующем этапе на пары разбиваются уже эти суммы (и те элементы, которые не вошли в уже вычисленные суммы), и т. д. | На следующем этапе на пары разбиваются уже эти суммы (и те элементы, которые не вошли в уже вычисленные суммы), и т. д. | ||
| − | По нахождению тех частных сумм, где <math>i</math> является степенью двойки, формулы повторяют [[Нахождение суммы элементов массива сдваиванием]]. | + | По нахождению тех частных сумм, где <math>i</math> является степенью двойки, формулы повторяют [[Нахождение суммы элементов массива сдваиванием|алгоритм нахождения суммы элементов массива сдваиванием]]. |
Однако, кроме этого, для каждой пары (например, для нахождения суммы <math>x_i+...+x_{i+k}</math> и <math>x_{i+k+1} +...+ x_{i+2k}</math>)дополнительно вычисляются все частные суммы от <math>x_i+...+x_{i+k+1}</math> до <math>x_i+...+x_{i+2k-1}</math>. | Однако, кроме этого, для каждой пары (например, для нахождения суммы <math>x_i+...+x_{i+k}</math> и <math>x_{i+k+1} +...+ x_{i+2k}</math>)дополнительно вычисляются все частные суммы от <math>x_i+...+x_{i+k+1}</math> до <math>x_i+...+x_{i+2k-1}</math>. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | Вычислительное ядро | + | Вычислительное ядро метода сдваивания суммирования можно составить из элементарных бинарных (всего <math>\frac{n}{2} log_2 n</math>) вычислений сумм. |
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| Строка 35: | Строка 37: | ||
=== Информационный граф === | === Информационный граф === | ||
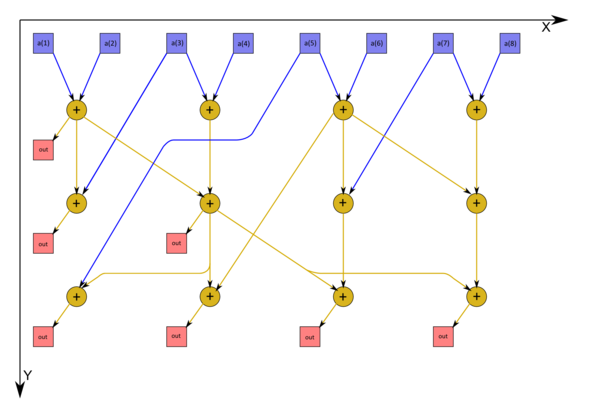
| − | [[File:DoublingPartUniv.png|thumb| | + | [[File:DoublingPartUniv.png|thumb|center|600px|Рисунок 1. Граф алгоритма при n=8 c отображением входных данных. Синим обозначены входные, красным - выходные данные. Все вершины соответствуют операции сложения]] |
Граф алгоритма изображён на рисунке. | Граф алгоритма изображён на рисунке. | ||
| Строка 58: | Строка 60: | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является <math>\frac{n}{2}</math> (отношение линейно-логарифмической к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — логарифмическая | + | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является <math>\frac{n}{2}</math> (отношение линейно-логарифмической к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — логарифмическая <math>\frac{1}{2} log_2 n</math>. Это, однако, обусловлено избыточностью вычислений, реальная мощность - константа (1). При этом алгоритм полностью детерминирован. Дуги информационного графа нелокальны, от яруса к ярусу наблюдается показательный рост их длины, при любом размещении вершин графа (кроме дополнительных измерений в случае расположения вершин в гиперкубе). |
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| Строка 66: | Строка 68: | ||
Сдваивание, из-за сильной избыточности вычислений, вряд ли может быть применено на компьютерах без параллельных устройств. | Сдваивание, из-за сильной избыточности вычислений, вряд ли может быть применено на компьютерах без параллельных устройств. | ||
| − | |||
| − | |||
| − | |||
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | + | ||
| − | + | Ввиду малораспространённости задачи нахождения частных сумм в библиотеках программ данный алгоритм обычно не содержится. | |
| − | + | ||
| − | === | + | Как видно по графу алгоритма, ряд дуг длинны как по времени (по различию номеров ярусов операций, являющихся началом и концом дуги), так и по пространству (исключением является только размещение в гиперкубе, физически невозможное). Эта неустранимая нелокальность должна тормозить исполнение всех аналогичных алгоритмов. |
| + | |||
| + | При оценке масштабируемости этого алгоритма, как и всех алгоритмов с избыточными вычислениями, следует учитывать, что сравнение по быстродействию и эффективности нужно проводить не с однопроцессорным вариантом исполнения самого алгоритма, а с алгоритмом последовательного сложения чисел. | ||
| + | |||
| + | === Результаты прогонов === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
Из-за своеобразия графа сдваивания лучше всего он отображается на архитектуру типа "гиперкуб". Поэтому для архитектур с массовым параллелизмом представляется неизбежным рост накладных расходов и слабая масштабируемость алгоритма. | Из-за своеобразия графа сдваивания лучше всего он отображается на архитектуру типа "гиперкуб". Поэтому для архитектур с массовым параллелизмом представляется неизбежным рост накладных расходов и слабая масштабируемость алгоритма. | ||
| − | == | + | == Литература == |
| − | |||
<references /> | <references /> | ||
| − | [[Категория: | + | [[Категория:Законченные_статьи]] |
[[Категория:Метод сдваивания]] | [[Категория:Метод сдваивания]] | ||
[[Категория:Алгоритмы с избыточными вычислениями]] | [[Категория:Алгоритмы с избыточными вычислениями]] | ||
| + | [[Категория:Векторные операции]] | ||
| + | |||
| + | [[en:Parallel prefix scan algorithm using pairwise summation]] | ||
Текущая версия на 12:58, 8 июля 2022
Основные авторы описания: А.В.Фролов
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод сдваивания[1] используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового получения частичных сумм). Получил распространение благодаря наименьшей из возможных высоте алгоритма. Данный алгоритм (нахождение частных сумм элементов массива сдваиванием) является только наиболее простой моделью для показа свойств алгоритма сдваивания.
1.2 Математическое описание алгоритма
Исходные данные: одномерный массив [math]n[/math] чисел.
Вычисляемые данные: частичные суммы первых [math]i[/math] элементов массива, где [math]i[/math] принимает все значения от [math]1[/math] до [math]n[/math].
Формулы метода: элементы на первом этапе алгоритма разбиваются на пары. В каждой из пар находится сумма составляющих её соседних элементов. На следующем этапе на пары разбиваются уже эти суммы (и те элементы, которые не вошли в уже вычисленные суммы), и т. д. По нахождению тех частных сумм, где [math]i[/math] является степенью двойки, формулы повторяют алгоритм нахождения суммы элементов массива сдваиванием. Однако, кроме этого, для каждой пары (например, для нахождения суммы [math]x_i+...+x_{i+k}[/math] и [math]x_{i+k+1} +...+ x_{i+2k}[/math])дополнительно вычисляются все частные суммы от [math]x_i+...+x_{i+k+1}[/math] до [math]x_i+...+x_{i+2k-1}[/math].
1.3 Вычислительное ядро алгоритма
Вычислительное ядро метода сдваивания суммирования можно составить из элементарных бинарных (всего [math]\frac{n}{2} log_2 n[/math]) вычислений сумм.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть метода составляют элементарные бинарные (всего [math]\frac{n}{2} log_2 n[/math]) вычисления сумм.
1.5 Схема реализации последовательного алгоритма
В описанном виде суммирование сдваиванием не используют при последовательной реализации, поскольку кроме усложнения общей схемы алгоритма и резкого роста потребности в памяти, нужной для хранения промежуточных данных, сам по себе алгоритм содержит подавляющее большинство избыточных вычислений: по сравнению с последовательным алгоритмом нахождения частных сумм количество операций больше в [math]\frac{1}{2} log_2 n[/math] раз.
1.6 Последовательная сложность алгоритма
Для вычисления суммы массива, состоящего из [math]n[/math] элементов, количество операций равно [math]\frac{n}{2} log_2 n[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейно-логарифмической сложности по количеству последовательных операций.
1.7 Информационный граф
Граф алгоритма изображён на рисунке.
1.8 Ресурс параллелизма алгоритма
Для вычисления частичных сумм массива порядка [math]n[/math] методом сдваивания в параллельном варианте требуется последовательно выполнить [math]\lceil \log_2 n \rceil[/math] ярусов с одинаковым ([math]\frac{n}{2}[/math]) количеством операций суммирования. При классификации по высоте ЯПФ, таким образом, метод сдваивания относится к алгоритмам с логарифмической сложностью. При классификации по ширине ЯПФ его сложность будет линейной.
1.9 Входные и выходные данные алгоритма
Входные данные: массив [math]x[/math] (элементы [math]x_i[/math]).
Дополнительные ограничения: отсутствуют.
Объём входных данных: [math]n[/math].
Выходные данные: все частичные суммы первых [math]i[/math] элементов массива, где [math]i[/math] принимает все значения от [math]1[/math] до [math]n[/math].
Объём выходных данных: [math]n[/math].
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является [math]\frac{n}{2}[/math] (отношение линейно-логарифмической к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — логарифмическая [math]\frac{1}{2} log_2 n[/math]. Это, однако, обусловлено избыточностью вычислений, реальная мощность - константа (1). При этом алгоритм полностью детерминирован. Дуги информационного графа нелокальны, от яруса к ярусу наблюдается показательный рост их длины, при любом размещении вершин графа (кроме дополнительных измерений в случае расположения вершин в гиперкубе).
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Сдваивание, из-за сильной избыточности вычислений, вряд ли может быть применено на компьютерах без параллельных устройств.
2.2 Возможные способы и особенности параллельной реализации алгоритма
Ввиду малораспространённости задачи нахождения частных сумм в библиотеках программ данный алгоритм обычно не содержится.
Как видно по графу алгоритма, ряд дуг длинны как по времени (по различию номеров ярусов операций, являющихся началом и концом дуги), так и по пространству (исключением является только размещение в гиперкубе, физически невозможное). Эта неустранимая нелокальность должна тормозить исполнение всех аналогичных алгоритмов.
При оценке масштабируемости этого алгоритма, как и всех алгоритмов с избыточными вычислениями, следует учитывать, что сравнение по быстродействию и эффективности нужно проводить не с однопроцессорным вариантом исполнения самого алгоритма, а с алгоритмом последовательного сложения чисел.
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
Из-за своеобразия графа сдваивания лучше всего он отображается на архитектуру типа "гиперкуб". Поэтому для архитектур с массовым параллелизмом представляется неизбежным рост накладных расходов и слабая масштабируемость алгоритма.
3 Литература
- ↑ Фролов А.В. Использование последовательно-параллельного метода для распараллеливания алгоритмов с ассоциативными операциями // Принята в качестве доклада на первую объединенную международную конференцию "Суперкомпьютерные дни в России", Москва, 28-29 сентября 2015 г.