Последовательно-параллельный метод суммирования: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
Frolov (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 36 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{level-a}} | |
| − | + | Основные авторы описания: [[Участник:Frolov|А.В.Фролов]]. | |
| − | + | == Свойства и структура алгоритма == | |
| − | === Математическое описание === | + | === Общее описание алгоритма === |
| + | |||
| + | '''Последовательно-параллельный метод''' используется в качестве эрзаца блочной реализации вычисления длинных последовательностей ассоциативных операций (например, массового суммирования). Получил распространение благодаря следующим особенностям: а) реализует приём получения двойных циклов из одинарных; б) в последовательной архитектуре компьютеров позволял для ряда операций уменьшать влияние округления на результат. Здесь будем описывать его версию для суммирования чисел. | ||
| + | |||
| + | === Математическое описание алгоритма === | ||
Исходные данные: одномерный массив <math>N</math> чисел. | Исходные данные: одномерный массив <math>N</math> чисел. | ||
| Строка 36: | Строка 40: | ||
:<math>\sum_{i = 1}^p S_i</math> | :<math>\sum_{i = 1}^p S_i</math> | ||
| − | === | + | === Схема реализации последовательного алгоритма === |
Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов). | Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов). | ||
| Строка 46: | Строка 50: | ||
=== Информационный граф === | === Информационный граф === | ||
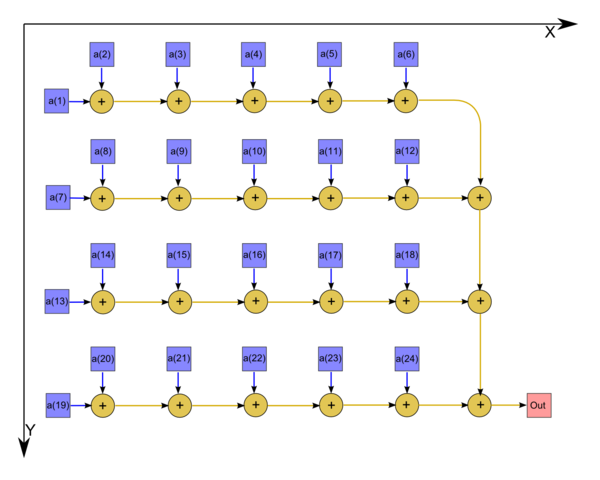
| − | + | На рис.1 изображён граф алгоритма. В данном случае выполнено суммирование 24 элементов массива. | |
| + | |||
| + | [[file:series-parallel summation graph.png|center|thumb|600px|Рисунок 1. Последовательно-параллельный метод суммирования массива]] | ||
| − | + | <center> | |
| + | {{#widget:Algoviewer | ||
| + | |url=seq_par/Algo_view_seq_par4.html | ||
| + | |width=1300 | ||
| + | |height=800 | ||
| + | |border=1 | ||
| + | }} | ||
| + | <br/> | ||
| + | Интерактивное изображение графа алгоритма без входных и выходных данных для случая суммирования 20 элементов массива | ||
| + | </center> | ||
=== Описание ресурса параллелизма алгоритма === | === Описание ресурса параллелизма алгоритма === | ||
| Строка 60: | Строка 75: | ||
При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью ''корень квадратный''. При классификации по ширине ЯПФ его сложность будет такой же — ''корень квадратный''. | При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью ''корень квадратный''. При классификации по ширине ЯПФ его сложность будет такой же — ''корень квадратный''. | ||
| − | === | + | === Входные и выходные данные алгоритма === |
Входные данные: массив <math>\vec{x}</math> (элементы <math>x_i</math>). | Входные данные: массив <math>\vec{x}</math> (элементы <math>x_i</math>). | ||
| Строка 76: | Строка 91: | ||
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является ''корнем квадратным'' (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего ''1 (входных и выходных данных столько же, сколько операций)''. При этом алгоритм не вполне полностью детерминирован, суммирование может быть проведено в разном порядке. Использование другого порядка выполнения ассоциативных операций может дать, с учётом особенностей входных данных, уменьшение влияния ошибок округления на результат. Дуги информационного графа локальны. | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является ''корнем квадратным'' (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего ''1 (входных и выходных данных столько же, сколько операций)''. При этом алгоритм не вполне полностью детерминирован, суммирование может быть проведено в разном порядке. Использование другого порядка выполнения ассоциативных операций может дать, с учётом особенностей входных данных, уменьшение влияния ошибок округления на результат. Дуги информационного графа локальны. | ||
| − | == Программная реализация == | + | == Программная реализация алгоритма == |
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| Строка 102: | Строка 117: | ||
Можно записать и аналогичные схемы, где суммирование будет проводиться в обратном порядке. Подчеркнём, что граф алгоритма обеих схем — [[#Информационный граф|один и тот же]]! | Можно записать и аналогичные схемы, где суммирование будет проводиться в обратном порядке. Подчеркнём, что граф алгоритма обеих схем — [[#Информационный граф|один и тот же]]! | ||
| − | === | + | === Возможные способы и особенности параллельной реализации алгоритма === |
| − | |||
| − | |||
| − | |||
| − | + | В чистом виде алгоритм последовательно-параллельного метода для суммирования массива встречается редко, в основном встречаются его модификации, например для случаев вычисления скалярного произведения (вместо элементов массива будут фигурировать произведения элементов двух массивов), равномерной нормы (вместо элементов массива — их модули) и т. п. В случае вычисления скалярного произведения в одном из частных случаев подобный приём применён в библиотеке BLAS (там одна из размерностей равна 5), но, видимо, не для распараллеливания, а для оптимизации работы с регистрами процессора. Между тем, разбиения массивов на группы для вычислений частных сумм могут быть полезны и для лучшего использования кэша на отдельных узлах. | |
| − | + | === Результаты прогонов === | |
| − | + | === Выводы для классов архитектур === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ===== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Литература == | |
| − | + | <references /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Категория:Законченные статьи]] | |
| − | + | [[Категория:Последовательно-параллельная группировка операций]] | |
| − | + | [[Категория:Векторные операции]] | |
| − | + | [[En:The serial-parallel summation method]] | |
Текущая версия на 15:10, 8 июля 2022
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Последовательно-параллельный метод используется в качестве эрзаца блочной реализации вычисления длинных последовательностей ассоциативных операций (например, массового суммирования). Получил распространение благодаря следующим особенностям: а) реализует приём получения двойных циклов из одинарных; б) в последовательной архитектуре компьютеров позволял для ряда операций уменьшать влияние округления на результат. Здесь будем описывать его версию для суммирования чисел.
1.2 Математическое описание алгоритма
Исходные данные: одномерный массив [math]N[/math] чисел.
Вычисляемые данные: сумма элементов массива.
Формулы метода: число [math]N[/math] разлагается в выражение типа [math]N = (p - 1) k + q[/math], где [math]p[/math] — количество процессоров, [math]k = \lceil \frac{N}{p} \rceil[/math], [math]q = N - k (p - 1)[/math].
После этого на [math]i[/math]-м процессоре ([math]i \lt p[/math]) последовательно вычисляется сумма элементов массива, начиная с [math](i - 1) k + 1[/math]-го, до [math]i k[/math]-го.
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
На [math]p[/math]-м процессоре последовательно вычисляется сумма элементов массива, начиная с [math](p - 1) k + 1[/math]-го до [math](p - 1) k + q[/math]-го.
- [math]S_p = \sum_{j = 1}^q x_{k (p - 1) + j}[/math]
По окончании этого процесса процессоры обмениваются данными и на одном из них (либо на всех одновременно, если результат нужен далее на всех процессорах) получившиеся суммы суммируются последовательно друг с другом.
- [math]\sum_{i = 1}^p S_i[/math]
1.3 Вычислительное ядро алгоритма
Вычислительное ядро последовательно-параллельного метода суммирования можно составить из множественных (всего [math]p[/math]) вычислений сумм элементов массива:
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
и ещё одного вычисления суммы элементов частичных сумм
- [math]\sum_{i = 1}^p S_i[/math]
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть метода составляют множественные (всего [math]p + 1[/math]) вычисления сумм
- [math]S_i = \sum_{j = 1}^k x_{k (i - 1) + j}[/math]
- [math]\sum_{i = 1}^p S_i[/math]
1.5 Схема реализации последовательного алгоритма
Формулы метода описаны выше. Последовательность исполнения суммирования может быть разная — как по возрастанию, так и по убыванию индексов. Обычно без особых причин порядок не меняют, используя естественный (возрастание индексов).
1.6 Последовательная сложность алгоритма
Для вычисления суммы массива, состоящего из [math]N[/math] элементов, при любых разложениях [math]N[/math] суть алгоритма сводится к простому переставлению скобок в формуле суммирования, и количество операций неизменно и равно [math]N - 1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.
1.7 Информационный граф
На рис.1 изображён граф алгоритма. В данном случае выполнено суммирование 24 элементов массива.
Интерактивное изображение графа алгоритма без входных и выходных данных для случая суммирования 20 элементов массива
1.8 Описание ресурса параллелизма алгоритма
Для суммирования массива порядка [math]n[/math] последовательно-параллельным методом в параллельном варианте требуется последовательно выполнить следующие ярусы:
- [math]k - 1[/math] ярусов суммирования по частям массива ([math]p[/math] ветвей),
- [math]p - 1[/math] ярусов суммирования (одна последовательная ветвь).
Таким образом, в параллельном варианте критический путь алгоритма (и соответствующая ему высота ЯПФ) будет зависеть от произведённого разбиения массива на части. В оптимальном случае ([math]p = \sqrt{n}[/math]) высота ЯПФ будет равна [math]2 \sqrt{n} - 2[/math].
При классификации по высоте ЯПФ, таким образом, последовательно-параллельный метод относится к алгоритмам со сложностью корень квадратный. При классификации по ширине ЯПФ его сложность будет такой же — корень квадратный.
1.9 Входные и выходные данные алгоритма
Входные данные: массив [math]\vec{x}[/math] (элементы [math]x_i[/math]).
Дополнительные ограничения: отсутствуют.
Объём входных данных: [math]N[/math].
Выходные данные: сумма элементов массива.
Объём выходных данных: один скаляр.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является корнем квадратным (отношение линейной к корню квадратному). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных столько же, сколько операций). При этом алгоритм не вполне полностью детерминирован, суммирование может быть проведено в разном порядке. Использование другого порядка выполнения ассоциативных операций может дать, с учётом особенностей входных данных, уменьшение влияния ошибок округления на результат. Дуги информационного графа локальны.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В простейшем (без перестановок суммирования) варианте на Фортране можно записать так:
DO I = 1, P
S (I) = X(K*(I-1)+1)
IF (I.LQ.P) THEN
DO J = 2,K
S(I)=S(I)+X(K*(I-1)+J)
END DO
ELSE
DO J = 2,Q
S(I)=S(I)+X(K*(I-1)+J)
END DO
END IF
END DO
SUM = S(1)
DO I = 2, P
SUM = SUM + S(I)
END DO
Можно записать и аналогичные схемы, где суммирование будет проводиться в обратном порядке. Подчеркнём, что граф алгоритма обеих схем — один и тот же!
2.2 Возможные способы и особенности параллельной реализации алгоритма
В чистом виде алгоритм последовательно-параллельного метода для суммирования массива встречается редко, в основном встречаются его модификации, например для случаев вычисления скалярного произведения (вместо элементов массива будут фигурировать произведения элементов двух массивов), равномерной нормы (вместо элементов массива — их модули) и т. п. В случае вычисления скалярного произведения в одном из частных случаев подобный приём применён в библиотеке BLAS (там одна из размерностей равна 5), но, видимо, не для распараллеливания, а для оптимизации работы с регистрами процессора. Между тем, разбиения массивов на группы для вычислений частных сумм могут быть полезны и для лучшего использования кэша на отдельных узлах.