Linpack benchmark: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
ASA (обсуждение | вклад) |
|||
| (не показаны 42 промежуточные версии 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{level-a}} | |
| − | + | Основные авторы описания: [[Участник:Frolov|А.В.Фролов]]. | |
| − | '''Linpack benchmark''' является тестом, разработанным как приложение к библиотеке Linpack для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) <math>A \vec{x} = \vec{b}</math> со случайной плотной квадратной матрицей <math>A</math> и вектором <math>\vec{b}</math> таким, чтобы решением был вектор <math>\vec{x}</math>, у которого все элементы равны 1, с последующим решением этой СЛАУ. Решение в силу неспецифичности (с рядом оговорок) матрицы делается в | + | == Свойства и структура алгоритма == |
| + | |||
| + | === Общее описание алгоритма === | ||
| + | |||
| + | '''Linpack benchmark''' является тестом, разработанным как приложение к библиотеке Linpack для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) <math>A \vec{x} = \vec{b}</math> со случайной плотной квадратной матрицей <math>A</math> и вектором <math>\vec{b}</math> таким, чтобы решением был вектор <math>\vec{x}</math>, у которого все элементы равны 1, с последующим решением этой СЛАУ. Решение в силу неспецифичности (с рядом оговорок) матрицы делается в несколько этапов. Сначала для матрицы системы выполняется <math>PLU</math>-разложение (<math>P</math> — матрица перестановок, <math>L</math> — левая треугольная с единичными диагональными элементами, <math>U</math> — правая треугольная матрица) методом Гаусса с выбором ведущего элемента по столбцу. На втором этапе с помощью полученного разложения последовательно решается СЛАУ вида <math>P L U \vec{x} = \vec{b}</math>. На третьем этапе вычисляется невязка <math>\vec{r} = A \vec{x} - \vec{b}</math> и её характеристики, после чего выводятся данные о полученных точности и производительности вычислений. Интересно, что производительность вычисляется только для основной части алгоритма, т. е. туда не включены ни вычисление невязки, ни вычисление норм. | ||
Не следует путать Linpack benchmark, разработанный для тестирования компьютеров традиционной архитектуры, и High Performance Linpack benchmark, который разработан для тестирования компьютерных систем с параллельной архитектурой и в основе которого лежит хоть и сходный, но другой алгоритм. | Не следует путать Linpack benchmark, разработанный для тестирования компьютеров традиционной архитектуры, и High Performance Linpack benchmark, который разработан для тестирования компьютерных систем с параллельной архитектурой и в основе которого лежит хоть и сходный, но другой алгоритм. | ||
| − | === Математическое описание === | + | === Математическое описание алгоритма === |
Исходные данные: невырожденная (ГСЧ подобран так, чтобы это обеспечивалось, в версии от 1992 г.) квадратная матрица <math>A</math> (элементы <math>a_{ij}</math>), вектор правой части <math>\vec{b}</math> (элементы <math>b_i</math>). В реальности они не вполне входные (элементы матрицы генерирует псевдослучайно сама программа, все они находятся в диапазоне (-1/2, +1/2), <math>b_i = \sum\limits_{j = 1}^i a_{ij}</math>), но для разбора общей схемы алгоритма удобно считать их входными данными. | Исходные данные: невырожденная (ГСЧ подобран так, чтобы это обеспечивалось, в версии от 1992 г.) квадратная матрица <math>A</math> (элементы <math>a_{ij}</math>), вектор правой части <math>\vec{b}</math> (элементы <math>b_i</math>). В реальности они не вполне входные (элементы матрицы генерирует псевдослучайно сама программа, все они находятся в диапазоне (-1/2, +1/2), <math>b_i = \sum\limits_{j = 1}^i a_{ij}</math>), но для разбора общей схемы алгоритма удобно считать их входными данными. | ||
| Строка 17: | Строка 21: | ||
Первая часть — разложение матрицы в произведение двух треугольных и матрицы перестановок: <math>A = P L U</math> — выполняется методом Гаусса с выбором ведущего элемента по столбцу. При этом матрица перестановок хранится с помощью вектора, характеризующего выполненные перестановки. Матрица <math>L</math> левая треугольная с единичными диагональными элементами, матрица <math>U</math> — правая треугольная. | Первая часть — разложение матрицы в произведение двух треугольных и матрицы перестановок: <math>A = P L U</math> — выполняется методом Гаусса с выбором ведущего элемента по столбцу. При этом матрица перестановок хранится с помощью вектора, характеризующего выполненные перестановки. Матрица <math>L</math> левая треугольная с единичными диагональными элементами, матрица <math>U</math> — правая треугольная. | ||
| − | Вторая часть состоит из двух решений треугольных СЛАУ. Сначала c помощью | + | Вторая часть состоит из двух решений треугольных СЛАУ. Сначала c помощью прямого хода решается система <math>L \vec{y} = P T \vec{b}</math>, затем с помощью обратной подстановки — система <math>U \vec{x} = \vec{y}</math>. При этом в тесте треугольные матрицы хранятся в соответствующих местах матрицы <math>A</math>. Поэтому перед началом третьей части её генерируют заново (с теми же стартовыми параметрами для ГСЧ). |
Третья часть (для которой не измеряется скорость работы) состоит в вычислении сначала невязки решения <math>\vec{r} = A \vec{x} - \vec{b}</math> и затем её равномерной нормы, а также нормы решения. По окончании этой части алгоритм выдаёт данные по точности полученного решения, а также вычисляет производительность системы. | Третья часть (для которой не измеряется скорость работы) состоит в вычислении сначала невязки решения <math>\vec{r} = A \vec{x} - \vec{b}</math> и затем её равномерной нормы, а также нормы решения. По окончании этой части алгоритм выдаёт данные по точности полученного решения, а также вычисляет производительность системы. | ||
| Строка 23: | Строка 27: | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | Основная часть алгоритма — разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций. Следующая по значимости часть — вычисление невязки и её нормы — реализовано подпрограммой вычисления суммы вектора и произведения матрицы на другой вектор и функцией вычисления равномерной нормы. Третьи по значимости части — | + | Основная часть алгоритма — разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций. Следующая по значимости часть — вычисление невязки и её нормы — реализовано подпрограммой вычисления суммы вектора и произведения матрицы на другой вектор и функцией вычисления равномерной нормы. Третьи по значимости части — прямой ход и обратная подстановка в методе Гаусса. |
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | Как уже записано в описании ядра алгоритма, разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций и при этом является первой макрооперацией. После неё идёт | + | Как уже записано в описании ядра алгоритма, разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций и при этом является первой макрооперацией. После неё идёт прямой ход метода Гаусса и сразу за ним обратная подстановка. После повторного заполнения матрицы следующей макрооперацией является вычисление невязки решения СЛАУ, а затем — вычисление её и вектора решения равномерных норм. |
| − | === | + | === Схема реализации последовательного алгоритма === |
| − | Математическое описание алгоритма | + | Математическое описание алгоритма дано выше. При этом в стандартном тесте из-за того, что разложение Гаусса вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. После вычисления невязки её норма в принципе может быть вычислена в любом порядке с нормой решения, это не влияет на алгоритм и его результаты. |
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 39: | Строка 43: | ||
=== Информационный граф === | === Информационный граф === | ||
| − | / | + | Граф состоит из информационных графов своих основных частей. Первая часть (метод Гаусса с выбором ведущего элемента по столбцу) имеет самый сложный из графов. На рис.1 отражён упрощённый граф этой части, post factum по результатам выборов ведущих элементов. Зеленым отображены операции определения максимумов, с запоминанием позиций. Желтым цветом выделено обращение очередного ведущего элемента, коричневым – умножения в текущем столбце, фиолетовым – операции <math>a b + c</math> в других столбцах. На рис.2 приведён граф одного из слоёв (одного шага метода). Обозначения – те же самые, что в полном графе. Пунктир означает рассылку данных из ведущей строки. |
| − | + | {| align="center" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| align=" | ||
|- valign="top" | |- valign="top" | ||
| − | | [[File:Gaussian elimination.png|700px|thumb]] | + | | [[File:Gaussian elimination.png|700px|thumb|Рисунок 1. Упрощённый граф метода Гаусса с выбором ведущего элемента по столбцу]] |
| − | | [[File:Gaussian elimination step.png|500px|thumb]] | + | | [[File:Gaussian elimination step.png|500px|Рисунок 2. Граф одного шага метода Гаусса|thumb]] |
|} | |} | ||
| − | Вторая часть состоит из почти аналогичных фрагментов. Первый из них – «прямой ход», а именно решение СЛАУ с левой треугольной матрицей <math>L \vec{y} = \vec{b}</math>. Диагональные элементы матрицы единичны, поэтому в этом куске нет операций деления. Все зелёные вершины отвечают операциям <math>a b + c</math>. Второй – «обратный ход», а именно решение СЛАУ с правой (верхней) треугольной матрицей <math>U \vec{x} = \vec{y}</math>. Для её матрицы нет информации о специфичности, и потому в графе появляются также операции деления. | + | Вторая часть состоит из почти аналогичных фрагментов. Первый из них – «прямой ход», а именно решение СЛАУ с левой треугольной матрицей <math>L \vec{y} = \vec{b}</math> (рис.3). Диагональные элементы матрицы единичны, поэтому в этом куске нет операций деления. Все зелёные вершины отвечают операциям <math>a b + c</math>. Второй – «обратный ход», а именно решение СЛАУ с правой (верхней) треугольной матрицей <math>U \vec{x} = \vec{y}</math> (рис.4). Для её матрицы нет информации о специфичности, и потому в графе появляются также операции деления , они обозначены желтым цветом. |
| − | {| align=" | + | {| align="center" |
|- valign="top" | |- valign="top" | ||
| − | | [[File: | + | | [[File:DirectL.png|500px|thumb|Рисунок 3. Граф решения СЛАУ с левой треугольной матрицей]] |
| − | | [[File: | + | | [[File:DirectU.png|450px|thumb|Рисунок 4. Граф решения СЛАУ с правой треугольной матрицей]] |
|} | |} | ||
| − | === | + | === Ресурс параллелизма алгоритма === |
| − | При изучении ресурса параллелизма теста видно, что основная сложность (''квадратичная'') будет у разложения Гаусса с выбором ведущего элемента по столбцу (именно из-за наличия выбора элемента по столбцу). Остальные части алгоритма имеют не более линейной сложности. Поэтому для оптимизации вычислений возможному исследователю нужно заняться именно оптимизацией разложения Гаусса с выбором ведущего элемента по столбцу. Кроме этого, первый кусок второй части (решение первой из треугольных СЛАУ) может быть пристыкован к первой части исполнен почти полностью «на её фоне», ибо направление перевычисления данных у них совпадают. Однако второй кусок второй части, несмотря на его схожесть с первым, может быть вычислен не ранее, чем будет выполнен весь первый кусок, поскольку у них направления перевычисления данных противоположны. | + | При изучении ресурса параллелизма теста видно, что основная сложность (''квадратичная'') будет у разложения Гаусса с выбором ведущего элемента по столбцу (именно из-за наличия выбора элемента по столбцу). Остальные части алгоритма имеют не более линейной сложности. Поэтому для оптимизации вычислений возможному исследователю нужно заняться именно оптимизацией разложения Гаусса с выбором ведущего элемента по столбцу. Кроме этого, первый кусок второй части (решение первой из треугольных СЛАУ) может быть пристыкован к первой части и исполнен почти полностью «на её фоне», ибо направление перевычисления данных у них совпадают. Однако второй кусок второй части, несмотря на его схожесть с первым, может быть вычислен не ранее, чем будет выполнен весь первый кусок, поскольку у них направления перевычисления данных противоположны. |
| − | === | + | === Входные и выходные данные алгоритма === |
По сути теста у него всегда одни и те же данные, причём вычисляемые в самом же тесте. Поэтому в строгом смысле у алгоритма нет входных данных. | По сути теста у него всегда одни и те же данные, причём вычисляемые в самом же тесте. Поэтому в строгом смысле у алгоритма нет входных данных. | ||
| Строка 75: | Строка 71: | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | == Программная реализация == | + | == Программная реализация алгоритма == |
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | Строго говоря, при реализации теста испытывающий компьютерную систему испытывает и версии Линпака или другого пакета, откуда он должен вставлять вызовы разложения | + | Строго говоря, при реализации теста испытывающий компьютерную систему испытывает и версии Линпака или другого пакета, откуда он должен вставлять вызовы треугольного разложения матрицы и решения СЛАУ с помощью полученного разложения. Поэтому находящиеся в сети версии теста не являются догмой, поскольку с их помощью можно тестировать и другие версии реализации метода Гаусса. Как уже отмечено выше, из-за того, что треугольное разложение вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. Это решение вполне можно поменять с целью оптимизации теста. |
| − | + | === Возможные способы и особенности параллельной реализации алгоритма === | |
| − | + | === Результаты прогонов === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | === Возможные способы и особенности | ||
| − | |||
| − | |||
| − | |||
| − | === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | == | + | |
| + | == Литература == | ||
| + | |||
| + | <references /> | ||
| + | |||
| + | [[Категория:Статьи в работе]] | ||
| + | [[Категория:Решение систем линейных уравнений]] | ||
| + | |||
| + | [[En:Linpack benchmark]] | ||
Текущая версия на 16:13, 12 июля 2022
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Linpack benchmark является тестом, разработанным как приложение к библиотеке Linpack для тестирования производительности компьютерных систем. По сути это генерирование некоторой системы линейных алгебраических уравнений (СЛАУ) [math]A \vec{x} = \vec{b}[/math] со случайной плотной квадратной матрицей [math]A[/math] и вектором [math]\vec{b}[/math] таким, чтобы решением был вектор [math]\vec{x}[/math], у которого все элементы равны 1, с последующим решением этой СЛАУ. Решение в силу неспецифичности (с рядом оговорок) матрицы делается в несколько этапов. Сначала для матрицы системы выполняется [math]PLU[/math]-разложение ([math]P[/math] — матрица перестановок, [math]L[/math] — левая треугольная с единичными диагональными элементами, [math]U[/math] — правая треугольная матрица) методом Гаусса с выбором ведущего элемента по столбцу. На втором этапе с помощью полученного разложения последовательно решается СЛАУ вида [math]P L U \vec{x} = \vec{b}[/math]. На третьем этапе вычисляется невязка [math]\vec{r} = A \vec{x} - \vec{b}[/math] и её характеристики, после чего выводятся данные о полученных точности и производительности вычислений. Интересно, что производительность вычисляется только для основной части алгоритма, т. е. туда не включены ни вычисление невязки, ни вычисление норм.
Не следует путать Linpack benchmark, разработанный для тестирования компьютеров традиционной архитектуры, и High Performance Linpack benchmark, который разработан для тестирования компьютерных систем с параллельной архитектурой и в основе которого лежит хоть и сходный, но другой алгоритм.
1.2 Математическое описание алгоритма
Исходные данные: невырожденная (ГСЧ подобран так, чтобы это обеспечивалось, в версии от 1992 г.) квадратная матрица [math]A[/math] (элементы [math]a_{ij}[/math]), вектор правой части [math]\vec{b}[/math] (элементы [math]b_i[/math]). В реальности они не вполне входные (элементы матрицы генерирует псевдослучайно сама программа, все они находятся в диапазоне (-1/2, +1/2), [math]b_i = \sum\limits_{j = 1}^i a_{ij}[/math]), но для разбора общей схемы алгоритма удобно считать их входными данными.
Вычисляемые данные: левая треугольная матрица [math]L[/math] (элементы [math]l_{ij}[/math]), правая треугольная матрица [math]U[/math] (элементы [math]u_{ij}[/math]), матрица перестановок [math]P[/math] (вычисляется не в развёрнутом виде, а как набор номеров ведущих элементов), вектор решения [math]x[/math] (элементы [math]x_i[/math]).
Детальные формулы отдельных частей алгоритма здесь описывать не будем, поскольку они являются самостоятельными алгоритмами и их детальные описания должны быть выполнены раздельно. Поэтому здесь будет приведена только общая схема алгоритма.
Первая часть — разложение матрицы в произведение двух треугольных и матрицы перестановок: [math]A = P L U[/math] — выполняется методом Гаусса с выбором ведущего элемента по столбцу. При этом матрица перестановок хранится с помощью вектора, характеризующего выполненные перестановки. Матрица [math]L[/math] левая треугольная с единичными диагональными элементами, матрица [math]U[/math] — правая треугольная.
Вторая часть состоит из двух решений треугольных СЛАУ. Сначала c помощью прямого хода решается система [math]L \vec{y} = P T \vec{b}[/math], затем с помощью обратной подстановки — система [math]U \vec{x} = \vec{y}[/math]. При этом в тесте треугольные матрицы хранятся в соответствующих местах матрицы [math]A[/math]. Поэтому перед началом третьей части её генерируют заново (с теми же стартовыми параметрами для ГСЧ).
Третья часть (для которой не измеряется скорость работы) состоит в вычислении сначала невязки решения [math]\vec{r} = A \vec{x} - \vec{b}[/math] и затем её равномерной нормы, а также нормы решения. По окончании этой части алгоритм выдаёт данные по точности полученного решения, а также вычисляет производительность системы.
1.3 Вычислительное ядро алгоритма
Основная часть алгоритма — разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций. Следующая по значимости часть — вычисление невязки и её нормы — реализовано подпрограммой вычисления суммы вектора и произведения матрицы на другой вектор и функцией вычисления равномерной нормы. Третьи по значимости части — прямой ход и обратная подстановка в методе Гаусса.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, разложение матрицы методом Гаусса с выбором ведущих элементов по столбцу — определяет основную часть операций и при этом является первой макрооперацией. После неё идёт прямой ход метода Гаусса и сразу за ним обратная подстановка. После повторного заполнения матрицы следующей макрооперацией является вычисление невязки решения СЛАУ, а затем — вычисление её и вектора решения равномерных норм.
1.5 Схема реализации последовательного алгоритма
Математическое описание алгоритма дано выше. При этом в стандартном тесте из-за того, что разложение Гаусса вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. После вычисления невязки её норма в принципе может быть вычислена в любом порядке с нормой решения, это не влияет на алгоритм и его результаты.
1.6 Последовательная сложность алгоритма
Поскольку основной частью алгоритма является разложение Гаусса с выбором ведущего элемента по столбцу, то он, как и эта часть, относится к алгоритмам с кубической сложностью. Остальные части квадратичны по сложности и потому не дают сравнимого вклада в сложность алгоритма.
1.7 Информационный граф
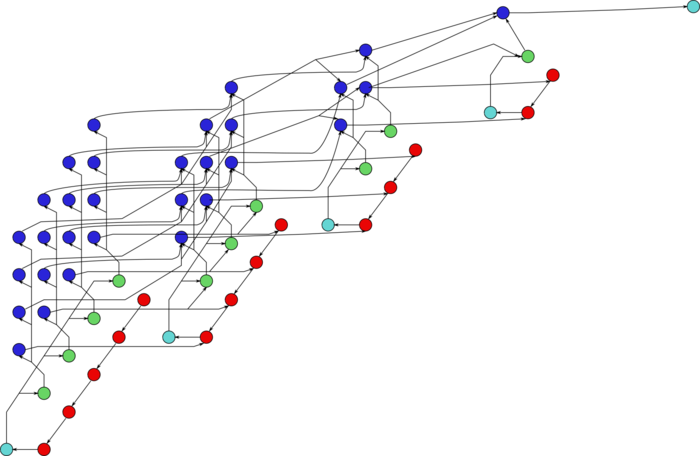
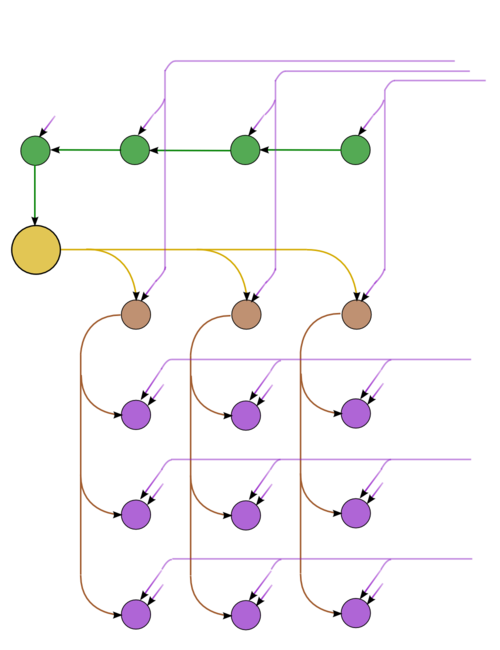
Граф состоит из информационных графов своих основных частей. Первая часть (метод Гаусса с выбором ведущего элемента по столбцу) имеет самый сложный из графов. На рис.1 отражён упрощённый граф этой части, post factum по результатам выборов ведущих элементов. Зеленым отображены операции определения максимумов, с запоминанием позиций. Желтым цветом выделено обращение очередного ведущего элемента, коричневым – умножения в текущем столбце, фиолетовым – операции [math]a b + c[/math] в других столбцах. На рис.2 приведён граф одного из слоёв (одного шага метода). Обозначения – те же самые, что в полном графе. Пунктир означает рассылку данных из ведущей строки.
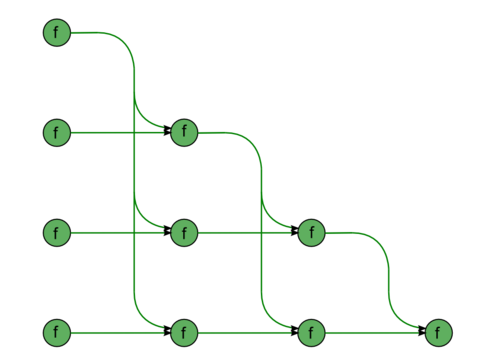
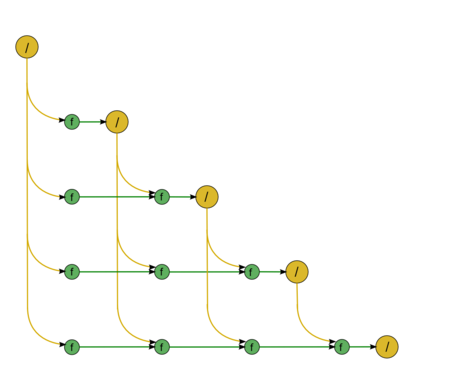
Вторая часть состоит из почти аналогичных фрагментов. Первый из них – «прямой ход», а именно решение СЛАУ с левой треугольной матрицей [math]L \vec{y} = \vec{b}[/math] (рис.3). Диагональные элементы матрицы единичны, поэтому в этом куске нет операций деления. Все зелёные вершины отвечают операциям [math]a b + c[/math]. Второй – «обратный ход», а именно решение СЛАУ с правой (верхней) треугольной матрицей [math]U \vec{x} = \vec{y}[/math] (рис.4). Для её матрицы нет информации о специфичности, и потому в графе появляются также операции деления , они обозначены желтым цветом.
1.8 Ресурс параллелизма алгоритма
При изучении ресурса параллелизма теста видно, что основная сложность (квадратичная) будет у разложения Гаусса с выбором ведущего элемента по столбцу (именно из-за наличия выбора элемента по столбцу). Остальные части алгоритма имеют не более линейной сложности. Поэтому для оптимизации вычислений возможному исследователю нужно заняться именно оптимизацией разложения Гаусса с выбором ведущего элемента по столбцу. Кроме этого, первый кусок второй части (решение первой из треугольных СЛАУ) может быть пристыкован к первой части и исполнен почти полностью «на её фоне», ибо направление перевычисления данных у них совпадают. Однако второй кусок второй части, несмотря на его схожесть с первым, может быть вычислен не ранее, чем будет выполнен весь первый кусок, поскольку у них направления перевычисления данных противоположны.
1.9 Входные и выходные данные алгоритма
По сути теста у него всегда одни и те же данные, причём вычисляемые в самом же тесте. Поэтому в строгом смысле у алгоритма нет входных данных.
Выходными данными являются вычисляемые и выдаваемые тестом нормы невязки, решения, матрицы и их отношения, а также вычисляемая мощность вычислений целевой вычислительной системы.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Строго говоря, при реализации теста испытывающий компьютерную систему испытывает и версии Линпака или другого пакета, откуда он должен вставлять вызовы треугольного разложения матрицы и решения СЛАУ с помощью полученного разложения. Поэтому находящиеся в сети версии теста не являются догмой, поскольку с их помощью можно тестировать и другие версии реализации метода Гаусса. Как уже отмечено выше, из-за того, что треугольное разложение вычисляется на месте исходной матрицы, а также из-за того, что при прямом и обратном ходе решение занимает место правой части, после вычисления решения приходится заново перевычислять как матрицу системы, так и правую часть — для последующего вычисления невязки. Это решение вполне можно поменять с целью оптимизации теста.