Участник:Popko Fedor/Параллельная реализация явной разностной схемы для решения уравнения теплопроводности: различия между версиями
| (не показано 15 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | [[Участник:Popko Fedor]] | ||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Явная разностная схема для решения уравнения теплопроводности с правой частью предназначена для моделирования процессов теплопередачи в материале с учётом внешнего источника тепла. Уравнение теплопроводности с правой частью имеет вид: | + | Явная разностная схема для решения уравнения теплопроводности с правой частью предназначена для моделирования процессов теплопередачи в материале с учётом внешнего источника тепла. Уравнение теплопроводности <ref>Тихонов А.Н., Самарский А.А. Уравнения математической физики.</ref> с правой частью имеет вид: |
<math>\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2} + f(x, t),</math> | <math>\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2} + f(x, t),</math> | ||
где <math>u(x, t)</math> — температура в точке <math>x</math> в момент времени <math>t</math>, <math>a</math> — коэффициент теплопроводности материала, <math>f(x, t)</math> — правая часть, описывающая внешний источник или сток тепла. | где <math>u(x, t)</math> — температура в точке <math>x</math> в момент времени <math>t</math>, <math>a</math> — коэффициент теплопроводности материала, <math>f(x, t)</math> — правая часть, описывающая внешний источник или сток тепла. | ||
| + | Также необходимо задать: | ||
| + | |||
| + | 1. '''Граничные условия''': | ||
| + | |||
| + | Граничные условия задаются на краях области <math>x = 0</math> и <math>x = L</math> и бывают нескольких типов. | ||
| + | |||
| + | * Граничные условия первого рода (условия Дирихле): | ||
| + | |||
| + | Граничные условия первого рода устанавливают фиксированные значения температуры на границах области, то есть она поддерживается постоянной и равной заранее заданной функции времени. | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | u(0, t) = u_{\text{left}}(t), \\ | ||
| + | u(L, t) = u_{\text{right}}(t), | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | где <math>u_{\text{left}}(t)</math> и <math>u_{\text{right}}(t)</math> — заданные значения температуры на левой и правой границах области. | ||
| + | |||
| + | * Граничные условия второго рода (условия Неймана): | ||
| + | |||
| + | Граничные условия второго рода определяют тепловой поток через границы области, то есть устанавливают значение производной температуры по нормали к поверхности. Это означает, что на границах тепловой поток поддерживается постоянным. | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | \frac{\partial u}{\partial x}\Big|_{x=0} = q_{\text{left}}(t), \\ | ||
| + | \frac{\partial u}{\partial x}\Big|_{x=L} = q_{\text{right}}(t), | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | где <math>q_{\text{left}}(t)</math> и <math>q_{\text{right}}(t)</math> — заданные значения теплового потока на левой и правой границах. | ||
| + | |||
| + | 2. '''Начальные условия''': | ||
| + | |||
| + | Задаются для всего стержня при начальном времени <math>t = 0</math>: | ||
| + | <math>u(x, 0) = u_0(x),</math> | ||
| + | где <math>u_0(x)</math> — начальное распределение температуры по всей длине стержня. | ||
| + | |||
| + | |||
| + | Далее будем рассматривать граничные условия первого рода равные нулю. | ||
| + | Тогда итоговая система будет иметь вид: | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | \frac{\partial u}{\partial t} = a \frac{\partial^2 u}{\partial x^2} + f(x, t), & 0 < x < L, \, t > 0, \\ | ||
| + | u(0, t) = u(L, t) = 0, \\ | ||
| + | u(x, 0) = u_0(x), & 0 \leq x \leq L . | ||
| + | \end{cases} | ||
| + | </math> | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| + | Для явной разностной схемы<ref> Самарский А.А. Теория разностных схем. — Москва: Наука, 1989.</ref> приближаем производные конечными разностями на каждом временном шаге, обновляя <math>u(x, t)</math> в каждой точке сетки по пространству, используя значения с предыдущего временного шага. Пусть <math>\Delta x</math> — шаг по пространству, а <math>\Delta t</math> — шаг по времени. | ||
| + | |||
| + | 1. '''Аппроксимация производной по пространству''': | ||
| + | |||
| + | Вторую производную по <math>x</math> можно аппроксимировать следующим образом: | ||
| + | <math>\frac{\partial^2 u}{\partial x^2} \approx \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2},</math> | ||
| + | где <math>u_i^n</math> — значение температуры в узле <math>i</math> на временном слое <math>n</math>. | ||
| + | |||
| + | 2. '''Аппроксимация производной по времени''': | ||
| + | |||
| + | Первую производную по <math>t</math> можно аппроксимировать так: | ||
| + | <math>\frac{\partial u}{\partial t} \approx \frac{u_i^{n+1} - u_i^n}{\Delta t}.</math> | ||
| + | |||
| + | 3. '''Схема явного метода''': | ||
| + | |||
| + | Подставляем аппроксимации производных в исходное уравнение теплопроводности: | ||
| + | <math>\frac{u_i^{n+1} - u_i^n}{\Delta t} = a \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2} + f(x_i, t_n).</math> | ||
| + | Теперь выразим <math>u_i^{n+1}</math>: | ||
| + | <math>u_i^{n+1} - u_i^n = \Delta t \cdot \left( a \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2} + f(x_i, t_n) \right).</math> | ||
| + | |||
| + | <math>u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2} + f(x_i, t_n) \right).</math> | ||
| + | |||
| + | Получилось явное выражение для <math>u_i^{n+1}</math>, которое позволяет вычислить температуру в узле <math>i</math> на следующем временном слое, используя значения с текущего временного слоя <math>n</math>. | ||
| + | |||
| + | |||
| + | 4. '''Граничные условия''': | ||
| + | |||
| + | Устанавливаем граничные условия для расчёта на краях области, в зависимости от физической постановки задачи, например, <math>u(0, t) = 0</math> и <math>u(L, t) =0</math> для закрепленных концов стержня. | ||
| + | |||
| + | 5. '''Начальные условия''': | ||
| + | |||
| + | Начальные условия для температуры по всему стержню <math>u(x, 0) = u_0(x)</math> для начального распределения температуры. | ||
| + | |||
| + | В результате, итоговая система уравнений для каждого временного слоя <math>n+1</math> и каждого узла <math>i</math> в сетке может быть записана как: | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^n - 2 u_i^n + u_{i-1}^n}{(\Delta x)^2} + f(x_i, t_n) \right), i = 1, \dots, L-1, \\ | ||
| + | u_0^{n+1} = u_L^{n+1} = 0, \\ | ||
| + | u_i^0 = u_0(x_i), i = 0, \dots, L. | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | 6. '''Устойчивость схемы ''' | ||
| + | |||
| + | Для явной разностной схемы, описывающей решение уравнения теплопроводности, важно учитывать условие устойчивости, которое определяет, при каких параметрах схемы решение будет сходиться. | ||
| + | Основное условие устойчивости для явной схемы: | ||
| + | |||
| + | <math> | ||
| + | \frac{a \Delta t}{(\Delta x)^2} \leq \frac{1}{2}, | ||
| + | </math> | ||
| + | где: <math>a</math> — коэффициент теплопроводности материала, <math>\Delta t</math> — шаг по времени, <math>\Delta x</math> — шаг по пространству. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| + | Вычислительное ядро алгоритма состоит в обновлении значений температуры в каждой точке сетки на каждом временном шаге согласно явной разностной схеме. Основная вычислительная операция заключается в вычислении новой температуры: | ||
| + | |||
| + | <math> | ||
| + | u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^n - 2 u_i^n + u_{i-1}^n}{(\Delta x)^2} + f(x_i, t_n) \right), \quad i = 1, \dots, L-1 | ||
| + | </math> | ||
| + | |||
| + | Это обновление выполняется для каждой внутренней точки сетки на каждом временном шаге. | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| + | # '''Инициализация''': На этом этапе задаются все входные параметры: коэффициент теплопроводности <math>a</math>, шаги по пространству и времени <math>\Delta x</math>, <math>\Delta t</math>, длина стержня <math>L</math>, общее время моделирования <math>T</math>, а также начальные и граничные условия. Этот этап не требует параллелизации. | ||
| + | # '''Основной цикл по времени''': Для каждого временного шага <math>n</math> вычисляются новые значения температуры для всех внутренних точек стержня. Каждый временной слой обрабатывается отдельно, и для каждой внутренней точки стержня вычисляется температура в следующем временном слое, а также происходит обновление граничных условий для новых значений <math>u_0^{n+1}</math>, <math>u_L^{n+1}</math>. | ||
| + | # '''Основной цикл по пространству''': На каждом временном шаге, для каждого узла <math>i</math>, выполняется вычисление новой температуры по следующей формуле: <math>u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^n - 2 u_i^n + u_{i-1}^n}{(\Delta x)^2} + f(x_i, t_n) \right)</math>. Этап является параллельным, так как каждое вычисление для узла <math>i</math> зависит только от значений на предыдущем временном шаге, что позволяет выполнять вычисления независимо для каждого узла на одном временном шаге. | ||
| + | |||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| + | Последовательный алгоритм реализуется в виде вложенных циклов: | ||
| + | |||
| + | * Цикл по времени: Для каждого временного шага выполняется обновление температур в пространстве. | ||
| + | * Цикл по пространству: Обновление значений <math>u_i^{n+1}</math> для всех внутренних точек сетки. | ||
| + | |||
| + | <pre> | ||
| + | Инициализация параметров и массивов; | ||
| + | |||
| + | Для n от 0 до N_t - 1: | ||
| + | Для i от 1 до N_x - 1: | ||
| + | u_new[i] = u_old[i] + Δt * (a * (u_old[i+1] - 2*u_old[i] + u_old[i-1]) / (Δx)^2 + f(x_i, t_n)); | ||
| + | Конец цикла по i; | ||
| + | |||
| + | Применение граничных условий для u_new; | ||
| + | |||
| + | u_old = u_new; | ||
| + | |||
| + | Конец цикла по n; | ||
| + | </pre> | ||
| + | |||
| + | |||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | Для каждого временного шага необходимо обновить значения температуры во всех внутренних точках сетки. Если сетка содержит <math>N_x</math> пространственных узлов, то на каждом временном шаге требуется выполнить <math>N_x-2</math> обновлений (исключая граничные узлы). Общее число арифметических операций на один временной шаг пропорционально <math>\mathcal{O}(N_x)</math>. | ||
| + | Для всех временных шагов общее количество операций составляет: <math>\mathcal{O}(N_t \cdot N_x)</math>, где <math>N_t</math> — общее количество временных шагов. | ||
=== Информационный граф === | === Информационный граф === | ||
| + | Вершины графа соответствуют операциям вычисления температуры в узлах сетки, обозначаемым координатами <math>(n,i)</math>, где <math>n</math> — временной слой, <math>i</math> — пространственный узел. | ||
| + | Дуги графа отражают информационные зависимости между операциями. Дуга из узла <math>(n−1,j)</math> к узлу <math>(n,i)</math> указывает на то, что для вычисления <math>u_i^n</math> требуется значение <math>u_j^{n-1}</math> . | ||
| + | Так как вычисление каждого узла на временном слое <math>n</math> зависит только от значений узлов предыдущего слоя <math>n−1</math>, все операции внутри одного временного слоя могут выполняться независимо друг от друга. | ||
| + | [[Файл:Output.png|300px|thumb|center|Рис.1. Информационная структура]] | ||
| + | |||
| + | [[Файл:Шаблон явной схемы для уравнения теплопроводности..png|300px|thumb|center|Рис.2. Шаблон явной схемы для уравнения теплопроводности.]] | ||
| + | <br> | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | Параллельная сложность явной разностной схемы для уравнения теплопроводности определяется числом временных слоёв <math>N_t</math>,так как узлы каждого слоя могут вычисляться параллельно. Каждый временной слой зависит только от значений предыдущего слоя, на каждом ярусе ярусно-параллельной формы выполняются одинаковые операции (сложение, вычитание, умножение) с шириной яруса, равной <math>N_x</math> | ||
| + | === Входные и выходные данные алгоритма === | ||
| + | # Входные данные: Параметры задачи: коэффициент теплопроводности <math>a</math>, длина стержня <math>L</math>, общее время моделирования <math>T</math>. Начальные условия: функция <math>u_0(x)</math>, задающая начальное распределение температуры. Правая часть: функция <math>f(x,t)</math>, описывающая внешний источник тепла. Параметры сетки: шаг по пространству <math>\Delta x</math>, шаг по времени <math>\Delta t</math>. Общий объём входных данных (все параметры представлены как ''double''): <math>V_{\text{input}} = 8 \times (3 + 2 + N_x) \, \text{байт}.</math> | ||
| − | + | # Выходные данные: распределение температуры <math>u(x,t)</math> в узлах сетки для каждого временного шага или для выбранных моментов времени. Общий объём выходных данных: <math>V_{\text{output}} = N_x \times N_t \times 8 \, \text{байт}.</math> | |
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | Масштабируемость алгоритма решения уравнения теплопроводности с использованием явной разностной схемы зависит от нескольких факторов. Один из них разделение пространства на блоки, которые обрабатываются параллельно: чем больше блоков данных на процесс, тем меньше потерь на взаимодействие между процессами. Обмен граничными значениями между соседними процессами является основной проблемой<ref>Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, № 7, С. 36-39. | ||
| + | </ref> и для хорошей производительности необходимо минимизировать количество обменов. При увеличении числа узлов на процесс потери на обмены уменьшаются. Эффективность масштабируемости зависит от размеров задачи: при увеличении числа узлов и временных шагов объём вычислений растёт пропорционально. Для небольших задач накладные расходы на синхронизацию могут привести к снижению эффективности. | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | Существует множество последовательных реализаций алгоритма<ref>Разностные методы решения задач теплопроводности: учебное | ||
| + | пособие. / Г.В. Кузнецов, М.А. Шеремет. – Томск: Изд-во ТПУ, | ||
| + | 2007.</ref>, где вычисления выполняются на одном процессоре, что позволяет легко реализовать алгоритм и использовать его для небольших задач, однако его производительность ограничена. Для больших задач последовательный подход становится неэффективным, так как время выполнения растет. | ||
| + | Для решения крупных задач применяются параллельные реализации, распределяющие вычисления между несколькими процессами, например: | ||
| + | * Реализиция явной разностной схемы с использованием Tensorflow<ref>https://habr.com/ru/articles/321734/</ref>, позволяющем использовать GPU для вычислений. | ||
| + | * Реализация с использованием OpenMP<ref>https://github.com/UoB-HPC/openmp-tutorial/blob/master/Solutions/heat_data_reg.c</ref>, которая использует возможности многопоточности для распараллеливания вычислений на многоядерных процессорах. | ||
== Литература == | == Литература == | ||
Текущая версия на 14:03, 10 декабря 2024
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Явная разностная схема для решения уравнения теплопроводности с правой частью предназначена для моделирования процессов теплопередачи в материале с учётом внешнего источника тепла. Уравнение теплопроводности [1] с правой частью имеет вид:
[math]\frac{\partial u}{\partial t} = a\frac{\partial^2 u}{\partial x^2} + f(x, t),[/math]
где [math]u(x, t)[/math] — температура в точке [math]x[/math] в момент времени [math]t[/math], [math]a[/math] — коэффициент теплопроводности материала, [math]f(x, t)[/math] — правая часть, описывающая внешний источник или сток тепла. Также необходимо задать:
1. Граничные условия:
Граничные условия задаются на краях области [math]x = 0[/math] и [math]x = L[/math] и бывают нескольких типов.
- Граничные условия первого рода (условия Дирихле):
Граничные условия первого рода устанавливают фиксированные значения температуры на границах области, то есть она поддерживается постоянной и равной заранее заданной функции времени.
[math] \begin{cases} u(0, t) = u_{\text{left}}(t), \\ u(L, t) = u_{\text{right}}(t), \end{cases} [/math]
где [math]u_{\text{left}}(t)[/math] и [math]u_{\text{right}}(t)[/math] — заданные значения температуры на левой и правой границах области.
- Граничные условия второго рода (условия Неймана):
Граничные условия второго рода определяют тепловой поток через границы области, то есть устанавливают значение производной температуры по нормали к поверхности. Это означает, что на границах тепловой поток поддерживается постоянным.
[math] \begin{cases} \frac{\partial u}{\partial x}\Big|_{x=0} = q_{\text{left}}(t), \\ \frac{\partial u}{\partial x}\Big|_{x=L} = q_{\text{right}}(t), \end{cases} [/math]
где [math]q_{\text{left}}(t)[/math] и [math]q_{\text{right}}(t)[/math] — заданные значения теплового потока на левой и правой границах.
2. Начальные условия:
Задаются для всего стержня при начальном времени [math]t = 0[/math]: [math]u(x, 0) = u_0(x),[/math] где [math]u_0(x)[/math] — начальное распределение температуры по всей длине стержня.
Далее будем рассматривать граничные условия первого рода равные нулю.
Тогда итоговая система будет иметь вид:
[math] \begin{cases} \frac{\partial u}{\partial t} = a \frac{\partial^2 u}{\partial x^2} + f(x, t), & 0 \lt x \lt L, \, t \gt 0, \\ u(0, t) = u(L, t) = 0, \\ u(x, 0) = u_0(x), & 0 \leq x \leq L . \end{cases} [/math]
1.2 Математическое описание алгоритма
Для явной разностной схемы[2] приближаем производные конечными разностями на каждом временном шаге, обновляя [math]u(x, t)[/math] в каждой точке сетки по пространству, используя значения с предыдущего временного шага. Пусть [math]\Delta x[/math] — шаг по пространству, а [math]\Delta t[/math] — шаг по времени.
1. Аппроксимация производной по пространству:
Вторую производную по [math]x[/math] можно аппроксимировать следующим образом: [math]\frac{\partial^2 u}{\partial x^2} \approx \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2},[/math] где [math]u_i^n[/math] — значение температуры в узле [math]i[/math] на временном слое [math]n[/math].
2. Аппроксимация производной по времени:
Первую производную по [math]t[/math] можно аппроксимировать так: [math]\frac{\partial u}{\partial t} \approx \frac{u_i^{n+1} - u_i^n}{\Delta t}.[/math]
3. Схема явного метода:
Подставляем аппроксимации производных в исходное уравнение теплопроводности:
[math]\frac{u_i^{n+1} - u_i^n}{\Delta t} = a \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2} + f(x_i, t_n).[/math]
Теперь выразим [math]u_i^{n+1}[/math]:
[math]u_i^{n+1} - u_i^n = \Delta t \cdot \left( a \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2} + f(x_i, t_n) \right).[/math]
[math]u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^{n} - 2 u_{i}^{n} + u_{i-1}^{n}}{(\Delta x)^2} + f(x_i, t_n) \right).[/math]
Получилось явное выражение для [math]u_i^{n+1}[/math], которое позволяет вычислить температуру в узле [math]i[/math] на следующем временном слое, используя значения с текущего временного слоя [math]n[/math].
4. Граничные условия:
Устанавливаем граничные условия для расчёта на краях области, в зависимости от физической постановки задачи, например, [math]u(0, t) = 0[/math] и [math]u(L, t) =0[/math] для закрепленных концов стержня.
5. Начальные условия:
Начальные условия для температуры по всему стержню [math]u(x, 0) = u_0(x)[/math] для начального распределения температуры.
В результате, итоговая система уравнений для каждого временного слоя [math]n+1[/math] и каждого узла [math]i[/math] в сетке может быть записана как:
[math] \begin{cases} u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^n - 2 u_i^n + u_{i-1}^n}{(\Delta x)^2} + f(x_i, t_n) \right), i = 1, \dots, L-1, \\ u_0^{n+1} = u_L^{n+1} = 0, \\ u_i^0 = u_0(x_i), i = 0, \dots, L. \end{cases} [/math]
6. Устойчивость схемы
Для явной разностной схемы, описывающей решение уравнения теплопроводности, важно учитывать условие устойчивости, которое определяет, при каких параметрах схемы решение будет сходиться. Основное условие устойчивости для явной схемы:
[math] \frac{a \Delta t}{(\Delta x)^2} \leq \frac{1}{2}, [/math] где: [math]a[/math] — коэффициент теплопроводности материала, [math]\Delta t[/math] — шаг по времени, [math]\Delta x[/math] — шаг по пространству.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит в обновлении значений температуры в каждой точке сетки на каждом временном шаге согласно явной разностной схеме. Основная вычислительная операция заключается в вычислении новой температуры:
[math] u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^n - 2 u_i^n + u_{i-1}^n}{(\Delta x)^2} + f(x_i, t_n) \right), \quad i = 1, \dots, L-1 [/math]
Это обновление выполняется для каждой внутренней точки сетки на каждом временном шаге.
1.4 Макроструктура алгоритма
- Инициализация: На этом этапе задаются все входные параметры: коэффициент теплопроводности [math]a[/math], шаги по пространству и времени [math]\Delta x[/math], [math]\Delta t[/math], длина стержня [math]L[/math], общее время моделирования [math]T[/math], а также начальные и граничные условия. Этот этап не требует параллелизации.
- Основной цикл по времени: Для каждого временного шага [math]n[/math] вычисляются новые значения температуры для всех внутренних точек стержня. Каждый временной слой обрабатывается отдельно, и для каждой внутренней точки стержня вычисляется температура в следующем временном слое, а также происходит обновление граничных условий для новых значений [math]u_0^{n+1}[/math], [math]u_L^{n+1}[/math].
- Основной цикл по пространству: На каждом временном шаге, для каждого узла [math]i[/math], выполняется вычисление новой температуры по следующей формуле: [math]u_i^{n+1} = u_i^n + \Delta t \cdot \left( a \frac{u_{i+1}^n - 2 u_i^n + u_{i-1}^n}{(\Delta x)^2} + f(x_i, t_n) \right)[/math]. Этап является параллельным, так как каждое вычисление для узла [math]i[/math] зависит только от значений на предыдущем временном шаге, что позволяет выполнять вычисления независимо для каждого узла на одном временном шаге.
1.5 Схема реализации последовательного алгоритма
Последовательный алгоритм реализуется в виде вложенных циклов:
- Цикл по времени: Для каждого временного шага выполняется обновление температур в пространстве.
- Цикл по пространству: Обновление значений [math]u_i^{n+1}[/math] для всех внутренних точек сетки.
Инициализация параметров и массивов;
Для n от 0 до N_t - 1:
Для i от 1 до N_x - 1:
u_new[i] = u_old[i] + Δt * (a * (u_old[i+1] - 2*u_old[i] + u_old[i-1]) / (Δx)^2 + f(x_i, t_n));
Конец цикла по i;
Применение граничных условий для u_new;
u_old = u_new;
Конец цикла по n;
1.6 Последовательная сложность алгоритма
Для каждого временного шага необходимо обновить значения температуры во всех внутренних точках сетки. Если сетка содержит [math]N_x[/math] пространственных узлов, то на каждом временном шаге требуется выполнить [math]N_x-2[/math] обновлений (исключая граничные узлы). Общее число арифметических операций на один временной шаг пропорционально [math]\mathcal{O}(N_x)[/math]. Для всех временных шагов общее количество операций составляет: [math]\mathcal{O}(N_t \cdot N_x)[/math], где [math]N_t[/math] — общее количество временных шагов.
1.7 Информационный граф
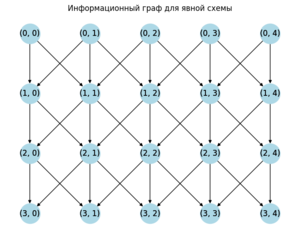
Вершины графа соответствуют операциям вычисления температуры в узлах сетки, обозначаемым координатами [math](n,i)[/math], где [math]n[/math] — временной слой, [math]i[/math] — пространственный узел. Дуги графа отражают информационные зависимости между операциями. Дуга из узла [math](n−1,j)[/math] к узлу [math](n,i)[/math] указывает на то, что для вычисления [math]u_i^n[/math] требуется значение [math]u_j^{n-1}[/math] . Так как вычисление каждого узла на временном слое [math]n[/math] зависит только от значений узлов предыдущего слоя [math]n−1[/math], все операции внутри одного временного слоя могут выполняться независимо друг от друга.
1.8 Ресурс параллелизма алгоритма
Параллельная сложность явной разностной схемы для уравнения теплопроводности определяется числом временных слоёв [math]N_t[/math],так как узлы каждого слоя могут вычисляться параллельно. Каждый временной слой зависит только от значений предыдущего слоя, на каждом ярусе ярусно-параллельной формы выполняются одинаковые операции (сложение, вычитание, умножение) с шириной яруса, равной [math]N_x[/math]
1.9 Входные и выходные данные алгоритма
- Входные данные: Параметры задачи: коэффициент теплопроводности [math]a[/math], длина стержня [math]L[/math], общее время моделирования [math]T[/math]. Начальные условия: функция [math]u_0(x)[/math], задающая начальное распределение температуры. Правая часть: функция [math]f(x,t)[/math], описывающая внешний источник тепла. Параметры сетки: шаг по пространству [math]\Delta x[/math], шаг по времени [math]\Delta t[/math]. Общий объём входных данных (все параметры представлены как double): [math]V_{\text{input}} = 8 \times (3 + 2 + N_x) \, \text{байт}.[/math]
- Выходные данные: распределение температуры [math]u(x,t)[/math] в узлах сетки для каждого временного шага или для выбранных моментов времени. Общий объём выходных данных: [math]V_{\text{output}} = N_x \times N_t \times 8 \, \text{байт}.[/math]
2 Программная реализация алгоритма
2.1 Масштабируемость алгоритма и его реализации
Масштабируемость алгоритма решения уравнения теплопроводности с использованием явной разностной схемы зависит от нескольких факторов. Один из них разделение пространства на блоки, которые обрабатываются параллельно: чем больше блоков данных на процесс, тем меньше потерь на взаимодействие между процессами. Обмен граничными значениями между соседними процессами является основной проблемой[3] и для хорошей производительности необходимо минимизировать количество обменов. При увеличении числа узлов на процесс потери на обмены уменьшаются. Эффективность масштабируемости зависит от размеров задачи: при увеличении числа узлов и временных шагов объём вычислений растёт пропорционально. Для небольших задач накладные расходы на синхронизацию могут привести к снижению эффективности.
2.2 Существующие реализации алгоритма
Существует множество последовательных реализаций алгоритма[4], где вычисления выполняются на одном процессоре, что позволяет легко реализовать алгоритм и использовать его для небольших задач, однако его производительность ограничена. Для больших задач последовательный подход становится неэффективным, так как время выполнения растет. Для решения крупных задач применяются параллельные реализации, распределяющие вычисления между несколькими процессами, например:
- Реализиция явной разностной схемы с использованием Tensorflow[5], позволяющем использовать GPU для вычислений.
- Реализация с использованием OpenMP[6], которая использует возможности многопоточности для распараллеливания вычислений на многоядерных процессорах.
3 Литература
- ↑ Тихонов А.Н., Самарский А.А. Уравнения математической физики.
- ↑ Самарский А.А. Теория разностных схем. — Москва: Наука, 1989.
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, № 7, С. 36-39.
- ↑ Разностные методы решения задач теплопроводности: учебное пособие. / Г.В. Кузнецов, М.А. Шеремет. – Томск: Изд-во ТПУ, 2007.
- ↑ https://habr.com/ru/articles/321734/
- ↑ https://github.com/UoB-HPC/openmp-tutorial/blob/master/Solutions/heat_data_reg.c