Алгоритм Качмажа: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
| Строка 97: | Строка 97: | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
| − | Алгоритм Качмажа, как любой итерационный алгоритм, является последовательным, в строковой версии алгоритма ресурс для параллелизма оказывается небольшим - только за счет параллельной реализации операции SAXPY. Однако, существуют различные блочные версии алгоритма Качмажа, где проектирование осуществляется не на конкретную гиперплоскость, а на их пересечение в рамках выбранного блока. Такие модификации имеют существенно больший ресурс для распараллеливания и связаны с трудоемкими задачами вычисления псевдообратной матрицы и задаче выбора оптимального размера блока (в общем случае не предполагается, что матрица разбивается на блоки равных размеров, что еще больше усложняет задачу). | + | Алгоритм Качмажа, как любой итерационный алгоритм, является последовательным, в строковой версии алгоритма ресурс для параллелизма оказывается небольшим - только за счет параллельной реализации операции SAXPY. |
| + | |||
| + | Однако, существуют различные блочные версии алгоритма Качмажа, где проектирование осуществляется не на конкретную гиперплоскость, а на их пересечение в рамках выбранного блока. Такие модификации имеют существенно больший ресурс для распараллеливания и связаны с трудоемкими задачами вычисления псевдообратной матрицы и задаче выбора оптимального размера блока (в общем случае не предполагается, что матрица разбивается на блоки равных размеров, что еще больше усложняет задачу). | ||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
Версия 15:11, 15 июля 2016
| Алгоритм Качмажа (S. Kaczmarz) |
Основные авторы описания: Е.С. Козлова, А.А. Иванов.
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 ЧАСТЬ. Дополнительная информация
- 4 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Стефан Качмаж (Stefan Kaczmarz) - польский математик, родился 1895 г. в городе Самбор (Sambor) Галиция (Galicia), Австро-Венгрия (Austria-Hungary), ныне Украина. Стефан Качмаж был профессором математики на факультете машиностроения университета Яна Казимира (Jan Kazimierz University) в городе Львов (Lwów) с 1919 по 1939 год, там же сотрудничал с Стефаном Банахом. Предложенный им итерационный метод решения с.л.а.у. послужил основой для многих современных технологий в обработке изображений, в том числе в задачах компьютерной томографии [1].
Применение метода С. Качмажа или т.н. метода алгебраической реконструкции наиболее известно в задачах реконструктивной компьютерной томографии высокого разрешения. Для интерпретации данных, полученных в результате неразрушающего сканирования некоторого объекта, с 60-70-х годов применяются различные аппаратные и программные реализации итерационного метода, разработанного польским математиком С. Качмажем (S. Kaczmarz) в 1937 году[2]; этот метод был использован Г. Хаусфилдом (G.N. Hounsfield) - конструктором первого томографа «ЭМИ-сканнер»[3] (нобелевская премия по физиологии и медицине в 1979 году).
Так же данный метод можно часто встретить под следующими названиями: Algebraic Reconstruction Technique (ART)[4][5][6], Projection onto Convex Sets (PCS)[7], Kaczmarz Algorithm [8] или метод ортогональных проекций.
Конструированию различных алгоритмов на основе итераций С. Качмажа посвящено существенное количество работ: согласно исследованию польского математика и библиографа А. Сигелски (A. Cegielski), на начало 2010 года статья С. Качмажа цитируется более чем в четырехстах реферируемых и значимых публикациях ученых из различных областей знаний. В Советской и Российской научных школах исследования итераций С. Качмажа представлены в литературе такими известными учеными как: В.Н. Ильин, Г.П. Васильченко, А.А. Светлаков и другие, например, в работах[9][10]. Общие идеи о проекционных методах так же представлены в классической работе Л. Г. Гурина, Б. Т. Поляка, Э. В. Райка[11], где впервые предлагается и обосновывается идентичный алгоритм для решения систем линейных алгебраических неравенств и уравнений.
В 2008 году американскими математиками Т. Штромером (T. Strohmer) и Р. Вершининым (R. Vershynin) в [12] была предложена рандомизированная модификация итерационного метода, в которой последовательность приближений к решению для совместных и переопределенных с.л.а.у. сходится с экспоненциальной скоростью.
Множество модификаций идеи метода ортогональных проекций нашли свое практическое применение в различных областях знаний, связанных с обработкой и интерпретацией больших объемов данных: при реконструкции синограмм в медицине, биологии, геологии; при решении задач диагностики плазмы, кристаллографии[13], дефектоскопии и микроскопии, параллельных вычислений и распределенного анализа[14] и др.
1.2 Математическое описание алгоритма
1.2.1 Математическое описание
Запишем совместную (в общем случае - переопределенную) с.л.а.у.
[math]Au=f,\, A\in R^{m\times n},\, u\in R^{n},\, f\in R^{m},[/math]
тогда итерации согласно алгоритму определяются последовательностью
[math]u^{k+1}=u^{k}+\lambda_{k}\frac{f_{j\left(k\right)}-\left(a_{j\left(k\right)},u^{k}\right)}{\Vert a_{j\left(k\right)}\Vert^{2}}a_{j\left(k\right)},[/math]
где
[math]A=\left(a_{1},\, a_{2},\,\ldots\,,\, a_{m}\right)^{T}\in R^{m\times n},\, u\in R^{n},\, f=\left(f_{1},\, f_{2},\,\ldots\,,\, f_{m}\right)\in R^{m},[/math]
а последовательность проектирования в классическом варианте алгоритма определяется как
[math]j\left(k\right)=\left(k\ \bmod\ m\right)+1,\, k=\overline{0,\infty},[/math]
где [math]k[/math] - номер итерации, [math]u^{0}[/math] - начальное приближение, а [math]\lambda_{k}[/math] - параметр релаксации (Рис. 2 построен для случая, когда [math]\lambda_{k}=1,\,\forall k[/math]).
1.2.2 Геометрическая интерпретация
Метод алгебраической реконструкции достаточно просто формулируется с использованием его геометрической интерпретации. Рассмотрим совместную с.л.а.у. с двумя неизвестными
[math]A=\begin{pmatrix}3 & 2\\
2 & 3
\end{pmatrix},\text{ }f=\begin{pmatrix}1\\
2
\end{pmatrix}[/math]
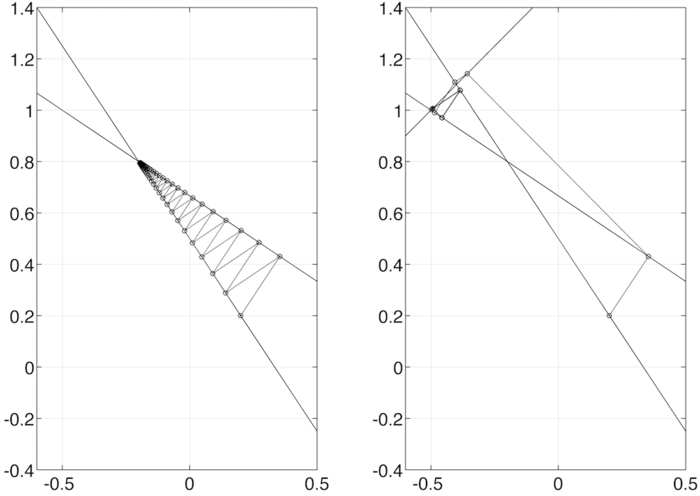
и несовместную переопределенную, полученную добавлением к этой системе дополнительного уравнения [math]-u_{1}+u_{2}=1.5[/math]. Каждое уравнение из с.л.а.у. можно интерпретировать как гиперплоскость в пространстве координат, а решение совместной с.л.а.у. - как точку пересечения всех этих гиперплоскостей. При использовании метода алгебраической реконструкции для решения с.л.а.у. поиск приближенного решения осуществляется в направлениях, перпендикулярных к гиперплоскостям, каждая из которых описывается отдельным уравнением решаемой системы (см. Рис.1).
Интерактивная диаграмма для совместного случая подготовлена авторами статьи здесь (Notes about S. Kaczmarz algorithm - consistent case), а для несовместного случая здесь (Notes about S. Kaczmarz algorithm - inconsistent case). Данные диаграммы позволяют регулировать параметры с.л.а.у. и начальное приближение, что позволяет наглядно демонстрировать сходимость итерационной последовательности.
Описанные результаты наводят на очевидную идею - проекционная последовательность влияет на скорость сходимости метода ортогональных проекций. Обратите внимание на Рис.2.
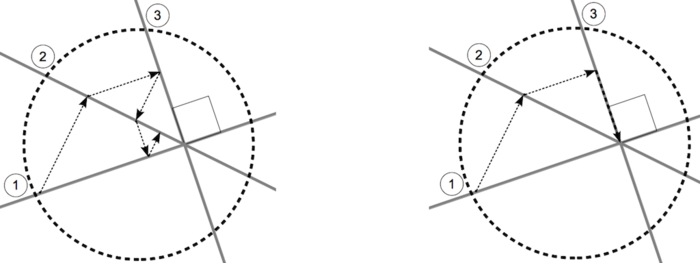
Как показано на Рис. 2 - итерационная последовательность, в случае Рис. 2 (справа) сходится вообще за конечное число итераций.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма Качмажа состоит из двух частей:
- предварительный расчет норм всех строк матрицы и задание начального приближения к решению,
- серия итераций на каждой из которых приближенное решение пересчитывается с использованием одной операций SAXPY (scalar multiplication and vector addition) [18].
Часть предварительного расчета необходима для оптимизации вычислений внутри итерационного процесса, для этого требуется выделение дополнительной памяти ([math]m[/math] числовых ячеек памяти) для хранения норм строк матрицы.
Расчет очередного приближения решения с.л.а.у. и оценки точности его вычисления выполняются в цикле вплоть до выхода по одному из условий:
- достижение необходимой точности;
- достижение максимального числа итераций.
Для расчета очередного приближения к решению используются такие макрооперации, как скалярное произведение, умножением вектора на число и сложение векторов.
Оценку сходимости последовательности можно проводить, например, по невязке (на что будут потрачены дополнительные вычислительные ресурсы) или контролируя норму разности приближенных решений между итерациями. Количество сложений, умножений и сравнений прямо пропорционально количеству итераций.
1.4 Макроструктура алгоритма
Опуская предварительный расчет, базовой макро-операцией алгоритма является операция SAXPY. Параллелизация алгоритма ограничена его итерационной природой, а эффективность параллельных реализаций операции SAXPY увеличивается с увеличением размерности (фактически с увеличением количества неизвестных в с.л.а.у. [math]n[/math]). Это особенно важно в задачах обработки изображений.
1.5 Схема реализации последовательного алгоритма
- Инициализируем вектор решения первым приближением: [math]u = u^{0}[/math]. В качестве первого приближения зачастую используется нулевой вектор.
- Рассчитываем нормы строк матрицы с.л.а.у.: [math]{\Vert A \Vert}[/math].
- Вычисляем очередной номер проекции: [math]j\left(k\right)=\left(k\ \bmod\ m\right)+1,\, k=\overline{0,\infty}[/math].
- Для целей обеспечения устойчивости, проверяем, что норма соответствующей проекции не близка к нулю и продолжаем вычисления, иначе переходим к новой итерации (пункт 3).
- Запоминаем предыдущее приближение решения и вычисляем новое: [math]u^{k+1}=u^{k}+\lambda_{k}\frac{f_{j\left(k\right)}-\left(a_{j\left(k\right)},u^{k}\right)}{\Vert a_{j\left(k\right)}\Vert^{2}}a_{j\left(k\right)}[/math].
- Если решение вычислено с заданной точностью, то выходим из цикла иначе переходим к новой итерации (пункт 3).
1.6 Последовательная сложность алгоритма
Вычислительная сложность алгоритма Качмажа определяется сложностью реализации операции SAXPY - [math]O(n)[/math]. Затраты на предварительный расчет обычно не включают в сложность самого алгоритма. В итоге, общая сложность алгоритма Качмажа зависит от количества итераций и равна [math]k \cdot O(n)[/math]. При этом в определенных случаях, можно сделать верхние оценки необходимого количества итераций для достижения заданной точности.
1.7 Информационный граф
Исходя из описания алгоритма можно построить информационный и операционные графы алгоритма (см. Рис. 2 и 3). В качестве вершин графа выступают этапы последовательного алгоритма (см. пункт 1.5). Графы алгоритма являются параметризованными (зависят от входных данных) и недетерминированными (в смысле, что количество вычислений зависит от начальных данных).
Из приведенных графов следует, что зависимость каждой итерации цикла от предыдущей исключает параллельную реализацию алгоритма. Фактически, в качестве подготовительных действий возможно одновременно рассчитать начальное приближение, нормы строк матрицы и порядок обхода (номера проекций), остальная часть алгоритма выполняется исключительно последовательно.
1.8 Ресурс параллелизма алгоритма
Алгоритм Качмажа, как любой итерационный алгоритм, является последовательным, в строковой версии алгоритма ресурс для параллелизма оказывается небольшим - только за счет параллельной реализации операции SAXPY.
Однако, существуют различные блочные версии алгоритма Качмажа, где проектирование осуществляется не на конкретную гиперплоскость, а на их пересечение в рамках выбранного блока. Такие модификации имеют существенно больший ресурс для распараллеливания и связаны с трудоемкими задачами вычисления псевдообратной матрицы и задаче выбора оптимального размера блока (в общем случае не предполагается, что матрица разбивается на блоки равных размеров, что еще больше усложняет задачу).
1.9 Входные и выходные данные алгоритма
Входными данными алгоритма являются матрица с.л.а.у. [math]A[/math], вектор правых частей [math]f[/math], требуемая точность [math]\epsilon[/math], а так же максимальное количество итераций [math]K_{max}[/math]. Выходными данными алгоритма является вектор решения с.л.а.у. [math]u[/math].
1.10 Свойства алгоритма
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Ниже представлен прототип программной реализации алгоритма на языке MatLab. Большое количество вариантов реализации и различных модификаций представлено в этих пакетах [19][20].
function [ u ] = ART(A, f, maxit, tol)
%ART1 - алгоритм алгебраической реконструкции (С. Качмажа) с циклическим обходом
% A, f - исходные данные задачи
% tol - чувствительность правила останова
[m,n] = size(A); u = zeros(n,1);
% Нормы строк матрицы с.л.а.у. рассчитываются заранее
nrma2 = full(abs(sum(A.*A',1)));
for k = 1:1:maxit
j = mod(k-1,m) + 1;
if (nrma2(j) <= 0), continue, end;
u_prev = u;
u = u + (f(j) - (A(j,:)*u))/nrma2(j) * A(j,:)';
if (norm(u_prev-u) <= tol), break, end;
end;
end;
В качестве критерия завершения итераций используют наиболее популярные правила останова (но не всегда эффективные): критерий останова по невязке [math]\left\Vert A\cdot u_{k}-f\right\Vert \lt \epsilon[/math] или [math]\left\Vert u_{k-1}-u_{k}\right\Vert \lt \epsilon[/math] (как в представленной реализации). Последний критерий может слишком рано завершать итерации, в виду того, что часто, алгоритм имеет медленную скорость сходимости.
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 ЧАСТЬ. Дополнительная информация
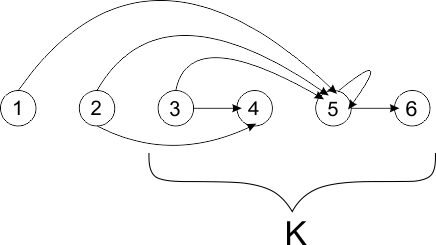
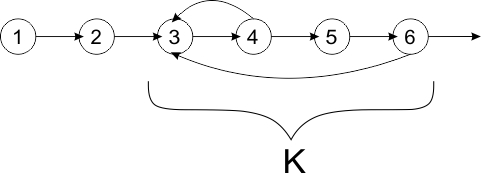
3.1 Классификация проекционных последовательностей
Под проекционной последовательностью понимается порядок обхода уравнений системы в процессе итераций алгоритма Качмажа. А рассматриваемая последовательность задается с использованием правила [math]j\left(k\right)[/math], где [math]k\in N_{0}[/math] которое позволяет вычислить номер используемого уравнения на итерации с номером [math]k[/math]. Правило [math]j\left(k\right)[/math]рассматривать как сюръективное отображение множества [math]N_{0}[/math] на множество [math]\left\{ 1,2,\ldots,m\right\}[/math], где [math]m[/math] - количество уравнений в с.л.а.у. [math]Au=f,\ A\in R^{m\times n},\ u\in R^{n},\ f\in R^{m}[/math].
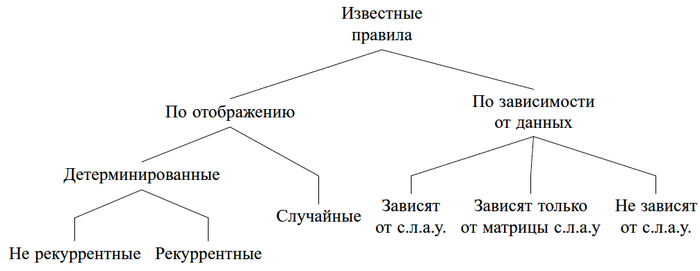
Отображения такого вида могут быть как детерминированными, так и случайными, рандомизированными. В последнем случае [math]j\left(k\right)[/math] является дискретной случайной величиной с заданным законом распределения. Например, к детерминированным отображениям необходимо отнести:
- правило циклического обхода [math]j\left(k\right)=\left(k\bmod m\right)+1,\, k=\overline{0,\infty}[/math];
- метод четной перестановки - эвристический метод для задач компьютерной томограции из [21];
- симметричное правило (symmetric ART), в котором последовательность проектирования на гиперплоскости идет в начале в прямом порядке от первого уравнения к последнему, а затем в обратном порядке - от последнего - к первому.
Существенно важной является классификация рассматриваемых правил по их зависимости от данных. Например, результат из [22], где [math]j\left(k\right)[/math] является дискретной случайной величиной с заданным законом распределения [math]P\left(j\left(k\right)=i\right)=\frac{\left\Vert a_{i}\right\Vert _{2}^{2}}{\left\Vert A\right\Vert _{F}^{2}}[/math], где [math]\left\Vert \cdot\right\Vert _{F}[/math] - матричная норма Фробениуса и [math]\left\Vert a_{i}\right\Vert[/math] - евклидова норма строки матрицы с.л.а.у. с номером [math]i=\overline{1,m}[/math]. Этот результат качественно отличается от всех известных рандомизированных способов наличием зависимости от матрицы с.л.а.у - от исходных данных задачи.
3.2 Рандомизированная версия алгоритма и скорость сходимости
3.3 Алгоритм Качмажа как метод максимального уменьшения ошибки на каждой итерации
3.4 Алгоритм Качмажа с четной перестановкой
3.5 Параллельные реализации
4 Литература
- ↑ Natterer, Frank (2001), "V.3 Kaczmarz's method", The Mathematics of Computerized Tomography, Classics in Applied Mathematics 32, SIAM, p. 128, ISBN 9780898714937.
- ↑ Kaczmarz, S. Angenäherte Auflösung von Systemen linearer Gleichungen [Текст] / S. Kaczmarz // Bulletin International de l'Académie Polonaise des Sciences et des Lettres / Classe des Sciences Mathématiques et Naturelles. Série A, Sciences Mathématiques. — 1937. — Vol. 35. — С. 355-357.
- ↑ Hounsfield, G. N. A Discussion on Recent Developments in Medical Endoscopy and Related Fields [Текст] / G. N. Hounsfield // Proceedings of the Royal Society of London. Series B, Biological Sciences. — 1977. — Vol. 195, N. 1119. — С. 281-289.
- ↑ Gordon, R. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography [Текст] / R. Gordon, R. Bender, G. T. Herman // Journal of theoretical biology. — 1970. — Vol. 29, Issue 3. — С. 471–481.
- ↑ Micke, A. The Mathematics of Computerized Tomography [Текст] / A. Micke, F. Natterer // ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik (Journal of Applied Mathematics and Mechanics). — 1987. — Vol. 67, Issue 11. — С. 580. —ISBN 3-519-02103-X and 0-471-90959-9.
- ↑ Herman, G. T. Fundamentals of computerized tomography: Image reconstruction from projection [Текст] : 2nd ed. / G. T. Herman. — Springer, 2009. — 300 с.
- ↑ Sezan, K. M. Applications of convex projection theory to image recovery in tomography and related areas [Текст] / K. M. Sezan, H. Stark // Image Recovery: Theory and Application / H. Stark, editor. — Academic Press, 1987. — С. 415-462.
- ↑ Cegielski, A. Bibliography on the Kaczmarz method [Электронный ресурс] : Faculty of Mathematics, Computer Science and Econometrics University of Zielona Gora ; Poland, March, 28th, 2010 / Режим доступа: http://www.uz.zgora.pl/~acegiels/Publikacje-Kaczmarz.pdf
- ↑ Ильин, В. П. Об итерационном методе Качмажа и его обобщениях [Текст] / В. П. Ильин // Сибирский журнал индустриальной математики. — 2006. — Т. 9, вып. 3. — С. 39–49.
- ↑ Г. П. Васильченко, А. А. Светлаков, “Проекционный алгоритм решения систем линейных алгебраических уравнений большой размерности”, Ж. вычисл. матем. и матем. физ., 20:1 (1980), 3–10.
- ↑ Л. Г. Гурин, Б. Т. Поляк, Э. В. Райк, “Методы проекций для отыскания общей точки выпуклых множеств”, Ж. вычисл. матем. и матем. физ., 7:6 (1967), 1211–1228
- ↑ Strohmer, T. A Randomized Kaczmarz Algorithm with Exponential Convergence [Текст] / T. Strohmer, R. Vershynin // Journal of Fourier Analysis and Applications. — 2009. — Vol. 15, Issue 2. — С. 262-278.
- ↑ Marks, L. D. A feasible set approach to the crystallographic phase problem [Текст] / L. D. Marks, W. Sinkler, E. Landree // Acta Crystallographica Section A. — 1987. — Vol. 55, Issue 4. — С. 601-612.
- ↑ JElble, J. M. GPU computing with Kaczmarz’s and other iterative algorithms for linear systems [Текст] / J. M. Elble, N. V. Sahinidis, P. Vouzis // Parallel Computing. — 2010. — Vol. 36, Issues 5-6. — С. 215–231.
- ↑ Bjorck, A. Accelerated projection methods for computing pseudoinverse solutions of systems of linear equations [Текст] / A. Bjorck, T. Elfving // BIT Numerical Mathematics. — 1979. — Vol. 19, Issue 2. — С.145-163.
- ↑ Nikazad, T. Algebraic Reconstruction Methods [Текст] : PhD. Thesis, Linköping University / T. Nikazad. — Linköping, 2008.
- ↑ Kamath, G. Component-Average Based Distributed Seismic Tomography in Sensor Networks [Текст] / G. Kamath, L. Shi, W.-Z. Song // IEEE International Conference on Distributed Computing in Sensor Systems. — 2013. — С. 88-95.
- ↑ Mark Harris. Six Ways to SAXPY https://devblogs.nvidia.com/parallelforall/six-ways-saxpy/
- ↑ Hansen, P. C. AIR Tools – A MATLAB package of algebraic iterative reconstruction methods [Электронный ресурс] / Режим доступа: http://www2.compute.dtu.dk/~pcha/AIRtools/
- ↑ Ivanov, A. A. Regularization Kaczmarz Tools Version 1.4 for Matlab, Matlabcentral Fileexchange [Электронный ресурс] / Режим доступа: http://www.mathworks.com/matlabcentral/fileexchange/43791
- ↑ Guan H. A projection access order for speedy convergence of ART (algebraic reconstruction technique): a multilevel scheme for computed tomography [Текст] / Guan H., R. Gordon // Physics in Medicine and Biology. — 1994. — Vol. 39, N. 11. — С. 2005-2022.
- ↑ Strohmer, T. A Randomized Kaczmarz Algorithm with Exponential Convergence [Текст] / T. Strohmer, R. Vershynin // Journal of Fourier Analysis and Applications. — 2009. — Vol. 15, Issue 2. — С. 262-278.