Участник:Anton goy/Самоорганизующиеся карты Кохонена: различия между версиями
Anton goy (обсуждение | вклад) |
Anton goy (обсуждение | вклад) |
||
| Строка 18: | Строка 18: | ||
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| − | Пусть <math>\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}</math> - некоторое подмножество точек пространства <math>\mathbb{R}^D</math>, <math>\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D</math>. В машинном обучении множество <math>\mathcal{L}</math> называют обучающей выборкой. Кроме того, задана структура слоя Кохонена: выбрана прямоугольная или шестиугольная связность между нейронами, задано общее количество нейронов (обозанчим его через <math>L = X \times Y</math>, где <math>X</math> и <math>Y</math> - количество нейронов в строках и столбцах соответственно), а также для каждого нейрона определено его положение в слое Кохонена <math>(x, y)</math>, где <math>x \in \left\{ 1, \dots, X \right\}</math>, а <math>y \in \left\{ 1, \dots, Y \right\}</math>. Пусть <math>\mathbf{w}_{x,y} = \left( w_{x,y}^{(1)}, \dots, w_{x,y}^{(D)} \right) \in \mathbb{R}^D</math> - вектор весов соответствующий нейрону в позиции <math>(x, y)</math>. | + | Пусть <math>\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}</math> - некоторое подмножество точек пространства <math>\mathbb{R}^D</math>, <math>\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D</math>. В машинном обучении множество <math>\mathcal{L}</math> называют обучающей выборкой. Кроме того, задана структура слоя Кохонена: выбрана прямоугольная или шестиугольная связность между нейронами, задано общее количество нейронов (обозанчим его через <math>L = X \times Y</math>, где <math>X</math> и <math>Y</math> - количество нейронов в строках и столбцах соответственно), а также для каждого нейрона определено его положение в слое Кохонена <math>\mathbf(x, y)</math>, где <math>x \in \left\{ 1, \dots, X \right\}</math>, а <math>y \in \left\{ 1, \dots, Y \right\}</math>. Пусть <math>\mathbf{w}_{x,y} = \left( w_{x,y}^{(1)}, \dots, w_{x,y}^{(D)} \right) \in \mathbb{R}^D</math> - вектор весов соответствующий нейрону в позиции <math>(x, y)</math>. |
'''Алгоритм обучения:''' | '''Алгоритм обучения:''' | ||
| − | 1. | + | 1. Найти начальное приближение весов <math>\mathbf{w}_{x,y}</math>, для <math>\forall x=1, \dots, X</math> и <math>\forall y=1, \dots, Y</math>. |
| + | |||
| + | 2. Выбрать случайно номер объекта <math>i \sim Unif[1, N]</math>. | ||
| + | |||
| + | 3. Для всех пар <math>(x, y)</math> найти расстояние между <math>\mathbf{x}_i</math> и вектором весов <math>\mathbf{w}_{x, y}</math> | ||
| + | |||
| + | :<math>\rho(\mathbf{x}_i, \mathbf{w}_{x, y}) = \left\| \mathbf{x}_i - \mathbf{w}_{x, y} \right\|^2, \quad \forall x=1, \dots, X, \forall y=1, \dots, Y</math> | ||
| + | |||
| + | 4. Найти нейрон-победитель <math>(x, y) = \arg \min_{\forall(x, y)} \rho(\mathbf{x}_i, \mathbf{w}_{x, y})</math>, наиболее близкий к текущему объекту <math>\mathbf{x}_i</math>. | ||
| + | |||
| + | 5. | ||
Версия 21:56, 22 сентября 2016
Автор: Гой Антон, 617 группа.
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Самоорганизующаяся карта Кохонена (англ. Self-Organizing Map или сокращено SOM) - это разновидность нейронных сетей, относящаяся к алгоритмам обучения без учителя. Основная цель - найти скрытые закономерности в данных по средством снижения размерности исходного пространства. Важным свойством карт Кохонена является то, что они строят отображение в пространство низкой размерности (обычно двумерное) таким образом, что топология исходного пространства сохраняется. Результат данного отображения - правильная решетка из обученных нейронов - называется "картой" исходного пространства. Алгоритм был разработан известным финским учёным, заслуженным академиком Финской Академии Наук Теуво Кохоненом в 1984(2) году. Карты Кохенана находят успешное применение в задачах кластеризации и визуализации, а также для снижения размерности и детектирования аномалий в данных.
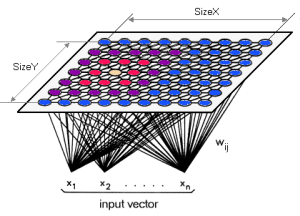
Карты Кохонена и по своей архитектуре, и по методу обучения отличаются от обычных нейронных сетей прямого распространения. C точки зрения метода обучения карты Кохонена не используют градиентные методы для минимизации ошибки (как это делается в сетях прямого распространения), поскольку являются алгоритмом обучения без учителя и никак не могут учитывать информацию и метках классов. Поэтому нейронная сеть обучается через соревнование между нейронами: на каждом шаге алгоритма для случайного объекта из обучающей выборки выбирается нейрон-победитель (best matching unit, BMU), который в определенном смысле похож на данный объект. А архитектура карты Кохонена представляет два слоя из нейронов: первый слой состоит из входных нейронов (их количество равно размерности исходного пространства), второй слой (его еще называют слоем Кохонена) представляет собой прямоугольную матрицу из нейронов, соедененных со всеми входами сети. Размеры матрицы выбираются вручную до начала запуска алгоритма.
Таким образом каждый нейрон слоя Кохонена описывается: вектором весов [math]\mathbf{w}[/math], размерность которого совпадает с размерностью исходного пространства, и его положением в слое Кохонена (индексы). Процесс обучения состоит в настройке векторов [math]\mathbf{w}[/math].
1.2 Математическое описание алгоритма
Пусть [math]\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}[/math] - некоторое подмножество точек пространства [math]\mathbb{R}^D[/math], [math]\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D[/math]. В машинном обучении множество [math]\mathcal{L}[/math] называют обучающей выборкой. Кроме того, задана структура слоя Кохонена: выбрана прямоугольная или шестиугольная связность между нейронами, задано общее количество нейронов (обозанчим его через [math]L = X \times Y[/math], где [math]X[/math] и [math]Y[/math] - количество нейронов в строках и столбцах соответственно), а также для каждого нейрона определено его положение в слое Кохонена [math]\mathbf(x, y)[/math], где [math]x \in \left\{ 1, \dots, X \right\}[/math], а [math]y \in \left\{ 1, \dots, Y \right\}[/math]. Пусть [math]\mathbf{w}_{x,y} = \left( w_{x,y}^{(1)}, \dots, w_{x,y}^{(D)} \right) \in \mathbb{R}^D[/math] - вектор весов соответствующий нейрону в позиции [math](x, y)[/math].
Алгоритм обучения:
1. Найти начальное приближение весов [math]\mathbf{w}_{x,y}[/math], для [math]\forall x=1, \dots, X[/math] и [math]\forall y=1, \dots, Y[/math].
2. Выбрать случайно номер объекта [math]i \sim Unif[1, N][/math].
3. Для всех пар [math](x, y)[/math] найти расстояние между [math]\mathbf{x}_i[/math] и вектором весов [math]\mathbf{w}_{x, y}[/math]
- [math]\rho(\mathbf{x}_i, \mathbf{w}_{x, y}) = \left\| \mathbf{x}_i - \mathbf{w}_{x, y} \right\|^2, \quad \forall x=1, \dots, X, \forall y=1, \dots, Y[/math]
4. Найти нейрон-победитель [math](x, y) = \arg \min_{\forall(x, y)} \rho(\mathbf{x}_i, \mathbf{w}_{x, y})[/math], наиболее близкий к текущему объекту [math]\mathbf{x}_i[/math].
5.