Участник:Anton goy/Самоорганизующиеся карты Кохонена: различия между версиями
Anton goy (обсуждение | вклад) |
Anton goy (обсуждение | вклад) |
||
| Строка 25: | Строка 25: | ||
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| − | Пусть <math>\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}</math> - некоторое подмножество точек пространства <math>\mathbb{R}^D</math>, <math>\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D</math>. В машинном обучении множество <math>\mathcal{L}</math> называют обучающей выборкой. | + | Пусть <math>\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}</math> - некоторое подмножество точек пространства <math>\mathbb{R}^D</math>, <math>\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D</math>. В машинном обучении множество <math>\mathcal{L}</math> называют обучающей выборкой. |
| + | |||
| + | Для каждого Пусть <math>\mathbf{w}_{x,y} = \left( w_{x,y}^{(1)}, \dots, w_{x,y}^{(D)} \right) \in \mathbb{R}^D</math> - вектор весов соответствующий нейрону в позиции <math>(x, y)</math>. | ||
'''Алгоритм обучения:''' | '''Алгоритм обучения:''' | ||
Версия 15:33, 9 октября 2016
Автор: Гой Антон, 617 группа.
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Самоорганизующаяся карта Кохонена (англ. Self-Organizing Map или сокращено SOM) - это разновидность нейронных сетей, относящаяся к алгоритмам обучения без учителя. Основная цель - найти скрытые закономерности в данных по средством снижения размерности исходного пространства. Важным свойством карт Кохонена является то, что они строят отображение в пространство низкой размерности (обычно двумерное) таким образом, что топология исходного пространства сохраняется. Результат данного отображения - правильная решетка из обученных нейронов - называется "картой" исходного пространства. Алгоритм был разработан известным финским учёным, заслуженным академиком Финской Академии Наук Теуво Кохоненом в 1984(2) году. Карты Кохенана находят успешное применение в задачах кластеризации и визуализации, а также для снижения размерности и детектирования аномалий в данных.
Карты Кохонена и по своей архитектуре, и по методу обучения отличаются от обычных нейронных сетей прямого распространения. C точки зрения метода обучения, карты Кохонена не используют градиентные методы для минимизации ошибки (как это делается в сетях прямого распространения), поскольку являются алгоритмом обучения без учителя и никак не могут учитывать информацию и метках классов. Поэтому нейронная сеть обучается через соревнование между нейронами: на каждом шаге алгоритма для случайного объекта из обучающей выборки выбирается нейрон-победитель (best matching unit, BMU), который в определенном смысле наиболее похож на данный объект.
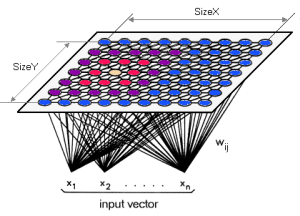
А архитектура карты Кохонена (Рис. 1) представляет два слоя: первый слой состоит из входных нейронов (их количество равно размерности исходного пространства), второй слой (его называют слоем Кохонена) представляет собой строго упорядоченную решетку, в узлах которой расположены нейроны-сумматоры, соедененные со всеми входами сети. Для задания топологии слоя Кохонена (Рис. 2) используют либо шестиугольные (Рис. 2а), либо прямоугольные (Рис. 2б) ячейки, в которых распологаются нейроны. Шестиугольные ячейки часто являются более предпочтительными, так как расстояние от центра выбранной ячейки до ее соседей одинаково.
Каждый нейрон [math]n_j[/math] слоя Кохонена описывается вектором весов [math]\mathbf{w}_j[/math], размерность которого совпадает с размерностью исходного пространства, и координатами нейрона на двумерной плоскости - [math]\mathbf{r}_j[/math].
Процесс обучения состоит в настройке векторов весов [math]\mathbf{w}_j[/math].
1.2 Математическое описание алгоритма
Пусть [math]\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}[/math] - некоторое подмножество точек пространства [math]\mathbb{R}^D[/math], [math]\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D[/math]. В машинном обучении множество [math]\mathcal{L}[/math] называют обучающей выборкой.
Для каждого Пусть [math]\mathbf{w}_{x,y} = \left( w_{x,y}^{(1)}, \dots, w_{x,y}^{(D)} \right) \in \mathbb{R}^D[/math] - вектор весов соответствующий нейрону в позиции [math](x, y)[/math].
Алгоритм обучения:
1. Найти начальное приближение весов [math]\mathbf{w}_{x,y}[/math], для [math]\forall x=1, \dots, X[/math] и [math]\forall y=1, \dots, Y[/math].
2. Выбрать случайно номер объекта [math]i \sim Unif[1, N][/math].
3. Для всех пар [math](x, y)[/math] найти расстояние между [math]\mathbf{x}_i[/math] и вектором весов [math]\mathbf{w}_{x, y}[/math]
- [math]\rho(\mathbf{x}_i, \mathbf{w}_{x, y}) = \left\| \mathbf{x}_i - \mathbf{w}_{x, y} \right\|^2, \quad \forall x=1, \dots, X, \forall y=1, \dots, Y[/math]
4. Найти нейрон-победитель [math](x^*, y^*) = \arg \min_{\forall(x, y)} \rho(\mathbf{x}_i, \mathbf{w}_{x, y})[/math], наиболее близкий к текущему объекту [math]\mathbf{x}_i[/math].
5. Для всех неронов [math](x, y)[/math] пересчитать их веса по следующей формуле:
- [math]\mathbf{w}_{x, y} \leftarrow \mathbf{w}_{x, y} + \alpha(t)h_{x^*, y^*}(t)(\mathbf{x}_i - \mathbf{w}_{x, y})[/math],
где [math]\alpha(t)[/math] - темп обучения (learning rate), монотонно убывающая функция от номера итерации [math]t[/math]; [math]h_{x^*, y^*}(t) = [/math]