Участник:Tikhomirov.mm/Алгоритм устойчивой кластеризации с иcпользованием связей (robust clustering using links, ROCK): различия между версиями
ASA (обсуждение | вклад) |
|||
| (не показано 37 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Основные авторы описания: [[Участник:Простов В. А.|В.А.Простов]](1.1 - 1.6, | + | {{Assignment|Teplov}} |
| − | + | {{algorithm | |
| − | + | | name = Алгоритм устойчивой кластеризации с использованием связей | |
| + | | serial_complexity = <math> O(n^2 + n m_m m_a + n^2 \log{} n)</math> | ||
| + | | input_data = Множество <math>S</math> из <math>n</math> элементов, число кластеров <math>k</math> | ||
| + | | output_data = <math>n</math> точек с метками <math>k</math> кластеров | ||
| + | }} | ||
| + | Основные авторы описания: [[Участник:Простов В. А.|В.А.Простов]](1.1 - 1.6, 1.9, 2.4), [[Участник:Tikhomirov.mm|М.М.Тихомиров]](1.7, 1.8, 1.10, 2.4, 2.7) | ||
= ЧАСТЬ. Свойства и структура алгоритмов = | = ЧАСТЬ. Свойства и структура алгоритмов = | ||
| Строка 27: | Строка 32: | ||
Функция, определяющая соседство двух точек: | Функция, определяющая соседство двух точек: | ||
| − | <math> | + | :<math> |
\begin{align} | \begin{align} | ||
neib(p_i, p_j) = \begin{cases} | neib(p_i, p_j) = \begin{cases} | ||
| Строка 39: | Строка 44: | ||
Функция, определяющая количество связей между точками: | Функция, определяющая количество связей между точками: | ||
| − | <math> | + | :<math> |
link(p_i, p_j) = \sum_{s\in S} neib(p_i,s) neib(p_j,s). | link(p_i, p_j) = \sum_{s\in S} neib(p_i,s) neib(p_j,s). | ||
</math> | </math> | ||
| Строка 45: | Строка 50: | ||
Определим теперь целевую функцию, считая <math>n_i</math> количеством элементов в <math>C_i</math>: | Определим теперь целевую функцию, считая <math>n_i</math> количеством элементов в <math>C_i</math>: | ||
| − | <math> | + | :<math> |
E_l = \sum_{i=1}^{k} n_i * \sum_{p_q, p_r \in C_i} \frac{link(p_q,p_r)}{n_{i}^{1+2f( \theta )}} | E_l = \sum_{i=1}^{k} n_i * \sum_{p_q, p_r \in C_i} \frac{link(p_q,p_r)}{n_{i}^{1+2f( \theta )}} | ||
</math> | </math> | ||
| Строка 51: | Строка 56: | ||
Определим функцию связи для двух подмножеств <math> C_i, C_j </math>: | Определим функцию связи для двух подмножеств <math> C_i, C_j </math>: | ||
| − | <math> | + | :<math> |
link[C_i, C_j] = \sum_{p_q \in C_i, p_r \in C_j} link(p_i, p_j) | link[C_i, C_j] = \sum_{p_q \in C_i, p_r \in C_j} link(p_i, p_j) | ||
</math> | </math> | ||
| Строка 57: | Строка 62: | ||
Введем функцию полезности, выражающую то, насколько выгодно объединить подмножества <math> C_i, C_j </math>: | Введем функцию полезности, выражающую то, насколько выгодно объединить подмножества <math> C_i, C_j </math>: | ||
| − | <math> | + | :<math> |
g(C_i, C_j) = \frac{link[C_i,C_j]}{(n_i + n_j)^{1+2f( \theta )} - n_i^{1+2f( \theta )} - n_j^{1+2f( \theta )}} | g(C_i, C_j) = \frac{link[C_i,C_j]}{(n_i + n_j)^{1+2f( \theta )} - n_i^{1+2f( \theta )} - n_j^{1+2f( \theta )}} | ||
</math> | </math> | ||
| Строка 123: | Строка 128: | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| − | Вычисление связей может рассматриваться как перемножение двух матриц размера <math | + | Вычисление связей может рассматриваться как перемножение двух матриц размера <math> n </math>, что можно реализовать за <math> O(n^{2.37})</math>. Затраты памяти на хранение связей не превышают <math> n(n+1)/2 </math>, когда любая пара точек - соседние. Однако в большинстве случаев среднее число соседей <math> m_a </math> и максимальное число соседей <math> m_m </math> значительно меньше <math> n </math>, в связи с этим оценки сложности зависят от данных параметров. Сложность построения списка соседей оценивается <math> O(n^2)</math>. Для каждой точки, после вычисления списка своих соседей, алгоритм рассматривает все пары его соседей. Для каждой пары точка вносит одну связь. Если процесс повторяется для каждой точки |
| + | и счетчик ссылок увеличивается на единицу для каждой пары соседей, то в конце концов, ссылка рассчитывает на | ||
| + | будут получены все пары точек. Если <math>m_i</math> - число соседей точки <math>i</math>, тогда для нее мы должны увеличить количество связей на единицу <math>m_i^2</math> раз. Таким образом, сложность алгоритма является <math>\sum m_i^2</math> и может быть оценено <math> O(n m_m m_a)</math>. Поскольку каждая точка <math>i</math> может иметь не более <math>\min \{ m_m m_i, n \} )</math> связей, то общие затраты памяти не превышают <math> O(\min \{ n m_m m_a, n^2 \} )</math>. | ||
Построение каждой кучи потребует не более <math> O(n)</math> времени (поскольку размер каждой кучи не может превышать <math> n </math>) Сортировка каждой кучи потребует <math> O( n \log{} n)</math>. Рассмотрим теперь основной while-цикл. Он содержит <math> O(n)</math> итераций, где основная сложность каждого шага приходится на for-цикл. В худшем случае потребуется вставить новый кластер в <math> O(n)</math> локальных куч размера <math> n</math>, что потребует <math> O( n \log{} n)</math> времени. Таким образом, сложность всего внешнего цикла составляет <math> O(n^2 \log{} n)</math> в худшем случае. Затраты памяти зависят от начального размера локальных куч, поскольку при слиянии кластеров их старые кучи удаляются, а размер новой не превышает суммы старых. Поскольку каждая куча сожержит лишь кластеры с ненулевыми связями, то сложность совпадает с первой частью и равна <math> O(\min \{ n m_m m_a, n^2 \} )</math>. | Построение каждой кучи потребует не более <math> O(n)</math> времени (поскольку размер каждой кучи не может превышать <math> n </math>) Сортировка каждой кучи потребует <math> O( n \log{} n)</math>. Рассмотрим теперь основной while-цикл. Он содержит <math> O(n)</math> итераций, где основная сложность каждого шага приходится на for-цикл. В худшем случае потребуется вставить новый кластер в <math> O(n)</math> локальных куч размера <math> n</math>, что потребует <math> O( n \log{} n)</math> времени. Таким образом, сложность всего внешнего цикла составляет <math> O(n^2 \log{} n)</math> в худшем случае. Затраты памяти зависят от начального размера локальных куч, поскольку при слиянии кластеров их старые кучи удаляются, а размер новой не превышает суммы старых. Поскольку каждая куча сожержит лишь кластеры с ненулевыми связями, то сложность совпадает с первой частью и равна <math> O(\min \{ n m_m m_a, n^2 \} )</math>. | ||
| Строка 131: | Строка 138: | ||
'''Сложность по времени''': | '''Сложность по времени''': | ||
| − | <math> O(n^2 + n m_m m_a + n^2 \log{} n)</math> | + | :<math> O(n^2 + n m_m m_a + n^2 \log{} n)</math> |
'''Сложность по памяти''': | '''Сложность по памяти''': | ||
| − | <math> O(\min \{ n^2, n m_m m_a \} )</math> | + | :<math> O(\min \{ n^2, n m_m m_a \} )</math> |
| + | |||
| + | '''Список обозначений''': | ||
| + | |||
| + | :<math> m_a </math> - среднее число соседей | ||
| + | |||
| + | :<math> m_m </math> - максимальное число соседей | ||
| + | |||
| + | :<math>m_i</math> - число соседей точки <math>i</math> | ||
| + | |||
| + | :<math>n</math> - размер входных данных | ||
== Информационный граф == | == Информационный граф == | ||
| − | [[Файл:Graph_tikh.png]] | + | [[Файл:Graph_tikh.png|400px|thumb|рис 1. Граф в общем виде для n точек и k кластеров.]] |
| + | Обозначения : | ||
| + | * '''CN''' - вершина построения соседей: заполнение nbrlist[i]. | ||
| + | * '''CLM''' - вершина построения матрицы связей: заполнение link[i][j]. | ||
| + | * '''CLH''' - вершина построения локальных куч: заполнение q[i]. | ||
| + | * '''CGH''' - вершина построения глобальной кучи: заполнение Q. | ||
| + | * '''GC''' - вершина поиска и слияние топ 2 кластеров: построение w. | ||
| + | * '''RL''' - пересчет матрицы связей: заполнение link[x,w]. | ||
| + | * '''UPDATE''' - Обновление глобальной кучи: обновление Q. | ||
| + | |||
Как видно из графа в алгоритме есть ряд узких мест. | Как видно из графа в алгоритме есть ряд узких мест. | ||
| − | |||
Рассмотрим их подробнее: | Рассмотрим их подробнее: | ||
1) Вершина построения матрицы links. Данные вычисления не могут быть прямо распараллелены, нельзя для каждого списка соседей запустить данную функцию. Это связано с тем, что во время выполнения данных вычислений необходимо производить запись в матрицу и любой список может писать в любое место матрицы. В худшем случае (когда все соседи всем) при параллельном запуске возможны постоянные конфликты. Но в данной вершине все же есть потенциал для параллельной работы. Он заключается в том, что можно в параллели обрабатывать список соседей. При подходе в лоб нагрузка на ядра будет не равномерна. | 1) Вершина построения матрицы links. Данные вычисления не могут быть прямо распараллелены, нельзя для каждого списка соседей запустить данную функцию. Это связано с тем, что во время выполнения данных вычислений необходимо производить запись в матрицу и любой список может писать в любое место матрицы. В худшем случае (когда все соседи всем) при параллельном запуске возможны постоянные конфликты. Но в данной вершине все же есть потенциал для параллельной работы. Он заключается в том, что можно в параллели обрабатывать список соседей. При подходе в лоб нагрузка на ядра будет не равномерна. | ||
| − | Так же данный пункт можно реализовать иначе. Но затраты по памяти возрастут в N раз. Можно параллельно обрабатывать каждый вектор соседей. При среднем количестве соседей <math>m_a</math> это займет <math>O( | + | Так же данный пункт можно реализовать иначе. Но затраты по памяти возрастут в N раз. Можно параллельно обрабатывать каждый вектор соседей. При среднем количестве соседей <math>m_a</math> это займет <math>O(m_a ^ 2)</math> операций (или если мы имеем <math>n^2</math> ядер, то можно и за <math>O(m_a)</math> + <math>O(log(n))</math> для объединения N матриц. |
2) Вершина построения глобальной кучи. В данной вершине необходимо добавить все вершины и после отсортировать в зависимости от наилучшего значения полезности каждой локальной кучи. Сортировку можно распараллелить. | 2) Вершина построения глобальной кучи. В данной вершине необходимо добавить все вершины и после отсортировать в зависимости от наилучшего значения полезности каждой локальной кучи. Сортировку можно распараллелить. | ||
| − | 3) Вершина взятия топ 2 кластеров. Узкая но малозатратная вершина. | + | 3) Вершина взятия топ 2 кластеров. Узкая, но малозатратная вершина. |
4) Вершина обновления куч. Так же узкая вершина в которой нужно в каждой локальной куче вставить в нужное место кластер и так же поступить с глобальной кучей. | 4) Вершина обновления куч. Так же узкая вершина в которой нужно в каждой локальной куче вставить в нужное место кластер и так же поступить с глобальной кучей. | ||
| Строка 161: | Строка 186: | ||
1) На первом этапе происходит вычисление соседей. Затраты данных операций при условии достаточного количества ядер <math>T_1 = O(n)</math> | 1) На первом этапе происходит вычисление соседей. Затраты данных операций при условии достаточного количества ядер <math>T_1 = O(n)</math> | ||
| − | 2) На этапе построения связей <math>n</math> этапов в каждом из которых можно сделать <math> | + | 2) На этапе построения связей <math>n</math> этапов в каждом из которых можно сделать <math>m</math> расчетов(с учетом распараллеливания), где <math>m</math> - количество соседей. В худшем случае <math>T_2 = O(n^2)</math> в среднем случае <math>T_2 = O(n * m_a)</math>, где <math>m_a</math> среднее ожидаемое число соседей. |
3) Построение одной кучи это сложность <math>O(n)</math>. Плюс для каждой кучи сортировка <math>O(n * log(n))</math>. Соответственно итоговая сложность создания локальных куч <math>T_3 = O(n * log(n))</math>. | 3) Построение одной кучи это сложность <math>O(n)</math>. Плюс для каждой кучи сортировка <math>O(n * log(n))</math>. Соответственно итоговая сложность создания локальных куч <math>T_3 = O(n * log(n))</math>. | ||
| Строка 168: | Строка 193: | ||
5) Цикл в котором происходит выбор кластеров, сливание, пересчет и обновление куч. Игнорируем выбор кластеров (достать из кучи <math>O(1)</math> ). Для всех элементов кучи слитых кластеров пересчитываем значение связи, вставляем в кучу выбранного кластера информацию о новом кластере, удаляем старое. Делается это за <math>O(log(n))</math>. Соответственно в худшем случае, одна итерация цикла это <math>T_i = O(log(n))</math>. | 5) Цикл в котором происходит выбор кластеров, сливание, пересчет и обновление куч. Игнорируем выбор кластеров (достать из кучи <math>O(1)</math> ). Для всех элементов кучи слитых кластеров пересчитываем значение связи, вставляем в кучу выбранного кластера информацию о новом кластере, удаляем старое. Делается это за <math>O(log(n))</math>. Соответственно в худшем случае, одна итерация цикла это <math>T_i = O(log(n))</math>. | ||
| − | Количество итераций n - k. Значит <math>T_5 = O((n - k) * log(n))</math>. При k = 1, <math>T_5 = O(n * log(n)</math> | + | Количество итераций n - k. Значит |
| + | |||
| + | :<math>T_5 = O((n - k) * log(n))</math>. При k = 1, <math>T_5 = O(n * log(n))</math> | ||
Итоговая сложность в худшем случае равна: | Итоговая сложность в худшем случае равна: | ||
| − | <math>T_1 + T_2 + T_3 + T_4 + T_5 = O(n) + O(n^2) + O(n * log(n)) + O(n * log(n)) + O(n * log(n)) = O(n^2)</math> | + | :<math>T_1 + T_2 + T_3 + T_4 + T_5 = O(n) + O(n^2) + O(n * log(n)) + O(n * log(n)) + O(n * log(n)) = O(n^2)</math> |
Итоговая сложность в среднем случае равна: | Итоговая сложность в среднем случае равна: | ||
| − | <math>O(n * m_a) + O(n * log(n))</math>. Тут важно понимать, что в зависимости от данных как <math>log(n)</math> может быть больше <math>m_a</math>, так и наоборот. | + | :<math>O(n * m_a) + O(n * log(n))</math>. |
| + | |||
| + | Тут важно понимать, что в зависимости от данных как <math>log(n)</math> может быть больше <math>m_a</math>, так и наоборот. | ||
| + | |||
| + | <b>Сложность по времени:</b> | ||
| + | |||
| + | :<math>O(n * (m_a + log(n)))</math>. | ||
== Входные и выходные данные алгоритма == | == Входные и выходные данные алгоритма == | ||
| Строка 189: | Строка 222: | ||
== Свойства алгоритма == | == Свойства алгоритма == | ||
| − | + | Алгоритм является детерминированным. | |
| − | + | Алгоритм является устойчивым. | |
| − | + | Вычислительная мощность алгоритма равна: | |
| − | + | :<math>\frac{O(n^2 + n m_m m_a + n^2 \log{} n)}{n}</math>. | |
| − | + | Отношение последовательной и параллельной сложности: | |
| − | + | :<math>\frac{O(n^2 + n m_m m_a + n^2 \log{} n)}{O(n * (m_a + log(n)))}</math>. | |
| + | |||
| + | |||
| + | К свойствам алгоритма можно отнести то, что сложность в среднем зависит от данных. Если растет среднее ожидаемое количество соседей, то растет и средняя сложность алгоритма. В худшем случае она может достигать <math>O(n^2)</math> для данных с большой кучностью (одна большая плотная куча, где по факту 1 кластер). Но, если же среднее ожидаемое число соседей меньше <math>log(n)</math>, то сложность алгоритма будет <math>O(n *log(n))</math>. В целом можно взять оценку <math>O(n * m_m)</math>, где <math> m_m </math> максимальное количество соседей. | ||
= ЧАСТЬ. Программная реализация алгоритма = | = ЧАСТЬ. Программная реализация алгоритма = | ||
| Строка 213: | Строка 249: | ||
== Масштабируемость алгоритма и его реализации == | == Масштабируемость алгоритма и его реализации == | ||
| + | === Масштабируемость алгоритма === | ||
| + | Как можно видеть из графа, представленного выше, в алгоритме есть 3 основных места для распараллеливания: | ||
| + | 1) Составление матрицы связей | ||
| + | 2) Построение локальных куч | ||
| + | 3) Основной цикл алгоритма | ||
| + | |||
| + | Теоретическая оценка сложности алгоритма распараллеленного на p потоков: | ||
| + | :<math>O(\frac{n}{p}(n + m_m m_a + n\log{} n))</math>. | ||
| + | |||
| + | Соответственно: | ||
| + | 1) При одинаковых входных данных, время работы обратно пропорционально количеству потоков. | ||
| + | 2) При одинаковом количестве потоков, время зависит от входных данных кубически в худшем случае. | ||
| + | |||
| + | === Масштабируемость реализации === | ||
| + | Реализация алгоритма тестировалась на IBM pSeries 690 HPC Regatta. | ||
| + | * Максимальное количество потоков, способных работать в параллельном режиме: 16. | ||
| + | * Процессоры POWER4 1,3 ГГц; 16-процессорная архитектура SMP | ||
| + | |||
| + | Параметры запусков: | ||
| + | 1) Запуски осуществлялись на задачах объемом 400, 800, 1600, 2400 точек. | ||
| + | 2) Запуски осуществлялись на 1, 2, 4, 8, 16 потоках. | ||
| + | 3) Количество кластеров = 2, <math>\theta</math> = 0.3, соседями считались все точки в радиусе 0.3 . | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Количество потоков / Количество точек | ||
| + | ! 400 | ||
| + | ! 800 | ||
| + | ! 1200 | ||
| + | ! 1600 | ||
| + | |- | ||
| + | | 1 | ||
| + | | 23 с. | ||
| + | | 188 с. | ||
| + | | 631 с. | ||
| + | | 1514 с. | ||
| + | |- | ||
| + | | 2 | ||
| + | | 17 с | ||
| + | | 134 с | ||
| + | | 452 с | ||
| + | | 1079 с | ||
| + | |- | ||
| + | | 4 | ||
| + | | 10 с | ||
| + | | 79 с | ||
| + | | 268 с | ||
| + | | 631 с | ||
| + | |- | ||
| + | | 8 | ||
| + | | 8 с | ||
| + | | 45 с | ||
| + | | 144 с | ||
| + | | 342 с | ||
| + | |- | ||
| + | | 16 | ||
| + | | 4 с | ||
| + | | 24 с | ||
| + | | 79 с | ||
| + | | 185 с | ||
| + | |} | ||
| + | |||
| + | Как видно из таблицы, масштабируемость реализации коррелирует с теоретической оценкой. | ||
| + | |||
| + | Наглядно эти данные можно увидеть на следующем изображении. | ||
| + | [[Файл:Rock regatta.png|1200px|center|thumb|рис 2. Масштабируемость реализации]] | ||
| + | |||
| + | |||
| + | |||
| + | Реализация доступна по ссылке на github [https://github.com/refalc/rock_cmc_msu/] | ||
== Динамические характеристики и эффективность реализации алгоритма == | == Динамические характеристики и эффективность реализации алгоритма == | ||
Текущая версия на 16:05, 3 февраля 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 03.02.2017 Данная работа соответствует формальным критериям. Проверено Teplov. |
| Алгоритм устойчивой кластеризации с использованием связей | |
| Последовательный алгоритм | |
| Последовательная сложность | [math] O(n^2 + n m_m m_a + n^2 \log{} n)[/math] |
| Объём входных данных | Множество [math]S[/math] из [math]n[/math] элементов, число кластеров [math]k[/math] |
| Объём выходных данных | [math]n[/math] точек с метками [math]k[/math] кластеров |
Основные авторы описания: В.А.Простов(1.1 - 1.6, 1.9, 2.4), М.М.Тихомиров(1.7, 1.8, 1.10, 2.4, 2.7)
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Алгоритм устойчивой кластеризации с иcпользованием связей ROCK (RObust Clustering using linKs) был совместно разработан Sudipto Guha, Rajeev Rastogi и Kyuseok Shim при работе в Bell Laboratories. Впервые алгоритм был опубликован в 1999 году в статье под названием "ROCK: A Robust Clustering Algorithm for Categorical Attributes", входящей в "ICDE '99 Proceedings of the 15th International Conference on Data Engineering".
Данный алгоритм принадлежит классу алгоритмов кластеризации, целью которых является разбиение данных на некоторое заранее заданное число групп. Подобные методы часто используются для анализа данных в различных областях, в том числе в маркетинге. Основная особенность алгоритма ROCK заключается в использовании связей между точками (количество общих соседей), в отличие от методов, базирующихся на различных метриках, таких как расстояние между точками (Евклидово и прочие). Такой подход улучшает определение глобальных зависимостей, а также наиболее эффективен при рассмотрении данных, свойства которых принимают достаточно малое конечное количество значений.
Одним из основных понятий для алгоритма ROCK является соседство двух точек. Пусть нам дана функция схожести [math] sim(p_i,p_j) [/math], принимающая значения от 0 до 1, которая выражает схожесть или близость объектов(точек) [math]p_i[/math] и [math]p_j[/math]. Предполагается, что 1 соответствует абсолютной близости, и 0 - наоборот. Тогда при некоторой границе [math]\theta[/math] между 0 и 1, если [math] sim(p_i,p_j) \geq \theta [/math], то [math]p_i[/math] и [math]p_j[/math] будут соседними точками. Выбор Функции [math] sim(p_i,p_j) [/math] и граничного значения [math]\theta[/math] зависит входных данных и особенности реализации.
Вторым ключевым понятием являются связи. Функция связи [math] link(p_i,p_j) [/math] определяется как количество общих соседей у [math]p_i[/math] и [math]p_j[/math]. Из такого определения сразу видно, что чем больше значение связи, тем больше вероятность, что эти точки принадлежат одному и тому же кластеру. Такой подход является более глобальным, по сравнению с использованием только близости двух точек, что позволяет снизить число ошибок, особенно в тех случаях, когда кластеры имеют несколько близких точек.
Алгоритм состоит из двух основных этапов. Изначально имеется [math]n[/math] точек и [math]k[/math] - желаемое число кластеров. На первом этапе вычисляются значения связей [math] link(p_i,p_j) [/math] между всеми парами точек, каждая точка объявляется отдельным кластером. Для каждого кластера [math]i[/math] создается локальная куча [math]q[i][/math], которая содержит все такие кластеры [math]j[/math], что связь между ними не нулевая. Кроме этого, создается глобальная куча [math]Q[/math], содержащая все кластеры. После этого алгоритм переходит ко второму этапу. Вторая часть представляет из себя цикл, на каждом шаге которого объединяются два кластера с максимальным значением функции полезности [math]g(i,j)[/math], после чего вносятся соответствующие изменения в кучи. Алгоритм завершает работу в двух случаях: когда осталось [math]k[/math] кластеров, или когда все связи между оставшимися кластерами равны нулю.
1.2 Математическое описание алгоритма
Дано множество [math] S [/math] из [math] n [/math] элементов и число [math] k [/math]. Для каждых [math] p_i,p_j \in S [/math] задана функция схожести [math] 0 \leq sim(p_i,p_j) \leq 1[/math]. Также дано число [math] 0 \leq \theta \leq 1[/math]. Дана функция [math] f( \theta ) [/math].
Требуется разбить [math] S [/math] на [math] k [/math] не пересекающихся подмножеств(кластеров) [math]C_1, \dots, C_k[/math] так, чтобы значение целевой функции [math]E_l[/math]было как можно большим.
Определим следующие функции, полагая, что [math] p_i,p_j \in S. [/math]
Функция, определяющая соседство двух точек:
- [math] \begin{align} neib(p_i, p_j) = \begin{cases} 1, sim(p_i, p_j) \geq \theta,\\ 0, sim(p_i, p_j) \lt \theta. \end{cases} \\ \end{align} [/math]
Функция, определяющая количество связей между точками:
- [math] link(p_i, p_j) = \sum_{s\in S} neib(p_i,s) neib(p_j,s). [/math]
Определим теперь целевую функцию, считая [math]n_i[/math] количеством элементов в [math]C_i[/math]:
- [math] E_l = \sum_{i=1}^{k} n_i * \sum_{p_q, p_r \in C_i} \frac{link(p_q,p_r)}{n_{i}^{1+2f( \theta )}} [/math]
Определим функцию связи для двух подмножеств [math] C_i, C_j [/math]:
- [math] link[C_i, C_j] = \sum_{p_q \in C_i, p_r \in C_j} link(p_i, p_j) [/math]
Введем функцию полезности, выражающую то, насколько выгодно объединить подмножества [math] C_i, C_j [/math]:
- [math] g(C_i, C_j) = \frac{link[C_i,C_j]}{(n_i + n_j)^{1+2f( \theta )} - n_i^{1+2f( \theta )} - n_j^{1+2f( \theta )}} [/math]
В данном алгоритме сначала все элементы разбиваются на [math] n [/math] подмножеств, затем делается [math] n - k [/math] шагов, на каждом из которых объединяются два подмножества, для которых значение функции полезности [math] g(i,j) [/math] наибольшее.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из двух основных частей.
1. Вычисление всех связей между точками. Для каждой точки создается список соседей. Проходим по каждому такому списку и увеличиваем количество связей между всеми точками из списка, поскольку они имеют общую соседнюю точку (ту, которой принадлежит список).
2. Цикл по объединению кластеров, содержит [math] n-k [/math] шагов, на каждом из которых мы находим наилучшие кластеры для объединения и перестраиваем соответствующие кучи.
1.4 Макроструктура алгоритма
Как написано в описании ядра алгоритма, алгоритм состоит из двух основных частей: Вычисление связей и Объединение кластеров.
1.5 Схема реализации последовательного алгоритма
Процедура кластеризации выглядит следующим образом:
procedure cluster(S, k) begin link := compute_links(S) for each s [math]\in[/math] S do q[s] := build_local_heap(link, s) Q := build_global_heap(S, q) while size(Q) > k do { u := extract_max(Q) v := max(q[u]) delete(Q, v) w := merge(u, v) for each x [math]\in[/math] q[u] [math]\cup[/math] q[v] do { link[x,w] := link[x, u] + link[x, v] delete(q[x], u); delete(q[x], v) insert(q[x],w, g(x,w)); insert(q[w], x, g(x,w)) update(Q, x, q[x]) } insert(Q,w, q[w]) deallocate(q[u]), deallocate(q[v]) } end
1. Вычисление связей между каждой парой точек:
procedure compute_links(S)
begin
Compute nbrlist[i] for every point i in S
Set link[i, j] to be zero for all i, j
for i := 1 to n do {
N := nbrlist[i]
for j := 1 to |N| - 1 do
for l := j + 1 to |N| do
link[N[j],N[l]] := link[N[j],N[l]] + 1
}
end
Дла каждой точки [math]i[/math] строится список соседей [math]nbrlist[i][/math]. Поскольку любые две точки в таком списке имеют nbrlist[i] в качестве общего соседа, то для всех пар точек из списка увеличиваем значение функции связей.
2. Каждая точка объявляется отдельным кластером. Для каждого кластера [math]i[/math] строится локальная куча [math]q[i][/math], которая поддерживается до конца работы алгоритма. [math]q[i][/math] содержит все такие кластеры [math]j[/math], что [math]link[i,j] \neq 0[/math]. Кластеры [math]j[/math] в [math]q[i][/math] отсортированы в порядке убывания функции полезности [math]g(i,j)[/math]. Аналогичным образом создается глобальная куча [math]Q[/math], содержащая все кластеры. Элементы внутри аналогично отсортированы в соответствии с их максимальным значением функции полезности.
3. Запускается while-цикл до тех пор, пока количество кластеров не станет равно [math]k[/math]. На каждом шаге цикла берутся два кластера с максимальным значением [math]g(i,j)[/math] и объединяются. Из глобальной кучи извлекается максимум, затем для этого кластера из его локальной кучи также извлекается максимум. По построению куч легко видеть, что это будет искомой парой. Далее происходит объединение кластеров, после чего для каждого кластера, который содержал в своей локальной куче один из данных, необходимо провести соответствующую коррекцию. Из глобальной кучи также удаляются два элемента и добавляется один новый с сохранением порядка.
1.6 Последовательная сложность алгоритма
Вычисление связей может рассматриваться как перемножение двух матриц размера [math] n [/math], что можно реализовать за [math] O(n^{2.37})[/math]. Затраты памяти на хранение связей не превышают [math] n(n+1)/2 [/math], когда любая пара точек - соседние. Однако в большинстве случаев среднее число соседей [math] m_a [/math] и максимальное число соседей [math] m_m [/math] значительно меньше [math] n [/math], в связи с этим оценки сложности зависят от данных параметров. Сложность построения списка соседей оценивается [math] O(n^2)[/math]. Для каждой точки, после вычисления списка своих соседей, алгоритм рассматривает все пары его соседей. Для каждой пары точка вносит одну связь. Если процесс повторяется для каждой точки и счетчик ссылок увеличивается на единицу для каждой пары соседей, то в конце концов, ссылка рассчитывает на будут получены все пары точек. Если [math]m_i[/math] - число соседей точки [math]i[/math], тогда для нее мы должны увеличить количество связей на единицу [math]m_i^2[/math] раз. Таким образом, сложность алгоритма является [math]\sum m_i^2[/math] и может быть оценено [math] O(n m_m m_a)[/math]. Поскольку каждая точка [math]i[/math] может иметь не более [math]\min \{ m_m m_i, n \} )[/math] связей, то общие затраты памяти не превышают [math] O(\min \{ n m_m m_a, n^2 \} )[/math].
Построение каждой кучи потребует не более [math] O(n)[/math] времени (поскольку размер каждой кучи не может превышать [math] n [/math]) Сортировка каждой кучи потребует [math] O( n \log{} n)[/math]. Рассмотрим теперь основной while-цикл. Он содержит [math] O(n)[/math] итераций, где основная сложность каждого шага приходится на for-цикл. В худшем случае потребуется вставить новый кластер в [math] O(n)[/math] локальных куч размера [math] n[/math], что потребует [math] O( n \log{} n)[/math] времени. Таким образом, сложность всего внешнего цикла составляет [math] O(n^2 \log{} n)[/math] в худшем случае. Затраты памяти зависят от начального размера локальных куч, поскольку при слиянии кластеров их старые кучи удаляются, а размер новой не превышает суммы старых. Поскольку каждая куча сожержит лишь кластеры с ненулевыми связями, то сложность совпадает с первой частью и равна [math] O(\min \{ n m_m m_a, n^2 \} )[/math].
Итоговые оценки для всего алгоритма:
Сложность по времени:
- [math] O(n^2 + n m_m m_a + n^2 \log{} n)[/math]
Сложность по памяти:
- [math] O(\min \{ n^2, n m_m m_a \} )[/math]
Список обозначений:
- [math] m_a [/math] - среднее число соседей
- [math] m_m [/math] - максимальное число соседей
- [math]m_i[/math] - число соседей точки [math]i[/math]
- [math]n[/math] - размер входных данных
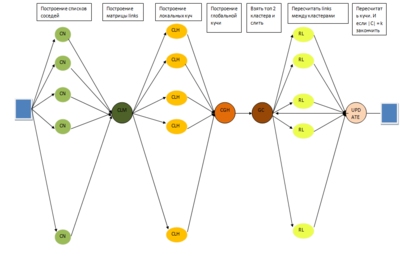
1.7 Информационный граф
Обозначения :
- CN - вершина построения соседей: заполнение nbrlist[i].
- CLM - вершина построения матрицы связей: заполнение link[i][j].
- CLH - вершина построения локальных куч: заполнение q[i].
- CGH - вершина построения глобальной кучи: заполнение Q.
- GC - вершина поиска и слияние топ 2 кластеров: построение w.
- RL - пересчет матрицы связей: заполнение link[x,w].
- UPDATE - Обновление глобальной кучи: обновление Q.
Как видно из графа в алгоритме есть ряд узких мест.
Рассмотрим их подробнее:
1) Вершина построения матрицы links. Данные вычисления не могут быть прямо распараллелены, нельзя для каждого списка соседей запустить данную функцию. Это связано с тем, что во время выполнения данных вычислений необходимо производить запись в матрицу и любой список может писать в любое место матрицы. В худшем случае (когда все соседи всем) при параллельном запуске возможны постоянные конфликты. Но в данной вершине все же есть потенциал для параллельной работы. Он заключается в том, что можно в параллели обрабатывать список соседей. При подходе в лоб нагрузка на ядра будет не равномерна.
Так же данный пункт можно реализовать иначе. Но затраты по памяти возрастут в N раз. Можно параллельно обрабатывать каждый вектор соседей. При среднем количестве соседей [math]m_a[/math] это займет [math]O(m_a ^ 2)[/math] операций (или если мы имеем [math]n^2[/math] ядер, то можно и за [math]O(m_a)[/math] + [math]O(log(n))[/math] для объединения N матриц.
2) Вершина построения глобальной кучи. В данной вершине необходимо добавить все вершины и после отсортировать в зависимости от наилучшего значения полезности каждой локальной кучи. Сортировку можно распараллелить.
3) Вершина взятия топ 2 кластеров. Узкая, но малозатратная вершина.
4) Вершина обновления куч. Так же узкая вершина в которой нужно в каждой локальной куче вставить в нужное место кластер и так же поступить с глобальной кучей.
1.8 Ресурс параллелизма алгоритма
Кроме нескольких узких мест алгоритма, которые не поддаются распараллеливанию, в целом алгоритм неплохо может быть переложен на параллельную архитектуру. Рассчитаем сложность алгоритма.
1) На первом этапе происходит вычисление соседей. Затраты данных операций при условии достаточного количества ядер [math]T_1 = O(n)[/math]
2) На этапе построения связей [math]n[/math] этапов в каждом из которых можно сделать [math]m[/math] расчетов(с учетом распараллеливания), где [math]m[/math] - количество соседей. В худшем случае [math]T_2 = O(n^2)[/math] в среднем случае [math]T_2 = O(n * m_a)[/math], где [math]m_a[/math] среднее ожидаемое число соседей.
3) Построение одной кучи это сложность [math]O(n)[/math]. Плюс для каждой кучи сортировка [math]O(n * log(n))[/math]. Соответственно итоговая сложность создания локальных куч [math]T_3 = O(n * log(n))[/math].
4) Построение и сортировка глобальной кучи так же [math]T_4 = O(n * log(n))[/math].
5) Цикл в котором происходит выбор кластеров, сливание, пересчет и обновление куч. Игнорируем выбор кластеров (достать из кучи [math]O(1)[/math] ). Для всех элементов кучи слитых кластеров пересчитываем значение связи, вставляем в кучу выбранного кластера информацию о новом кластере, удаляем старое. Делается это за [math]O(log(n))[/math]. Соответственно в худшем случае, одна итерация цикла это [math]T_i = O(log(n))[/math]. Количество итераций n - k. Значит
- [math]T_5 = O((n - k) * log(n))[/math]. При k = 1, [math]T_5 = O(n * log(n))[/math]
Итоговая сложность в худшем случае равна:
- [math]T_1 + T_2 + T_3 + T_4 + T_5 = O(n) + O(n^2) + O(n * log(n)) + O(n * log(n)) + O(n * log(n)) = O(n^2)[/math]
Итоговая сложность в среднем случае равна:
- [math]O(n * m_a) + O(n * log(n))[/math].
Тут важно понимать, что в зависимости от данных как [math]log(n)[/math] может быть больше [math]m_a[/math], так и наоборот.
Сложность по времени:
- [math]O(n * (m_a + log(n)))[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: Множество [math]S[/math] из [math]n[/math] элементов, число кластеров [math]k[/math]. В зависимости от реализации, некоторые параметры алгоритма могут также подаваться на вход или быть определены заранее.
Объем входных данных: Зависит от типа элементов из множества [math]S[/math], поскольку алгоритм может быть реализован для широкого класса данных. В общем случае требуется хранить массив из [math]n[/math] элементов.
Выходные данные: Метки класса (номер кластера) для каждого элемента.
Объем выходных данных: Для каждого входного элемента достаточно вернуть соответствующую ему метку (число), поэтому минимальный размер выхода: массив из [math]n[/math] чисел.
1.10 Свойства алгоритма
Алгоритм является детерминированным.
Алгоритм является устойчивым.
Вычислительная мощность алгоритма равна:
- [math]\frac{O(n^2 + n m_m m_a + n^2 \log{} n)}{n}[/math].
Отношение последовательной и параллельной сложности:
- [math]\frac{O(n^2 + n m_m m_a + n^2 \log{} n)}{O(n * (m_a + log(n)))}[/math].
К свойствам алгоритма можно отнести то, что сложность в среднем зависит от данных. Если растет среднее ожидаемое количество соседей, то растет и средняя сложность алгоритма. В худшем случае она может достигать [math]O(n^2)[/math] для данных с большой кучностью (одна большая плотная куча, где по факту 1 кластер). Но, если же среднее ожидаемое число соседей меньше [math]log(n)[/math], то сложность алгоритма будет [math]O(n *log(n))[/math]. В целом можно взять оценку [math]O(n * m_m)[/math], где [math] m_m [/math] максимальное количество соседей.
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
Как можно видеть из графа, представленного выше, в алгоритме есть 3 основных места для распараллеливания: 1) Составление матрицы связей 2) Построение локальных куч 3) Основной цикл алгоритма
Теоретическая оценка сложности алгоритма распараллеленного на p потоков:
- [math]O(\frac{n}{p}(n + m_m m_a + n\log{} n))[/math].
Соответственно: 1) При одинаковых входных данных, время работы обратно пропорционально количеству потоков. 2) При одинаковом количестве потоков, время зависит от входных данных кубически в худшем случае.
2.4.2 Масштабируемость реализации
Реализация алгоритма тестировалась на IBM pSeries 690 HPC Regatta.
- Максимальное количество потоков, способных работать в параллельном режиме: 16.
- Процессоры POWER4 1,3 ГГц; 16-процессорная архитектура SMP
Параметры запусков: 1) Запуски осуществлялись на задачах объемом 400, 800, 1600, 2400 точек. 2) Запуски осуществлялись на 1, 2, 4, 8, 16 потоках. 3) Количество кластеров = 2, [math]\theta[/math] = 0.3, соседями считались все точки в радиусе 0.3 .
| Количество потоков / Количество точек | 400 | 800 | 1200 | 1600 |
|---|---|---|---|---|
| 1 | 23 с. | 188 с. | 631 с. | 1514 с. |
| 2 | 17 с | 134 с | 452 с | 1079 с |
| 4 | 10 с | 79 с | 268 с | 631 с |
| 8 | 8 с | 45 с | 144 с | 342 с |
| 16 | 4 с | 24 с | 79 с | 185 с |
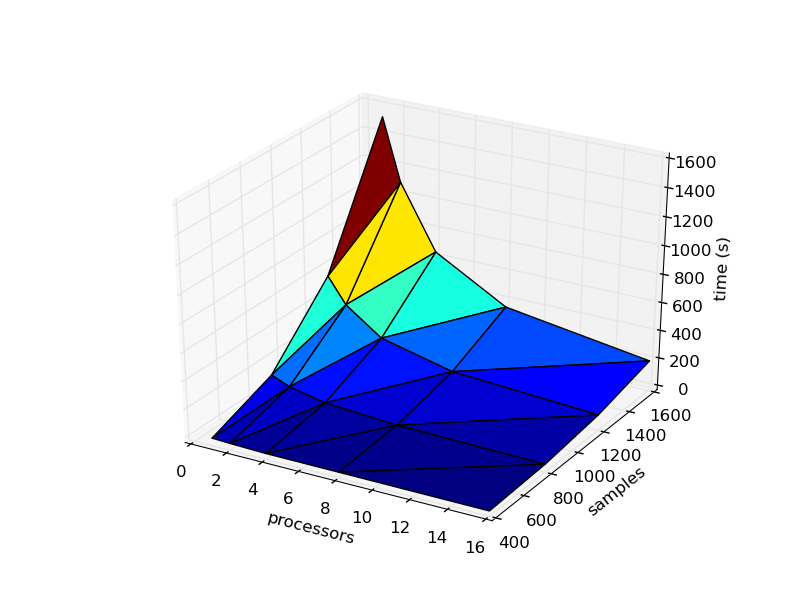
Как видно из таблицы, масштабируемость реализации коррелирует с теоретической оценкой.
Наглядно эти данные можно увидеть на следующем изображении.
Реализация доступна по ссылке на github [1]
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
feed4weka [2] - открытая библиотека, которая содержит различные алгоритмы для работы с данными.
3 Литература
1) ROCK: A Robust Clustering Algorithm for Categorical Attributes[3]
2) Data Mining Algorithms In R/Clustering/RockCluste [4]