Участница:Sannikovats/Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки (1): различия между версиями
м |
|||
| (не показаны 22 промежуточные версии 5 участников) | |||
| Строка 1: | Строка 1: | ||
| + | Основные авторы описания:[[Участница:Sannikovats| Санникова Татьяна Сергеевна]](п. 1.1-1.6),[[Участник:Plukshin| Лукшин Петр Андреевич]](п. 1.7-1.10, 2.4, 2.7). | ||
{{algorithm | {{algorithm | ||
| name = Вычисление определённого интеграла с использованием адаптивно сгущающейся сетки | | name = Вычисление определённого интеграла с использованием адаптивно сгущающейся сетки | ||
| − | + | | input_data = 1 функция,зависящая от 1 переменной, 3 числа ( точность ε и границы отрезка интегрирования[A,B]) | |
| − | + | | output_data = 1 число | |
| − | |||
| − | | input_data = | ||
| − | | output_data = | ||
}} | }} | ||
| − | |||
| − | |||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 14: | Строка 10: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Допустим, нам дана функция <math>f(x)</math> , определенная на отрезке, и возможность получать ее численное значение в любой из точек области определения за фиксированное время. Задача — вычислить определенный интеграл данной функции по заданной области и дать оценку погрешности вычисления.<br /> | + | Допустим, нам дана функция <math>f(x)</math> , определенная на отрезке, и возможность получать ее численное значение в любой из точек области определения за фиксированное время. Задача — вычислить определенный интеграл данной функции по заданной области и дать оценку погрешности вычисления.<br /> В случае, когда можно вычислить интеграл по формуле Ньютона-Лейбница, зная первообразную искомой функции, проблем не возникает. Однако, если первообразной нет, решение можно получить благодаря численным методам. Так определенному интегралу можно дать простую геометрическую интерпретацию - он равен площади криволинейной трапеции, ограниченной слева и справа вертикальными прямыми x=a, x=b, снизу - прямой y=0, а сверху – кривой y=f(x). |
| − | интегралу можно дать простую геометрическую интерпретацию - он равен площади криволинейной трапеции, ограниченной слева и справа вертикальными прямыми x=a, x=b, снизу - прямой y=0, а сверху – кривой y=f(x). | ||
Существуют различные последовательные методы построения адаптивных подвижных сеток, которые позволяют значительно повысить точность вычисления определенного интеграла за счет учета характера изменения подынтегральной функции. Представим общее описание для методов рекурсивного деления и локального стека. | Существуют различные последовательные методы построения адаптивных подвижных сеток, которые позволяют значительно повысить точность вычисления определенного интеграла за счет учета характера изменения подынтегральной функции. Представим общее описание для методов рекурсивного деления и локального стека. | ||
| Строка 33: | Строка 28: | ||
''Выходные данные:'' число, представляющее собой приближенное значение интеграла.<br /> | ''Выходные данные:'' число, представляющее собой приближенное значение интеграла.<br /> | ||
В качестве модельной задачи рассматривается проблема вычисления с точностью ε значения определенного интеграла <br /> | В качестве модельной задачи рассматривается проблема вычисления с точностью ε значения определенного интеграла <br /> | ||
| − | [[Файл: | + | [[Файл:1sann.jpg]] |
| − | + | ||
Пусть на отрезке <math> [A,B] </math> задана равномерная сетка, содержащая <math> n+1 </math> узел: | Пусть на отрезке <math> [A,B] </math> задана равномерная сетка, содержащая <math> n+1 </math> узел: | ||
| Строка 42: | Строка 37: | ||
<math> J_n(A,B)=\int_A^B{f(x)dx} = \frac{B - A}{n} \left( \frac{f(x_0)}{2} + \sum^{n-1}_{i=1} {f(x_i)} + \frac{f(x_n)}{2} \right)</math> | <math> J_n(A,B)=\int_A^B{f(x)dx} = \frac{B - A}{n} \left( \frac{f(x_0)}{2} + \sum^{n-1}_{i=1} {f(x_i)} + \frac{f(x_n)}{2} \right)</math> | ||
| − | [[Файл: 2sann.jpg]] [[Файл:3sann.jpg]] | + | [[Файл: 2sann.jpg]][[Файл:3sann.jpg]] |
Будем полагать значение <math> J </math> найденным с точностью <math> \epsilon </math>, если выполнено условие: | Будем полагать значение <math> J </math> найденным с точностью <math> \epsilon </math>, если выполнено условие: | ||
| Строка 65: | Строка 60: | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | В реализации алгоритма используется такая структура данных, как стек, в котором хранятся координаты концов отрезков | + | Как уже упоминалось в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть рассматриваемого метода составляют рекурсивные операции нахождения середины отрезка <math> C=(A+B)/2 </math>, вычисление значения функции в этой точке <math> fC=function(C)</math>, нахождение площадей трапеций, образованных после разбиение отрезка и их суммирование <math> sAC=(fA+fC)*(C-A)/2, sCB=(fC+fB)*(B-C)/2, sACB=sAC+sCB </math>, а также нахождение отношения модуля разности площади трапеции до разбиения отрезка и результату, полученному после разбиения, к сумме площадей после разбиения <math> |sAB - sACB|\leq \epsilon * |sACB| </math>, что обеспечивает проверку условия устойчивости.<br /> |
| + | |||
| + | |||
| + | === Схема реализации последовательного алгоритма === | ||
| + | В реализации алгоритма используется такая структура данных, как стек, в котором хранятся координаты концов отрезков: | ||
<source lang="cpp"> | <source lang="cpp"> | ||
//Данные, описывающие стек | //Данные, описывающие стек | ||
| Строка 109: | Строка 108: | ||
</source> | </source> | ||
| − | |||
// Заданная функция f(x) | // Заданная функция f(x) | ||
double f(double x); | double f(double x); | ||
| − | Рассмотрим функцию JLS, вычисляющую определенный интеграл от f(x) на [A,B] с заданной точностью | + | Рассмотрим функцию JLS, вычисляющую определенный интеграл от f(x) на [A,B] с заданной точностью eps методом локального стека, которая является вычислительным ядром алгоритма: |
<source lang="cpp"> | <source lang="cpp"> | ||
| + | //на вход функции подаются границы отрезка и точность | ||
int JLS(double A, double B, double eps) { | int JLS(double A, double B, double eps) { | ||
double J = 0;//значение интеграла | double J = 0;//значение интеграла | ||
| Строка 123: | Строка 122: | ||
double fC;//значение функции f(x)в середине отрезка [A,B] | double fC;//значение функции f(x)в середине отрезка [A,B] | ||
double sAB = (fA + fB)*(B - A)/2;//вычисление площади трапеции с основанием AB | double sAB = (fA + fB)*(B - A)/2;//вычисление площади трапеции с основанием AB | ||
| − | double sAC; | + | double sAC;//площадь трапеции с основанием AС |
| − | double sCB; | + | double sCB;//площадь трапеции с основанием СВ |
| − | double sACB; | + | double sACB;//сумма sAC и sCB |
| − | while(1) { | + | //бесконечный цикл с предусловием, прерывающийся при выполнении условия на порядок точности |
| + | while(1) { | ||
C = (A + B)/2;//середина отрезка | C = (A + B)/2;//середина отрезка | ||
fC = f(C); | fC = f(C); | ||
| Строка 132: | Строка 132: | ||
sCB = (fC + fB )*(B - C)/2; | sCB = (fC + fB )*(B - C)/2; | ||
sACB = sAC + sCB; | sACB = sAC + sCB; | ||
| + | //проверка выполнения условия на порядок точности: | ||
if(abs(sAB - sACB) >= eps*abs(sACB)) { | if(abs(sAB - sACB) >= eps*abs(sACB)) { | ||
PUT_INTO_STACK(A, C, fA, fC, sAC); | PUT_INTO_STACK(A, C, fA, fC, sAC); | ||
| Строка 149: | Строка 150: | ||
} | } | ||
</source> | </source> | ||
| + | В рамках этой функции поэтапно выполняются следующие операции: | ||
| + | #нахождение середины отрезка и значения функции в этой точке;<br /> | ||
| + | #вычисление частичных сумм на подобластях методом трапеций;<br /> | ||
| + | #определение выполнения условия точности: | ||
| + | #*если не выполняется, то продолжаем дробить область,"закладывая" в стек границы нового интервала (возвращение к пункту 2), | ||
| + | #*иначе добавляем к результату вычисленную сумму, завершая цикл. | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 167: | Строка 174: | ||
*взять один отрезок из глобального стека | *взять один отрезок из глобального стека | ||
*выполнить алгоритм локального стека, но,если при записи в локальный стек в нем есть несколько отрезков, а в глобальном стеке отрезки отсутствуют, то переместить часть отрезков из локального стека в глобальный стек | *выполнить алгоритм локального стека, но,если при записи в локальный стек в нем есть несколько отрезков, а в глобальном стеке отрезки отсутствуют, то переместить часть отрезков из локального стека в глобальный стек | ||
| − | * по исчерпании локального стека добавить полученную частичную сумму к общему значению интеграла. | + | * по исчерпании локального стека добавить полученную частичную сумму к общему значению интеграла. <br /> |
| + | [[Файл:Lukshin_01.png|1260px|thumb|left|Рис. Информационная структура алгоритма глобального стека]] <br /> | ||
| + | <br /> На рисунке изображена информационная структура алгоритма, на которой заметна его внутренняя цикличность. | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| − | + | Оценить параллельную сложность рассмотренного алгоритма является такой же невыполнимой задачей, как и оценка последовательной сложности. Рекурсивное деление областей интегрирования и поиск на них частичных сумм зависит непосредственно от конкретной функции и ее свойств. | |
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | + | ''Входные данные:'' заданная функция <math>f(x)</math>, определенная на отрезке <math>[A,B]</math>, заданная точность решения ε.<br /> | |
| + | ''Выходные данные:'' число, представляющее собой приближенное значение интеграла.<br /> | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | + | Рассмотренный алгоритм обладает свойством детерминированности, поскольку при определенных входных данных мы будем получать одинаковый результат. При этом он может адаптироваться в зависимости от сложности подынтегральной функции. | |
| − | + | Кроме того, алгоритм обладает внутренним параллелизмом, так как является численно устойчивым как в последовательной, так и в параллельной версиях. | |
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| − | + | === Особенности реализации последовательного алгоритма === | |
| + | === Локальность данных и вычислений === | ||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| − | + | === Динамические характеристики и эффективность реализации алгоритма === | |
| + | === Выводы для классов архитектур === | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
В настоящее время проблемой вычисления определенного графа на адаптивной сетке по нашим сведениям занимались только М.В. Якобовский и Е.Ю. Кулькова, рассматривавшие в своей работе "РЕШЕНИЕ ЗАДАЧ НА МНОГОПРОЦЕССОРНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ С РАЗДЕЛЯЕМОЙ ПАМЯТЬЮ" методы локального и глобального стеков. | В настоящее время проблемой вычисления определенного графа на адаптивной сетке по нашим сведениям занимались только М.В. Якобовский и Е.Ю. Кулькова, рассматривавшие в своей работе "РЕШЕНИЕ ЗАДАЧ НА МНОГОПРОЦЕССОРНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ С РАЗДЕЛЯЕМОЙ ПАМЯТЬЮ" методы локального и глобального стеков. | ||
| + | |||
| + | ==Литература== | ||
| + | #Якобовский М.В. | ||
| + | Введение в параллельные методы решения задач | ||
| + | #М.В. Якобовский и Е.Ю. Кулькова "РЕШЕНИЕ ЗАДАЧ НА МНОГОПРОЦЕССОРНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ С РАЗДЕЛЯЕМОЙ ПАМЯТЬЮ" | ||
Текущая версия на 10:27, 25 ноября 2016
Основные авторы описания: Санникова Татьяна Сергеевна(п. 1.1-1.6), Лукшин Петр Андреевич(п. 1.7-1.10, 2.4, 2.7).
| Вычисление определённого интеграла с использованием адаптивно сгущающейся сетки | |
| Последовательный алгоритм | |
| Объём входных данных | 1 функция,зависящая от 1 переменной, 3 числа ( точность ε и границы отрезка интегрирования[A,B]) |
| Объём выходных данных | 1 число |
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Допустим, нам дана функция [math]f(x)[/math] , определенная на отрезке, и возможность получать ее численное значение в любой из точек области определения за фиксированное время. Задача — вычислить определенный интеграл данной функции по заданной области и дать оценку погрешности вычисления.
В случае, когда можно вычислить интеграл по формуле Ньютона-Лейбница, зная первообразную искомой функции, проблем не возникает. Однако, если первообразной нет, решение можно получить благодаря численным методам. Так определенному интегралу можно дать простую геометрическую интерпретацию - он равен площади криволинейной трапеции, ограниченной слева и справа вертикальными прямыми x=a, x=b, снизу - прямой y=0, а сверху – кривой y=f(x).
Существуют различные последовательные методы построения адаптивных подвижных сеток, которые позволяют значительно повысить точность вычисления определенного интеграла за счет учета характера изменения подынтегральной функции. Представим общее описание для методов рекурсивного деления и локального стека.
1.1.1 Метод рекурсивного деления
Простейший из них - это метод рекурсивного деления, выигрыш от применения которого достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования. Интервал интегрирования разбивается на две части и независимо интегрируется функция [math]f(x)[/math] на каждой из них при соответствующих шагах интегрирования. Процедуру разбиения отрезков можно рекурсивно повторить до получения отрезков, на которых подынтегральная функция имеет простой вид и может быть аппроксимирована отрезком прямой с заданной точностью. Но при распараллеливании этого алгоритма (т.е. при запуске попарно подпрограмм, обрабатывающих половинки разбиваемого интервала) можно столкнуться со следующей проблемой: в реальной системе число процессоров ограничено и время, необходимое для порождения параллельных процессов существенно не равно нулю. А значит, запуск процессов, число которых значительно превышает число физических процессов системы при решении рассматриваемой задачи, приводит к увеличению времени ее решения по сравнению с последовательной программой. Основная сложность построения параллельного алгоритма на основе рассмотренного последовательного алгоритма, кроется в том, что, хотя несколько ветвей программы могли бы одновременно обрабатывать разные части интервала интегрирования, координаты концов этих отрезков хранятся в программном стеке процесса и фактически недоступны программисту. Если бы они были расположены в некотором явно описанном массиве, можно было бы передать их по частям для обработки разным нитям программы. Поэтому, необходимо рассмотреть метод локального стека, позволяющий распределить вычислительную работу между ограниченным числом процессов.
1.1.2 Метод локального стека
В основе этого алгоритма лежит описанный выше метод рекурсивного деления. Только данный метод использует массив данных, доступ к которым осуществляется по принципу стека - первым удаляется последний из добавленных элементов. В рассматриваемом алгоритме вместо стека можно было использовать и другие способы хранения заданий, например очередь. Стек выбран исключительно из соображений простоты реализации. Времена выполнения рассмотренных алгоритмов отличаются примерно на 5% в пользу локального стека, таким образом, алгоритм "локального стека" будем считать наилучшим из имеющихся в нашем распоряжении последовательных методов и на его примере построим дальнейшее описание.
1.2 Математическое описание алгоритма
Входные данные: заданная функция [math]f(x)[/math], определенная на отрезке [math][A,B][/math], заданная точность решения ε.
Выходные данные: число, представляющее собой приближенное значение интеграла.
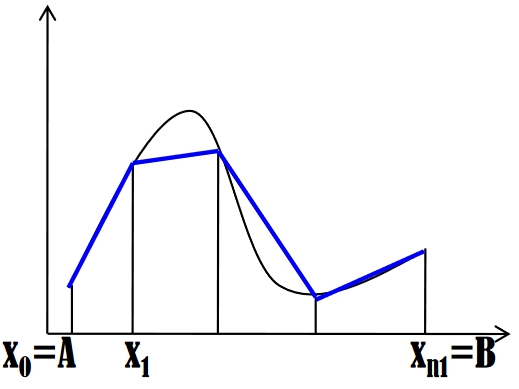
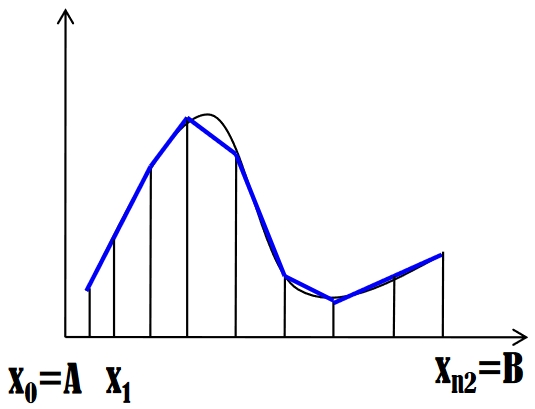
В качестве модельной задачи рассматривается проблема вычисления с точностью ε значения определенного интеграла
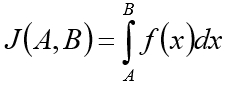
Пусть на отрезке [math] [A,B] [/math] задана равномерная сетка, содержащая [math] n+1 [/math] узел:
[math] x_{i} = A + \frac{(B - A)} {n} i, i = 0,...,n [/math]
Тогда, согласно методу трапеций, можно численно найти определенный интеграл от функции [math] f(x) [/math] на отрезке [math][A,B][/math]: [math] J_n(A,B)=\int_A^B{f(x)dx} = \frac{B - A}{n} \left( \frac{f(x_0)}{2} + \sum^{n-1}_{i=1} {f(x_i)} + \frac{f(x_n)}{2} \right)[/math]
Будем полагать значение [math] J [/math] найденным с точностью [math] \epsilon [/math], если выполнено условие:
[math] |J_{n_1} - J_{n_2}| \leq \epsilon |J_{n_2}|, n_1 \gt n_2, [/math] где [math] n_1 [/math] и [math] n_2 [/math] - количество узлов, образующих две разные сетки.
Используемые в алгоритме формулы:
- Из метода трапеций [math]sAB=\frac{f(A)+f(B)}{2}*(B-A)[/math]
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на:
- нахождение середины отрезка и значения функции в этой точке;
- вычисление частичных сумм на подобластях методом трапеций;
- определение выполнения условия точности:
- если не выполняется, то продолжаем дробить область,"закладывая" в стек границы нового интервала,
- иначе добавляем к результату вычисленную сумму, завершая цикл.
1.4 Макроструктура алгоритма
Как уже упоминалось в описании ядра алгоритма, основную часть рассматриваемого метода составляют рекурсивные операции нахождения середины отрезка [math] C=(A+B)/2 [/math], вычисление значения функции в этой точке [math] fC=function(C)[/math], нахождение площадей трапеций, образованных после разбиение отрезка и их суммирование [math] sAC=(fA+fC)*(C-A)/2, sCB=(fC+fB)*(B-C)/2, sACB=sAC+sCB [/math], а также нахождение отношения модуля разности площади трапеции до разбиения отрезка и результату, полученному после разбиения, к сумме площадей после разбиения [math] |sAB - sACB|\leq \epsilon * |sACB| [/math], что обеспечивает проверку условия устойчивости.
1.5 Схема реализации последовательного алгоритма
В реализации алгоритма используется такая структура данных, как стек, в котором хранятся координаты концов отрезков:
//Данные, описывающие стек
int sp = 0; // Указатель вершины стека
// Массив структур, в которых хранятся отложенные задания
struct mstk {
double A;//координата левой границы отрезка интегрирования
double B;//координата правой границы отрезка интегрирования
double fA;//значение функции на границе A
double fB;//значение функции на границе B
double s;//частичная сумма
} mstk[N];
В процедурах работы со стеком доступны следующие операции:
1)Проверка наличия элементов в стеке:
#define STACK_IS_NOT_FREE (sp > 0)
2)Операция "положить в стек":
#define PUT_INTO_STACK(A, B, fA, fB, s) {
mstk[sp].A = A;
mstk[sp].B = B;
mstk[sp].fA = fA;
mstk[sp].fB = fB;
mstk[sp].s = s;
++sp;
}
3)Операция "взять из стека верхний элемент":
#define GET_FROM_STACK(A, B, fA, fB, s) {
--sp;
A = mstk[sp].A;
B = mstk[sp].B;
fA = mstk[sp].fA;
fB = mstk[sp].fB;
s = mstk[sp].s;
}
// Заданная функция f(x)
double f(double x);
Рассмотрим функцию JLS, вычисляющую определенный интеграл от f(x) на [A,B] с заданной точностью eps методом локального стека, которая является вычислительным ядром алгоритма:
//на вход функции подаются границы отрезка и точность
int JLS(double A, double B, double eps) {
double J = 0;//значение интеграла
double fA = f(A);//значение функции f(x)на границе A
double fB = f(B);//значение функции f(x)на границе B
double C;//середина отрезка [A,B]
double fC;//значение функции f(x)в середине отрезка [A,B]
double sAB = (fA + fB)*(B - A)/2;//вычисление площади трапеции с основанием AB
double sAC;//площадь трапеции с основанием AС
double sCB;//площадь трапеции с основанием СВ
double sACB;//сумма sAC и sCB
//бесконечный цикл с предусловием, прерывающийся при выполнении условия на порядок точности
while(1) {
C = (A + B)/2;//середина отрезка
fC = f(C);
sAC = (fA + fC)*(C - A)/2;
sCB = (fC + fB )*(B - C)/2;
sACB = sAC + sCB;
//проверка выполнения условия на порядок точности:
if(abs(sAB - sACB) >= eps*abs(sACB)) {
PUT_INTO_STACK(A, C, fA, fC, sAC);
A = C;
fA = fC;
sAB = sCB;
}
else {
J += sACB;
if(STACK_IS_NOT_FREE) {
break;
}
GET_FROM_STACK(A, B, fA, fB, sAB);
}
}
return J;
}
В рамках этой функции поэтапно выполняются следующие операции:
- нахождение середины отрезка и значения функции в этой точке;
- вычисление частичных сумм на подобластях методом трапеций;
- определение выполнения условия точности:
- если не выполняется, то продолжаем дробить область,"закладывая" в стек границы нового интервала (возвращение к пункту 2),
- иначе добавляем к результату вычисленную сумму, завершая цикл.
1.6 Последовательная сложность алгоритма
Оценить аналитически последовательную сложность представленного алгоритма невозможно в силу того, что нельзя указать количество разбиений отрезка интегрирования для каждой отдельно взятой функции.
1.7 Информационный граф
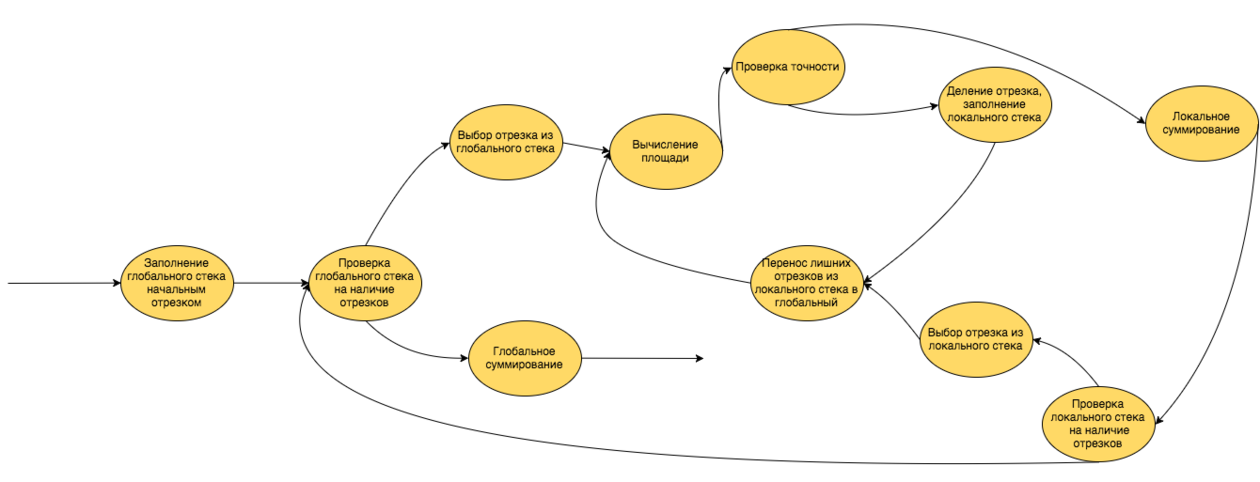
- Пусть есть доступный всем параллельным процессам список отрезков интегрирования,организованный в виде стека. Назовем его глобальным стеком.
- Пусть у каждого процесса есть свой, доступный только этому процессу локальный стек
- Перед запуском параллельных процессов в глобальный стек помещается единственная запись (в дальнейшем "отрезок"):
координаты концов отрезка интегрирования, значения функции на концах, приближенное значение интеграла на этом отрезке.
- Тогда, предлагается следующая схема алгоритма, выполняемого каждым из параллельных процессов:
Пока в глобальном стеке есть отрезки:
- взять один отрезок из глобального стека
- выполнить алгоритм локального стека, но,если при записи в локальный стек в нем есть несколько отрезков, а в глобальном стеке отрезки отсутствуют, то переместить часть отрезков из локального стека в глобальный стек
- по исчерпании локального стека добавить полученную частичную сумму к общему значению интеграла.
На рисунке изображена информационная структура алгоритма, на которой заметна его внутренняя цикличность.
1.8 Ресурс параллелизма алгоритма
Оценить параллельную сложность рассмотренного алгоритма является такой же невыполнимой задачей, как и оценка последовательной сложности. Рекурсивное деление областей интегрирования и поиск на них частичных сумм зависит непосредственно от конкретной функции и ее свойств.
1.9 Входные и выходные данные алгоритма
Входные данные: заданная функция [math]f(x)[/math], определенная на отрезке [math][A,B][/math], заданная точность решения ε.
Выходные данные: число, представляющее собой приближенное значение интеграла.
1.10 Свойства алгоритма
Рассмотренный алгоритм обладает свойством детерминированности, поскольку при определенных входных данных мы будем получать одинаковый результат. При этом он может адаптироваться в зависимости от сложности подынтегральной функции. Кроме того, алгоритм обладает внутренним параллелизмом, так как является численно устойчивым как в последовательной, так и в параллельной версиях.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
В настоящее время проблемой вычисления определенного графа на адаптивной сетке по нашим сведениям занимались только М.В. Якобовский и Е.Ю. Кулькова, рассматривавшие в своей работе "РЕШЕНИЕ ЗАДАЧ НА МНОГОПРОЦЕССОРНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ С РАЗДЕЛЯЕМОЙ ПАМЯТЬЮ" методы локального и глобального стеков.
3 Литература
- Якобовский М.В.
Введение в параллельные методы решения задач
- М.В. Якобовский и Е.Ю. Кулькова "РЕШЕНИЕ ЗАДАЧ НА МНОГОПРОЦЕССОРНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ С РАЗДЕЛЯЕМОЙ ПАМЯТЬЮ"