Нахождение суммы элементов массива сдваиванием: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
Konshin (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показано 14 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | {{level-a}} |
| + | |||
| + | Основные авторы описания: [[Участник:Frolov|А.В.Фролов]]. | ||
| + | |||
| + | == Свойства и структура алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| Строка 5: | Строка 9: | ||
'''Метод сдваивания''' используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового суммирования). Получил распространение благодаря как наименьшей из возможных высоте алгортима, так и из-за ряда своих вычислительных характеристик, а также (в среде нечисленных алгоритмов) из-за своей рекурсивности, то есть лёгкости записи. | '''Метод сдваивания''' используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового суммирования). Получил распространение благодаря как наименьшей из возможных высоте алгортима, так и из-за ряда своих вычислительных характеристик, а также (в среде нечисленных алгоритмов) из-за своей рекурсивности, то есть лёгкости записи. | ||
| − | === Математическое описание === | + | === Математическое описание алгоритма === |
Исходные данные: одномерный массив <math>n</math> чисел. | Исходные данные: одномерный массив <math>n</math> чисел. | ||
| Строка 15: | Строка 19: | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | Вычислительное ядро | + | Вычислительное ядро метода сдваивания для суммирования можно составить как из элементарных бинарных (всего <math>n - 1</math>) вычислений сумм, так и (рекуррентно) из набора реализаций метода сдваивания меньших размерностей. |
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| Строка 21: | Строка 25: | ||
Как уже записано в описании ядра алгоритма, основную часть метода составляют рекурсивные вызовы сумм массивов меньшей размерности. | Как уже записано в описании ядра алгоритма, основную часть метода составляют рекурсивные вызовы сумм массивов меньшей размерности. | ||
| − | === | + | === Схема реализации последовательного алгоритма === |
В своём чистом виде суммирование сдваиванием редко используют при последовательной реализации, поскольку при этом усложняется общая схема алгоритма и резко растёт потребность в памяти, нужной для хранения промежуточных данных. | В своём чистом виде суммирование сдваиванием редко используют при последовательной реализации, поскольку при этом усложняется общая схема алгоритма и резко растёт потребность в памяти, нужной для хранения промежуточных данных. | ||
| Строка 31: | Строка 35: | ||
=== Информационный граф === | === Информационный граф === | ||
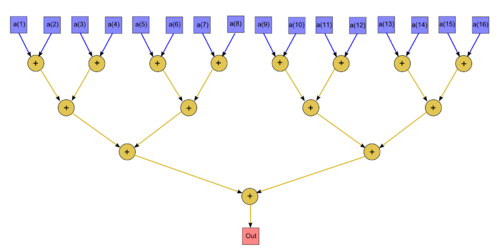
| − | + | На рис.1 изображён граф алгоритма. В данном случае выполнено суммирование 16 элементов массива. | |
| − | Вершины , соответствующие входным данным | + | Вершины, соответствующие входным данным, даны синим цветом, выходным данным - красным цветом. |
| − | [[file:binary-tree-based summation graph.png|center|thumb|500px|Суммирование массива методом сдваивания]] | + | [[file:binary-tree-based summation graph.png|center|thumb|500px|Рисунок 1. Суммирование массива методом сдваивания]] |
| − | === | + | === Ресурс параллелизма алгоритма === |
Для суммирования массива порядка <math>n</math> методом сдваивания в параллельном варианте требуется последовательно выполнить <math>\lceil \log_2 n \rceil</math> ярусов с убывающим (от <math>\frac{n}{2}</math> до <math>1</math>) количеством операций суммирования. | Для суммирования массива порядка <math>n</math> методом сдваивания в параллельном варианте требуется последовательно выполнить <math>\lceil \log_2 n \rceil</math> ярусов с убывающим (от <math>\frac{n}{2}</math> до <math>1</math>) количеством операций суммирования. | ||
При классификации по высоте ЯПФ, таким образом, метод сдваивания относится к алгоритмам с ''логарифмической сложностью''. При классификации по ширине ЯПФ его сложность будет ''линейной''. | При классификации по высоте ЯПФ, таким образом, метод сдваивания относится к алгоритмам с ''логарифмической сложностью''. При классификации по ширине ЯПФ его сложность будет ''линейной''. | ||
| − | === | + | === Входные и выходные данные алгоритма === |
Входные данные: массив <math>x</math> (элементы <math>x_i</math>). | Входные данные: массив <math>x</math> (элементы <math>x_i</math>). | ||
| Строка 57: | Строка 61: | ||
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является <math>\frac{n}{\log_2 n}</math> (отношение линейной к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего ''1 (входных и выходных данных столько же, сколько операций)''. При этом алгоритм полностью детерминирован. Дуги информационного графа нелокальны, от яруса к ярусу наблюдается показательный рост их длины, при любом размещении вершин графа. | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является <math>\frac{n}{\log_2 n}</math> (отношение линейной к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего ''1 (входных и выходных данных столько же, сколько операций)''. При этом алгоритм полностью детерминирован. Дуги информационного графа нелокальны, от яруса к ярусу наблюдается показательный рост их длины, при любом размещении вершин графа. | ||
| − | == Программная реализация == | + | == Программная реализация алгоритма == |
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | |||
| − | |||
| − | |||
| − | + | === Возможные способы и особенности параллельной реализации алгоритма === | |
| − | + | === Результаты прогонов === | |
| − | + | === Выводы для классов архитектур === | |
| − | |||
| − | ===== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Литература == | |
| − | + | <references /> | |
| − | + | [[Категория:Статьи в работе]] | |
| − | + | [[Категория:Метод сдваивания]] | |
| − | + | [[Категория:Векторные операции]] | |
| − | |||
| − | [[ | ||
| − | [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [ | + | [[En:Pairwise summation of numbers]] |
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 12:51, 8 июля 2022
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод сдваивания используется в качестве быстрого варианта вычисления длинных последовательностей ассоциативных операций (например, массового суммирования). Получил распространение благодаря как наименьшей из возможных высоте алгортима, так и из-за ряда своих вычислительных характеристик, а также (в среде нечисленных алгоритмов) из-за своей рекурсивности, то есть лёгкости записи.
1.2 Математическое описание алгоритма
Исходные данные: одномерный массив [math]n[/math] чисел.
Вычисляемые данные: сумма элементов массива.
Формулы метода: элементы на каждом этапе алгоритма разбиваются на пары. В каждой из пар находится сумма составляющих её элементов. На следующем этапе на пары разбиваются уже эти суммы (и те элементы, которые не вошли в уже вычисленные суммы), и т. д.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро метода сдваивания для суммирования можно составить как из элементарных бинарных (всего [math]n - 1[/math]) вычислений сумм, так и (рекуррентно) из набора реализаций метода сдваивания меньших размерностей.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть метода составляют рекурсивные вызовы сумм массивов меньшей размерности.
1.5 Схема реализации последовательного алгоритма
В своём чистом виде суммирование сдваиванием редко используют при последовательной реализации, поскольку при этом усложняется общая схема алгоритма и резко растёт потребность в памяти, нужной для хранения промежуточных данных.
1.6 Последовательная сложность алгоритма
Для вычисления суммы массива, состоящего из [math]N[/math] элементов, при любых разложениях [math]N[/math] на пары суть алгоритма сводится к простому переставлению скобок в формуле суммирования, и количество операций неизменно и равно [math]N - 1[/math]. Поэтому алгоритм должен быть отнесён к алгоритмам линейной сложности по количеству последовательных операций.
1.7 Информационный граф
На рис.1 изображён граф алгоритма. В данном случае выполнено суммирование 16 элементов массива. Вершины, соответствующие входным данным, даны синим цветом, выходным данным - красным цветом.
1.8 Ресурс параллелизма алгоритма
Для суммирования массива порядка [math]n[/math] методом сдваивания в параллельном варианте требуется последовательно выполнить [math]\lceil \log_2 n \rceil[/math] ярусов с убывающим (от [math]\frac{n}{2}[/math] до [math]1[/math]) количеством операций суммирования. При классификации по высоте ЯПФ, таким образом, метод сдваивания относится к алгоритмам с логарифмической сложностью. При классификации по ширине ЯПФ его сложность будет линейной.
1.9 Входные и выходные данные алгоритма
Входные данные: массив [math]x[/math] (элементы [math]x_i[/math]).
Дополнительные ограничения: отсутствуют.
Объём входных данных: [math]N[/math].
Выходные данные: сумма элементов массива.
Объём выходных данных: один скаляр.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является [math]\frac{n}{\log_2 n}[/math] (отношение линейной к логарифмической). При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных — всего-навсего 1 (входных и выходных данных столько же, сколько операций). При этом алгоритм полностью детерминирован. Дуги информационного графа нелокальны, от яруса к ярусу наблюдается показательный рост их длины, при любом размещении вершин графа.