Участник:Valeriya Shervarly/Ортогонализация Грама-Шмидта: различия между версиями
ASA (обсуждение | вклад) |
|||
| (не показано 10 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Авторы описания: Шерварлы В.Г. | |
= ЧАСТЬ. Свойства и структура алгоритмов = | = ЧАСТЬ. Свойства и структура алгоритмов = | ||
| Строка 5: | Строка 5: | ||
== Общее описание алгоритма == | == Общее описание алгоритма == | ||
| − | Процесс Грама-Шмидта - это алгоритм построения множества ортогональных (или ортонормированных) линейно-независимых векторов по исходному множеству векторов, при этом линейные оболочки получившегося и исходного множеств векторов совпадают. | + | Процесс Грама-Шмидта - это алгоритм построения множества ортогональных (или ортонормированных) линейно-независимых векторов по исходному множеству векторов, при этом линейные оболочки получившегося и исходного множеств векторов совпадают. Иными словами, построение ортогонального базиса из векторов, образующих произвольный базис. |
| − | Процесс Грама | + | Процесс Грама-Шмидта также можно рассматривать как разложение невырожденной квадратной матрицы в произведение унитарной (ортогональной) и верхнетреугольной матрицы с положительными диагональными элементами (QR-разложение). |
| − | Задача построения или вычисления ортогонального базиса некоторого линейного подпространства или пространства часто является подзадачей более крупных широко используемых задач, так что ортогонализация Грама-Шмидта является важным алгоритмом в линейной алгебре. | + | Задача построения или вычисления ортогонального базиса некоторого линейного подпространства или пространства часто является подзадачей более крупных широко используемых задач, так что ортогонализация Грама-Шмидта является важным и часто используемым алгоритмом в линейной алгебре. |
== Математическое описание алгоритма == | == Математическое описание алгоритма == | ||
| + | |||
| + | Процесс ортогонализации описывается следующей последовательностью формул: | ||
:: <math> | :: <math> | ||
| Строка 24: | Строка 26: | ||
где: | где: | ||
| − | <math>a_1, ..., a_n </math> - множество | + | <math>a_1, ..., a_n </math> - исходное множество линейно-независимых векторов |
<math>b_1, ..., b_n</math> - множество искомых векторов | <math>b_1, ..., b_n</math> - множество искомых векторов | ||
| Строка 31: | Строка 33: | ||
<math>\|b\| = \sqrt{<b,b>}</math> | <math>\|b\| = \sqrt{<b,b>}</math> | ||
| + | |||
== Вычислительное ядро алгоритма == | == Вычислительное ядро алгоритма == | ||
| − | Вычислительным ядром алгоритма является | + | Вычислительным ядром алгоритма является вычисление оператора проекции <math>proj_{b}a = \frac{<a, b>}{\|b\|^2} * b</math>. |
| + | |||
== Макроструктура алгоритма == | == Макроструктура алгоритма == | ||
| − | На уровне макроструктуры будем рассматривать <math>\frac{<a, b>}{\|b\|^2} * b</math> как отдельную макрооперацию <math>proj_{b}a</math> | + | На уровне макроструктуры будем рассматривать <math>\frac{<a, b>}{\|b\|^2} * b</math> как отдельную макрооперацию <math>proj_{b}a</math>. |
| + | |||
| + | Таким образом, на верхнем уровне алгоритм можно описать так (на каждом шаге выполняем вычисление очередного вектора итогового множества векторов): | ||
| + | |||
| + | '''Шаг 1''': | ||
| + | |||
| + | ::<math>b_1 = a_1</math> | ||
| + | |||
| + | '''Шаг i''' (i = 2, ..., n, где n - количество векторов): | ||
| + | |||
| + | ::<math>b_i = a_i - \sum^{i-1}_{k=1}{proj_{b_k}a_i}</math> | ||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
| − | + | Определим входные и выходные данные (два множества векторов, n - количество векторов в множестве): | |
| − | |||
| − | for | + | input: a = (a[1], ..., a[n]) |
| − | b[ | + | output: b = (b[1], ..., b[n]) |
| − | for k = 1,..., | + | |
| − | b[ | + | И далее последовательно находим каждый из векторов <math>b_i</math>, используя полученные на предыдущих итерациях цикла векторы <math>b_1, ..., b_{i-1}</math>: |
| + | |||
| + | b[1] = a[1] | ||
| + | for i = 2,...,n | ||
| + | b[i] = a[i] | ||
| + | Comment: во вложенном цикле вычисляем <math>b_i = a_i - \sum^{i-1}_{k=1}{proj_{b_k}a_i}</math> | ||
| + | for k = 1,...,i-1 | ||
| + | b[i] = b[i] - <a[i],b[k]>/<b[k],b[k]>*b[k] | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| − | + | Последовательная сложность алгоритма выражается следующими формулами | |
| + | (<math>n</math> - количество векторов, | ||
| + | <math>m</math> - количество компонент вектора): | ||
| + | |||
| + | * количество умножений: <math>\frac{3mn(n-1)}{2}</math> | ||
| + | |||
| + | * количество делений: <math>\frac{n(n-1)}{2}</math> | ||
| + | |||
| + | * количество сложений и вычитаний: <math>\frac{n(n-1)(2m - 1)}{2}</math> | ||
| + | |||
| + | Общая сложность алгоритма - <math>O(mn^2)</math> | ||
== Информационный граф == | == Информационный граф == | ||
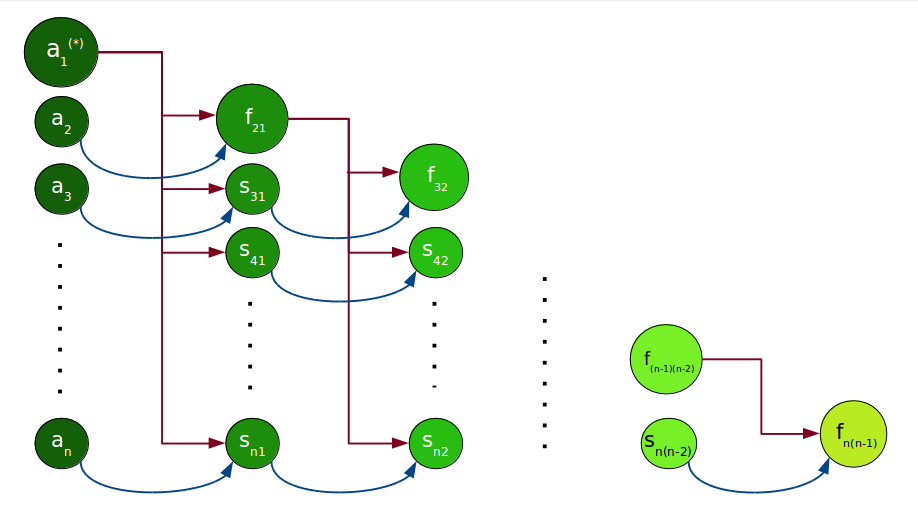
| + | Информационный граф алгоритма изображен на рисунке ниже. Используются следующие обозначения: | ||
| + | * <math>a_i, i=1, ..., n</math> - операции присваивания <math>b_i = a_i</math> | ||
| + | * <math>s_{ij} = b_i - proj_{b_j}a_i</math> | ||
| + | * <math>a_i^{(*)}</math> и <math>f_{ij}</math> отличаются от <math>a_i</math> и <math>s_{ij}</math> соответственно тем, что в этот момент завершается вычисление вектора <math>b_i</math>, являющегося и частью выходных данных, и необходимой информацией для последующего этапа. Так же в этих вершинах можно вычислять величину <math>\|b_i\|^2</math>, необходимую для вычисления соответствующих <math>proj_{b}a</math>. | ||
| + | * Разными оттенками зеленого цвета показана ярусно-параллельная форма графа алгоритма (вершины одного яруса выделены одним цветом). Высота ЯПФ - <math>n</math>, ширина ЯПФ - <math>n</math>. | ||
| + | |||
| + | [[Файл:CGS--infograph.png]] | ||
== Ресурс параллелизма алгоритма == | == Ресурс параллелизма алгоритма == | ||
Возможно параллельное вычисление всех <math>proj_{b_j}a_i, i=1,...n</math> для уже найденных <math>b_j</math> вместо вычисления каждого вектора <math>b_j</math> по очереди. Таким образом после каждой итерации будет получен один посчитанный вектор, необходимый для расчетов на следующей итерации. Однако степень распараллеливания будет падать на каждой итерации, что вместе с необходимостью синхронизации и многочисленными обменами информации может снизить эффективность распараллеливания. | Возможно параллельное вычисление всех <math>proj_{b_j}a_i, i=1,...n</math> для уже найденных <math>b_j</math> вместо вычисления каждого вектора <math>b_j</math> по очереди. Таким образом после каждой итерации будет получен один посчитанный вектор, необходимый для расчетов на следующей итерации. Однако степень распараллеливания будет падать на каждой итерации, что вместе с необходимостью синхронизации и многочисленными обменами информации может снизить эффективность распараллеливания. | ||
| + | |||
| + | Сложность параллельного варианта равна <math>O(nm)</math>, где <math>n</math> - количество векторов, <math>m</math> - количество компонент вектора. Можно сократить эту величину до <math>O(n\log{m})</math>, если еще параллельно проводить вычисление каждой макрооперации <math>proj_{b}a</math>, однако, опять же, не стоит забывать о расходах на синхронизацию и обмен информацией. | ||
| Строка 68: | Строка 107: | ||
'''Входные данные:''' | '''Входные данные:''' | ||
| − | N линейно независимых векторов (процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов, а также к линейно зависимым векторам. В последнем случае вектор <math>a_j</math> получится нулевым, если он зависит от векторов <math>a_1, ..., a_{j-1}</math>, и алгоритм должен сразу отбрасывать нулевые векторы) | + | N линейно независимых векторов (процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов, а также к линейно зависимым векторам. В последнем случае вектор <math>a_j</math> получится нулевым, если он зависит от векторов <math>a_1, ..., a_{j-1}</math>, и алгоритм должен сразу отбрасывать нулевые векторы). Объем входных данных: <math>mN</math>, где <math>N</math> - количество векторов, <math>m</math> - количество компонент вектора |
'''Выходные данные:''' | '''Выходные данные:''' | ||
| − | N ортогональных векторов, линейная оболочка которых совпадает с линейной оболочкой входного множества векторов. | + | N ортогональных векторов, линейная оболочка которых совпадает с линейной оболочкой входного множества векторов, объем выходных данных: <math>mN</math>. |
| + | == Свойства алгоритма == | ||
| − | + | Вычислительная мощность алгоритма: <math>O(n)</math>. Отношение последовательной сложности к параллельной - <math>\frac{mn^2}{mn}</math> <math>(</math>или <math>\frac{mn^2}{n\log{m}})</math>. | |
| − | + | Классический алгоритм (CGS) является численно-неустойчивым из-за частой потери ортогональности, вызванной ошибками округления в процессе вычислений. | |
| − | |||
| − | + | Существует модификации алгоритма Грама-Шмидта, которые являются более устойчивыми, например, модифицированный алгоритм Грама-Шмидта (MGS), блочные и итеративные варианты CGS и MGS. MGS численно эквивалентен методу Хаусхолдера QR-разложения, примененного к матрице, полученной из исходной путем добавления к ней сверху прямоугольной матрицы из нулевых элементов. | |
| + | Как можно видеть на изображении информационного графа алгоритма, существуют вершины с большой степенью исхода. Эти вершины соответствуют (в том числе) вычислению вектора <math>b_i</math> и результат этого вычисления должен быть сообщен всем вершинам, вычисляющим <math>proj_{b_i}a_j</math> для <math>j=1,..., n</math>. | ||
= ЧАСТЬ. Программная реализация алгоритма = | = ЧАСТЬ. Программная реализация алгоритма = | ||
| Строка 118: | Строка 158: | ||
GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}] | GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}] | ||
| − | * библиотека [https://github.com/fplll/fplll fplll] | + | * библиотека [https://github.com/fplll/fplll fplll] |
| − | * [http://numerics.mathdotnet.com/ Math.NET Numerics] | + | * [http://numerics.mathdotnet.com/ Math.NET Numerics] |
| − | * библиотека [https://www.nag.co.uk/ NAG] | + | * библиотека [https://www.nag.co.uk/ NAG] |
| − | * библиотека [https://www.mcs.anl.gov/petsc/documentation/index.html PETSc] | + | * библиотека [https://www.mcs.anl.gov/petsc/documentation/index.html PETSc] |
| Строка 130: | Строка 170: | ||
# https://ru.wikipedia.org/wiki/Процесс_Грама_―_Шмидта | # https://ru.wikipedia.org/wiki/Процесс_Грама_―_Шмидта | ||
| − | # | + | # Канатников А.Н., Крищенко А.П. "Линейная алгебра." |
| + | # Å. Björck. "Numerics of Gram-Schmidt orthogonalization" | ||
| + | # B. Milde, M. Schneider. "Parallel Implementation of Classical Gram-Schmidt Orthogonalization on CUDA Graphics Cards" | ||
Текущая версия на 14:30, 18 ноября 2016
Авторы описания: Шерварлы В.Г.
Содержание
- 1 ЧАСТЬ. Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 ЧАСТЬ. Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 ЧАСТЬ. Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Процесс Грама-Шмидта - это алгоритм построения множества ортогональных (или ортонормированных) линейно-независимых векторов по исходному множеству векторов, при этом линейные оболочки получившегося и исходного множеств векторов совпадают. Иными словами, построение ортогонального базиса из векторов, образующих произвольный базис.
Процесс Грама-Шмидта также можно рассматривать как разложение невырожденной квадратной матрицы в произведение унитарной (ортогональной) и верхнетреугольной матрицы с положительными диагональными элементами (QR-разложение).
Задача построения или вычисления ортогонального базиса некоторого линейного подпространства или пространства часто является подзадачей более крупных широко используемых задач, так что ортогонализация Грама-Шмидта является важным и часто используемым алгоритмом в линейной алгебре.
1.2 Математическое описание алгоритма
Процесс ортогонализации описывается следующей последовательностью формул:
- [math] \begin{align} b_1 & = a_1 \\ b_2 & = a_2 - \frac{\lt a_2, b_1\gt }{\|b_1\|^2} * b_1 \\ b_3 & = a_3 - \frac{\lt a_3, b_1\gt }{\|b_1\|^2} * b_1 - \frac{\lt a_3, b_2\gt }{\|b_2\|^2} * b_2 \\ ... \\ b_n & = a_n - \frac{\lt a_n, b_1\gt }{\|b_1\|^2} * b_1 - ... - \frac{\lt a_n, b_{n-1}\gt }{\|b_{n-1}\|^2} * b_{n-1} \\ \end{align} [/math]
где: [math]a_1, ..., a_n [/math] - исходное множество линейно-независимых векторов
[math]b_1, ..., b_n[/math] - множество искомых векторов
[math]\lt a,b\gt [/math] - скалярное произведение векторов
[math]\|b\| = \sqrt{\lt b,b\gt }[/math]
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является вычисление оператора проекции [math]proj_{b}a = \frac{\lt a, b\gt }{\|b\|^2} * b[/math].
1.4 Макроструктура алгоритма
На уровне макроструктуры будем рассматривать [math]\frac{\lt a, b\gt }{\|b\|^2} * b[/math] как отдельную макрооперацию [math]proj_{b}a[/math].
Таким образом, на верхнем уровне алгоритм можно описать так (на каждом шаге выполняем вычисление очередного вектора итогового множества векторов):
Шаг 1:
- [math]b_1 = a_1[/math]
Шаг i (i = 2, ..., n, где n - количество векторов):
- [math]b_i = a_i - \sum^{i-1}_{k=1}{proj_{b_k}a_i}[/math]
1.5 Схема реализации последовательного алгоритма
Определим входные и выходные данные (два множества векторов, n - количество векторов в множестве):
input: a = (a[1], ..., a[n]) output: b = (b[1], ..., b[n])
И далее последовательно находим каждый из векторов [math]b_i[/math], используя полученные на предыдущих итерациях цикла векторы [math]b_1, ..., b_{i-1}[/math]:
b[1] = a[1]
for i = 2,...,n
b[i] = a[i]
Comment: во вложенном цикле вычисляем [math]b_i = a_i - \sum^{i-1}_{k=1}{proj_{b_k}a_i}[/math]
for k = 1,...,i-1
b[i] = b[i] - <a[i],b[k]>/<b[k],b[k]>*b[k]
1.6 Последовательная сложность алгоритма
Последовательная сложность алгоритма выражается следующими формулами ([math]n[/math] - количество векторов, [math]m[/math] - количество компонент вектора):
- количество умножений: [math]\frac{3mn(n-1)}{2}[/math]
- количество делений: [math]\frac{n(n-1)}{2}[/math]
- количество сложений и вычитаний: [math]\frac{n(n-1)(2m - 1)}{2}[/math]
Общая сложность алгоритма - [math]O(mn^2)[/math]
1.7 Информационный граф
Информационный граф алгоритма изображен на рисунке ниже. Используются следующие обозначения:
- [math]a_i, i=1, ..., n[/math] - операции присваивания [math]b_i = a_i[/math]
- [math]s_{ij} = b_i - proj_{b_j}a_i[/math]
- [math]a_i^{(*)}[/math] и [math]f_{ij}[/math] отличаются от [math]a_i[/math] и [math]s_{ij}[/math] соответственно тем, что в этот момент завершается вычисление вектора [math]b_i[/math], являющегося и частью выходных данных, и необходимой информацией для последующего этапа. Так же в этих вершинах можно вычислять величину [math]\|b_i\|^2[/math], необходимую для вычисления соответствующих [math]proj_{b}a[/math].
- Разными оттенками зеленого цвета показана ярусно-параллельная форма графа алгоритма (вершины одного яруса выделены одним цветом). Высота ЯПФ - [math]n[/math], ширина ЯПФ - [math]n[/math].
1.8 Ресурс параллелизма алгоритма
Возможно параллельное вычисление всех [math]proj_{b_j}a_i, i=1,...n[/math] для уже найденных [math]b_j[/math] вместо вычисления каждого вектора [math]b_j[/math] по очереди. Таким образом после каждой итерации будет получен один посчитанный вектор, необходимый для расчетов на следующей итерации. Однако степень распараллеливания будет падать на каждой итерации, что вместе с необходимостью синхронизации и многочисленными обменами информации может снизить эффективность распараллеливания.
Сложность параллельного варианта равна [math]O(nm)[/math], где [math]n[/math] - количество векторов, [math]m[/math] - количество компонент вектора. Можно сократить эту величину до [math]O(n\log{m})[/math], если еще параллельно проводить вычисление каждой макрооперации [math]proj_{b}a[/math], однако, опять же, не стоит забывать о расходах на синхронизацию и обмен информацией.
1.9 Входные и выходные данные алгоритма
Входные данные: N линейно независимых векторов (процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов, а также к линейно зависимым векторам. В последнем случае вектор [math]a_j[/math] получится нулевым, если он зависит от векторов [math]a_1, ..., a_{j-1}[/math], и алгоритм должен сразу отбрасывать нулевые векторы). Объем входных данных: [math]mN[/math], где [math]N[/math] - количество векторов, [math]m[/math] - количество компонент вектора
Выходные данные: N ортогональных векторов, линейная оболочка которых совпадает с линейной оболочкой входного множества векторов, объем выходных данных: [math]mN[/math].
1.10 Свойства алгоритма
Вычислительная мощность алгоритма: [math]O(n)[/math]. Отношение последовательной сложности к параллельной - [math]\frac{mn^2}{mn}[/math] [math]([/math]или [math]\frac{mn^2}{n\log{m}})[/math].
Классический алгоритм (CGS) является численно-неустойчивым из-за частой потери ортогональности, вызванной ошибками округления в процессе вычислений.
Существует модификации алгоритма Грама-Шмидта, которые являются более устойчивыми, например, модифицированный алгоритм Грама-Шмидта (MGS), блочные и итеративные варианты CGS и MGS. MGS численно эквивалентен методу Хаусхолдера QR-разложения, примененного к матрице, полученной из исходной путем добавления к ней сверху прямоугольной матрицы из нулевых элементов.
Как можно видеть на изображении информационного графа алгоритма, существуют вершины с большой степенью исхода. Эти вершины соответствуют (в том числе) вычислению вектора [math]b_i[/math] и результат этого вычисления должен быть сообщен всем вершинам, вычисляющим [math]proj_{b_i}a_j[/math] для [math]j=1,..., n[/math].
2 ЧАСТЬ. Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- реализация для системы компьютерной алгебры maxima (GNU GPL)
load(eigen); x: matrix ([-2,1,0],[-2,0,1],[-0.5,-1,1]); y: gramschmidt(x);
- пример реализации для системы компьютерной алгебры mathematica (проприетарное программное обеспечение)
Projection[v1_, v2_] := (v1.v2*v2)/v2.v2
MultipleProjection[v1_, vecs_] := Plus @@ (Projection[v1, #1] &) /@ vecs
GramSchmidt[mat_] := Fold[Join[#1, {Normalize[#2 - MultipleProjection[#2, #1]]}] &, {}, mat]
GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}]
- библиотека fplll
- библиотека NAG
- библиотека PETSc
3 Литература
- https://ru.wikipedia.org/wiki/Процесс_Грама_―_Шмидта
- Канатников А.Н., Крищенко А.П. "Линейная алгебра."
- Å. Björck. "Numerics of Gram-Schmidt orthogonalization"
- B. Milde, M. Schneider. "Parallel Implementation of Classical Gram-Schmidt Orthogonalization on CUDA Graphics Cards"