Участник:Fokina/Рекурсивная координатная бисекция: различия между версиями
Fokina (обсуждение | вклад) |
Fokina (обсуждение | вклад) м |
||
| (не показано 13 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | {{Assignment}} | + | {{Assignment|ASA}} |
{{level-m}} | {{level-m}} | ||
{{algorithm | {{algorithm | ||
| name = Рекурсивная координатная бисекция | | name = Рекурсивная координатная бисекция | ||
| − | | serial_complexity = <math>O((k | + | | serial_complexity = <math>O(log(k)*n*log(n))</math> |
| pf_height = <math>O(log_2 k)</math> | | pf_height = <math>O(log_2 k)</math> | ||
| pf_width = <math>O(k/2)</math> | | pf_width = <math>O(k/2)</math> | ||
| − | | input_data = <math>n*m</math> | + | | input_data = <math>n*m + |E|</math> |
| output_data = <math>n*m</math> | | output_data = <math>n*m</math> | ||
}} | }} | ||
| − | + | Автор: [[U:Fokina|Фокина Н.Ю.]] | |
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 16: | Строка 16: | ||
Метод рекурсивной координатной бисекции был предложен Бергером (M. Berger) и Бохари (S. Bokhari) в 1987 году<ref>M. Berger and S. Bokhari. "A partitioning strategy for nonuniform problems on multiprocessors." IEEE Trans. Computers, C-36 (1987) 570-580.</ref> для решения задачи статической баланисировки загрузки. В основе метода лежит идея равномерного разбиения точек в пространстве с помощью гиперплоскостей. | Метод рекурсивной координатной бисекции был предложен Бергером (M. Berger) и Бохари (S. Bokhari) в 1987 году<ref>M. Berger and S. Bokhari. "A partitioning strategy for nonuniform problems on multiprocessors." IEEE Trans. Computers, C-36 (1987) 570-580.</ref> для решения задачи статической баланисировки загрузки. В основе метода лежит идея равномерного разбиения точек в пространстве с помощью гиперплоскостей. | ||
| − | На каждом этапе обрабатываемая область разбивается на две части, содержащие равное количество элементов. | + | На каждом этапе обрабатываемая область разбивается секущей плоскостью, перпендикулярной некоторой координатной оси, на две части, содержащие равное количество элементов. Чаще всего координатная ось выбирается таким образом, чтобы протяженность (разница координат по соответствующей оси самых крайних на ней точек) разрезаемой области вдоль этой оси была наибольшей. Возможны и другие способы, например, минимизация веса разрезанных ребер, в простейшем случае совпадающего с их числом. Для равномерных сеток оба приведенных выше критерия равнозначны. |
| − | Наиболее широко метод применяется при декомпозиции сеточных графов. В особенности полезен он при предварительном распределении по нескольким процессорам больших сеток, т.е. таких, описание которых не может быть полностью размещено в оперативной памяти одного процессорного узла. Это обусловлено высокой скоростью работы метода, его | + | Наиболее широко метод применяется при декомпозиции сеточных графов. В особенности полезен он при предварительном распределении по нескольким процессорам больших сеток, т.е. таких, описание которых не может быть полностью размещено в оперативной памяти одного процессорного узла. Это обусловлено высокой скоростью работы метода, его простотой и ориентированностью на распределенную обработку. |
| − | Наилучшие результаты метод демонстрирует на сетках, в которых вершины равномерно распределены по области простой формы. | + | Наилучшие результаты метод демонстрирует на сетках, в которых вершины равномерно распределены по области простой формы. Для этого вместо деления доменов пополам на каждом этапе требуется разбивать их таким образом, чтобы их размер был пропорционален итоговому количеству кластеров. |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
В начале работы имеется домен -- множество вершин графа <math>G</math>, заданных в виде векторов координат <math>(v_1,..,v_m)</math>, где <math>m</math> -- размерность пространства. | В начале работы имеется домен -- множество вершин графа <math>G</math>, заданных в виде векторов координат <math>(v_1,..,v_m)</math>, где <math>m</math> -- размерность пространства. | ||
| − | На каждой итерации осуществляется сортировка вершин, входящих в домен, вдоль оси, по которой он имеет наибольшую протяженность. Затем домен разделяется на поддомены путем разбиения: первые <math>n/2</math> или <math>n*k/ | + | На каждой итерации осуществляется сортировка вершин, входящих в домен, вдоль оси, по которой он имеет наибольшую протяженность. Затем домен разделяется на поддомены путем разбиения: первые <math>n/2</math> или <math>\frac{n*\frac{(k+1)}{2}}{k}</math> (<math>n</math> -- количество элементов в разбиваемом домене, <math>k</math> -- количество поддоменов, на который его требуется разбить) из отсортированного ранее домена относят к первому поддомену, оставшиеся -- к второму. Полученные поддомены также являются доменами и передаются в качестве входных данных на следующую итерацию до тек пор, пока общее количество поддоменов не достигнет первоначально заданного числа <math>k</math>. |
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| − | Основное время работы алгоритма приходится на сортировку данных на каждой итерации. В связи с этим целесообразно использовать алгоритмы сортировки, имеющие наименьшую среднюю сложность и показавшие высокую эффективность на практике. | + | Основное время работы алгоритма приходится на сортировку данных на каждой итерации. В связи с этим целесообразно использовать алгоритмы сортировки, имеющие наименьшую среднюю сложность и показавшие высокую эффективность на практике. Например, такой сортировкой может являться комбинация из пирамидальной сортировки и сортировки слиянием, имеющая сложность <math>O(n*\log(n))</math> <ref>Якобовский М.В. Параллельные алгоритмы сортировки больших объемов данных // Фундаментальные физико-математические проблемы и моделирование технико-технологических систем: Сб. науч. тр. : Янус-К, 2004, c. 235-249.</ref>. |
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| Строка 41: | Строка 41: | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
| − | Реализация метода рекурсивной бисекции в общем виде изображена на следующем рисунке: | + | Реализация метода рекурсивной бисекции на языке C в общем виде изображена на следующем рисунке: |
<source lang="c"> | <source lang="c"> | ||
void | void | ||
| Строка 62: | Строка 62: | ||
return; | return; | ||
}</source> | }</source> | ||
| + | В качестве входных параметров функция принимает массив вершин, содержащихся в текущем домене (<code>graph</code>), числа <code>n</code> -- количество вершин, <code>k</code> -- количество поддоменов, на который требуется разбить данный домен. | ||
| + | |||
| + | В теле функции вычисляется отношение между количеством поддоменов, на которые будут впоследствии разбиты полученные на текущей итерации поддомены (<code>k1</code> и <code>k2</code>), и размеры поддоменов, которые будут получены на данной итерации (<code>n1</code> и <code>n2</code>). С помощью вызова функции <code>bisect</code> осуществляется непосредственно разбиение на два поддомена. Затем функция <code>recursive_bisect</code> рекурсивно вызывается на полученных поддоменах до тех пор, пока остается необходимость в дальнейшем их разбиении. | ||
Выбор конкретного алгоритма зависит от использованной функции <code>bisect</code>, которой осуществляется разбиение вершин на два подграфа на каждом из этапов. В случае координатной бисекции она имеет следующий вид: | Выбор конкретного алгоритма зависит от использованной функции <code>bisect</code>, которой осуществляется разбиение вершин на два подграфа на каждом из этапов. В случае координатной бисекции она имеет следующий вид: | ||
| Строка 81: | Строка 84: | ||
return; | return; | ||
}</source> | }</source> | ||
| + | Входными параметрами функции являются массив вершин в домене, его размер, а также размеры полученных в результате разбиения поддоменов. Выходными параметрами являются массивы вершин, входящих в полученные поддомены. Следует отметить, что на вход достаточно передавать размер лишь одного из поддоменов, например, первого, поскольку размер второго явно из него следует, т.к. <math>n1 + n2 == n</math>. В данном примере оба размера передаются для наглядности и единообразия. | ||
| + | |||
| + | В процессе работы функции с помощью вызова функции <code>calculate_max_distance</code> выбирается координатная ось, вдоль которой сетка имеет наибольшую протяженность. Затем вершины сортируются вдоль этой оси, и создаются два поддомена: в первый входят вершины с индексами <code>[0..n1)</code> в отсортированном массиве, в второй -- <code>[n1..n)</code>, где <code>n1</code> равно <math>\frac{n*\frac{(k+1)}{2}}{k}</math>. | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 88: | Строка 94: | ||
# Сортировка. Наиболее эффективным алгоритмом последовательной сортировки является комбинация сортировки слиянием и пирамидальной сортировки <ref>Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2</ref>. Сложность как пирамидальной сортировки, так и сортировки слиянием оценивается как <math>O(nlog_2(n))</math>. | # Сортировка. Наиболее эффективным алгоритмом последовательной сортировки является комбинация сортировки слиянием и пирамидальной сортировки <ref>Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2</ref>. Сложность как пирамидальной сортировки, так и сортировки слиянием оценивается как <math>O(nlog_2(n))</math>. | ||
# Разбиение домена на поддомены осуществляется за <math>O(1)</math>. | # Разбиение домена на поддомены осуществляется за <math>O(1)</math>. | ||
| − | Исходя из этого, общая сложность каждой итерации оценивается сверху как <math>O(nlog_2(n))</math>, а их количество составляет <math> | + | Исходя из этого, общая сложность каждой итерации оценивается сверху как <math>O(nlog_2(n))</math>, а их количество составляет <math>\lceil log_2{k} \rceil</math>. Таким образом, последовательная сложность метода -- <math>O(log(k)*n*log(n))</math>. |
=== Информационный граф === | === Информационный граф === | ||
| Строка 97: | Строка 103: | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| − | При разбиении графа на <math>k</math> подграфов глубина рекурсии составляет <math>\lceil log_2 k \rceil</math>, а на каждом <math>i</math> шаге решается до <math>2^i</math> подзадач. Поскольку подзадачи, возникающие на каждом шаге рекурсии, не имеют информационных зависимостей | + | При разбиении графа на <math>k</math> подграфов глубина рекурсии составляет <math>\lceil log_2 k \rceil</math>, а на каждом <math>i</math> шаге решается до <math>2^i</math> подзадач. Поскольку подзадачи, возникающие на каждом шаге рекурсии, не имеют между собой информационных зависимостей, их решение можно распараллелить, получив таким образом некоторый прирост производительности. Исходя из того, что сложность этих подзадач примерно одинакова, можно считать, что |
| − | их решение занимает примерно одинаковое время <math>t</math> | + | их решение занимает на каждом ярусе примерно одинаковое время <math>t</math>. Пусть доступно бесконечное число одинаковых процессоров. Тогда на каждом ярусе размер входного массива равен <math>\frac{n}{2^i}</math>, где <math>n</math> -- исходное количество вершин, <math>i</math> -- номер яруса. При использовании сортировки сложностью <math>O(n*log(n))</math> итоговую сложность можно вычислить как <math>O(\sum\limits_{i=0}^{\lceil log_2 k \rceil}\frac{n}{2^i}*\log_2{\frac{n}{2^i}})= |
| + | O(\sum\limits_{i=0}^{\lceil log_2 k \rceil}(n*\frac{(\log_2{n} - \log_2{2^i})}{2^i}))=</math> | ||
| − | + | <math>O(\sum\limits_{i=0}^{\lceil log_2 k \rceil}(n*\frac{(\log_2{n} - i)}{2^i}))=</math> | |
| − | <math> | + | <math> |
| + | O(n*(\sum\limits_{i=0}^{\lceil log_2 k \rceil}(\frac{log_2{n}}{2^i})-\sum\limits_{i=0}^{\lceil log_2 k \rceil}(\frac{i}{2^i})))= | ||
| + | O(n*(\log_2{n} - 1))=O(n*\log_2{n})-O(n)=</math> | ||
| + | <math>O(n*\log_2{n})</math>. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | Метод рекурсивной координатной бисекции работает над графами, часто -- сеточными. | + | Метод рекурсивной координатной бисекции работает над графами, часто -- сеточными. Входные данные удобно задавать в виде массива координат в <math>n</math>-мерном прострастве, т.е. векторов размерности <math>n</math>. Как правило, в прикладных задачах <math>n</math> составляет 2 или 3, т.е. заданы координаты на плоскости или в пространстве. |
| − | '''Входные данные алгоритма:''' Исходный граф <math>G</math>, натуральное число <math> k \in \N </math> -- количество подграфов, на которое нужно осуществить разбиение. | + | '''Входные данные алгоритма:''' Исходный граф <math>G = (V, E)</math>, натуральное число <math> k \in \N </math> -- количество подграфов, на которое нужно осуществить разбиение. |
| − | '''Объем входных данных:''' <math>n*m</math>, где <math>n</math> -- количество векторов, <math>m</math> -- размерность пространства. | + | '''Объем входных данных:''' <math>n*m + |E|</math>, где <math>n</math> -- количество векторов, <math>m</math> -- размерность пространства, <math>E</math> -- ребра в графе. Для равномерных сеток связи между вершинами можно не учитывать, т.е. |
| + | объем входных данных можно ограничить <math>n*m</math>. | ||
'''Выходные данные алгоритма:''' Множество <math>G_1 .. G_k</math> подграфов исходного графа <math>G</math>. | '''Выходные данные алгоритма:''' Множество <math>G_1 .. G_k</math> подграфов исходного графа <math>G</math>. | ||
| Строка 115: | Строка 126: | ||
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | Метод рекурсивной координатной бисекции является устойчивым и детерминированным. Его вычислительная мощность пропорциональна <math>log( | + | Метод рекурсивной координатной бисекции является устойчивым и детерминированным. |
| + | Его вычислительная мощность пропорциональна <math>log(k)</math> (отношение последовательной | ||
| + | сложности <math>O(log(k)*n*log(n))</math> к параллельной <math>O(n*log(n))</math>). | ||
Можно также отметить следующие особенности метода: | Можно также отметить следующие особенности метода: | ||
* Использование параллельного алгоритма рекурсивной координатной бисекции целесообразно при разбиении на большое число подграфов. | * Использование параллельного алгоритма рекурсивной координатной бисекции целесообразно при разбиении на большое число подграфов. | ||
| − | * Наибольшее ускорение достигается при разбиении на число подграфов, | + | * Наибольшее ускорение достигается при разбиении на число подграфов, являющемся степенью двойки. |
* Наибольшее ускорение достигается при использовании числа процессоров, являющегося степенью двойки. | * Наибольшее ускорение достигается при использовании числа процессоров, являющегося степенью двойки. | ||
| Строка 134: | Строка 147: | ||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| − | + | Масштабируемость алгоритма была исследована на примере реализации метода рекурсивной координатной бисекции, содержащейся в библиотеке ZOLTAN v3.83 [http://www.cs.sandia.gov/zoltan/] (файл example/C/simpleRCB.c). В части испытаний использованная программа была модифицирована таким образом, чтобы фиксировать количество поддоменов, на которое требуется разбить сетку. Для этого в функцию, непосредственно осуществляющую бисекцию <code>Zoltan_LB_Partition()</code>, был дополнительно передан параметр <code>NUM_GLOBAL_PARTS</code> (часть контекста <code>struct Zoltan_Struct *zz</code>). | |
| − | + | ||
| + | В качестве тестового стенда было использовано ЭВМ BlueGene/P ВМК МГУ. | ||
| + | Первый этап тестирования выполнялся в соответствии с методикой испытаний: | ||
| + | *фиксировано значение параметра <math>k</math> -- итоговое количество поддоменов (16); | ||
| + | *в качестве тестового набора входных данных была сгенерирована двумерная регулярная сетка размера <math>N*N</math>, где <math>N</math> -- 1024, 2048, 3072, 4096, 5120. | ||
| + | *для каждого размера сетки выполнена серия запусков на различном количестве процессоров: 1, 2, 4, [8..128] c шагом 8 (8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 128). | ||
| + | |||
| + | Тестовая программа и сама библиотека ZOLTAN были скомпилированы с помощью <code>mpicc 1.1 (gcc 4.1.2)</code>, параметры компиляции стандартные, приведены в <code>Makefile/make everything</code>. Для запуска использовался скрипт, одновременно ставящий в очередь все задачи с одинаковым размером входной сетки. Пример запуска одной задачи: <code>mpisubmit.bg -n $3 --stdout result_$2_$1_$3.txt -w 00:15:00 simpleRCB.exe -- mesh$1.txt $2 $1</code>; <code>$1</code> -- размер сетки, <code>$2</code> -- количество поддоменов, <code>$3</code> -- количество процессоров. | ||
| + | |||
| + | Полученные результаты замеров времени работы показаны на рис. 3 и 4. На рис. 4 для наглядности использована логарифмическая шкала для количества процессоров, а также исключены результаты для запусков при количестве процессоров, не являющемся степенью 2. Соответствующие им результаты эффективности распараллеливания приведены на рис. 5 и 6. | ||
| + | |||
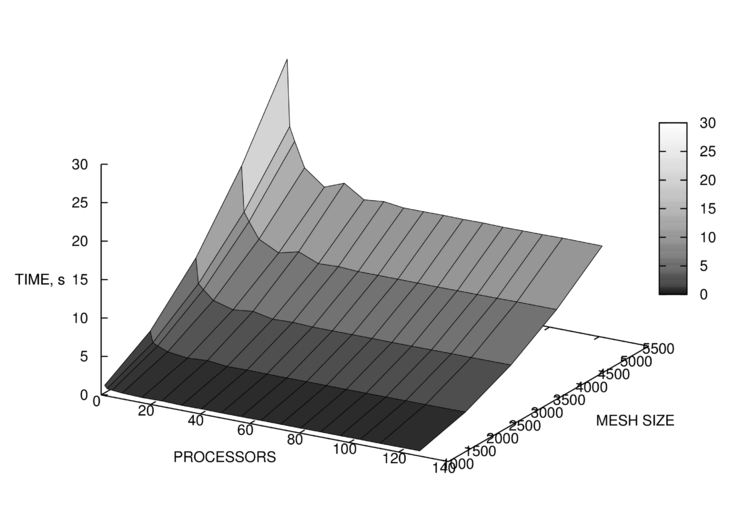
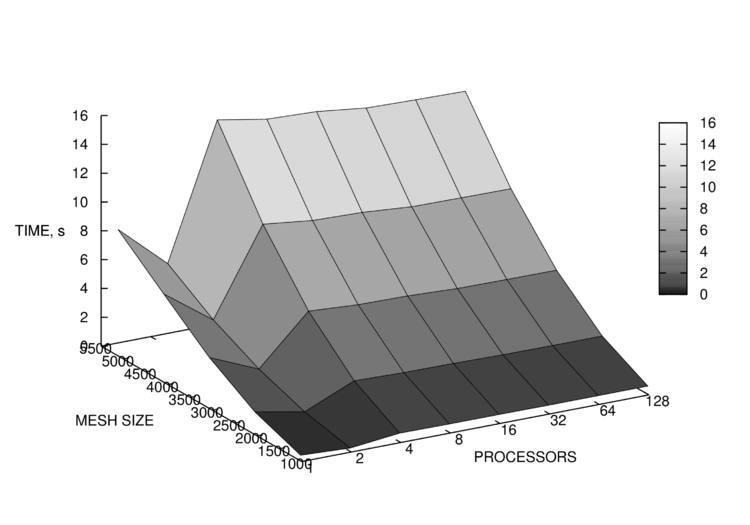
| + | [[File:Plot16.png|750px|thumb|center|Рис. 3. Время работы алгоритма в зависимости от числа процессоров и размера сетки]] | ||
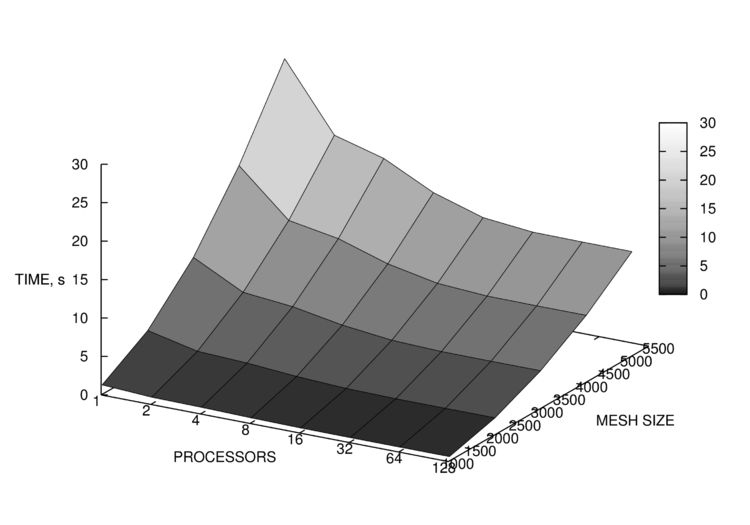
| + | [[File:Plot16_1.png|750px|thumb|center|Рис. 4. Время работы алгоритма в зависимости от числа процессоров и размера сетки (упрощенно)]] | ||
| + | |||
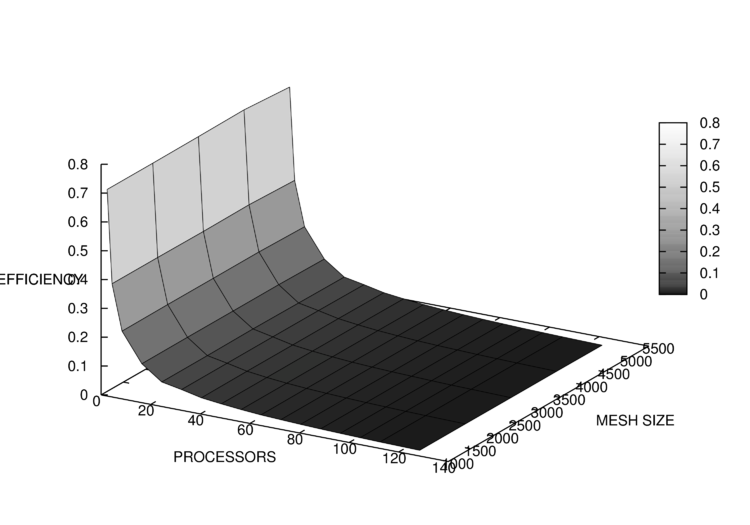
| + | [[File:Efficiency16.png|750px|thumb|center|Рис. 5. Эффективность распараллеливания алгоритма в зависимости от числа процессоров и размера сетки]] | ||
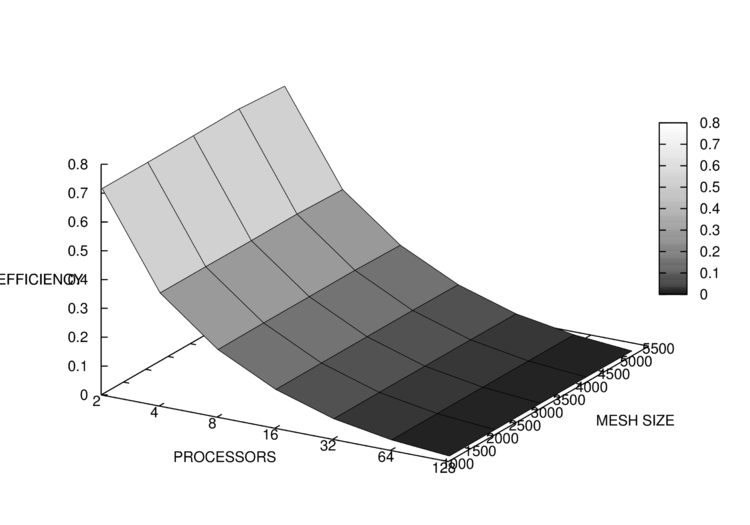
| + | [[File:Efficiency16_1.png|750px|thumb|center|Рис. 6. Эффективность распараллеливания алгоритма в зависимости от числа процессоров и размера сетки (упрощенно)]] | ||
| + | |||
| + | По мере увеличения количества процессоров масштабируемость по данным стремится к линейной. | ||
| + | |||
| + | Минимальное значение эффективности распараллеливания составило 0.017 (сетка 1024*1024, 128 процессоров), максимальное -- 0.717 (сетка 4096*4096, 2 процессора). | ||
| + | |||
| + | На рис. 3 было обнаружено небольшое увеличение производительности алгоритма при количестве процессоров, равном количеству поддоменов, на которое требовалось разбить сетку (16). Это обусловлено тем, что в случае совпадения количества поддоменов и процессоров, количество вершин, приходящихся на каждый из процессоров в течение обработки, оптимально. В связи с этим было проведено дополнительное исследование производительности алгоритма в таком режиме, т.е. при всех запусках итоговое количество поддоменов совпадало с количеством используемых процессоров. Такое использование характерно для решения задачи балансировки нагрузки, а также предварительного разбиения вершин сетки по процессорам, для чего обычно и используется рекурсивная координатная бисекция. Результат тестирования приведен на рис. 7. | ||
| + | |||
| + | [[File:Plot_.png|750px|thumb|center|Рис. 7. Время работы алгоритма в зависимости от числа процессора и размера сетки, количество поддоменов совпадает с количеством процессоров]] | ||
| + | |||
| + | На графике наблюдается существенное увеличение производительности при числе процессоров, равном 2, что обусловлено наименьшими затратами на передачу данных. Дальнейшее увеличение числа процессоров (и, одновременно, поддоменов) приводит к одинаковому результату, худшему, чем в случае двух процессоров. | ||
| + | |||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| − | Наиболее широко в настоящее время применяется параллельный алгоритм рекурсивной координатной бисекции, реализованный в пакете ZOLTAN (Zoltan2) [https://trilinos.org/docs/dev/packages/zoltan2/doc/html/rcbPage.html]. | + | Наиболее широко в настоящее время применяется параллельный алгоритм рекурсивной координатной бисекции, реализованный в пакете ZOLTAN (Zoltan2) [https://trilinos.org/docs/dev/packages/zoltan2/doc/html/rcbPage.html]. Он может разбивать поддомены двумя способами: |
| + | * BISECTION -- выбирается кандидат из отрезка [L, R], чье значение ближе всего к (L+R)/2. | ||
| + | * RANDOM -- выбирается первый кандидат -- медиана коллекции локальных медиан каждого процесса. Затем осуществляется бинарный поиск по оставшимся локальным медианам. Если медиана все еще не найдена, каждуй процесс предоставляет кандидата, выбранного случайным образом из значений в интересующей области, и бинарный поиск производится среди них. Последний шаг повторяется на сужаемой описанным выше образом области до тех пор, пока медиана не будет найдена. | ||
| + | |||
| + | Для осуществления разрезов области не пересортируются, а используют древовидную структуру, хранящую | ||
| + | информацию о ранее произведенных разрезах. Весь массив исходных данных хранится распределенным по нескольким | ||
| + | процессорам. | ||
Метод рекурсивной координатной бисекции сеток реализован в пакете GridSpiderPar [http://lira.imamod.ru/FondProgramm/Decomposition/]. | Метод рекурсивной координатной бисекции сеток реализован в пакете GridSpiderPar [http://lira.imamod.ru/FondProgramm/Decomposition/]. | ||
Текущая версия на 19:37, 6 февраля 2017
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 06.02.2017 Данная работа соответствует формальным критериям. Проверено ASA. |
| Рекурсивная координатная бисекция | |
| Последовательный алгоритм | |
| Последовательная сложность | O(log(k)*n*log(n)) |
| Объём входных данных | n*m + |E| |
| Объём выходных данных | n*m |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(log_2 k) |
| Ширина ярусно-параллельной формы | O(k/2) |
Автор: Фокина Н.Ю.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод рекурсивной координатной бисекции был предложен Бергером (M. Berger) и Бохари (S. Bokhari) в 1987 году[1] для решения задачи статической баланисировки загрузки. В основе метода лежит идея равномерного разбиения точек в пространстве с помощью гиперплоскостей.
На каждом этапе обрабатываемая область разбивается секущей плоскостью, перпендикулярной некоторой координатной оси, на две части, содержащие равное количество элементов. Чаще всего координатная ось выбирается таким образом, чтобы протяженность (разница координат по соответствующей оси самых крайних на ней точек) разрезаемой области вдоль этой оси была наибольшей. Возможны и другие способы, например, минимизация веса разрезанных ребер, в простейшем случае совпадающего с их числом. Для равномерных сеток оба приведенных выше критерия равнозначны.
Наиболее широко метод применяется при декомпозиции сеточных графов. В особенности полезен он при предварительном распределении по нескольким процессорам больших сеток, т.е. таких, описание которых не может быть полностью размещено в оперативной памяти одного процессорного узла. Это обусловлено высокой скоростью работы метода, его простотой и ориентированностью на распределенную обработку.
Наилучшие результаты метод демонстрирует на сетках, в которых вершины равномерно распределены по области простой формы. Для этого вместо деления доменов пополам на каждом этапе требуется разбивать их таким образом, чтобы их размер был пропорционален итоговому количеству кластеров.
1.2 Математическое описание алгоритма
В начале работы имеется домен -- множество вершин графа G, заданных в виде векторов координат (v_1,..,v_m), где m -- размерность пространства. На каждой итерации осуществляется сортировка вершин, входящих в домен, вдоль оси, по которой он имеет наибольшую протяженность. Затем домен разделяется на поддомены путем разбиения: первые n/2 или \frac{n*\frac{(k+1)}{2}}{k} (n -- количество элементов в разбиваемом домене, k -- количество поддоменов, на который его требуется разбить) из отсортированного ранее домена относят к первому поддомену, оставшиеся -- к второму. Полученные поддомены также являются доменами и передаются в качестве входных данных на следующую итерацию до тек пор, пока общее количество поддоменов не достигнет первоначально заданного числа k.
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на сортировку данных на каждой итерации. В связи с этим целесообразно использовать алгоритмы сортировки, имеющие наименьшую среднюю сложность и показавшие высокую эффективность на практике. Например, такой сортировкой может являться комбинация из пирамидальной сортировки и сортировки слиянием, имеющая сложность O(n*\log(n)) [2].
1.4 Макроструктура алгоритма
Массив данных, используемый при рекурсивной координатной бисекции, содержит в себе наборы данных о каждой вершине, включающие координаты и номер вершины.
На каждом этапе рекурсивной координатной бисекции происходит следующее:
- Определяются границы наименьшего параллелепипеда, охватывающего все вершины, которые делятся на данном этапе. Вычисляются максимумы по каждой из координат. Определяется координата j, вдоль которой параллелепипед имеет наибольшую протяженность.
- Выполняется сортировка вершин по координате j.
- Создается два новых поддомена. Первая половина вершин из отсортированного домена помещается в первый поддомен, все последующие -- в второй.
Стоит отметить, что разбиение целесообразно производить одновременно по нескольким координатам. Для этого вершины сортируются сначала по одной координате, потом внутри нее по следующей координате в циклическом порядке и т.д., что позволяет обрабатывать ситуации наличия нескольких узлов с одним значением координаты. В результате медиана проводится точно, и в разбиении на равные домены числа вершин в доменах отличаются не больше чем на единицу[3].
1.5 Схема реализации последовательного алгоритма
Реализация метода рекурсивной бисекции на языке C в общем виде изображена на следующем рисунке:
void
recursive_bisect(struct Vertex *graph, int n, int k) {
int k1, k2;
int n1, n2;
struct Vertex * subgraph1;
struct Vertex * subgraph2;
k1 = (k + 1) / 2;
k2 = k - k1;
n1 = n * k1 / k;
n2 = n - n1;
bisect(graph, n, subgraph1, n1, subgraph2, n2);
if (k1 > 1) recursive_bisect(subgraph1, n1, k1);
if (k2 > 1) recursive_bisect(subgraph2, n2, k2);
return;
}
В качестве входных параметров функция принимает массив вершин, содержащихся в текущем домене (graph), числа n -- количество вершин, k -- количество поддоменов, на который требуется разбить данный домен.
В теле функции вычисляется отношение между количеством поддоменов, на которые будут впоследствии разбиты полученные на текущей итерации поддомены (k1 и k2), и размеры поддоменов, которые будут получены на данной итерации (n1 и n2). С помощью вызова функции bisect осуществляется непосредственно разбиение на два поддомена. Затем функция recursive_bisect рекурсивно вызывается на полученных поддоменах до тех пор, пока остается необходимость в дальнейшем их разбиении.
Выбор конкретного алгоритма зависит от использованной функции bisect, которой осуществляется разбиение вершин на два подграфа на каждом из этапов. В случае координатной бисекции она имеет следующий вид:
void
coord_bisect(struct Vertex *graph, int n, struct Vertex *subgraph1, int n1, struct Vertex *subgraph2, int n2) {
int axis;
/* Calculate direction in which the initial graph is most elongated. */
axis = calculate_max_distance(graph, n);
/* Sort vertices along the selected axis. */
sort(graph, n, axis);
/* Create subgraphs. */
subgraph1 = create_subgraph(graph, 0, n1);
subgraph2 = create_subgraph(graph, n1, n);
return;
}
Входными параметрами функции являются массив вершин в домене, его размер, а также размеры полученных в результате разбиения поддоменов. Выходными параметрами являются массивы вершин, входящих в полученные поддомены. Следует отметить, что на вход достаточно передавать размер лишь одного из поддоменов, например, первого, поскольку размер второго явно из него следует, т.к. n1 + n2 == n. В данном примере оба размера передаются для наглядности и единообразия.
В процессе работы функции с помощью вызова функции calculate_max_distance выбирается координатная ось, вдоль которой сетка имеет наибольшую протяженность. Затем вершины сортируются вдоль этой оси, и создаются два поддомена: в первый входят вершины с индексами [0..n1) в отсортированном массиве, в второй -- [n1..n), где n1 равно \frac{n*\frac{(k+1)}{2}}{k}.
1.6 Последовательная сложность алгоритма
В течение каждого этапа выполняются следующие действия:
- Определение диаметра графа по каждой из координат -- m*O(n), где m -- размерность пространства, n -- количество вершин. Поскольку величина m, как правило, очень мала, ей можно пренебречь, оставив в качестве оценки сложности данного действия O(n).
- Поиск максимального расстояния -- осуществляется за O(m), также пренебрежимо мало.
- Сортировка. Наиболее эффективным алгоритмом последовательной сортировки является комбинация сортировки слиянием и пирамидальной сортировки [4]. Сложность как пирамидальной сортировки, так и сортировки слиянием оценивается как O(nlog_2(n)).
- Разбиение домена на поддомены осуществляется за O(1).
Исходя из этого, общая сложность каждой итерации оценивается сверху как O(nlog_2(n)), а их количество составляет \lceil log_2{k} \rceil. Таким образом, последовательная сложность метода -- O(log(k)*n*log(n)).
1.7 Информационный граф
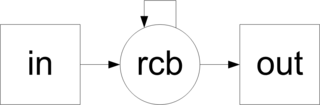
На рисунке 1 приведена общая схема работы метода. Входными данными является граф -- массив вершин, заданных в виде векторов координат. Выходными данными является множество массивов, элементами которых являются исходные вершины.
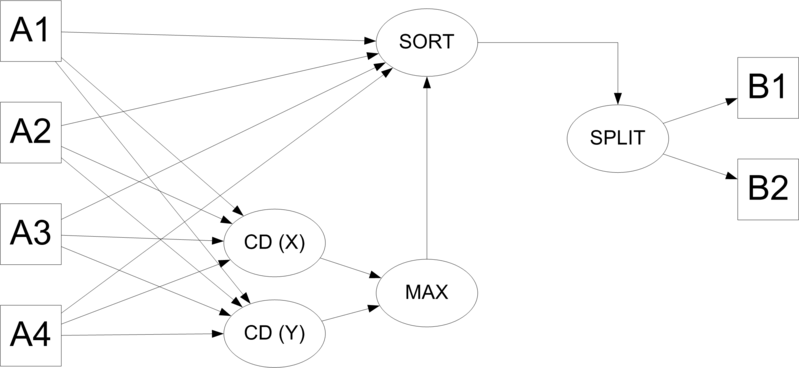
На рисунке 2 изображен информационный граф метода при распределении домена из 4 вершин, заданных в двумерном пространстве, на 2 поддомена. Входными данными являются вектора A1-A4, которые могут содержаться либо в исходном домене, либо в поддомене, полученном на предыдущей итерации. Выходные данные -- непересекающиеся множества векторов B1 и B2. В них содержатся вектора A1-A4. Вершины с меткой CD обозначают операцию вычисления диаметра домена (т.е. наибольшего расстояния между содержащимися в домене вершинами) по координатам x и y соответственно. Вершина MAX обозначает нахождение максимума, SORT -- сортировку, SPLIT -- разбиение домена на два поддомена равного размера.
1.8 Ресурс параллелизма алгоритма
При разбиении графа на k подграфов глубина рекурсии составляет \lceil log_2 k \rceil, а на каждом i шаге решается до 2^i подзадач. Поскольку подзадачи, возникающие на каждом шаге рекурсии, не имеют между собой информационных зависимостей, их решение можно распараллелить, получив таким образом некоторый прирост производительности. Исходя из того, что сложность этих подзадач примерно одинакова, можно считать, что их решение занимает на каждом ярусе примерно одинаковое время t. Пусть доступно бесконечное число одинаковых процессоров. Тогда на каждом ярусе размер входного массива равен \frac{n}{2^i}, где n -- исходное количество вершин, i -- номер яруса. При использовании сортировки сложностью O(n*log(n)) итоговую сложность можно вычислить как O(\sum\limits_{i=0}^{\lceil log_2 k \rceil}\frac{n}{2^i}*\log_2{\frac{n}{2^i}})= O(\sum\limits_{i=0}^{\lceil log_2 k \rceil}(n*\frac{(\log_2{n} - \log_2{2^i})}{2^i}))=
O(\sum\limits_{i=0}^{\lceil log_2 k \rceil}(n*\frac{(\log_2{n} - i)}{2^i}))= O(n*(\sum\limits_{i=0}^{\lceil log_2 k \rceil}(\frac{log_2{n}}{2^i})-\sum\limits_{i=0}^{\lceil log_2 k \rceil}(\frac{i}{2^i})))= O(n*(\log_2{n} - 1))=O(n*\log_2{n})-O(n)= O(n*\log_2{n}).
1.9 Входные и выходные данные алгоритма
Метод рекурсивной координатной бисекции работает над графами, часто -- сеточными. Входные данные удобно задавать в виде массива координат в n-мерном прострастве, т.е. векторов размерности n. Как правило, в прикладных задачах n составляет 2 или 3, т.е. заданы координаты на плоскости или в пространстве.
Входные данные алгоритма: Исходный граф G = (V, E), натуральное число k \in \N -- количество подграфов, на которое нужно осуществить разбиение.
Объем входных данных: n*m + |E|, где n -- количество векторов, m -- размерность пространства, E -- ребра в графе. Для равномерных сеток связи между вершинами можно не учитывать, т.е. объем входных данных можно ограничить n*m.
Выходные данные алгоритма: Множество G_1 .. G_k подграфов исходного графа G.
Объем выходных данных: n*m, где n -- количество векторов, m -- размерность пространства.
1.10 Свойства алгоритма
Метод рекурсивной координатной бисекции является устойчивым и детерминированным. Его вычислительная мощность пропорциональна log(k) (отношение последовательной сложности O(log(k)*n*log(n)) к параллельной O(n*log(n))).
Можно также отметить следующие особенности метода:
- Использование параллельного алгоритма рекурсивной координатной бисекции целесообразно при разбиении на большое число подграфов.
- Наибольшее ускорение достигается при разбиении на число подграфов, являющемся степенью двойки.
- Наибольшее ускорение достигается при использовании числа процессоров, являющегося степенью двойки.
- Небольшие накладные расходы, возникающие при обращении процессора к полной информации о разбиении.
- Отсутствие явного контроля над накладными расходами на передачу данных.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Масштабируемость алгоритма была исследована на примере реализации метода рекурсивной координатной бисекции, содержащейся в библиотеке ZOLTAN v3.83 [1] (файл example/C/simpleRCB.c). В части испытаний использованная программа была модифицирована таким образом, чтобы фиксировать количество поддоменов, на которое требуется разбить сетку. Для этого в функцию, непосредственно осуществляющую бисекцию Zoltan_LB_Partition(), был дополнительно передан параметр NUM_GLOBAL_PARTS (часть контекста struct Zoltan_Struct *zz).
В качестве тестового стенда было использовано ЭВМ BlueGene/P ВМК МГУ. Первый этап тестирования выполнялся в соответствии с методикой испытаний:
- фиксировано значение параметра k -- итоговое количество поддоменов (16);
- в качестве тестового набора входных данных была сгенерирована двумерная регулярная сетка размера N*N, где N -- 1024, 2048, 3072, 4096, 5120.
- для каждого размера сетки выполнена серия запусков на различном количестве процессоров: 1, 2, 4, [8..128] c шагом 8 (8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 128).
Тестовая программа и сама библиотека ZOLTAN были скомпилированы с помощью mpicc 1.1 (gcc 4.1.2), параметры компиляции стандартные, приведены в Makefile/make everything. Для запуска использовался скрипт, одновременно ставящий в очередь все задачи с одинаковым размером входной сетки. Пример запуска одной задачи: mpisubmit.bg -n $3 --stdout result_$2_$1_$3.txt -w 00:15:00 simpleRCB.exe -- mesh$1.txt $2 $1; $1 -- размер сетки, $2 -- количество поддоменов, $3 -- количество процессоров.
Полученные результаты замеров времени работы показаны на рис. 3 и 4. На рис. 4 для наглядности использована логарифмическая шкала для количества процессоров, а также исключены результаты для запусков при количестве процессоров, не являющемся степенью 2. Соответствующие им результаты эффективности распараллеливания приведены на рис. 5 и 6.
По мере увеличения количества процессоров масштабируемость по данным стремится к линейной.
Минимальное значение эффективности распараллеливания составило 0.017 (сетка 1024*1024, 128 процессоров), максимальное -- 0.717 (сетка 4096*4096, 2 процессора).
На рис. 3 было обнаружено небольшое увеличение производительности алгоритма при количестве процессоров, равном количеству поддоменов, на которое требовалось разбить сетку (16). Это обусловлено тем, что в случае совпадения количества поддоменов и процессоров, количество вершин, приходящихся на каждый из процессоров в течение обработки, оптимально. В связи с этим было проведено дополнительное исследование производительности алгоритма в таком режиме, т.е. при всех запусках итоговое количество поддоменов совпадало с количеством используемых процессоров. Такое использование характерно для решения задачи балансировки нагрузки, а также предварительного разбиения вершин сетки по процессорам, для чего обычно и используется рекурсивная координатная бисекция. Результат тестирования приведен на рис. 7.
На графике наблюдается существенное увеличение производительности при числе процессоров, равном 2, что обусловлено наименьшими затратами на передачу данных. Дальнейшее увеличение числа процессоров (и, одновременно, поддоменов) приводит к одинаковому результату, худшему, чем в случае двух процессоров.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Наиболее широко в настоящее время применяется параллельный алгоритм рекурсивной координатной бисекции, реализованный в пакете ZOLTAN (Zoltan2) [2]. Он может разбивать поддомены двумя способами:
- BISECTION -- выбирается кандидат из отрезка [L, R], чье значение ближе всего к (L+R)/2.
- RANDOM -- выбирается первый кандидат -- медиана коллекции локальных медиан каждого процесса. Затем осуществляется бинарный поиск по оставшимся локальным медианам. Если медиана все еще не найдена, каждуй процесс предоставляет кандидата, выбранного случайным образом из значений в интересующей области, и бинарный поиск производится среди них. Последний шаг повторяется на сужаемой описанным выше образом области до тех пор, пока медиана не будет найдена.
Для осуществления разрезов области не пересортируются, а используют древовидную структуру, хранящую информацию о ранее произведенных разрезах. Весь массив исходных данных хранится распределенным по нескольким процессорам.
Метод рекурсивной координатной бисекции сеток реализован в пакете GridSpiderPar [3]. Использованный в нем алгоритм отличается от аналогичного алгоритма в пакете ZOLTAN тем, что в нем секущая плоскость (медиана) при необходимости разрезается по нескольким координатам. Это позволяет обрабатывать ситуации наличия на одной плоскости множества узлов с одинаковым значением координаты, что характерно для регулярных сеток. В пакете ZOLTAN вершины из медианы распределяются по областям произвольным образом, что увеличивает число разрезанных ребер.
Помимо приведенных выше инструментов, метод рекурсивной координатной бисекции (как последовательный, так и параллельный) часто реализуется в научных и практических работах авторами самостоятельно, что обусловлено его простотой и достаточно высокой эффективностью, а также возможностью легко адаптировать к требованиям, возникающим при решении конкретной задачи.
3 Литература
- ↑ M. Berger and S. Bokhari. "A partitioning strategy for nonuniform problems on multiprocessors." IEEE Trans. Computers, C-36 (1987) 570-580.
- ↑ Якобовский М.В. Параллельные алгоритмы сортировки больших объемов данных // Фундаментальные физико-математические проблемы и моделирование технико-технологических систем: Сб. науч. тр. : Янус-К, 2004, c. 235-249.
- ↑ Головченко, Е. Н., Якобовский, М. В. (2015). Пакет параллельной декомпозиции больших сеток GridSpiderPar. вычислительные методы и программирование, 16, 507.
- ↑ Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2