Алгоритм Флойда-Уоршелла: различия между версиями
| [непроверенная версия] | [досмотренная версия] |
Daryin (обсуждение | вклад) (Общее описание алгоритма) |
ASA (обсуждение | вклад) |
||
| (не показано 28 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == Свойства и структура | + | {{level-a}} |
| + | |||
| + | Автор: Екатерина Шевченко | ||
| + | == Свойства и структура алгоритма == | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Алгоритм Флойда-Уоршелла<ref>Roy, Bernard. “Transitivité Et Connexité.” Comptes Rendus De l'Académie Des Sciences 249 (1959): 216–218.</ref><ref>Warshall, Stephen. “A Theorem on Boolean Matrices.” Journal of the ACM 9, no. 1 (January 1, 1962): 11–12. doi:10.1145/321105.321107.</ref><ref>Floyd, Robert W. “Algorithm 97: Shortest Path.” Communications of the ACM 5, no. 6 (June 1, 1962): 345. doi:10.1145/367766.368168.</ref> предназначен для решения [[Поиск кратчайшего пути для всех пар вершин (APSP)|задачи поиска всех кратчайших путей на графе]]. Для заданного ориентированного взвешенного графа алгоритм находит кратчайшие расстояния между всеми парами вершин. | + | '''Алгоритм Флойда-Уоршелла'''<ref>Roy, Bernard. “Transitivité Et Connexité.” Comptes Rendus De l'Académie Des Sciences 249 (1959): 216–218.</ref><ref>Warshall, Stephen. “A Theorem on Boolean Matrices.” Journal of the ACM 9, no. 1 (January 1, 1962): 11–12. doi:10.1145/321105.321107.</ref><ref>Floyd, Robert W. “Algorithm 97: Shortest Path.” Communications of the ACM 5, no. 6 (June 1, 1962): 345. doi:10.1145/367766.368168.</ref> предназначен для решения [[Поиск кратчайшего пути для всех пар вершин (APSP)|задачи поиска всех кратчайших путей на графе]]. Для заданного ориентированного взвешенного графа алгоритм находит кратчайшие расстояния между всеми парами вершин за время <math>O(n^3)</math>. Алгоритм применим к графам с произвольными, в том числе с отрицательными, весами. Таким образом, он является более общим в сравнении с [[Алгоритм Дейкстры|алгоритмом Дейкстры]], который не работает с отрицательными весами ребер. Также алгоритм распознаёт наличие отрицательных циклов. |
| + | |||
| + | === Математическое описание алгоритма === | ||
| + | |||
| + | Имеем граф <math>G=(V,E)</math>, в котором каждая вершина пронумерована от <math>1</math> до <math>|V|</math>. Сформируем матрицу смежности <math>D</math>. Эта матрица имеет размер <math>|V|*|V|</math> и каждому ее элементу <math>D_{ij}</math> присвоен вес ребра, соединяющего вершину <math>i</math> с вершиной <math>j</math>. Заметим, что в силу ориентированности графа <math>G</math> матрица <math>D</math> может быть несимметрична. | ||
| + | |||
| + | По мере выполнения алгоритма данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины <math>i</math> в вершину <math>j</math>. | ||
| − | = | + | Полагаем диагональные элементы <math>D_{ii}</math> равными нулю, а недиагональные элементы, соответствующие не инцидентным вершинам (не имеющим общего ребра), положим равными бесконечности или числу, заведомо большему возможного расстояния между ребрами. |
| + | |||
| + | Ключевая часть алгоритма состоит из трех циклов:<br> | ||
| + | Для k от 1 до |V| выполнять <br> | ||
| + | Для i от 1 до |V| выполнять <br> | ||
| + | Для j от 1 до |V| выполнять <br> | ||
| + | Если <math>{D_{ik}+D_{kj} < D_{ij}}</math>, то <math>{D_{ij} := D_{ik}+D_{kj}}</math>. <br> | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| + | |||
| + | Основной операцией алгоритма является релаксация элементов матрицы смежности: если <math>{D_{ik}+D_{kj} < D_{ij}}</math>, то производится присваивание <math>{D_{ij} := D_{ik}+D_{kj}}</math>. <br> | ||
| + | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | === | + | Ключевая часть алгоритма состоит из трех циклов:<br> |
| + | Для k от 1 до |V| выполнять <br> | ||
| + | Для i от 1 до |V| выполнять <br> | ||
| + | Для j от 1 до |V| выполнять <br> | ||
| + | Если <math>{D_{ik}+D_{kj} < D_{ij}}</math>, то <math>{D_{ij} := D_{ik}+D_{kj}}</math>. <br> | ||
| + | |||
| + | При этом вычисляются минимумы из двух чисел <math>min({D_{ik}+D_{kj}}, D_{ij})</math> и их значения становятся новыми значениями элементов смежной матрицы. <br> | ||
| + | === Схема реализации последовательного алгоритма === | ||
| + | matrix - матрица смежности, numberOfVert - число вершин в графе | ||
| + | |||
| + | //Пробегаемся по всем вершинам и ищем более короткий путь | ||
| + | //через вершину k | ||
| + | for(int k = 0; k < numberOfVert; k++) { | ||
| + | for(int i = 0; i < numberOfVert; i++) { | ||
| + | for(int j = 0; j < numberOfVert; j++) { | ||
| + | //Новое значение ребра равно минимальному между старым | ||
| + | //и суммой ребер i <-> k + k <-> j (если через k пройти быстрее) | ||
| + | matrix[i][j] = min(matrix[i][j], matrix[i][k] + matrix[k][j]); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | Время выполнения этой программы, очевидно, имеет порядок <math>O(n^3)</math>, поскольку в ней практически нет ничего, кроме вложенных друг в друга трех циклов. | ||
| + | |||
=== Информационный граф === | === Информационный граф === | ||
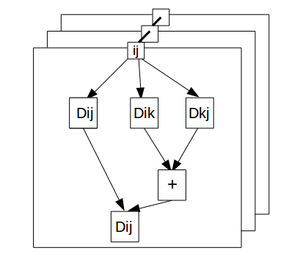
| − | === | + | [[file:Graphforfloyd.png|thumb|center|300px|Рис.1. Информационная структура предельной параллелизации алгоритма Флойда-Уоршелла]] |
| − | === | + | |
| − | === Свойства алгоритма=== | + | На приведенном далее информационном графе нижний уровень параллелизма обозначен в горизонтальных плоскостях. Множество всех плоскостей представляет собой верхний уровень параллелизма (операции в каждой плоскости могут выполняться параллельно). Верхний уровень параллелизма заключается в параллельном подсчете дистанций для различных элементов матрицы смежности, и на рисунке отмечен разными плоскостями. |
| − | == Программная реализация | + | |
| + | === Ресурс параллелизма алгоритма === | ||
| + | В последовательном алгоритме единственная операция - это нахождение минимума, ее нет смысла распараллеливать. Вся сложность алгоритма заключается в полном переборе «матрицы смежности». Идея параллельных схем алгоритма Флойда-Уоршелла состоит в том, чтобы модифицировать матрицу смежности одновременно несколькими процессорами. Можно выделить два основных подхода. | ||
| + | |||
| + | Первый подход. В распоряжении имеется такое количество процессоров, что можно отдать каждому ровно по одному элементу <math>D_{ij}</math>, чтобы он считал для этого элемента минимум. | ||
| + | |||
| + | Второй подход. В распоряжении ограниченное количество процессов. В этом случае грамотным решением будет отдать каждому процессору(или процессу) по одной строке матрицы смежности. Пусть каждый процесс посчитает минимумы в своей строке матрицы и отдаст результаты корневому процессу, это прилично ускорит работу алгоритма. | ||
| + | |||
| + | Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы <math>D</math>. Всего в подзадачах <math>{n^2/p}</math> таких элементов, число итераций алгоритма равно <math>n</math>, таким образом, показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид (<math>p</math> – число процессоров): <math>{Sp = n^3/(n^3/p) = p}</math>, <math>{Ep = n^3/(p(n^3⁄p)) = 1}</math>. | ||
| + | |||
| + | === Входные и выходные данные алгоритма === | ||
| + | Входные данные: Матрица смежности D. Перед работой алгоритма матрица D заполняется длинами рёбер графа (или запредельно большим числом M, если ребра нет). <br> | ||
| + | Выходные данные: Матрица кратчайших расстояний D. | ||
| + | |||
| + | === Свойства алгоритма === | ||
| + | |||
| + | Алгоритм может распознавать наличие отрицательных циклов: такой цикл существует, если один из диагональных элементов матрицы расстояний становится меньше нуля. | ||
| + | |||
| + | == Программная реализация алгоритма == | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | + | === Возможные способы и особенности параллельной реализации алгоритма === | |
| − | === Возможные способы и особенности реализации | + | === Результаты прогонов === |
| − | === | ||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | + | ||
== Литература == | == Литература == | ||
<references /> | <references /> | ||
| + | |||
| + | [[Категория:Начатые статьи]] | ||
| + | |||
| + | [[en:Floyd-Warshall algorithm]] | ||
Текущая версия на 10:54, 5 июля 2022
Автор: Екатерина Шевченко
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Флойда-Уоршелла[1][2][3] предназначен для решения задачи поиска всех кратчайших путей на графе. Для заданного ориентированного взвешенного графа алгоритм находит кратчайшие расстояния между всеми парами вершин за время [math]O(n^3)[/math]. Алгоритм применим к графам с произвольными, в том числе с отрицательными, весами. Таким образом, он является более общим в сравнении с алгоритмом Дейкстры, который не работает с отрицательными весами ребер. Также алгоритм распознаёт наличие отрицательных циклов.
1.2 Математическое описание алгоритма
Имеем граф [math]G=(V,E)[/math], в котором каждая вершина пронумерована от [math]1[/math] до [math]|V|[/math]. Сформируем матрицу смежности [math]D[/math]. Эта матрица имеет размер [math]|V|*|V|[/math] и каждому ее элементу [math]D_{ij}[/math] присвоен вес ребра, соединяющего вершину [math]i[/math] с вершиной [math]j[/math]. Заметим, что в силу ориентированности графа [math]G[/math] матрица [math]D[/math] может быть несимметрична.
По мере выполнения алгоритма данная матрица будет перезаписываться: в каждую из ее ячеек внесется значение, определяющее оптимальную длину пути из вершины [math]i[/math] в вершину [math]j[/math].
Полагаем диагональные элементы [math]D_{ii}[/math] равными нулю, а недиагональные элементы, соответствующие не инцидентным вершинам (не имеющим общего ребра), положим равными бесконечности или числу, заведомо большему возможного расстояния между ребрами.
Ключевая часть алгоритма состоит из трех циклов:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если [math]{D_{ik}+D_{kj} \lt D_{ij}}[/math], то [math]{D_{ij} := D_{ik}+D_{kj}}[/math].
1.3 Вычислительное ядро алгоритма
Основной операцией алгоритма является релаксация элементов матрицы смежности: если [math]{D_{ik}+D_{kj} \lt D_{ij}}[/math], то производится присваивание [math]{D_{ij} := D_{ik}+D_{kj}}[/math].
1.4 Макроструктура алгоритма
Ключевая часть алгоритма состоит из трех циклов:
Для k от 1 до |V| выполнять
Для i от 1 до |V| выполнять
Для j от 1 до |V| выполнять
Если [math]{D_{ik}+D_{kj} \lt D_{ij}}[/math], то [math]{D_{ij} := D_{ik}+D_{kj}}[/math].
При этом вычисляются минимумы из двух чисел [math]min({D_{ik}+D_{kj}}, D_{ij})[/math] и их значения становятся новыми значениями элементов смежной матрицы.
1.5 Схема реализации последовательного алгоритма
matrix - матрица смежности, numberOfVert - число вершин в графе
//Пробегаемся по всем вершинам и ищем более короткий путь
//через вершину k
for(int k = 0; k < numberOfVert; k++) {
for(int i = 0; i < numberOfVert; i++) {
for(int j = 0; j < numberOfVert; j++) {
//Новое значение ребра равно минимальному между старым
//и суммой ребер i <-> k + k <-> j (если через k пройти быстрее)
matrix[i][j] = min(matrix[i][j], matrix[i][k] + matrix[k][j]);
}
}
}
1.6 Последовательная сложность алгоритма
Время выполнения этой программы, очевидно, имеет порядок [math]O(n^3)[/math], поскольку в ней практически нет ничего, кроме вложенных друг в друга трех циклов.
1.7 Информационный граф
На приведенном далее информационном графе нижний уровень параллелизма обозначен в горизонтальных плоскостях. Множество всех плоскостей представляет собой верхний уровень параллелизма (операции в каждой плоскости могут выполняться параллельно). Верхний уровень параллелизма заключается в параллельном подсчете дистанций для различных элементов матрицы смежности, и на рисунке отмечен разными плоскостями.
1.8 Ресурс параллелизма алгоритма
В последовательном алгоритме единственная операция - это нахождение минимума, ее нет смысла распараллеливать. Вся сложность алгоритма заключается в полном переборе «матрицы смежности». Идея параллельных схем алгоритма Флойда-Уоршелла состоит в том, чтобы модифицировать матрицу смежности одновременно несколькими процессорами. Можно выделить два основных подхода.
Первый подход. В распоряжении имеется такое количество процессоров, что можно отдать каждому ровно по одному элементу [math]D_{ij}[/math], чтобы он считал для этого элемента минимум.
Второй подход. В распоряжении ограниченное количество процессов. В этом случае грамотным решением будет отдать каждому процессору(или процессу) по одной строке матрицы смежности. Пусть каждый процесс посчитает минимумы в своей строке матрицы и отдаст результаты корневому процессу, это прилично ускорит работу алгоритма.
Для параллельного алгоритма на отдельной итерации каждый процессор выполняет обновление элементов матрицы [math]D[/math]. Всего в подзадачах [math]{n^2/p}[/math] таких элементов, число итераций алгоритма равно [math]n[/math], таким образом, показатели ускорения и эффективности параллельного алгоритма Флойда имеют вид ([math]p[/math] – число процессоров): [math]{Sp = n^3/(n^3/p) = p}[/math], [math]{Ep = n^3/(p(n^3⁄p)) = 1}[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: Матрица смежности D. Перед работой алгоритма матрица D заполняется длинами рёбер графа (или запредельно большим числом M, если ребра нет).
Выходные данные: Матрица кратчайших расстояний D.
1.10 Свойства алгоритма
Алгоритм может распознавать наличие отрицательных циклов: такой цикл существует, если один из диагональных элементов матрицы расстояний становится меньше нуля.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Возможные способы и особенности параллельной реализации алгоритма
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
3 Литература
- ↑ Roy, Bernard. “Transitivité Et Connexité.” Comptes Rendus De l'Académie Des Sciences 249 (1959): 216–218.
- ↑ Warshall, Stephen. “A Theorem on Boolean Matrices.” Journal of the ACM 9, no. 1 (January 1, 1962): 11–12. doi:10.1145/321105.321107.
- ↑ Floyd, Robert W. “Algorithm 97: Shortest Path.” Communications of the ACM 5, no. 6 (June 1, 1962): 345. doi:10.1145/367766.368168.