Участник:Лукьянова Анна/Алгоритм кластеризации с использованием представлений2: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
(не показано 11 промежуточных версий 3 участников)
Строка 1: Строка 1:
−
{{Assignment|IgorS}}
 
−
 
 
Основные авторы описания: [[U:Лукьянова Анна|А.Я. Лукьянова]]
 
Основные авторы описания: [[U:Лукьянова Анна|А.Я. Лукьянова]]
  
Строка 62: Строка 60:
 
Алгоритм '''CURE (Clustering Using REpresentatives)''' выполняет иерархическую кластеризацию с использованием набора определяющих точек для определения объекта в кластер. Относится к алгомеративным методам.
 
Алгоритм '''CURE (Clustering Using REpresentatives)''' выполняет иерархическую кластеризацию с использованием набора определяющих точек для определения объекта в кластер. Относится к алгомеративным методам.
  
−
Эта группа методов характеризуется последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров.
+
''Назначение'': кластеризация очень больших наборов числовых данных.
−
 
 
−
Назначение: кластеризация очень больших наборов числовых данных.
 
−
 
 
−
Ограничения: эффективен для данных низкой размерности, работает только на числовых данных.  
 
  
−
Достоинства:  
+
''Достоинства'':  
 
*выполняет кластеризацию на высоком уровне даже при наличии выбросов;
 
*выполняет кластеризацию на высоком уровне даже при наличии выбросов;
 
*выделяет кластеры сложной формы и различных размеров,  
 
*выделяет кластеры сложной формы и различных размеров,  
 
*обладает линейно зависимыми требованиями к месту хранения данных и временную сложность для данных высокой размерности.
 
*обладает линейно зависимыми требованиями к месту хранения данных и временную сложность для данных высокой размерности.
  
−
Недостатки: есть необходимость в задании пороговых значений и количества кластеров.  
+
''Недостатки'': есть необходимость в задании пороговых значений и количества кластеров.  
  
 
Описание алгоритма :
 
Описание алгоритма :
Строка 85: Строка 79:
 
'''Шаг 2:''' Формирование «кучи» в оперативной памяти, расчет расстояния до ближайшего кластера (строки данных) для каждого кластера. При формировании кучи кластеры сортируются по возрастанию дистанции от кластера до ближайшего кластера. Расстояние между кластерами определяется по двум ближайшим элементам из соседних кластеров. Для определения расстояния между кластерами используются «манхеттенская», «евклидова» метрики или похожие на них функции.
 
'''Шаг 2:''' Формирование «кучи» в оперативной памяти, расчет расстояния до ближайшего кластера (строки данных) для каждого кластера. При формировании кучи кластеры сортируются по возрастанию дистанции от кластера до ближайшего кластера. Расстояние между кластерами определяется по двум ближайшим элементам из соседних кластеров. Для определения расстояния между кластерами используются «манхеттенская», «евклидова» метрики или похожие на них функции.
  
−
''Метрика Евклида:'' <math>\rho(p,k) = \sqrt{\sum_{i=1}^n (p_{i} - k_{i})^2}</math>
+
'''Шаг 3:''' Слияние ближних кластеров в один кластер. Новый кластер получает все точки входящих в него входных данных. Расчет расстояния до остальных кластеров для новообразованного кластера. Для расчета расстояния кластеры делятся на две группы: первая группа – кластеры, у которых ближайшими кластерами считаются кластеры, входящие в новообразованный кластер, остальные кластеры – вторая группа. И при этом для кластеров из первой группы, если расстояние до новообразованного кластера меньше чем до предыдущего ближайшего кластера, то ближайший кластер меняется на новообразованный кластер. В противном случае ищется новый ближайший кластер, но при этом не берутся кластеры, расстояния до которых больше, чем до новообразованного кластера. Для кластеров второй группы выполняется следующее: если расстояние до новообразованного  кластера ближе, чем предыдущий ближайший кластер, то ближайший кластер меняется. В противном случае ничего не происходит.
  
−
''«Манхеттенская» метрика:'' <math>\rho(p,k) =\sum_{i=1}^n |p_{i} - k_{i}|</math>
+
'''Шаг 4:''' Переход на шаг 3, если не получено требуемое количество кластеров.
  
 +
== Математическое описание алгоритма ==
  
 +
Прежде всего, алгоритм использует случайное разбиение выборки из <math> s </math> элементов на <math> p </math> частей, которые могут поместиться в память отдельной машины кластера. Затем во время первого прохода алгоритм уменьшает число кластеров в каждой подвыборке до <math> \frac{s}{pq} </math>, где <math> q \geq 1 </math> – некоторая константа (происходит объединение ближайших кластеров). Для определения расстояния между кластерами используются «манхеттенская», «евклидова» метрики или похожие на них функции.
  
−
'''Шаг 3:''' Слияние ближних кластеров в один кластер. Новый кластер получает все точки входящих в него входных данных. Расчет расстояния до остальных кластеров для новообразованного кластера. Для расчета расстояния кластеры делятся на две группы: первая группа – кластеры, у которых ближайшими кластерами считаются кластеры, входящие в новообразованный кластер, остальные кластеры – вторая группа. И при этом для кластеров из первой группы, если расстояние до новообразованного кластера меньше чем до предыдущего ближайшего кластера, то ближайший кластер меняется на новообразованный кластер. В противном случае ищется новый ближайший кластер, но при этом не берутся кластеры, расстояния до которых больше, чем до новообразованного кластера. Для кластеров второй группы выполняется следующее: если расстояние до новообразованного  кластера ближе, чем предыдущий ближайший кластер, то ближайший кластер меняется. В противном случае ничего не происходит.
+
''Метрика Евклида:'' <math>\rho(p,k) = \sqrt{\sum_{i=1}^n (p_{i} - k_{i})^2}</math>
  
−
'''Шаг 4:''' Переход на шаг 3, если не получено требуемое количество кластеров.
+
''«Манхеттенская» метрика:'' <math>\rho(p,k) =\sum_{i=1}^n |p_{i} - k_{i}|</math>
  
−
Выбранные точки сдвигаются на следующем шаге на <math>\alpha</math> к центроиду кластера. Алгоритм становится основанным на методе поиска центроида при <math>\alpha = 1</math>, и основанным на всех точках кластера при <math>\alpha = 0</math>.
+
Если расстояние между ближайшей парой кластеров больше некоторого парогового(критического) значения, то объединения не происходит.
 +
 +
Для последующего шага на вход кластеризации подаются только представительные точки <math>c</math> кластеров, полученных на предыдущем этапе. В ходе второго прохода алгоритма кластеризации остаются представительные точки для заданного количества кластеров. Алгоритм использует представительные точки, как метки, задающие форму и размер кластера.
  
−
[[Файл:Factor_a.png|400px|thumb|center| Рисунок 2: Чувствительность алгоритма к параметру <math>\alpha </math>.]]
+
Число точек представителей выбирается в зависимости от данных. Если возможно появление кластеров сложной формы, то точек должно быть больше, чтобы выявить их форму. В оригинальной статье авторы показывают что уже при <math>c</math> равном <math>10</math> достигается неплохая эффективность.
  
−
== Математическое описание алгоритма ==
+
[[Файл:Param_c.png|400px|thumb|center| Рисунок 2: Результат работы алгоритка в зависимости от количесва представлений <math>c</math>.]]
  
−
Прежде всего, алгоритм использует случайное разбиение выборки из <math> n </math> элементов на <math> p </math> частей, которые могут поместиться в память отдельной машины кластера. Затем во время первого прохода алгоритм уменьшает число кластеров в каждой подвыборке до <math> \frac{n}{pq} </math>, где <math> q \geq 1 </math> – некоторая константа. Для последующего шага на вход кластеризации подаются только представительные точки <math>c</math> кластеров, полученных на предыдущем этапе. В ходе второго прохода алгоритма кластеризации остаются представительные точки для заданного количества кластеров. Алгоритм использует представительные точки, как метки, задающие форму и размер кластера.
+
Из рисунка видно, что при меньших значениях <math>c</math> качество работы алгоритма ухудшается
  
 +
Выбранные точки сдвигаются на <math>\alpha</math> к центроиду кластера. Алгоритм становится основанным на методе поиска центроида при <math>\alpha = 1</math>, и основанным на всех точках кластера при <math>\alpha = 0</math>.
  
 +
[[Файл:Factor_a.png|400px|thumb|center| Рисунок 3: Чувствительность алгоритма к параметру <math>\alpha </math>.]]
  
 
== Вычислительное ядро алгоритма ==
 
== Вычислительное ядро алгоритма ==
Строка 116: Строка 116:
 
== Схема реализации последовательного алгоритма ==
 
== Схема реализации последовательного алгоритма ==
  
−
Псевдокод
+
Входные параметры: набор входных данных <math>S</math>, содержащий <math>m</math> точек в <math>n</math>-мерном пространстве
−
 
+
и требуемое количество кластеров <math>k</math>. Начиная с отдельных точек в виде отдельных кластеров, на каждом шаге ближайшая пара кластеров объединяются, чтобы сформировать новый кластер.Процесс повторяется до тех пор, пока не достигнет <math>k</math>.
−
Input : A set of points S
 
−
 
 
−
Output : ''k'' clusters
 
−
 
 
−
*  For every cluster u (each input point), in u.mean and u.rep store the mean of the points in the cluster and a set of ''c'' representative points of the cluster (initially ''c'' = 1 since each cluster has one data point). Also u.closest stores the cluster closest to u.
 
−
*  All the input points are inserted into a k-d tree T
 
−
*  Treat each input point as separate cluster, compute u.closest for each u and then insert each cluster into the heap Q. (clusters are arranged in increasing order of distances between u and u.closest).
 
−
*  While size(Q) &gt; ''k''
 
−
*      Remove the top element of Q(say u) and merge it with its closest cluster u.closest(say v) and compute the new representative points for the merged cluster w.
 
−
*      Remove u and v from T and Q.
 
−
*      For all the clusters x in Q, update x.closest and relocate x
 
−
*          insert w into Q
 
−
*      repeat
 
−
 
 
−
 
 
  
 +
'''procedure''' cluster(S,k)
 +
'''begin'''
 +
1. T:=build_kd_tree(S)
 +
2. Q:-build_heap(S)
 +
3. '''while''' size(Q)>k '''do''' {
 +
4.    u:=extract_min(Q)
 +
5.    v:= u.closest
 +
6.    delete(Q, V)
 +
7.    w := merge(u,v)
 +
8.    delete_rep(T, u); delete_rep(T, v); insert_rep(T, w)
 +
9.    w.closest := x /* x is an arbitrary cluster in Q */
 +
10.    '''for each''' x \in Q'''do''' {
 +
11.      '''if''' dist(w, x) < dist(w, w.closest)
 +
12.              w.closest := x
 +
13.      '''if''' x.closest is either u or w { 
 +
14.            ''' if''' dist(x, x.closest) < dist(x, w)
 +
15.                x.closest := closest_cluster(T, x, dist(x, w))
 +
16.            '''else'''
 +
17.              x.closest := w
 +
18.            relocate(Q, x)
 +
19.        }
 +
20.      '''else if''' dist(x, x.closest) > d&(x, w) {
 +
21.            x.closest := w
 +
22.            relocate(Q, x)
 +
23.        }
 +
24.      }
 +
25.      insert(Q, w)
 +
26. }
 +
'''end'''
  
 
== Последовательная сложность алгоритма ==
 
== Последовательная сложность алгоритма ==
Строка 144: Строка 158:
 
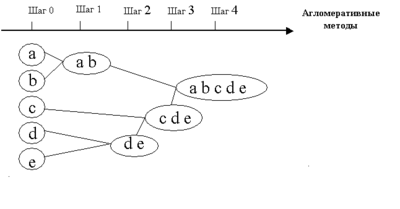
В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер.
 
В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер.
  
−
[[Файл:Metod.png|400px|thumb|center| Рисунок 3: Дендрограмма агломеративных методов]]
+
[[Файл:Metod.png|400px|thumb|center| Рисунок 4: Дендрограмма агломеративных методов]]
  
 
== Ресурс параллелизма алгоритма ==
 
== Ресурс параллелизма алгоритма ==
Строка 152: Строка 166:
 
== Входные и выходные данные алгоритма ==
 
== Входные и выходные данные алгоритма ==
  
−
'''Входные данные:''' набор данных <math> S </math> , количество кластеров <math>k</math>, число точек представителей <math>c</math>, параметр <math>\alpha</math>, параметр <math>\gamma</math>, <math>m</math> число точек для кластеризации, <math>n</math> размерность.
+
'''Входные данные:''' набор данных <math> S </math> , количество кластеров <math>k</math>, число точек представителей <math>c</math>, параметр <math>\alpha</math>, параметр <math>q</math>, <math>p</math> число разбиений выборки, <math>n</math> размерность.
 +
 
 +
Параметр <math>\alpha</math> для сжатия точек представления к центру кластера.
 +
 
 +
'''Выходные данные:''' требуемое количество <math> k </math> крастеров
 +
 
 +
===Оптимальный выбор параметров для алгоритма===
  
−
Параметр <math>\alpha</math> для сжатия точек представления к центру кластера. В оригинальной статье авторы показывают что <math>\alpha</math> от <math>0.2</math> до <math>0.7</math> помогает хорошо выявлять несферические кластеры и подавлять редкие выбросы.
+
*размер случайной выборки <math> S </math> (''а'')
  
−
[[Файл:Factor_a.png|400px|thumb|center| Рисунок 2: Чувствительность алгоритма к параметру <math>\alpha </math>.]]
+
При запуске CURE со случайными размерами выборки в пределах от 500 до 5000 видно, что при размерах до 2000 были найдены кластеры низкого качества, начиная с 2500 точек и выше (2,5% от установленного размера данных), CURE всегда правильно определяет кластеры.
  
−
Параметр <math>\gamma</math> задаёт какая часть от <math>m</math> точек будет использована при случайной выборке точек на шаге 2.
+
*число точек представителей  <math> c </math> (''b'')
 +
В оригинальной статье авторы показывают что уже при <math> c </math> равном <math>10</math> достигается неплохая эффективность.
  
−
Число точек представителей выбирается в зависимости от данных. Если возможно появление кластеров сложной формы, то точек должно быть больше, чтобы выявить их форму. В оригинальной статье авторы показывают что уже при <math>c</math> равном <math>10</math> достигается неплохая эффективность.
+
*число разбиений выборки <math> p </math> ('''c''')
 +
<math> p </math> должно быть выбрано таким, что <math> \frac{s}{pq} </math> > <math> k </math>
  
−
[[Файл:Param_c.png|400px|thumb|center| Рисунок 4: Результат работы алгоритка в зависимости от количесва представлений <math>c</math>.]]
+
*размерность (''d'')
 +
CURE хорошо себя чувствует при больших размерностях
  
−
Из рисунка видно, что при меньших значениях <math>c</math> качество работы алгоритма ухудшается
+
*сжимающий фактор <math>\alpha</math>
 +
В оригинальной статье авторы показывают что <math>\alpha</math> от 0.2 до 0.7 помогает хорошо выявлять несферические кластеры и подавлять редкие выбросы.
  
−
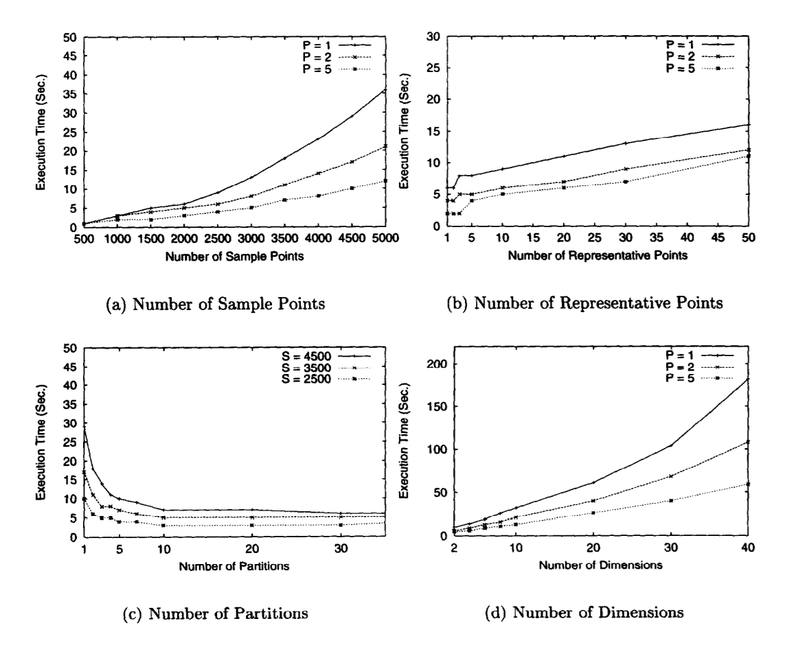
'''Выходные данные:''' требуемое количество <math> k </math> крастеров
+
[[Файл:4pic.png|800px|thumb|center| Рисунок 5: Влияние параметров <math> S </math>, <math> c </math>, <math> p </math> и размерности на работу алгоритма.]]
  
 
== Свойства алгоритма ==  
 
== Свойства алгоритма ==  
Строка 186: Строка 210:
  
 
== Масштабируемость алгоритма и его реализации ==
 
== Масштабируемость алгоритма и его реализации ==
 +
 +
будет..
  
 
==Динамические характеристики и эффективность реализации алгоритма==
 
==Динамические характеристики и эффективность реализации алгоритма==

Текущая версия на 17:27, 29 ноября 2016

Основные авторы описания: А.Я. Лукьянова

Содержание

1 ЧАСТЬ. Свойства и структура алгоритмa

1.1 Общее описание алгоритма

1.1.1 Понятие кластеризации

Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.

Применение кластерного анализа в общем виде сводится к следующим этапам:

  1. Отбор выборки объектов для кластеризации.
  2. Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных.
  3. Вычисление значений меры сходства между объектами.
  4. Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
  5. Представление результатов анализа.


Классификация алгоритмов


Методы по способу обработки данных:

Иерархические методы: строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.о. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.

  • Агломеративные методы AGNES (Agglomerative Nesting) - характеризуются последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров. В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор,

пока все объекты не будут составлять один кластер.

  • Дивизимные методы DIANA (Divisive Analysis) - характеризуются последовательным разделением исходного кластера, состоящего из всех объектов, и соответствующим увеличением числа кластеров. В начале работы алгоритма все объекты принадлежат одному кластеру, который на последующих шагах делится на меньшие кластеры, в результате образуется последовательность расщепляющих групп.

Неиерархические методы: строят одно разбиение объектов на кластеры.

  • Итеративные

Алгоритмы по способу анализа данных:

  • Четкие (непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру;
  • Нечеткие (пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.

Методы по количеству применений алгоритмов кластеризации:

  • С одноэтапной кластеризацией;
  • С многоэтапной кластеризацией.

Методы по возможности расширения объема обрабатываемых данных:

  • Масштабируемые;
  • Немасштабируемые

Методы по времени выполнения кластеризации:

  • Потоковые (on-line);
  • Не потоковые (off-line).

1.1.2 CURE

Алгоритм CURE (Clustering Using REpresentatives) выполняет иерархическую кластеризацию с использованием набора определяющих точек для определения объекта в кластер. Относится к алгомеративным методам.

Назначение: кластеризация очень больших наборов числовых данных.

Достоинства:

  • выполняет кластеризацию на высоком уровне даже при наличии выбросов;
  • выделяет кластеры сложной формы и различных размеров,
  • обладает линейно зависимыми требованиями к месту хранения данных и временную сложность для данных высокой размерности.

Недостатки: есть необходимость в задании пороговых значений и количества кластеров.

Описание алгоритма :


Рисунок 1: Обзор CURE


Шаг 1: Построение дерева кластеров, состоящего из каждой строки входного набора данных.

Шаг 2: Формирование «кучи» в оперативной памяти, расчет расстояния до ближайшего кластера (строки данных) для каждого кластера. При формировании кучи кластеры сортируются по возрастанию дистанции от кластера до ближайшего кластера. Расстояние между кластерами определяется по двум ближайшим элементам из соседних кластеров. Для определения расстояния между кластерами используются «манхеттенская», «евклидова» метрики или похожие на них функции.

Шаг 3: Слияние ближних кластеров в один кластер. Новый кластер получает все точки входящих в него входных данных. Расчет расстояния до остальных кластеров для новообразованного кластера. Для расчета расстояния кластеры делятся на две группы: первая группа – кластеры, у которых ближайшими кластерами считаются кластеры, входящие в новообразованный кластер, остальные кластеры – вторая группа. И при этом для кластеров из первой группы, если расстояние до новообразованного кластера меньше чем до предыдущего ближайшего кластера, то ближайший кластер меняется на новообразованный кластер. В противном случае ищется новый ближайший кластер, но при этом не берутся кластеры, расстояния до которых больше, чем до новообразованного кластера. Для кластеров второй группы выполняется следующее: если расстояние до новообразованного кластера ближе, чем предыдущий ближайший кластер, то ближайший кластер меняется. В противном случае ничего не происходит.

Шаг 4: Переход на шаг 3, если не получено требуемое количество кластеров.

1.2 Математическое описание алгоритма

Прежде всего, алгоритм использует случайное разбиение выборки из [math] s [/math] элементов на [math] p [/math] частей, которые могут поместиться в память отдельной машины кластера. Затем во время первого прохода алгоритм уменьшает число кластеров в каждой подвыборке до [math] \frac{s}{pq} [/math], где [math] q \geq 1 [/math] – некоторая константа (происходит объединение ближайших кластеров). Для определения расстояния между кластерами используются «манхеттенская», «евклидова» метрики или похожие на них функции.

Метрика Евклида: [math]\rho(p,k) = \sqrt{\sum_{i=1}^n (p_{i} - k_{i})^2}[/math]

«Манхеттенская» метрика: [math]\rho(p,k) =\sum_{i=1}^n |p_{i} - k_{i}|[/math]

Если расстояние между ближайшей парой кластеров больше некоторого парогового(критического) значения, то объединения не происходит.

Для последующего шага на вход кластеризации подаются только представительные точки [math]c[/math] кластеров, полученных на предыдущем этапе. В ходе второго прохода алгоритма кластеризации остаются представительные точки для заданного количества кластеров. Алгоритм использует представительные точки, как метки, задающие форму и размер кластера.

Число точек представителей выбирается в зависимости от данных. Если возможно появление кластеров сложной формы, то точек должно быть больше, чтобы выявить их форму. В оригинальной статье авторы показывают что уже при [math]c[/math] равном [math]10[/math] достигается неплохая эффективность.

Рисунок 2: Результат работы алгоритка в зависимости от количесва представлений [math]c[/math].

Из рисунка видно, что при меньших значениях [math]c[/math] качество работы алгоритма ухудшается

Выбранные точки сдвигаются на [math]\alpha[/math] к центроиду кластера. Алгоритм становится основанным на методе поиска центроида при [math]\alpha = 1[/math], и основанным на всех точках кластера при [math]\alpha = 0[/math].

Рисунок 3: Чувствительность алгоритма к параметру [math]\alpha [/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное построение [math]k[/math] кластеров, вычисление их центроид и назначение точек-представителей.


1.4 Макроструктура алгоритма

Основную часть метода составляют разбиение случайной выборки строк на [math]k[/math] кластеров и нахождение точек-представителей для каждого кластера.

1.5 Схема реализации последовательного алгоритма

Входные параметры: набор входных данных [math]S[/math], содержащий [math]m[/math] точек в [math]n[/math]-мерном пространстве и требуемое количество кластеров [math]k[/math]. Начиная с отдельных точек в виде отдельных кластеров, на каждом шаге ближайшая пара кластеров объединяются, чтобы сформировать новый кластер.Процесс повторяется до тех пор, пока не достигнет [math]k[/math]. 

procedure cluster(S,k)
begin
1. T:=build_kd_tree(S)
2. Q:-build_heap(S)
3. while size(Q)>k do {
4.     u:=extract_min(Q)
5.     v:= u.closest
6.     delete(Q, V)
7.     w := merge(u,v) 
8.     delete_rep(T, u); delete_rep(T, v); insert_rep(T, w) 
9.     w.closest := x /* x is an arbitrary cluster in Q */
10.    for each x \in Qdo {
11.       if dist(w, x) < dist(w, w.closest) 
12.               w.closest := x 
13.       if x.closest is either u or w {  
14.             if dist(x, x.closest) < dist(x, w)
15.                 x.closest := closest_cluster(T, x, dist(x, w)) 
16.            else
17.               x.closest := w
18.             relocate(Q, x) 
19.        }
20.       else if dist(x, x.closest) > d&(x, w) { 
21.             x.closest := w 
22.             relocate(Q, x)
23.        }
24.      }
25.      insert(Q, w)
26. }
end

1.6 Последовательная сложность алгоритма

Являясь представителем иерархических алгоритмов кластеризации, имеет сложность [math] O(n^2 log(n)) [/math] и [math] O(n^2) [/math] для признаковых пространств малой размерности


1.7 Информационный граф

В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер.

Рисунок 4: Дендрограмма агломеративных методов

1.8 Ресурс параллелизма алгоритма

Т.к все действия алгорима (вычисления центроид для кластеров, расстояния между кластерами, представители кластеров и изменение положения представителей) на каждом шаге можно делать независимо (как от представителей данного кластера, так и представителей других кластеров), можно сделать вывод, что возможно распараллеливание

1.9 Входные и выходные данные алгоритма

Входные данные: набор данных [math] S [/math] , количество кластеров [math]k[/math], число точек представителей [math]c[/math], параметр [math]\alpha[/math], параметр [math]q[/math], [math]p[/math] число разбиений выборки, [math]n[/math] размерность.

Параметр [math]\alpha[/math] для сжатия точек представления к центру кластера.

Выходные данные: требуемое количество [math] k [/math] крастеров

1.9.1 Оптимальный выбор параметров для алгоритма

  • размер случайной выборки [math] S [/math] (а)

При запуске CURE со случайными размерами выборки в пределах от 500 до 5000 видно, что при размерах до 2000 были найдены кластеры низкого качества, начиная с 2500 точек и выше (2,5% от установленного размера данных), CURE всегда правильно определяет кластеры.

  • число точек представителей [math] c [/math] (b)

В оригинальной статье авторы показывают что уже при [math] c [/math] равном [math]10[/math] достигается неплохая эффективность.

  • число разбиений выборки [math] p [/math] (c)

[math] p [/math] должно быть выбрано таким, что [math] \frac{s}{pq} [/math] > [math] k [/math]

  • размерность (d)

CURE хорошо себя чувствует при больших размерностях

  • сжимающий фактор [math]\alpha[/math]

В оригинальной статье авторы показывают что [math]\alpha[/math] от 0.2 до 0.7 помогает хорошо выявлять несферические кластеры и подавлять редкие выбросы.

Рисунок 5: Влияние параметров [math] S [/math], [math] c [/math], [math] p [/math] и размерности на работу алгоритма.

1.10 Свойства алгоритма

  • является масштабируемым алгоритмом
  • неважна форма кластера и размер
  • работает только на числовых данных

2 ЧАСТЬ. Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

будет..

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Последовательная реализация CURE-алгоритма для кластеризации для Python/C++ представлена в пакете: pyclustering.

Также существует параллельная реализация алгоритма, описанная в сборнике [4]. Алгоритм предложенный в статье использует массив данных состоящий из размеров кластера, его центроида и репрезентативных точек, а при объединении кластеров информацию о новом кластере просто записывают в строчку предыдущего. Также для каждого кластера требуется считать индекс и расстояние до ближайшего кластера. Именно их поиск авторы статьи и предлагают распараллелить.

3 Литература

[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.

[2] Theodoridis, Sergios; Koutroumbas, Konstantinos (2006). Pattern recognition. Academic Press. pp. 572–574. ISBN 978-0-12-369531-4.

[3] Guha, Sudipto; Rastogi, Rajeev; Shim, Kyuseok (2001). "CURE: An Efficient Clustering Algorithm for Large Databases" (PDF). Information Systems. 26 (1): 35–58. doi:10.1016/S0306-4379(01)00008-4

[4] Panagiotis E. Hadjidoukas, Laurent Amsaleg. OpenMP Shared Memory Parallel Programming. Volume 4315 of the series Lecture Notes in Computer Science pp 289-299 Parallelization of a Hierarchical Data Clustering Algorithm Using OpenMP

Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Лукьянова_Анна/Алгоритм_кластеризации_с_использованием_представлений2&oldid=19478