Полный метод циклической редукции: различия между версиями
| [досмотренная версия] | [досмотренная версия] |
VadimVV (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 18: | Строка 18: | ||
{{Шаблон:Трёхдиагональная СЛАУ2}} | {{Шаблон:Трёхдиагональная СЛАУ2}} | ||
| − | '''Циклическая редукция''', как и все варианты прогонки, заключается <ref name="IK3d" | + | '''Циклическая редукция''', как и все варианты прогонки, заключается <ref name="IK3d" /><ref name="FAVT-2016">Фролов А.В., Антонов А.С., Воеводин Вл.В., Теплов А.М. Сопоставление разных методов решения одной задачи по методике проекта Algowiki // Параллельные вычислительные технологии (ПаВТ’2016): труды международной научной конференции (г. Архангельск, 28 марта – 1 апреля 2016 г.). Челябинск: Издательский центр ЮУрГУ, 2016. С. 347-360.</ref> в исключении из уравнений неизвестных, однако, в отличие от них, в ней исключение ведут одновременно по всей СЛАУ. В принципе, её можно считать вариантом [[Метод редукции|метода редукции]], выполняемого максимально возможное для данной СЛАУ число раз. |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 313: | Строка 313: | ||
Здесь необходимо отметить, что, несмотря на последовательность этой реализации, она вполне может быть исполнена и параллельно, нужно только как-то скомандовать имеющемуся в наличии компилятору, что циклы по i параллельны (например, спецкомментариями OpenMP). | Здесь необходимо отметить, что, несмотря на последовательность этой реализации, она вполне может быть исполнена и параллельно, нужно только как-то скомандовать имеющемуся в наличии компилятору, что циклы по i параллельны (например, спецкомментариями OpenMP). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| Строка 367: | Строка 318: | ||
Исходя из таких свойств алгоритма циклической редукции, как плохая локальность и наличие избыточности, логично было бы использовать его не в "чистом виде", а, проведя несколько этапов редукции, решать оставшуюся СЛАУ более простым методом вроде прогонки. | Исходя из таких свойств алгоритма циклической редукции, как плохая локальность и наличие избыточности, логично было бы использовать его не в "чистом виде", а, проведя несколько этапов редукции, решать оставшуюся СЛАУ более простым методом вроде прогонки. | ||
| − | + | Обычно циклическую редукцию как в блочном, так и в точечном варианте реализуют матфизики, решающие задачи с задачами, содержащими, например, дискретизацию оператора Лапласа. Её, несмотря на популярность, редко включают в пакеты программ. В основном это связано с тем, что простота схемы циклической редукции остаётся только для определённых размерностей задач, а универсальные решатели на её основе никто не делает. Для других размерностей могут быть придуманы разные, в том числе и более быстрые варианты циклической редукции<ref>А.В.Фролов "О коэффициенте при логарифме в критическом пути графа циклической редукции" // Суперкомпьютерные дни в России: Труды международной конференции (26-27 сентября 2016 г., г. Москва). – М.: Изд-во МГУ, 2016. с. 307-313.</ref>, но у них очень сложная схема, и каждый раз нужно выполнять анализ на устойчивость. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | В | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | === Результаты прогонов === |
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
В силу того, что граф алгоритма несколько схож по структуре на сдваивание, он лучше всего отображался бы на архитектуры типа гиперкуб, однако в последнее десятилетие стали ясны физические и технологические сложности для проектирования таких систем. Вместе с тем, его разработанность отдельными группами исследователей (в блочных вариантах, в том числе) вполне позволяет применять циклическую редукцию и на обычных массово параллельных компьютерах. Особенно рекомендуется не доводить циклическую редукцию до предела, а на отдельных узлах использовать такие старые методы, как монотонная и встречная прогонки. | В силу того, что граф алгоритма несколько схож по структуре на сдваивание, он лучше всего отображался бы на архитектуры типа гиперкуб, однако в последнее десятилетие стали ясны физические и технологические сложности для проектирования таких систем. Вместе с тем, его разработанность отдельными группами исследователей (в блочных вариантах, в том числе) вполне позволяет применять циклическую редукцию и на обычных массово параллельных компьютерах. Особенно рекомендуется не доводить циклическую редукцию до предела, а на отдельных узлах использовать такие старые методы, как монотонная и встречная прогонки. | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Литература == | == Литература == | ||
| Строка 407: | Строка 331: | ||
{{algorithm}} | {{algorithm}} | ||
[[Категория:Алгоритмы с избыточными вычислениями]] | [[Категория:Алгоритмы с избыточными вычислениями]] | ||
| + | |||
| + | [[Категория:Статьи в работе]] | ||
| + | |||
| + | [[en:Complete cyclic reduction]] | ||
Текущая версия на 14:10, 14 июля 2022
| Циклическая редукция для трёхдиагональной матрицы, точечный вариант | |
| Последовательный алгоритм | |
| Последовательная сложность | 17n + o(n) |
| Объём входных данных | 4n-2 |
| Объём выходных данных | n |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | 7 log_2 n |
| Ширина ярусно-параллельной формы | 3n/2 |
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Циклическая редукция - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ[1][2] вида Ax = b, где
- A = \begin{bmatrix} a_{11} & a_{12} & 0 & \cdots & \cdots & 0 \\ a_{21} & a_{22} & a_{23}& \cdots & \cdots & 0 \\ 0 & a_{32} & a_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & a_{n-1 n-2} & a_{n-1 n-1} & a_{n-1 n} \\ 0 & \cdots & \cdots & 0 & a_{n n-1} & a_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix}, b = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \\ \end{bmatrix}
Бывает, однако, что при изложении сути методов решения трёхдиагональных СЛАУ[3] элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид
- A = \begin{bmatrix} b_{1} & a_{1} & 0 & \cdots & \cdots & 0 \\ c_{2} & b_{2} & a_{2} & \cdots & \cdots & 0 \\ 0 & c_{3} & b_{3} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & c_{n-1} & b_{n-1} & a_{n-1} \\ 0 & \cdots & \cdots & 0 & c_{n} & b_{n} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix} = \begin{bmatrix} f_{1} \\ f_{2} \\ \vdots \\ f_{n} \\ \end{bmatrix}
или, если записывать отдельно по уравнениям, то
b_{1} x_{1} + a_{1} x_{2} = f_{1},
c_{i} x_{i-1} + b_{i} x_{i} + a_{i} x_{i+1} = f_{i}, 2 \le i \le n-1,
c_{n} x_{n-1} + b_{n} x_{n} = f_{n}.
Циклическая редукция, как и все варианты прогонки, заключается [3][4] в исключении из уравнений неизвестных, однако, в отличие от них, в ней исключение ведут одновременно по всей СЛАУ. В принципе, её можно считать вариантом метода редукции, выполняемого максимально возможное для данной СЛАУ число раз.
1.2 Математическое описание алгоритма
Лучше всего схема циклической редукции[3] разработана для случая n = 2^{m}-1. Эта схема состоит из прямого и обратного ходов. Прямой ход состоит из последовательного уменьшения в СЛАУ количества уравнений почти в 2 раза (за счёт подстановки из уравнений с нечётными номерами заменяются уравнения с чётными), пока не останется одно уравнение, обратный - в получении всё большего количества компонент решения исходной СЛАУ. Оба хода - как прямой, так и обратный - разбиты на шаги. Здесь мы приведём тот вариант алгоритма, в котором операции экономятся за счёт предварительной нормировки уравнений, используемых для исключения неизвестных.
1.2.1 Прямой ход редукции
В начале считается, что все c^{(0)}_{i} = c_{i}, b^{(0)}_{i} = b_{i}, a^{(0)}_{i} = a_{i}, f^{(0)}_{i} = f_{i}, x^{(0)}_{i} = x_{i}
На k-м шаге теперь выполняем процедуру редукции системы уравнений размерности n.
Для каждого из уравнений
c^{(k)}_{i} x^{(k)}_{i-1} + b^{(k)}_{i} x^{(k)}_{i} + a^{(k)}_{i} x^{(k)}_{i+1} = f^{(k)}_{i}
с нечётными i с помощью деления уравнения на b^{(k)}_{i} выполняется его замена на уравнение
(c^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i-1} + x^{(k)}_{i} + (a^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i+1} = f^{(k)}_{i}/b^{(k)}_{i}
Уравнение
b^{(k)}_{1} x^{(k)}_{1} + a^{(k)}_{1} x^{(k)}_{2} = f^{(k)}_{1}
аналогично меняется на уравнение
x^{(k)}_{1} + (a^{(k)}_{1}/b^{(k)}_{1}) x^{(k)}_{2} = f^{(k)}_{1}/b^{(k)}_{1}:
а уравнение
c^{(k)}_{n} x^{(k)}_{n-1} + b^{(k)}_{n} x^{(k)}_{n} = f^{(k)}_{n}
меняется на уравнение
(c^{(k)}_{n}/b^{(k)}_{n}) x^{(k)}_{n-1} + x^{(k)}_{n} = f^{(k)}_{n}/b^{(k)}_{n}:
Для каждого же из уравнений
c^{(k)}_{i} x^{(k)}_{i-1} + b^{(k)}_{i} x^{(k)}_{i} + a^{(k)}_{i} x^{(k)}_{i+1} = f^{(k)}_{i}
с чётными i (кроме 2 и n-2) выполняется, с учётом x^{(k+1)}_{i/2} = x^{(k)}_{i} его замена на уравнение
c^{(k+1)}_{i/2} x^{(k+1)}_{(i-2)/2} + b^{(k+1)}_{i/2} x^{(k+1)}_{i/2} + a^{(k+1)}_{i/2} x^{(k+1)}_{(i+2)/2} = f^{(k+1)}_{i/2}
при этом
c^{(k+1)}_{i/2} = - c^{(k)}_{i}(c^{(k)}_{i-1}/b^{(k)}_{i-1}),
a^{(k+1)}_{i/2} = - a^{(k)}_{i}(a^{(k)}_{i+1}/b^{(k)}_{i+1}),
b^{(k+1)}_{i/2} = b^{(k)}_{i} - c^{(k)}_{i}(a^{(k)}_{i-1}/b^{(k)}_{i-1}) - a^{(k)}_{i}(c^{(k)}_{i+1}/b^{(k)}_{i+1}),
f^{(k+1)}_{i/2} = f^{(k)}_{i} - c^{(k)}_{i}f^{(k)}_{i-1}/b^{(k)}_{i-1} - a^{(k)}_{i}f^{(k)}_{i-1}/b^{(k)}_{i-1}.
Для 2го уравнения выполняется его замена на уравнение
b^{(k+1)}_{1} x^{(k+1)}_{1} + a^{(k+1)}_{1} x^{(k+1)}_{(2} = f^{(k+1)}_{1}
при этом
a^{(k+1)}_{1} = - a^{(k)}_{2}(a^{(k)}_{3}/b^{(k)}_{3}),
b^{(k+1)}_{1} = b^{(k)}_{2} - c^{(k)}_{2}(a^{(k)}_{1}/b^{(k)}_{1}) - a^{(k)}_{2}(c^{(k)}_{3}/b^{(k)}_{3}),
f^{(k+1)}_{1} = f^{(k)}_{2} - c^{(k)}_{2}f^{(k)}_{1}/b^{(k)}_{1} - a^{(k)}_{2}f^{(k)}_{1}/b^{(k)}_{1}
n-1-е уравнение заменяется на
c^{(k+1)}_{(n-1)/2} x^{(k+1)}_{(n-3)/2} + b^{(k+1)}_{(n-1)/2} x^{(k+1)}_{(n-1)/2} = f^{(k+1)}_{(n-1)/2}
при этом
c^{(k+1)}_{(n-1)/2} = - c^{(k)}_{n-1}(c^{(k)}_{n-2}/b^{(k)}_{n-2}),
b^{(k+1)}_{(n-1)/2} = b^{(k)}_{n-1} - c^{(k)}_{n-1}(a^{(k)}_{n-2}/b^{(k)}_{n-2}) - a^{(k)}_{n-1}(c^{(k)}_{n}/b^{(k)}_{n}),
f^{(k+1)}_{(n-1)/2} = f^{(k)}_{n-1} - c^{(k)}_{n-1}f^{(k)}_{n-2}/b^{(k)}_{n-2} - a^{(k)}_{n-1}f^{(k)}_{n-2}/b^{(k)}_{n-2}.
По окончании всех этих манипуляций размерность k+1-й СЛАУ оказывается равной (n-1)/2.
Шаги повторяются до тех пор, пока после m-1 шагов редукции размерность СЛАУ не становится равной 1 и остаётся одно уравнение
b^{(m-1)}_{1} x^{(m-1)}_{1} = f^{(m-1)}_{1}
1.2.2 Обратный ход редукции
Из последнего уравнения, полученного прямым ходом, вычисляется
x^{(m-1)}_{1} = f^{(m-1)}_{1}/b^{(m-1)}_{1}
Теперь, последовательно уменьшая верхние индексы неизвестных, используется нечётные уравнения каждого шага для вычисления неизвестных с соотвествующими нечётными номерами. Чётные неизвестные получаются из тождеств x^{(k)}_{i} = x^{(k+1)}_{i/2}, а для нечётных i
x^{(k)}_{i} = f^{(k)}_{i}/b^{(k)}_{i} - (c^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i-1} - (a^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i+1}
c "левого края" системы будет
x^{(k)}_{1} = f^{(k)}_{1}/b^{(k)}_{1} - (a^{(k)}_{1}/b^{(k)}_{1}) x^{(k)}_{2}
а с "правого"
x^{(k)}_{n} = f^{(k)}_{n}/b^{(k)}_{n} - (c^{(k)}_{n}/b^{(k)}_{n}) x^{(k)}_{n-1}
После вычисления всех x^{(0)}_{i} значения искомых неизвестных x_{i} = x^{(k)}_{i}.
1.3 Вычислительное ядро алгоритма
Видно, что, поскольку вычисляемые на каждом шаге прямого хода редукции при преобразовании нечётных уравнений отношения коэффициентов
c^{(k)}_{i}/b^{(k)}_{i} , a^{(k)}_{i}/b^{(k)}_{i} , f^{(k)}_{i}/b^{(k)}_{i}
почти все используются для преобразований двух чётных уравнений, то при выделении "микровычислений", из которых следует составить шаги редукции и которые составляют его ядро, лучше отнести вычисления этих отношений к предыдущему шагу редукции. Таким образом, на "подготовительном шаге" микроядро будет для каждого нечётного i состоять только из трёх делений (кроме 2 и n - там будет по 2 деления), а затем на каждом последующем шаге редукции для каждого нечётного i - из двух умножений и двух вычислений выражений типа a-bc-de, с последующими тремя делениями (на "краях" часть этих операций отсутствует или урезана, но общую картину это не очень меняет). Для чётных i деления в микроядре будут отсутствовать.
Что касается шагов обратного хода, то там для каждого i рано или поздно выполняется одна операция типа a-bc-de (на "краях" - типа a-bc).
1.4 Макроструктура алгоритма
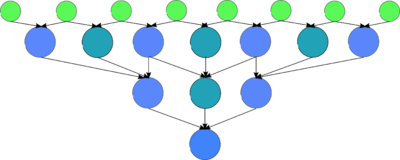
Если выразить макроструктуру алгоритма циклической редукции в терминах её "микроядер", то прямой ход редукции несколько схож на схемы сдваивания, но отличается от неё не только количеством входящих в макровершины дуг, из-за чего её схема - скорее "страивание", но и зацеплением соседних ветвей. Поэтому, в отличие от схем сдваивания, для которых характерно полностью независимое исполнение ветвей до определённого момента, в схеме редукции это зацепление ветвей не даёт им выполняться полностью независимо.
Обратный ход циклической редукции - уже практически полное "обратное" сдваивание, и на этом этапе разделение на независимые ветви может быть проделано после старта, если размножить необходимые данные.
1.5 Схема реализации последовательного алгоритма
Метод циклической редукции изначально спроектирован для параллельного исполнения, поскольку является по отношению к, например, классической прогонке, алгоритмом с избыточными вычислениями. Поэтому смысла в его последовательной реализации обычно не видят и они не встречаются в библиотеках программ. Тем не менее, из-за того, что современная архитектура даже одиночных узлов и персональных компьютеров не вполне последовательна, то этот смысл, как вполне может оказаться[4], уже появился, поскольку, кроме простого количества операций, производительность вычислений на компьютере определяется и другими параметрами алгоритма, в частности, локальностью вычислений.
1.6 Последовательная сложность алгоритма
Поскольку алгоритм циклической редукции обычно не предназначен для последовательного исполнения, то его "последовательную сложность" скорее следует считать только оценкой общего количества операций. Если взять только главный член, линейный по размеру, и опустить меньшие по порядку (логарифмические и константы), то получается, что в циклической редукции 3n делений, 8n умножений и 6n вычитаний/сложений. Таким образом, при классификации по последовательной сложности, алгоритм циклической редукции относится к алгоритмам с линейной сложностью.
Сравнение сложности с алгоритмом прогонки показывает также, что циклическая редукция - алгоритм с избыточными вычислениями: избыточность по сравнению с прогонкой более чем в 2 раза.
1.7 Информационный граф
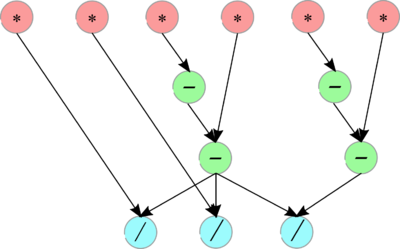
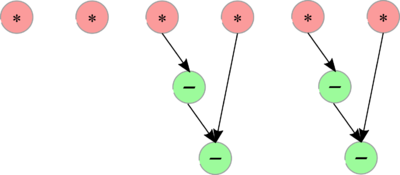
У прямого хода циклической редукции макрограф представлен на Рис. 4, при этом графы разные макровершин представлены на Рис. 1, 2a, 2b. Как видно, после первого шага схему можно условно назвать "схемой страивания", поскольку связанные с каждым уравнением, остающимся в редуцированной СЛАУ, коэффициенты вычисляются по формулам из коэффициентов трёх соседних уравнений в нередуцированной СЛАУ.
Обратный ход имеет макрограф, представленный на Рис. 5, при этом графы макровершин представлены на Рис. 3 (крайние макровершины, имеющие только одну входящую дугу на макрографе, замещают недостающие данные нулями, соответственно уменьшая вычисления). Этот макрограф, в принципе, имеет макроструктуру, обратную к схеме сдваивания, поэтому её можно условно назвать "схемой раздваивания", с одной поправкой: все макровершины, кроме крайних, имеют по две входящих дуги, которые немного изменяют обычное "раздваивание".
1.8 Ресурс параллелизма алгоритма
Для выполнения циклической редукции в трёхдиагональной СЛАУ из n уравнений с n неизвестными в параллельном варианте требуется последовательно выполнить следующие ярусы:
- log_2 n ярусов делений, из них самый широкий ярус - первый, в нём 3n/2 делений.
- 2 log_2 n ярусов умножений и 4 log_2 nсложений/вычитаний.
Ширина ярусов экспоненциально, с показателем 2, убывает с их номерами, а потом, на обратном ходе, экспоненциально растёт, также с показателем 2. Эта неоднородность приводит к тому, что при практическом полном распараллеливании большую часть времени большинство устройств будет простаивать.
Таким образом, при классификации по высоте ЯПФ, прогонка относится к алгоритмам с логарифмической сложностью. При классификации по ширине ЯПФ её сложность будет линейной.
1.9 Входные и выходные данные алгоритма
Входные данные: трёхдиагональная матрица A (элементы a_{ij}), вектор b (элементы b_{i}).
Объём входных данных: 4n-2.
Выходные данные: вектор x (элементы x_{i}).
Объём выходных данных: n.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности, как хорошо видно, является отношением размера задачи к его логарифму.
При этом вычислительная мощность алгоритма как отношение числа операций к суммарному объему входных и выходных данных является константой.
Алгоритм в рамках выбранной версии полностью детерминирован.
Обычно циклическая редукция используется для решения СЛАУ с диагональным преобладанием. В этом случае гарантируется устойчивость алгоритма.
В случае, когда требуется решение нескольких СЛАУ с одной и той же матрицей, большую часть прямого хода вычислений (см. рисунки с графом алгоритма) можно не повторять.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
Из-за избыточности вычислений на компьютерах без параллельных устройств обычно используют более простую монотонную или встречную прогонку, а циклическую редукцию в последовательном варианте обычно просто не реализуют. Этот выбор, однако, не так очевиден на современных "однопроцессорных" суперскалярных компьютерах, поскольку в циклической редукции нет такой избыточной локальности, как в прогонке. Однако, эта сторона циклической редукции ещё не исследована и ждёт тех, кто проведёт соответствующую работу.
Приведем пример подпрограммы, реализующей циклическую прогонку СЛАУ с числом уравнений "степень двойки минус 1", где все элементы матрицы хранятся в одном массиве, причём соседние элементы матричной строки размещаются рядом, а вычисляемые коэффициенты - на месте уже ненужных элементов исходной матрицы. Следует обратить внимание на то, что данная версия циклической редукции непригодна для повторного решения СЛАУ с той же матрицей и новой правой частью, поскольку при повторении нужно несколько большее количество промежуточных данных.
subroutine cprogm (a,x,N,m) ! N=2^m-1
real a(3,N), x(N)
k=1
k2=2
kk=1
a(2,1)=1./a(2,1)
a(2,N)=1./a(2,N)
a(3,1)=a(3,1)*a(2,1)
a(1,N)=a(1,N)*a(2,N)
x(1) = x(1)*a(2,1)
x(N) = x(N)*a(2,N)
do i=3,N-2,2
a(2,i) = 1./a(2,i)
a(1,i) = a(1,i)*a(2,i)
a(3,i) = a(3,i)*a(2,i)
x(i) = x(i)*a(2,i)
end do
do j=1,m-2
k=k2 ! k=2^j
a(2,k) = a(2,k) - a(1,k)*a(3,k-kk)
a(3,k) = -a(3,k)*a(3,k+kk)
x(k) = x(k)- x(k-kk)*a(1,k-kk)
a(2,N+1-k) = a(2,N+1-k) - a(1,N+1-k)*a(3,N+1-k-kk)
a(1,N+1-k)= - a(1,N+1-k)*a(1,N+1-k-kk)
x(N+1-k) = x(N+1-k)- x(N+1-k-kk)*a(1,N+1-k-kk)
a(2,k) = a(2,k) - a(3,k)*a(1,k+kk)
x(k) = x(k) - x(k+kk)*a(3,k+kk)
a(2,N+1-k) = a(2,N+1-k) - a(3,N+1-k)*a(1,N+1-k+kk)
x(N+1-k) = x(N+1-k)- x(N+1-k+kk)*a(3,N+1-k+kk)
k2=k2*2 ! k2=2^(j+1)
do i = k2, N+1-k2, k
a(2,i) = a(2,i) - a(1,i)*a(3,i-kk)
x(i) = x(i)- x(i-kk)*a(1,i-kk)
a(3,i) = -a(3,i)*a(3,i+kk)
a(1,i)= - a(1,i)*a(1,i-kk)
a(2,i) = a(2,i) - a(3,i)*a(1,i+kk)
x(i) = x(i)- x(i+kk)*a(3,i+kk)
end do
a(2,k)=1./a(2,k)
a(2,N+1-k)=1./a(2,N+1-k)
a(3,k)=a(3,k)*a(2,k)
a(1,N+1-k)=a(1,N+1-k)*a(2,N+1-k)
x(k) = x(k)*a(2,k)
x(N+1-k) = x(N+1-k)*a(2,N+1-k)
do i = k2+k, N+1-k2-k, k2
a(2,i) = 1./a(2,i)
a(1,i) = a(1,i)*a(2,i)
a(3,i) = a(3,i)*a(2,i)
x(i) = x(i)*a(2,i)
end do
kk=k ! budet kk=2^(j-1)
end do
c m-1 shag & start of reverse
k=k2 ! k=2^(m-1) i kk=2^(m-2)
a(2,k) = a(2,k) - a(1,k)*a(3,k-kk)
x(k) = x(k)- x(k-kk)*a(1,k-kk)
a(2,k) = a(2,k) - a(3,k)*a(1,k+kk)
x(k) = x(k)- x(k+kk)*a(3,k+kk)
a(2,k) = 1./a(2,k)
x(k) = x(k)*a(2,k)
c start reverse
x(kk) = x(kk) - a(3,kk)*x(k)
x(k+kk) = x(k+kk) - a(1,k+kk)*x(k)
do j=m-2, 1, -1
k2 = k ! k2 = 2^(j+1)
k = kk ! k = 2^j
kk = kk/2 ! kk = 2^(j-1)
x (kk) = x (kk) - a(3,kk)*x(kk+kk)
x (N+1-kk) = x (N+1-kk) - a(1,N+1-kk)*x(N+1-k)
do i = k2+k, N+1-k-kk, k2
x(i) = x(i) - a(1,i)*x(i-kk)
end do
do i = k2+k, N+1-k-kk, k2
x(i) = x(i) - a(3,i)*x(i+kk)
end do
end do
return
end
Здесь необходимо отметить, что, несмотря на последовательность этой реализации, она вполне может быть исполнена и параллельно, нужно только как-то скомандовать имеющемуся в наличии компилятору, что циклы по i параллельны (например, спецкомментариями OpenMP).
2.2 Возможные способы и особенности параллельной реализации алгоритма
Исходя из таких свойств алгоритма циклической редукции, как плохая локальность и наличие избыточности, логично было бы использовать его не в "чистом виде", а, проведя несколько этапов редукции, решать оставшуюся СЛАУ более простым методом вроде прогонки.
Обычно циклическую редукцию как в блочном, так и в точечном варианте реализуют матфизики, решающие задачи с задачами, содержащими, например, дискретизацию оператора Лапласа. Её, несмотря на популярность, редко включают в пакеты программ. В основном это связано с тем, что простота схемы циклической редукции остаётся только для определённых размерностей задач, а универсальные решатели на её основе никто не делает. Для других размерностей могут быть придуманы разные, в том числе и более быстрые варианты циклической редукции[5], но у них очень сложная схема, и каждый раз нужно выполнять анализ на устойчивость.
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
В силу того, что граф алгоритма несколько схож по структуре на сдваивание, он лучше всего отображался бы на архитектуры типа гиперкуб, однако в последнее десятилетие стали ясны физические и технологические сложности для проектирования таких систем. Вместе с тем, его разработанность отдельными группами исследователей (в блочных вариантах, в том числе) вполне позволяет применять циклическую редукцию и на обычных массово параллельных компьютерах. Особенно рекомендуется не доводить циклическую редукцию до предела, а на отдельных узлах использовать такие старые методы, как монотонная и встречная прогонки.
3 Литература
- ↑ Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.
- ↑ Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.
- ↑ Перейти обратно: 3,0 3,1 3,2 Ильин В.П., Кузнецов Ю.И. Трехдиагональные матрицы и их приложения. М.: Наука. Глав-ная редакция физико-математической литературы, 1985г., 208 с.
- ↑ Перейти обратно: 4,0 4,1 Фролов А.В., Антонов А.С., Воеводин Вл.В., Теплов А.М. Сопоставление разных методов решения одной задачи по методике проекта Algowiki // Параллельные вычислительные технологии (ПаВТ’2016): труды международной научной конференции (г. Архангельск, 28 марта – 1 апреля 2016 г.). Челябинск: Издательский центр ЮУрГУ, 2016. С. 347-360.
- ↑ А.В.Фролов "О коэффициенте при логарифме в критическом пути графа циклической редукции" // Суперкомпьютерные дни в России: Труды международной конференции (26-27 сентября 2016 г., г. Москва). – М.: Изд-во МГУ, 2016. с. 307-313.